基于集成算法的路段短時(shí)行駛時(shí)間預(yù)測(cè)

蔣怡玥，董蜀黔，周淑敏

(1.北京交通大學(xué)交通運(yùn)輸學(xué)院，北京 100044；2.北京郵電大學(xué)信息與通信工程學(xué)院，北京 100876)

路段行駛時(shí)間是反映道路擁擠程度最為直觀的參數(shù)[1]，是構(gòu)建交通信息服務(wù)系統(tǒng)、交通流誘導(dǎo)系統(tǒng)等ITS子系統(tǒng)的重要基礎(chǔ)。從道路管理者和出行者的角度來(lái)看，了解道路交通狀況并對(duì)其進(jìn)行短時(shí)預(yù)測(cè)，在運(yùn)輸效率和可靠性方面都是值得關(guān)注的問(wèn)題。不僅可以輔助管理者應(yīng)對(duì)交通擁堵和實(shí)施應(yīng)急策略，還可以幫助出行者規(guī)劃自己的行程和路線，以避開(kāi)擁擠的路段，避免旅行延誤。時(shí)間尺度越小，實(shí)時(shí)性越好，越能真實(shí)反映路段的交通狀態(tài)；但正是如此，路段行駛時(shí)間常呈現(xiàn)出強(qiáng)烈的波動(dòng)，而這些快速變化往往是復(fù)雜且難以預(yù)測(cè)的。因此，基于交通信息建立算法模型，精準(zhǔn)預(yù)測(cè)各路段在某個(gè)時(shí)段的通行時(shí)間，對(duì)交通狀態(tài)波動(dòng)進(jìn)行預(yù)測(cè)，有助于城市交通智能管控和社會(huì)智慧出行，是現(xiàn)在交通發(fā)展的大勢(shì)所趨。

行駛時(shí)間預(yù)測(cè)對(duì)于交通預(yù)測(cè)來(lái)說(shuō)一直是一個(gè)重要的研究領(lǐng)域，國(guó)內(nèi)外學(xué)者已經(jīng)將很多方法用于其中。由于交通狀態(tài)的動(dòng)態(tài)性和非線性，短時(shí)旅行時(shí)間的預(yù)測(cè)仍是一個(gè)非常有挑戰(zhàn)性的任務(wù)。現(xiàn)有的應(yīng)用于短時(shí)行駛時(shí)間預(yù)測(cè)的數(shù)據(jù)驅(qū)動(dòng)方法可分為兩大類，即參數(shù)方法和非參數(shù)方法。

參數(shù)方法主要有線性回歸模型[2]、時(shí)間序列模型，如卡爾曼濾波[3]、自回歸綜合移動(dòng)平均法[4]。在這些模型中，交通狀態(tài)本質(zhì)上假定為線性的。當(dāng)交通呈現(xiàn)有規(guī)律的變化時(shí)可以產(chǎn)生比較理想的預(yù)測(cè)結(jié)果，而對(duì)于波動(dòng)性較強(qiáng)和非線性的交通狀態(tài)，這些方法計(jì)算耗時(shí)并且易產(chǎn)生較大的偏差。由于非參數(shù)方法對(duì)基本模型不做很強(qiáng)的假設(shè)，應(yīng)用中相對(duì)具有優(yōu)勢(shì)[5]。其中，以神經(jīng)網(wǎng)絡(luò)為代表的方法對(duì)非線性關(guān)系的擬合能力使得其在交通預(yù)測(cè)方面得到了廣泛應(yīng)用[6]。神經(jīng)網(wǎng)絡(luò)算法具有較強(qiáng)的魯棒性和容錯(cuò)能力，但是神經(jīng)網(wǎng)絡(luò)缺乏解釋性，且對(duì)參數(shù)比較敏感，需要比較多的參數(shù)訓(xùn)練，訓(xùn)練時(shí)間過(guò)長(zhǎng)，可能預(yù)測(cè)結(jié)果更差。

近年來(lái)，在解決預(yù)測(cè)問(wèn)題方面，基于集成的算法被應(yīng)用于各個(gè)領(lǐng)域并取得了巨大的成功[7]。在各種不同的集成方法中，基于樹(shù)的集成方法是一種流行的集成方法，該方法將多個(gè)簡(jiǎn)單樹(shù)模型結(jié)合，優(yōu)化預(yù)測(cè)性能。基于樹(shù)的集成模型的可解釋性使得交通決策者能夠更好地理解模型的輸出，并且便于分析交通量之間的影響因素。這些特性使得基于樹(shù)的集成方法在解決交通問(wèn)題方面具有很好的應(yīng)用前景。Hamner[8]將隨機(jī)森林(random forest，RF)應(yīng)用于旅行時(shí)間預(yù)測(cè)中并在IEEE ICDM比賽中表現(xiàn)最佳，相比于其他算法具有明顯優(yōu)勢(shì)。梯度提升樹(shù)(gradient boosting decision tree，GBDT)與傳統(tǒng)的統(tǒng)計(jì)方法和其他集成方法相比，在預(yù)測(cè)精度方面具有優(yōu)越的性能。Zhang等[9]首次將梯度提升樹(shù)應(yīng)用于旅行時(shí)間預(yù)測(cè)，并得到了很好的結(jié)果，尤其是在交通狀況發(fā)生突變時(shí)。

盡管在高速公路交通預(yù)測(cè)方面已經(jīng)做了大量工作，但其中基于樹(shù)的集成方法在短時(shí)交通預(yù)測(cè)中應(yīng)用十分有限。路段行駛時(shí)間隨時(shí)間的變化波動(dòng)很大，而天氣、節(jié)假日等非線性因素都會(huì)對(duì)路段行駛時(shí)間造成影響，時(shí)間尺度較小時(shí)，其不確定性和時(shí)變性較強(qiáng)[10]。基于樹(shù)的集成方法得到的結(jié)果可解釋性較強(qiáng)，不僅能夠處理不同類型的預(yù)測(cè)變量，并且可以較好地?cái)M合復(fù)雜的非線性關(guān)系，可直接通過(guò)原始數(shù)據(jù)預(yù)測(cè)路段行駛時(shí)間，因此更加適合路段行駛時(shí)間的短時(shí)預(yù)測(cè)。在機(jī)器學(xué)習(xí)中，基于樹(shù)的集成方法通常比傳統(tǒng)的統(tǒng)計(jì)方法具有更好的預(yù)測(cè)性能。本文提出了一個(gè)基于樹(shù)的集成方法來(lái)預(yù)測(cè)短時(shí)的路段行駛時(shí)間。首先針對(duì)小時(shí)間尺度下交通時(shí)變性強(qiáng)這一特性，通過(guò)對(duì)其損失函數(shù)的改造得到一個(gè)更加魯棒的GBDT，并與RF進(jìn)行融合。其次考慮各種歷史旅行時(shí)間數(shù)據(jù)的相關(guān)變量，以揭示影響旅行時(shí)間波動(dòng)的重要因素。最后，比較了不同方法的預(yù)測(cè)準(zhǔn)確性及算法穩(wěn)定性。

1 數(shù)據(jù)分析

1.1 數(shù)據(jù)描述

本文數(shù)據(jù)來(lái)源于天池大數(shù)據(jù)競(jìng)賽中智慧交通預(yù)測(cè)挑戰(zhàn)賽。數(shù)據(jù)集中記錄了城市關(guān)鍵路段的屬性信息、路段間網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)，以及歷史每天以2 min為一個(gè)間隔的每條路段上的平均旅行時(shí)間。提供2017年4月至2017年6月132條路段以2 min為一個(gè)時(shí)間窗的覆蓋全天的旅行時(shí)間數(shù)據(jù)。

1.2 數(shù)據(jù)處理

缺失值利用歷史相同時(shí)間片的行駛時(shí)間進(jìn)行補(bǔ)充。由于均值可能受到統(tǒng)計(jì)樣本中極端值的影響，因此本文使用數(shù)據(jù)集中觀察到的路段旅行時(shí)間的中位數(shù)進(jìn)行缺失數(shù)據(jù)填充，具體缺失數(shù)據(jù)填充流程見(jiàn)圖1。

1.3 特征工程

表1是本文所選取數(shù)據(jù)集特征的一個(gè)示例，其中in_tt和out_tt分別表示車輛經(jīng)過(guò)與該路段相鄰的上、下游路段的行駛時(shí)間；length，width分別表示該路段的路段屬性(長(zhǎng)、寬)；of_day表示車輛通過(guò)該路段的不同時(shí)間段；of_week的索引從1到7代表從星期一到星期日；pretime表示與上一個(gè)時(shí)間段車輛經(jīng)過(guò)該路段的行駛時(shí)間，t2-t1表示連續(xù)兩個(gè)時(shí)間段的行駛時(shí)間變化率；最后將天氣(weather)也作為考慮因素加入特征中。

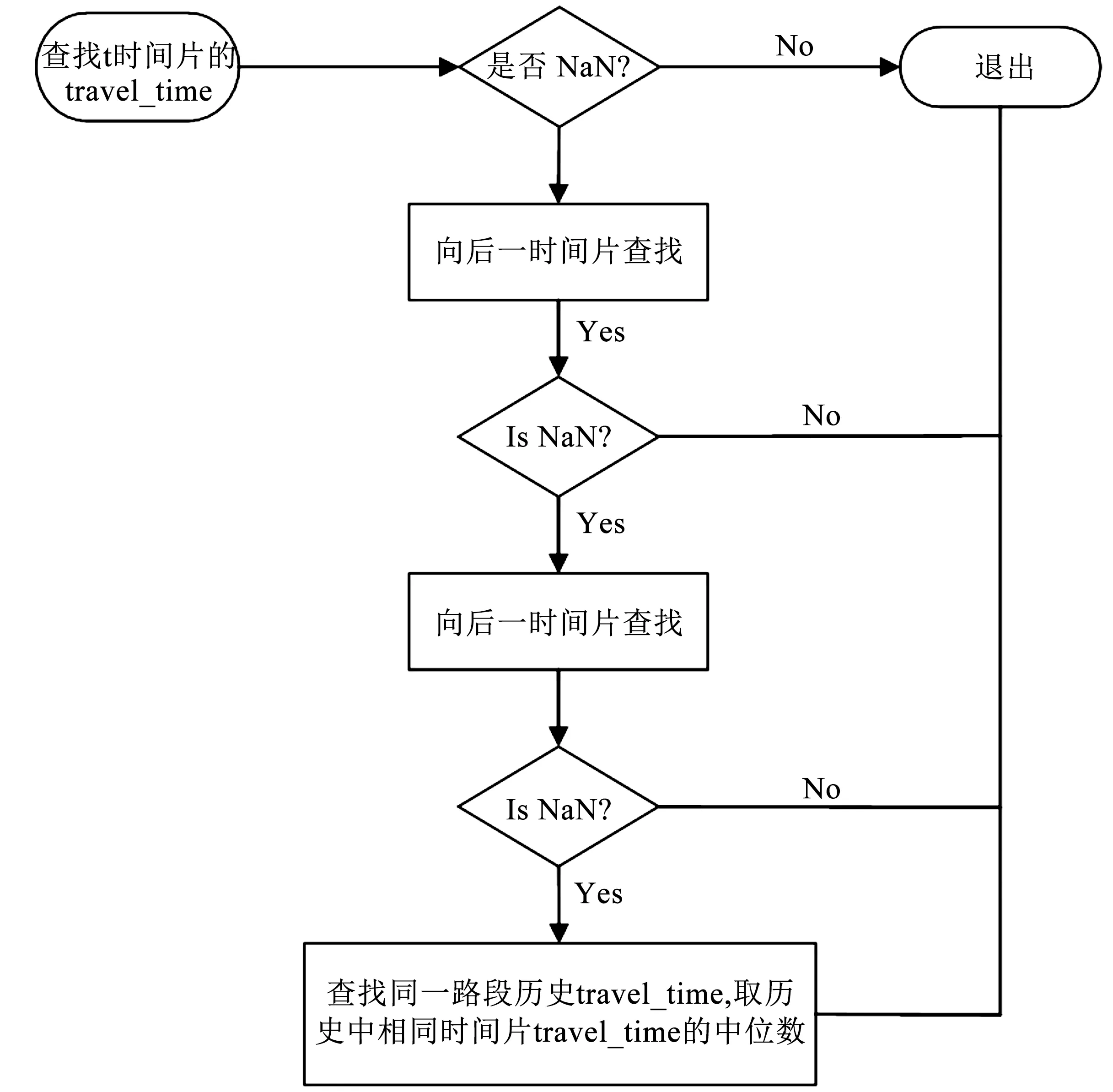
圖1 缺失數(shù)據(jù)填充流程圖Fig.1 The process of filling the missing data

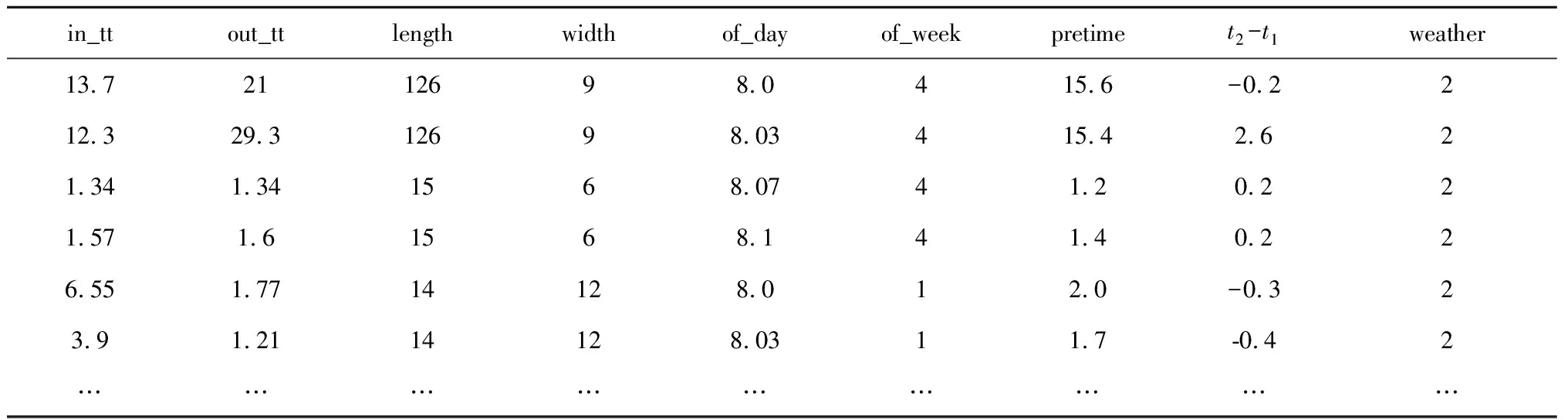
表1 數(shù)據(jù)集實(shí)例Table 1 Example of the data set

2 理論方法

2.1 隨機(jī)森林(RF)法

Breiman等[11]結(jié)合Boostrap重采樣技術(shù)和Random Subspace Method提出RF，RF是由多個(gè)決策樹(shù)構(gòu)成的森林。決策樹(shù)在生成的過(guò)程中首先分別在行方向和列方向上添加隨機(jī)過(guò)程，行方向上構(gòu)建決策樹(shù)時(shí)采用自助抽樣得到訓(xùn)練數(shù)據(jù)，列方向上采用無(wú)放回隨機(jī)抽樣得到特征子集，并據(jù)此得到其最優(yōu)切分點(diǎn)；之后就是對(duì)采樣之后的數(shù)據(jù)使用完全分裂的方式建立出決策樹(shù)；每棵決策樹(shù)都最大可能地進(jìn)行生長(zhǎng)而不進(jìn)行剪枝(由于之前的兩個(gè)隨機(jī)采樣的過(guò)程保證了隨機(jī)性，所以就算不剪枝，也不會(huì)出現(xiàn)過(guò)擬合)；最后通過(guò)對(duì)所有的決策樹(shù)進(jìn)行加總來(lái)預(yù)測(cè)新的數(shù)據(jù)。

2.2 梯度提升樹(shù)法(GBDT)

梯度提升的觀點(diǎn)是基于Boosting算法提出的一個(gè)改進(jìn)[12]。假設(shè)yi,i=1,2,…,n代表i時(shí)刻某路段實(shí)際行駛時(shí)間的觀測(cè)值，迭代輪數(shù)為t=1,2,…,T，則ft-1(xi)表示第t-1輪i時(shí)刻路段行駛時(shí)間的預(yù)測(cè)值。Freidman[13]提出了用損失函數(shù)的負(fù)梯度來(lái)擬合本輪損失的近似值，進(jìn)而擬合一個(gè)回歸樹(shù)。其中，第t輪的i時(shí)刻的損失函數(shù)的負(fù)梯度表示為：

。

(1)

因此GBDT的目標(biāo)是，找到損失函數(shù)是L(·)使本輪損失最小：

(2)

Freidman[13]將損失函數(shù)定義為：

。

(3)

則可以求得第t輪的i時(shí)刻損失函數(shù)的負(fù)梯度：

。

(4)

也就是說(shuō)GBDT中的梯度方向?qū)?yīng)于i時(shí)刻某路段行駛時(shí)間的觀測(cè)值與預(yù)測(cè)值之差，即“殘差”，由此可以看出GBDT每一輪產(chǎn)生的殘差作為下一輪回歸樹(shù)的輸入，下一輪的回歸樹(shù)的目的就是盡可能地?cái)M合這個(gè)輸入的殘差。

2.3 魯棒的GBDT

GBDT通過(guò)在每一輪梯度方向上減少殘差，以提高模型性能。而在過(guò)程中容易受到突變點(diǎn)的影響，對(duì)突變點(diǎn)就會(huì)很敏感，因此對(duì)于小時(shí)間尺度下劇烈波動(dòng)的交通狀況，可能會(huì)表現(xiàn)不佳。本文針對(duì)這一問(wèn)題，選擇了不同的損失函數(shù)，以抑制突變點(diǎn)的影響，得到更加穩(wěn)健的GBDT。

(5)

令損失函數(shù)L(·)為：

(6)

其中，變量w表示觀察值與預(yù)測(cè)值之差，即殘差；m為參數(shù)。

這個(gè)函數(shù)表示對(duì)于殘差w值較小的點(diǎn)，其損失函數(shù)是二次的，而對(duì)于w值較大的點(diǎn)其損失函數(shù)是線性的，這種方法有助于減少突變點(diǎn)對(duì)交通預(yù)測(cè)的影響。

2.4 RF-GBDT回歸

偏差(Bias)度量了學(xué)習(xí)算法的期望預(yù)測(cè)與真實(shí)結(jié)果的偏離程度；方差(Variance)度量了同樣大小訓(xùn)練集的變動(dòng)所導(dǎo)致的學(xué)習(xí)性能的變化。泛化性能是由偏差和方差共同決定的，從圖2刻畫的泛化誤差與偏差、方差的關(guān)系，可以看出，偏差與方差之間是存在沖突的，即當(dāng)學(xué)習(xí)器擬合能力不夠強(qiáng)時(shí)，訓(xùn)練數(shù)據(jù)的擾動(dòng)不足以使學(xué)習(xí)器產(chǎn)生顯著變化，此時(shí)偏差主導(dǎo)泛化錯(cuò)誤率；而當(dāng)學(xué)習(xí)器的擬合能力足夠強(qiáng)時(shí)，訓(xùn)練數(shù)據(jù)的輕微擾動(dòng)會(huì)導(dǎo)致學(xué)習(xí)器發(fā)生顯著變化，此時(shí)方差主導(dǎo)泛化錯(cuò)誤率。這就是所謂的偏差-方差窘境。

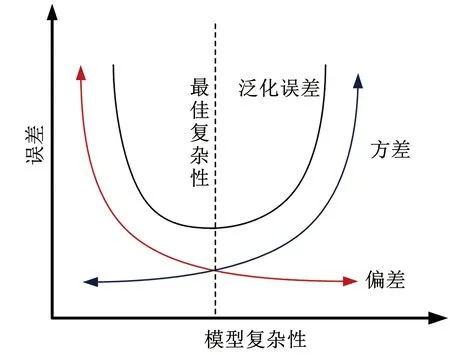
圖2 泛化誤差與偏差、方差的關(guān)系示意圖Fig.5 The relationship between total error and bias, variance

從前文的分析發(fā)現(xiàn)對(duì)于RF，其核心就是自采樣(樣本隨機(jī))和屬性隨機(jī)，屬于樣本數(shù)相同下的不同訓(xùn)練集產(chǎn)生的預(yù)測(cè)結(jié)果，即數(shù)據(jù)的擾動(dòng)導(dǎo)致模型學(xué)習(xí)性能的變化，因此RF主要關(guān)注降低方差提高模型性能；而對(duì)于GBDT，其核心是擬合損失函數(shù)梯度，而損失函數(shù)的定義就決定了在子區(qū)域內(nèi)各個(gè)步長(zhǎng)，其中就是期望輸出與預(yù)測(cè)輸出的差，因此GBDT主要關(guān)注降低偏差提高模型性能。另外，當(dāng)樹(shù)的數(shù)量足夠多時(shí)，RF不會(huì)產(chǎn)生過(guò)擬合，提高樹(shù)的數(shù)量能夠使得錯(cuò)誤率降低；而GBDT的每棵樹(shù)是按順序生成的，每棵樹(shù)生成時(shí)都需要利用之前一棵樹(shù)留下的信息，樹(shù)的數(shù)目過(guò)多時(shí)會(huì)引起過(guò)擬合。

因此，本文考慮在進(jìn)行預(yù)測(cè)時(shí)，將RF與魯棒的GBDT進(jìn)行結(jié)合，彼此優(yōu)勢(shì)互補(bǔ)，使得新的模型能夠克服過(guò)擬合現(xiàn)象，同時(shí)兼顧偏差-方差，以產(chǎn)生更好的效果。在本文中，將RF和魯棒的GBDT進(jìn)行融合得到RF-GBDT，并將其應(yīng)用到路段行駛時(shí)間預(yù)測(cè)中。RF-GBDT算法過(guò)程如下。

輸入：訓(xùn)練集D={(x1,y1),(x2,y2),…,(xm,ym)};

初級(jí)學(xué)習(xí)算法：RF;

次級(jí)學(xué)習(xí)算法：GBDT.

過(guò)程：

h=RF(D);

D'=φ;

for i=1,2,…,m do

zi=h(xi);

D'=D'∪(zi,yi);

end for

h'=GBDT(D');

輸出：H(x)=h'(h(x)).

圖3是生成RF-GBDT并進(jìn)行預(yù)測(cè)的具體流程。值得一提的是，在訓(xùn)練階段，GBDT的訓(xùn)練集是利用RF產(chǎn)生的，若直接使用，過(guò)擬合的風(fēng)險(xiǎn)較大，因此本文使用交叉驗(yàn)證法，用RF未使用的樣本來(lái)產(chǎn)生GBDT的訓(xùn)練樣本。

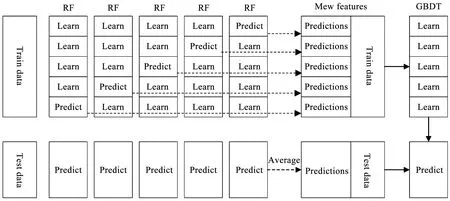
圖3 RF-GBDT流程示意圖Fig.3 The process of RF-GBDT

具體步驟如下：

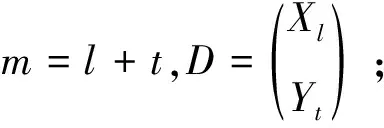
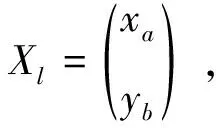
3 結(jié)果

3.1 評(píng)價(jià)指標(biāo)

評(píng)價(jià)指標(biāo)采用平均絕對(duì)百分誤差(mean absolute percent error，MAPE)，計(jì)算公式如下：

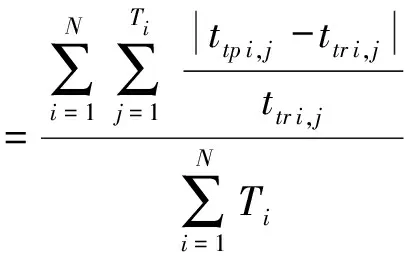
(7)

其中：ttp：預(yù)測(cè)的行駛時(shí)間；ttr：真實(shí)的行駛時(shí)間；N：預(yù)測(cè)路段數(shù)量；Ti：第i個(gè)路段上的預(yù)測(cè)時(shí)間片數(shù)量；MAPE值越低說(shuō)明模型準(zhǔn)確度越高。

3.2 變量解釋

為了檢測(cè)本文所提算法的精度和穩(wěn)定性，利用已知數(shù)據(jù)對(duì)2017年7月早高峰8:00—9:00、日平峰15:00—16:00和晚高峰18:00—19:00 三個(gè)時(shí)段中各一個(gè)小時(shí)的數(shù)據(jù)(以2 min為粒度)進(jìn)行短時(shí)預(yù)測(cè)。根據(jù)處理之后的數(shù)據(jù)，分別使用RF、GBDG、RF-GBDT進(jìn)行預(yù)測(cè)。其中，在使用RF-GBDT進(jìn)行預(yù)測(cè)時(shí)，一般來(lái)說(shuō)，k值越大其穩(wěn)定性和保真性越好，但是效率也會(huì)隨之減少；經(jīng)過(guò)測(cè)試，k=5時(shí)，可同時(shí)滿足穩(wěn)定性和效率要求。

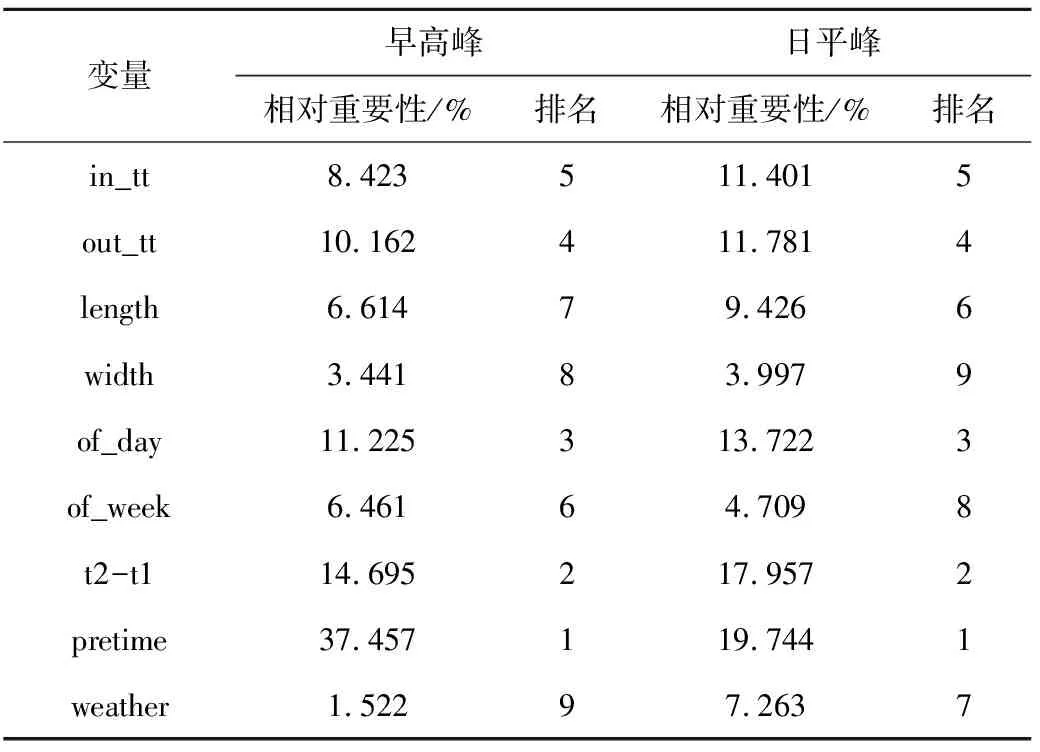
表2 輸入變量對(duì)預(yù)測(cè)結(jié)果的相對(duì)影響Table 2 Relative influence of input variables on prediction

表2給出了每個(gè)輸入變量對(duì)模型輸出的相對(duì)影響。很明顯，每個(gè)輸入變量對(duì)模型的輸出有不同的貢獻(xiàn)。在兩個(gè)情況下，上一個(gè)時(shí)間段車輛經(jīng)過(guò)該路段的行駛時(shí)間pretime對(duì)于行駛時(shí)間的預(yù)測(cè)貢獻(xiàn)最大，事實(shí)也是如此，路段上一時(shí)間段的交通狀況影響之后的交通，與未來(lái)的行駛時(shí)間密切相關(guān)。行駛時(shí)間變化率t2-t1對(duì)模型輸出也有較大的影響，其表示了交通的變化，其中一個(gè)正的t2-t1值，表示行駛時(shí)間具有增加的趨勢(shì)，t2-t1值與交通擁擠正相關(guān)。我們可以看出，車輛在相鄰路段的行駛時(shí)間也很大程度影響該路段的行駛時(shí)間；另外相比于早高峰，路段本身的屬性在日平峰對(duì)行駛時(shí)間的影響有所提升，這與日平峰道路交通狀況良好有關(guān)；而天氣對(duì)早高峰的作用很微弱，這是因?yàn)樵绺叻宄鲂械闹饕康臑橥ㄇ凇?/p>

3.3 預(yù)測(cè)結(jié)果

根據(jù)預(yù)測(cè)結(jié)果輸出MAPE值并繪制三個(gè)時(shí)段不同預(yù)測(cè)周期不同方法下的MAPE對(duì)比圖。圖4代表7月份上半月早高峰、日平峰和晚高峰的MAPE值。從圖中我們可以看出，總的來(lái)說(shuō)，RF的預(yù)測(cè)效果不如GBDT，特別是在早晚高峰交通狀況變化劇烈時(shí)，GBDT尤其好于RF，這從側(cè)面反應(yīng)了GBDT的魯棒性較好，能夠較好地反映交通的劇烈變化；而在早晚高峰和日平峰兩種交通狀態(tài)下，RF-GBDT的預(yù)測(cè)效果均為最佳，特別是在交通狀況變化劇烈時(shí)。圖5表示7月1日—7月15日及7月1日—7月31日三個(gè)時(shí)段平均MAPE值。從圖中不難看出，RF-GBDT的預(yù)測(cè)效果明顯好于RF和GBDT。而預(yù)測(cè)周期增加之后，MAPE隨之增大，精度有所下降，也就是說(shuō)預(yù)測(cè)周期越長(zhǎng)，越難以捕捉復(fù)雜的交通狀況；對(duì)于RF-GBDT，雖然其MAPE有所上升，但上升幅度最小。從預(yù)測(cè)周期和交通狀況兩個(gè)方面的預(yù)測(cè)結(jié)果，RF-GBDT在精度和穩(wěn)定性上都優(yōu)于單獨(dú)的RF或GBDT。

圖4 7月1日—7月15日分時(shí)段輸出MAPE對(duì)比圖Fig.4 The comparison of three periods’ MAPE from July 1st to 15th

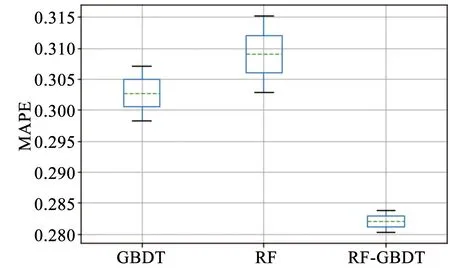
圖5 7月1日—7月15日與7月1日—7月31日三個(gè)時(shí)段平均MAPE對(duì)比圖Fig.5 The comparison of average MAPE from July 1st to 15th and July 1st to July 31st

4 結(jié)語(yǔ)

本文以2 min為預(yù)測(cè)時(shí)間尺度，以實(shí)際路段行駛時(shí)間為基礎(chǔ)，將在回歸預(yù)測(cè)領(lǐng)域表現(xiàn)良好，并且效率較高的兩個(gè)以RF和GBDT為代表的基于樹(shù)的集成學(xué)習(xí)方法，應(yīng)用到路段行駛時(shí)間的短時(shí)預(yù)測(cè)中。為了使GBDT能夠較好地反映劇烈變化的交通情況，對(duì)其損失函數(shù)進(jìn)行了處理。在偏差-方差方面，為了提高模型性能，RF主要關(guān)注降低方差；而對(duì)于GBDT，其主要關(guān)注降低偏差。因此，提出一種改進(jìn)的RF-GBDT算法。

在對(duì)路段行駛時(shí)間進(jìn)行短時(shí)預(yù)測(cè)的過(guò)程中，考慮了天氣對(duì)交通的影響。本文分別使用RF、GBDT、RF-GBDT對(duì)比不同預(yù)測(cè)周期、不同交通狀況下輸出的MAPE值，并對(duì)變量進(jìn)行解釋。實(shí)驗(yàn)結(jié)果表明，RF-GBDT能夠有效應(yīng)對(duì)交通狀況劇烈變化并進(jìn)行預(yù)測(cè)，無(wú)論是在精度還是在算法穩(wěn)定性方面，RF-GBDT都表現(xiàn)出了優(yōu)越性。

本文所提方法在對(duì)短時(shí)的路段行駛時(shí)間進(jìn)行預(yù)測(cè)時(shí)，雖然預(yù)測(cè)結(jié)果得到了改進(jìn)，但是在進(jìn)行方法融合的過(guò)程中，其計(jì)算成本也會(huì)隨之增加，日后可以從這個(gè)方面進(jìn)行提升。