非整平自由設(shè)站在軌道快速測量中的應(yīng)用

馬文靜

(中鐵工程設(shè)計咨詢集團有限公司，北京 100055)

1 概述

不論是有砟軌道高速鐵路還是無砟軌道高速鐵路，均需要進行軌道測量及軌道精調(diào)，使建成軌道的平順性滿足高速行車的要求[1-3]。傳統(tǒng)的軌道測量方法是將全站儀架設(shè)在腳架上并精確整平，然后基于線路兩側(cè)的軌道控制網(wǎng)(CPⅢ)進行自由設(shè)站測量[4-7]，在設(shè)站精度滿足規(guī)范要求之后，才能開始軌道測量工作。這種方法的弊端在于每次搬站后均需要對全站儀進行精確整平，不僅花費時間較多，降低工作效率，而且對測量人員的操作技能要求也比較高。在運營高速鐵路普遍采用“天窗修”[8]的線路養(yǎng)護模式下，這種作業(yè)效率較低的軌道測量方法已不適應(yīng)現(xiàn)實的需要。

為了提高軌道測量作業(yè)的工作效率，一個可行的方法是去掉全站儀精確整平的操作流程，同時也不再進行人工搬站。提出一種將全站儀架設(shè)在軌檢小車上，與之保持剛性連接的新型軌道測量裝備，其結(jié)構(gòu)如圖1所示。在開展軌道測量工作時，全站儀與軌檢小車一同移動，當(dāng)需要進行自由設(shè)站測量時，則將軌檢小車停下并進行自由設(shè)站測量工作。這種軌道測量新方法，由于沒有了搬站及精確整平的過程，節(jié)省了大量的時間，將使軌道測量效率較之傳統(tǒng)方法成倍提升。

圖1 全站儀與軌檢小車連接結(jié)構(gòu)示意

全站儀架設(shè)在軌檢小車上并進行自由設(shè)站時，其狀態(tài)是非整平的。通過觀測一定數(shù)量且三維坐標已知的CPⅢ控制點，解算全站儀的站心三維坐標，從而對軌檢小車當(dāng)前所處的位置進行準確定位。軌道線路在曲線段存在超高，在線路縱向上存在縱坡，以及由于施工、運營等原因造成的各種軌道不平順，使得全站儀的非整平狀態(tài)較為復(fù)雜，必須建立一種通用、準確的站心三維坐標解算數(shù)學(xué)模型，使之能夠適用于各種非整平狀態(tài)，并保證站心三維坐標的解算精度。

2 站心三維坐標解算的理論模型

全站儀在非整平狀態(tài)下觀測CPⅢ控制點，其實質(zhì)是建立了一個以站心為坐標原點、任意定向且Z軸不與水平面垂直的空間直角坐標系，所有的觀測值均處于這個坐標系之下；另一方面，已知三維坐標的CPⅢ控制網(wǎng)在本質(zhì)上是一個Z軸垂直于水平面的空間直角坐標系。兩個空間直角坐標系之間的軸系關(guān)系，可以采用歐拉角分解為三次繞軸轉(zhuǎn)動，并利用方向余弦矩陣聯(lián)系起來。

設(shè)繞Z，X，Y軸依次旋轉(zhuǎn)的角度分別為θ、φ及γ，平移參數(shù)分別為ΔX、ΔY、ΔZ，尺度比為μ，原坐標系下用(x、y、z)表示點坐標，新坐標系下用(u、v、w)表示點坐標，則兩個空間直角坐標系間的轉(zhuǎn)換關(guān)系見式(1)[9]

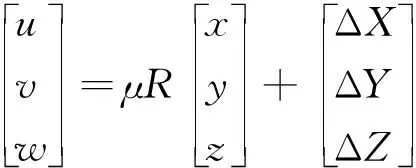
(1)

式(1)為非線性方程組，包含三個旋轉(zhuǎn)角、三個平移量及一個尺度因子，一共7個未知數(shù)，在最少已知三個公共點的情況下即可求解。R為基于三個歐拉旋轉(zhuǎn)角組成的3階方向余弦矩陣[10]，如式(2)所示。該3階矩陣的9個元素之間相互不獨立，而且直接以角度為未知數(shù)還存在象限判斷的問題，在對方程進行線性化時會存在較大的精度損失，難以保證解算成果的準確性，需要尋求一種高精度且實用的計算方法。

(2)

3 站心三維坐標的實用算法

3.1 羅德里格矩陣

定義反對稱矩陣S

(3)

式(3)中a、b、c為三個相互獨立的未知數(shù)，則方向余弦矩陣R可由S構(gòu)成的羅德里格矩陣[11-13]表示為

R=(I+S)(I-S)-1

(4)

式(4)中I為3階單位矩陣。如此構(gòu)建的矩陣R中的各元素間相互獨立，不僅便于開列線性化法方程，也便于未知數(shù)的初值求解。

3.2 七參數(shù)初值求解

設(shè)有三個公共點，則可首先根據(jù)邊長之比計算尺度因子，有

(5)

將式(4)代入式(1)，利用點1及點2的坐標開列方程，并相互作差消去三個平移參數(shù)并整理[6]，有

(6)

式(6)為關(guān)于未知數(shù)a、b、c的三個線性方程組，由于只含有兩個獨立方程，不能解算三個未知數(shù)，需再利用點1及點3開列方程組，聯(lián)立求得未知數(shù)a、b、c，然后利用式(4)計算得到R矩陣，最后根據(jù)式(7)計算兩個空間直角坐標系之間的平移參數(shù)。

(7)

3.3 最小二乘法求解模型

在全站儀非整平自由設(shè)站中，通常會觀測6～8個CPⅢ控制點，對所有點按照式(1)開列方程求解七參數(shù)時會存在多余觀測，需要采用最小二乘法平差求解最或然概率下的結(jié)果。首先可通過上述七參數(shù)初值計算方法，任意選擇3個點求解七參數(shù)初值。由于從6～8個點中任選3個點存在多種選法，可計算出多組七參數(shù)初值。考慮到CPⅢ控制點位移導(dǎo)致的坐標不準確、點位網(wǎng)形強度等因素，并確保最小二乘平差計算中能夠迭代收斂，七參數(shù)初值特別是方向余弦矩陣初值應(yīng)該具有較好的精度，可按照式(8)選擇L2范數(shù)定義下值最小的一組。

(8)

初值求解完成后，將式(3)代入式(4)，經(jīng)整理得到以a、b、c表示的方向余弦矩陣R，再將R代入式(1)并整理，有

(9)

對式(9)進行線性化，按照最小二乘法開列誤差方程并求解[14-15]

(10)

3.4 站心坐標計算及精度估計

全站儀非整平狀態(tài)下自身空間直角坐標系的原點就是其站心，三軸坐標值均為零；基于式(1)，解算得到的三個平移參數(shù)ΔX、ΔY、ΔZ就是站心在CPⅢ坐標系下的坐標。利用式(1)計算經(jīng)坐標變換后的CPⅢ控制點坐標，并與已知坐標進行比較，利用式(11)計算各個控制點每個坐標軸向的坐標殘差

(11)

(12)

式(12)中，n為非整平自由設(shè)站時所觀測的CPⅢ控制點個數(shù)，站心坐標的坐標殘差可由式(11)所計算的每個CPⅢ控制點坐標殘差的平均值來估計。按照誤差傳播定律，站心坐標在三個軸向的坐標中誤差可根據(jù)式(13)估算

(13)

4 實測數(shù)據(jù)分析

為驗證該方法在全站儀各種非整平狀態(tài)下的通用性及計算的準確性，在某無砟高速鐵路上進行了非整平自由設(shè)站試驗。試驗在線路左線開展，每120 m進行一次非整平自由設(shè)站測量，每次設(shè)站觀測8個CPⅢ控制點，站與站之間搭接4個CPⅢ控制點。試驗區(qū)段總長約12 km，包含2條右偏曲線，1條左偏曲線，圓曲線半徑分別為14 000 m、9 000 m、14 000 m，設(shè)計超高分別為75 mm、120 mm、85 mm。試驗共計進行124次非整平自由設(shè)站測量，每次設(shè)站測量時，全站儀在線路橫向及縱向與水平面之間的角度如圖2所示。

圖2 全站儀非整平狀態(tài)下與水平面的傾角

由圖2可見，對全站儀非整平狀態(tài)進行線路橫向及縱向分解，得到這兩個方向全站儀與水平面之間的傾角。在線路橫向，由于受曲線超高的影響，傾角變化的幅度較大；以右偏曲線傾角為負值，左偏曲線傾角為正值，則直線地段的傾角約為0°；75 mm，120 mm及85 mm曲線超高地段的傾角分別約為-2.8°、4.6°及-3.2°，緩和曲線地段的傾角則是從直線到圓曲線之間的平緩過渡。線路縱向坡度一般不會太大，以上坡傾角為正值，下坡傾角為負值，則本試驗段在縱向的傾角變化范圍約為-0.2°～0.2°。由上述分析可知，本次試驗的124次非整平自由設(shè)站測量包含了各種軌道測量工況下的非整平狀態(tài)，具有較好的代表性。

非整平自由設(shè)站下站心坐標解算完成后，利用式(13)計算各CPⅢ控制點的坐標殘差，通過對每一站所觀測6～8個CPⅢ控制點三個坐標分量的殘差進行分析，可以對CPⅢ控制點的穩(wěn)定性進行評價。對于變形明顯及移動的CPⅢ點，則將其剔除，使其不參與站心三維坐標的解算過程，從而達到控制測量精度的目的。表1所示為某次非整平自由設(shè)站所觀測的7個CPⅢ控制點全部參與解算后所得的坐標殘差情況，點057325、057327、057329及057331的高程殘差均較大，其中點057329的高程殘差最大，且該點東坐標、北坐標的殘差分別為-30.37 mm，-22.16 mm，也是所有點當(dāng)中最大的，因此可以判定點057329大概率發(fā)生了變形，不應(yīng)參與數(shù)據(jù)解算，應(yīng)當(dāng)做粗差剔除；在未剔除粗差的情況下，計算得到的站心三維坐標的東、北、高為494 550.463 5 m，4 376 136.655 1 m，15.342 4 m，對應(yīng)的坐標中誤差為4.77 mm，3.44 mm，20.52 mm，表明所得的站心三維坐標精度很差，不能滿足使用要求。

表1 粗差剔除前的CPⅢ控制點坐標分量殘差 mm

由于該站共觀測了7個CPⅢ控制點，具有足夠的多余觀測，因此可將點057329當(dāng)做粗差剔除。對剩余的6個CPⅢ控制點數(shù)據(jù)重新計算，得到的坐標殘差見表2所示，可見每個點在三個坐標分量上的殘差均小于2 mm，說明這6個CPⅢ點的兼容性較好，精度均勻。解算所得的站心三維坐標為494 550.467 6 m、4 376 136.658 0 m、15.308 7 m，對應(yīng)的坐標中誤差為0.32 mm、0.24 mm、0.30 mm，表明解算結(jié)果達到了較高的精度。與未剔除點057329之前的計算結(jié)果相比，坐標中誤差大幅度縮小且均小于0.7 mm，站心三維坐標的變化量為-4.1 mm、-2.9 mm、33.7 mm，進一步說明了點057329不僅造成了站心坐標中誤差偏大，同時也使站心三維坐標產(chǎn)生了較大的偏差。

表2 粗差剔除后的CPⅢ控制點坐標分量殘差 mm

按照上述方法對所有124站數(shù)據(jù)進行處理，并保證每一站至少有5個點參與站心三維坐標解算，所得CPⅢ控制點坐標殘差的分布情況如圖3所示。經(jīng)統(tǒng)計，東坐標殘差絕對值大于2 mm的比例為0.5%，北坐標殘差絕對值大于2 mm的比例為0.7%，高程殘差絕對值大于2 mm的比例為0.7%。坐標殘差分布表明，本次非整平自由設(shè)站試驗所采用的CPⅢ控制點整體精度良好。

圖3 CPⅢ控制點殘差分布

如圖4所示，在東坐標、北坐標及高程三個軸向上，站心坐標的中誤差均未超過0.7 mm。

圖4 站心坐標中誤差分布

《高速鐵路工程測量規(guī)范》(TB10601—2009)要求在全站儀整平自由設(shè)站的前提下，站心坐標三個軸向中誤差應(yīng)小于0.7 mm，坐標殘差應(yīng)小于2 mm，由此可見，在CPⅢ控制網(wǎng)精度良好的情況下，進行全站儀非整平自由設(shè)站并采用該方法解算站心三維坐標、站心坐標中誤差及CPⅢ控制點坐標殘差等成果，達到了整平自由設(shè)站所要求的各項指標精度。

5 結(jié)束語

利用全站儀非整平自由設(shè)站的方法，可以省去傳統(tǒng)軌道測量方法中對全站儀搬站及精確整平的工作過程，不僅大幅度提高了軌道測量的作業(yè)效率，而且降低了對作業(yè)人員的技能要求，具有巨大的技術(shù)優(yōu)勢。采用該方法的關(guān)鍵環(huán)節(jié)在于準確可靠地解算站心三維坐標，并給出相應(yīng)的精度評定指標。鑒于此，給出了非整平自由設(shè)站下站心三維坐標解算的理論模型及實用算法，并利用運營高速鐵路高精度的CPⅢ控制網(wǎng)進行了124站各種線路狀況下的非整平自由設(shè)站測量試驗。測試結(jié)果表明，該方法能夠適應(yīng)軌道測量過程中的各種傾斜狀態(tài)下的數(shù)據(jù)解算，根據(jù)控制點坐標殘差能夠發(fā)現(xiàn)并剔除粗差點， 99%的CPⅢ控制點坐標殘差均小于2 mm，站心坐標東、北、高程三個方向的中誤差均小于0.7 mm，計算結(jié)果準確可靠，滿足相關(guān)規(guī)范標準，達到了軌道測量對作業(yè)精度的要求。