鐵道工程中兩種常用GNSS高程 擬合方法的比較研究

余 騰 胡伍生 吳 杰 孫小榮 趙升峰

(1.宿遷學院建筑工程學院，江蘇宿遷 223800；2.東南大學交通學院，江蘇南京 210096； 3.南京市測繪勘察研究院有限公司，江蘇南京 210019)

近年來，伴隨GNSS(Global Navigation Satellite System)技術的快速發展和廣泛應用，在鐵道沿線建立GNSS帶狀控制網已成常態。借用GNSS控制點與道路沿線部分水準點重合，采用GNSS技術獲取道路沿線一定數量控制點的高程數據，并利用其幾何水準測量高程資料，選擇科學的數學方法進行擬合計算并對精度進行分析[1-2]。

GNSS測量得到的高程是以WGS-84參考橢球為基準的大地高，而實際工程中使用的是以似大地水準面為基準的正常高，同一點位兩個數值的差值即為高程異常值ξ；如何選擇合適的函數模型對數據進行擬合，求得每個點的高程異常值，進而準確地將大地高轉化成正常高是研究者關注的重點，也是實現精確的GNSS高程擬合的關鍵[3-6]。

1 高程系統基礎理論

1.1 水準面基本概念

在大地測量與工程測量中，通常會涉及水準面、大地水準面、似大地水準面幾個概念[7]。

水準面是基于地球自轉的慣性離心力和地球引力交叉產生的重力作用而形成的一個處處與重力方向垂直的連續曲面，也是一個重力等位面。

大地水準面是一個與平均海水面重合并延伸到大陸內部形成的水準面。因地表起伏和地球內部質量分布不勻，故大地水準面是一個略有起伏的不規則曲面。該面包圍的形體近似于一個旋轉橢球，稱為“大地體”，大地水準面是最接近地球整體形狀的重力位水準面，也是正高系統的高程基準面。

似大地水準面是從地面點沿正常重力線量取正常高所得端點構成的封閉幾何曲面。由于正高與大地水準面的確定涉及到地球內部密度的假定，在理論上存在著不嚴密性，為了便于計算，原蘇聯專家莫洛金斯基提出似大地水準面，可以應用地面測量數據直接確定地球表面形狀而不需要對地球密度作任何假設。似大地水準面接近于水準面，沒有物理意義，只是一個輔助面。

1.2 主要高程系統

(1)大地高是地面點沿參考橢球面法線到參考橢球面的距離，它克服了難以獲得地球內部準確質量數據的困難，各個區域建立自己的參考橢球也有助于獲得本區域較高精度的高程值。地球上任意位置處的大地高指沿經由待測點的旋轉球體的法線到旋轉體之間的長度。大地高沒有實際意義，只是數學層面上的定義。GNSS測量得到的高程是以WGS-84參考橢球為基準的大地高[8]。在WGS-84世界大地坐標系下，地表P點的大地高用Hp表示(如圖1)。

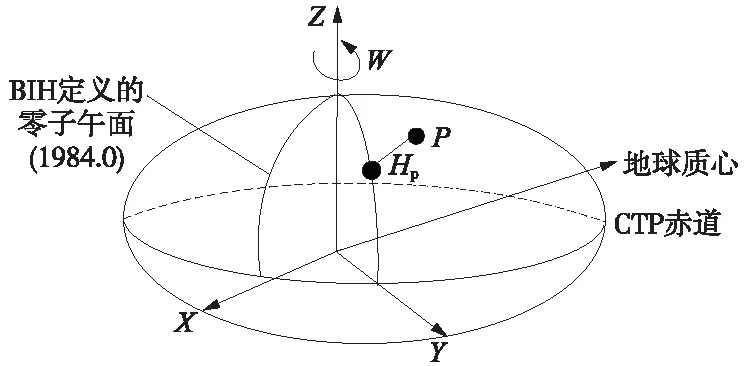
圖1 WGS-84 世界大地坐標系與大地高

(2)正高系統是以大地水準面為基準面的高程系統。可表示為

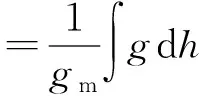
(1)

其中gm是點沿垂線到相應基準面間的平均重力值，dh是該方向上的高差，因為gm和該未知點所處地方的密度和深度有關，其密度深度數據難以精確測量[9]，因此，正高不能準確得到，把大地水準面與橢球面間的距離用N表示，有關系式

N=H-H正

(2)

(3)正高雖有完整的物理意義，鑒于每個區域的引力常數無法準確測得，正高并不能準確得到，為了便于計算研究，人們提出正常高系統。公式記為

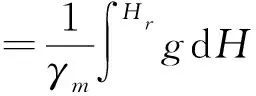
(3)

式中，γm為平均正常重力值，則地表某點到大地水準面和似大地水準面間距離差為

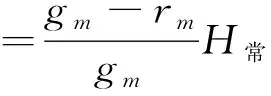
(4)

式中，gm-rm為重力異常，似大地水準面和參考橢球兩個基準之間距離叫做高程異常，記為ξ

ξ=H-H常

(5)

總體來說，幾種主要高程系統關系可用圖2示意。

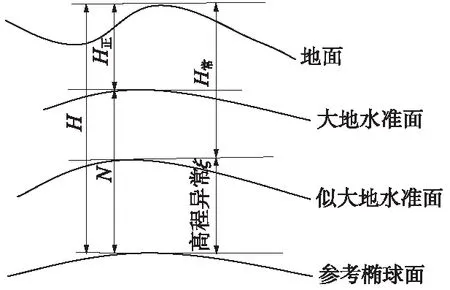
圖2 高程系統關系示意

2 GNSS高程擬合原理

直接獲取測區內GNSS點的大地高后，選擇若干數量和位置均能滿足高程擬合要求的GNSS點，通過水準測量方法對GNSS點進行水準聯測或在水準點上布設GNSS點，獲取其正常高數據，計算點位的高程異常，選擇模型算法進行高程擬合計算，求得測區內其他GNSS點的正常高[10]。

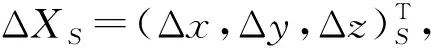
先對GNSS觀測基線向量進行解算，把坐標作為未知參數進行自由網平差，求出其三維地心坐標，再在網中選取不少于3個聯測控制點(控制點經度、緯度、大地高數據已知)。將這些點轉到相應橢球的三維坐標中，有

(6)

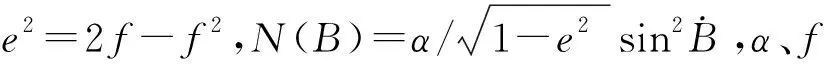
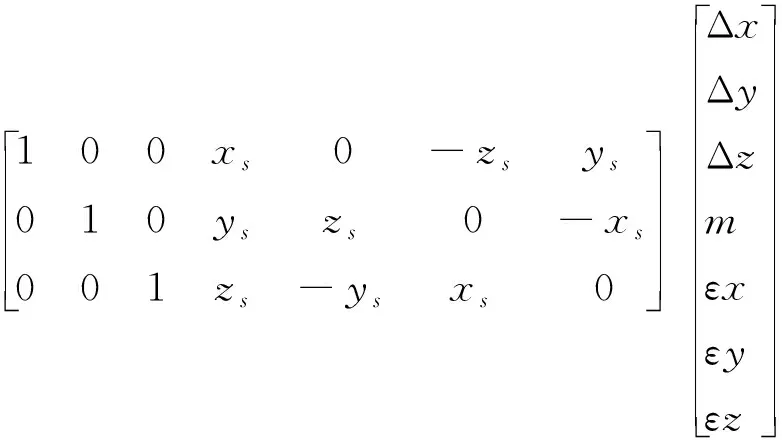
(7)

式中，Δx，Δy，Δz為平移參數，m是尺度比，εx，εy，εz為旋轉參數。求得GNSS控制點相應坐標系下的直角坐標，再經過如下變換

L=arctan(y/x)

(8)

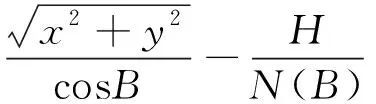
(9)

可得到與已知控制點同一參考橢球下的經緯度和大地高數據。在進行坐標系轉換時多采用7參數或4參數法，GNSS網點經過轉換后和地面點間仍存在間隙，可在編制軟件過程中采取了一些措施來消除部分不兼容情況[12]。

3 GNSS高程擬合方法與精度評定

3.1 適用于道路工程的GNSS高程擬合方法選取

根據數據獲取和處理方法不同，GNSS高程可分為：GNSS三角高程、GNSS重力高程、GNSS水準高程[13]。GNSS三角高程是利用已知的GNSS點高程數據，測出各點之間的豎直角和基線邊長，再通過三角高程計算公式求得它們之間的高差；GNSS重力高程測量利用測點區域重力資料，通過地球重力場模型求出點位的高程異常，用GNSS所測得的大地高減去高程異常，得到待測點的正常高。在實際工程中，重力數據相對匱乏，其適用性受較大限制。GNSS水準高程是在獲得GNSS大地高和水準測量正常高的基礎上，利用它們之間的轉換關系獲取其余點位正常高的方法，此方法方便高效，精度也有保障，適用范圍較廣。

常用GNSS高程擬合方法有：等值線圖內插法、曲線擬合、曲面擬合(主要有多項式曲面擬合、多面函數擬合，適用于GNSS點呈面狀分布)、地球重力場模型法、神經網絡法等。這類利用數學模型來計算區域內高程異常值方法的主要工作就是構建一個與測區似大地水準面接近程度相對較高的數學模型。

在選用何種擬合方法時，應充分考慮GNSS點的數量、密度和分布狀況[14]；對于道路工程呈帶狀狹長區域的特點，GNSS點呈線狀分布，沿途的似大地水準面屬于連續的曲線，采用曲線擬合方法更為合適。曲線擬合的原理是：由GNSS控制點二維數據和高程異常來構造一個插值函數，求出函數的必要參數，由GNSS所得二維數據來得到高程異常，最后將GNSS所得大地高減去高程異常算得正常高。

曲線擬合方法主要有：多項式曲線擬合、三次樣條曲線擬合、Akima曲線擬合。Akima曲線是在兩個實測點之間進行內插，它需要知道這兩個實測點觀測值和與這兩個實測點相近鄰的四個實測點上的觀測值，此法在已知點數量不多時并不適用，其擬合雖求解效率高，但忽略了一些污染數據的影響，有片面性，其擬合后線型平滑，但求導誤差較大[15]。多項式曲線擬合是線狀分布擬合的主要方法，三次樣條曲線在路線長和控制點多時可構造高次的擬合多項式而避免過于震蕩，故以下著重研究多項式曲線擬合、三次樣條曲線擬合兩種方法。

3.2 GNSS高程擬合精度評定

常用的GNSS高程擬合精度評價主要有內符合精度、外符合精度等[16]。

(1)內符合精度

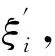
(10)

(2)外符合精度

(11)

4 工程算例

4.1 工程概述

工程算例數據來源于圖3中的藍色某段區間(吳集至龍廟)，路線總長約30.95 km。經搜集已知水準高程資料和現場踏勘確認，選定沿線13個控制點，已知水準高程由四等水準觀測獲得，經過GNSS接收機布網進行靜態觀測，得到橢球高、正常高，出于保密需要，高程數據經過系統處理，見表1。

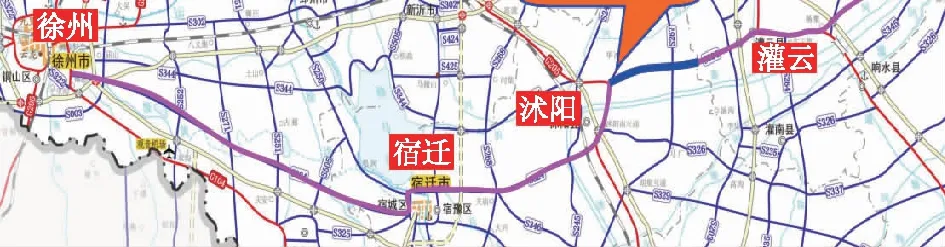
圖3 鐵路整體走向示意

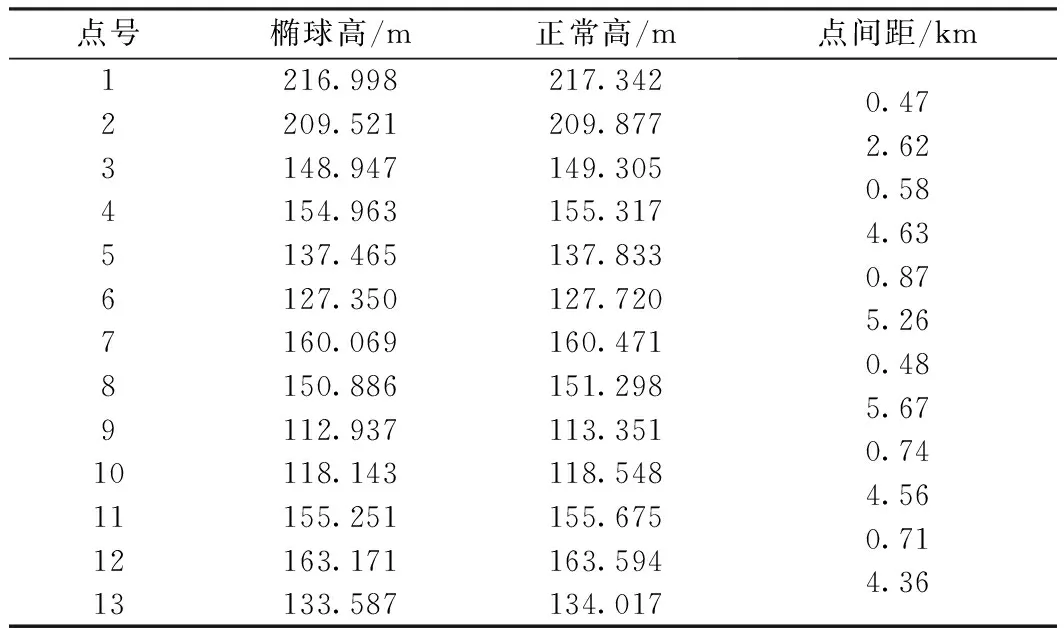
點號橢球高/m正常高/m點間距/km1216.998217.3422209.521 209.8773148.947149.3054154.963155.3175137.465137.8336127.350127.7207160.069160.4718150.886151.2989112.937113.35110118.143118.54811155.251155.67512163.171163.59413133.587134.0170.472.620.584.630.875.260.485.670.744.560.714.36

將數據繪制成如圖4所示的形式。

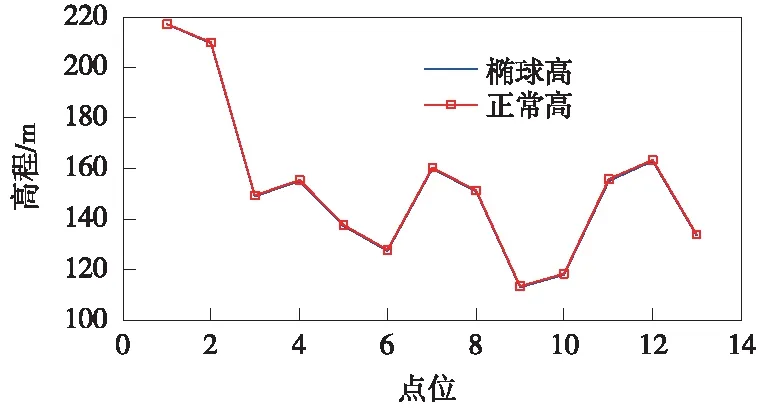
圖4 道路控制點高程折線示意

4.2 多項式曲線擬合

多項式曲線擬合把測區看成一條連續曲線，其本質是一個m次方的代數多項式。可設高程異常值ξ與任意點A(x，y)有以下關系

ξ=f(x)-v

(12)

式中，f(x)為高程異常的數學模型，v為誤差。

設

f(x)=a0+a1x+a2x2+a3x3+……

(13)

當有n個已知點時，上式寫成矩陣形式

V=XB-ξ

(14)

式中

(15)

在Σν2=min限制條件下，依B=(XTX)-1XTξ，可求出向量B和待定系數a0、a1、a2…an；即可計算出未知點高程異常值[17]。數據分別采用二次和三次多項式擬合，過程和結果大致如下。

①二次多項式擬合

依ξ=a0+a1x+a2x2，選取1，5，10，13作為公共點，其余作為檢核點，計算得常數值：ξ=-0.343 9-0.003 004x+0.000 007 014x2

帶入公式后可得各點高程異常和殘差。

②三次多項式擬合

依ξ=a0+a1x+a2x2+a3x3，選取同樣公共點和檢核點，算得常數值：ξ=-0.3463-0.001 867x+0.000 157 4x2+0.000 004 39x3

同理，帶入公式后可得各個點的高程異常值和殘差值。

4.3 三次樣條曲線擬合

當高程異常值波動大、測量線路較長且有一定數量公共點的情況下，求待定系數的誤差會變大。可把測線看成若干個分線段，將每段設為三次多項式函數，然后將多項式函數組成三次樣條函數。處理后不僅函數自身連續，其一階、二階導數也連續[18]。

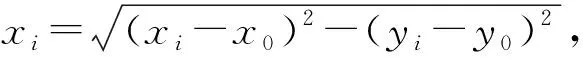
ξ(x)=ξ(xi)+(x-xi)ξ(xi，xi+1)+

(x-xi)(x-xi+1)ξ(x，xi，xi+1)

(16)

其中x為待定點坐標，ξ(xi，xi+1)是一階差商，ξ(xi，xi+1)=(ξi+1-ξi)/(xi+1-xi)；ξ(x，xi，xi+1)為二階差商，ξ(x，xi，xi+1)=1/6[ξ″(xi)+ξ″(x)+ξ″(xi+1]，ξ″(X)=(i=1，2，…，n-1)，其線性方程組具有對稱三角陣的系數矩陣

(xi-xi+1)ξ″(xi-1)+2(xi+1，xi-1)ξ″(xi)+

(xi+1，xi)ξ″(xi+1)=6[ξ″(x，xi+1)-ξ(x，xi)]

(17)

ξ(x0)=ξ″(xn)=0

(18)

用追趕法對其求解，可得ξ″(xi)和ξ(xi，xi+1)

ξ″(x)=ξ″(xi)+(x-xi)ξ″(xi，xi+1)

(19)

ξi，i+1=(ξi+1-ξi)/(xi+1-xi) (i=1，2,…，n-1)

(20)

Ki，i+1=(Ki+1-Ki)/(xi+1-xi) (i=1，2，…，n-1)

求出系數Ki后，就可用下式求得測區內任一點的高程異常，并計算各點正常高

ξ=ξi+ξi，i+1(x-xi)+(x-xi)·

(x-xi+1){2Ki+Ki+1+Ki，i+1(x-xi)}/6

以采用7個控制點分為5段為例，設置每段的三次樣條函數(如圖5～圖9)，橫坐標為5段中某分段的點位，縱坐標為Matlab軟件自動計算的序列點特征量，擬合過程大致如下。

圖5 第一段樣條曲線

同理，得到第二段曲線函數

ξ=-0.001 5t3+0.013 5t2-0.031 2t-0.344 8

圖6 第二段樣條曲線

擬合得到第一條曲線函數

ξ=-0.001 6t3+0.009 7t2-0.008 8t-0.353 8

第三段曲線函數

ξ=0.000 4t3-0.007 6t2+0.046 3t-0.439 6

圖7 第三段樣條曲線

第四段曲線函數

ξ=-0.000 3t3+0.009 8t2-0.098 6t-0.038 7

圖8 第四段樣條曲線

第五段曲線函數

ξ=-0.000 3t3+0.009 4t2-0.0948t-0.0505

圖9 第五段樣條曲線

4.4 兩種方法擬合殘差比較

對道路控制點高程用多項式、三次多項式、三次樣條曲線方法進行擬合分析，擬合值殘差如表2所示。

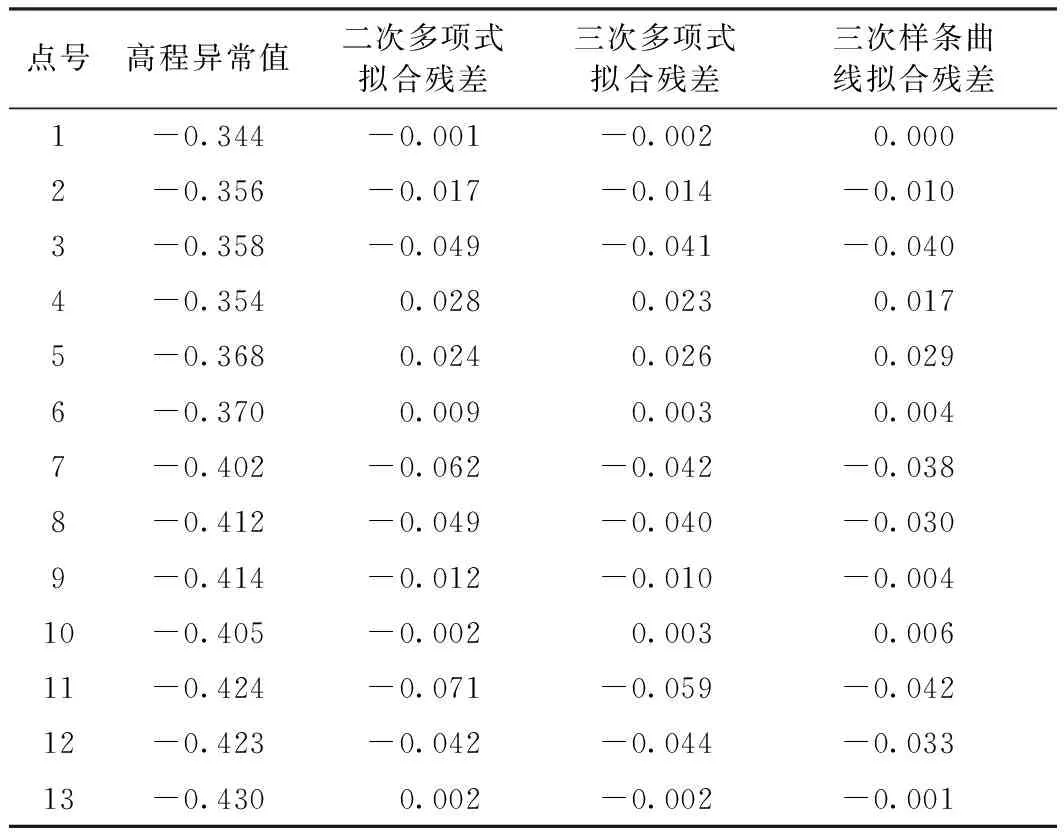
表2 多項式擬合殘差 m

可繪制成如圖10所示的形式。

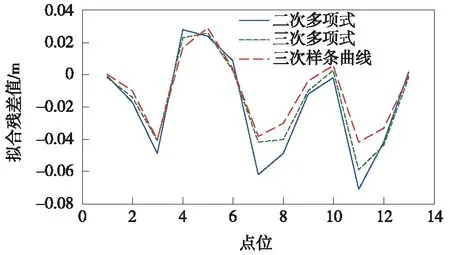
圖10 高程擬合殘差

5 結論

本段線路長度約為30.95 km，相較于傳統水準測量，選用準確高效的GNSS高程擬合方法能極大地節省人力和物力。

選取多項式擬合和三次樣條曲線擬合方法進行鐵路GNSS高程擬合適用且有效；對13個控制點的測試表明，其擬合誤差最大點的殘差值為-0.071 m，若經簡易整體平差改正數按比例反向賦配，改正后的水準高程誤差均在0.04 m以內，對于Ⅱ級及以下等級鐵路基本可以滿足道路工程測量中地形測量、斷面測量和施工測量對于控制點高程的精度要求。

經數據分析比較，二次多項式、三次多項式、三次樣條曲線三種方法的最大擬合殘差依次為：-0.071 m，-0.059 m，-0.042 m；三種方法的殘差均值依次為：-0.019 m，-0.015 m，-0.011 m；依據上述精度評定方法，三種方法的內符合精度依次為0.066 m，0.055 m，0.045 m；外符合精度依次為0.070 m，0.059 m，0.044 m。由此可見，兩種GNSS高程擬合方法的點位擬合殘差平均值都在0.02 m以內，擬合精度較好，且三次樣條曲線擬合效果更優。究其原因，(1)它保留了多項式表達簡便的特點，又解決了單個多項式機械、不靈活的缺點；(2)當線路較長時，即便是高次多項式，其擬合程度也不能明顯提高，而選取更多的插值節點，采用分段低次插值反而可行[19]。

對于較短或者更長距離的高程擬合還有待進一步探討，其他插值方法和組合方法對于鐵道工程GNSS高程擬合的研究還需進一步深入[11，14，15，19]。