基于有限元的分析與配筋法在雙排樁-錨桿 結(jié)構(gòu)設(shè)計(jì)中的應(yīng)用*

董必昌 田智睿付紹卿 王 宇

(武漢理工大學(xué)交通學(xué)院1) 武漢 430063) (武漢中科巖土工程有限責(zé)任公司2) 武漢 430063)

0 引 言

樁錨支護(hù)是一種常見的深基坑支護(hù)方式[1]，這種支護(hù)結(jié)構(gòu)通過錨桿對(duì)排樁提供錨拉力，從而減小支護(hù)排樁的位移與內(nèi)力，并將基坑的變形控制在允許的范圍內(nèi).相比其他支護(hù)結(jié)構(gòu)，樁錨支護(hù)不需加設(shè)內(nèi)支撐，具有變形小、施工簡(jiǎn)易等優(yōu)點(diǎn)，在深基坑工程中得到了廣泛應(yīng)用.

對(duì)于門式雙排樁-錨桿支護(hù)結(jié)構(gòu)的設(shè)計(jì)和受力分析，王惠民等[2]采用有限元軟件，基于Mohr-Coulomb模型，對(duì)雙排樁-錨桿支護(hù)結(jié)構(gòu)深基坑的開挖全過程進(jìn)行了數(shù)值模擬研究，發(fā)現(xiàn)開挖完成時(shí),在樁身中部附近產(chǎn)生最大水平位移；基坑外超載對(duì)基坑支護(hù)影響很大.胡海軍[3]通過數(shù)值模擬的方式，分析了支護(hù)結(jié)構(gòu)在土體開挖荷載作用下的內(nèi)力和變形，為其設(shè)計(jì)和施工提供了參考.胡賀祥等[4]采用適用于敏感環(huán)境下基坑數(shù)值分析的硬化類彈塑性本構(gòu)模型，針對(duì)錨桿對(duì)雙排樁變形和受力的影響進(jìn)行數(shù)值模擬，發(fā)現(xiàn)錨固角度的增加能有效減小雙排樁的最大水平位移和后排樁的樁身控制彎矩，但減小幅度隨錨固角度增大而減小.謝榮昌等[5]結(jié)合具體工程實(shí)例分析了實(shí)際監(jiān)測(cè)數(shù)據(jù)，證明了雙排樁樁錨支護(hù)體系在緊鄰高層建筑深基坑支護(hù)工程中的適用性，為同類工程的方案設(shè)計(jì)與施工提供參考.上述研究主要通過數(shù)值模擬等方法探討了門式雙排樁-錨桿支護(hù)結(jié)構(gòu)的受力特征和工程應(yīng)用，而對(duì)于該結(jié)構(gòu)的配筋設(shè)計(jì)研究涉及較少.在實(shí)際工程中，雙排樁-錨桿結(jié)構(gòu)的受力機(jī)理較為復(fù)雜，文獻(xiàn)[6]中將雙排樁假定為平面剛架結(jié)構(gòu)進(jìn)行計(jì)算，這種假定用于雙排樁-錨桿這種特殊結(jié)構(gòu)時(shí)還不夠合適，故相關(guān)配筋計(jì)算結(jié)果偏向安全和保守.因此，本文以門式雙排-錨桿支護(hù)結(jié)構(gòu)為例，基于有限元法，對(duì)其受力特征和配筋設(shè)計(jì)進(jìn)行了研究，并得出了相關(guān)結(jié)論.

1 雙排樁錨結(jié)構(gòu)數(shù)值模擬

1.1 模型概況

選取武漢時(shí)代廣場(chǎng)深基坑樁錨結(jié)構(gòu)支護(hù)體系進(jìn)行仿真模擬，該工程項(xiàng)目處于漢口沿江大道蘭陵路與黎黃陂路之間.其場(chǎng)地位于長(zhǎng)江左岸一級(jí)階地上，有著較為穩(wěn)定的二元地層結(jié)構(gòu)，上部土層主要為靜水沉積相黏性土，下部為為長(zhǎng)江沖洪積相砂類地層.下伏基巖為志留系泥巖.雙排樁影響范圍內(nèi)地質(zhì)土層自下而上依次為粉砂層，粉土層，粉質(zhì)粘土層，填土層.

基坑開挖深度為16.4 m，采用樁錨支護(hù).支護(hù)樁為鉆孔灌注樁，靠近基坑一側(cè)為前排樁，靠近土體一側(cè)為后排樁，樁間土采用旋噴處理，樁長(zhǎng)為22 m，樁徑為0.9 m，樁心距為2.8 m，樁身嵌入土層8.6 m，約為整個(gè)樁身長(zhǎng)度的2/5.錨桿設(shè)置為三排平行布置，采用預(yù)成孔二次注漿錨桿，預(yù)應(yīng)力張拉鎖緊，錨索位置見表1.

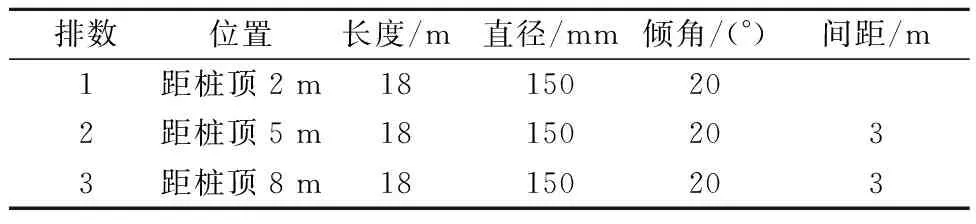
表1 基坑預(yù)應(yīng)力錨桿參數(shù)

對(duì)于模型的計(jì)算范圍，以雙排樁為中心，在橫向?qū)挾?X方向)：底邊長(zhǎng)度為65 m，前排樁樁頂?shù)阶筮吔绲木嚯x為30.5 m，后排樁樁頂?shù)接疫吔绲木嚯x為30.5 m；在橫向高度(Y方向)，左端邊界高為24.7 m，右端邊界高為41.1 m.深基坑支護(hù)模型見圖1，雙排樁和錨桿尺寸見圖2.

圖1 基坑支護(hù)示意圖 (尺寸單位：m)

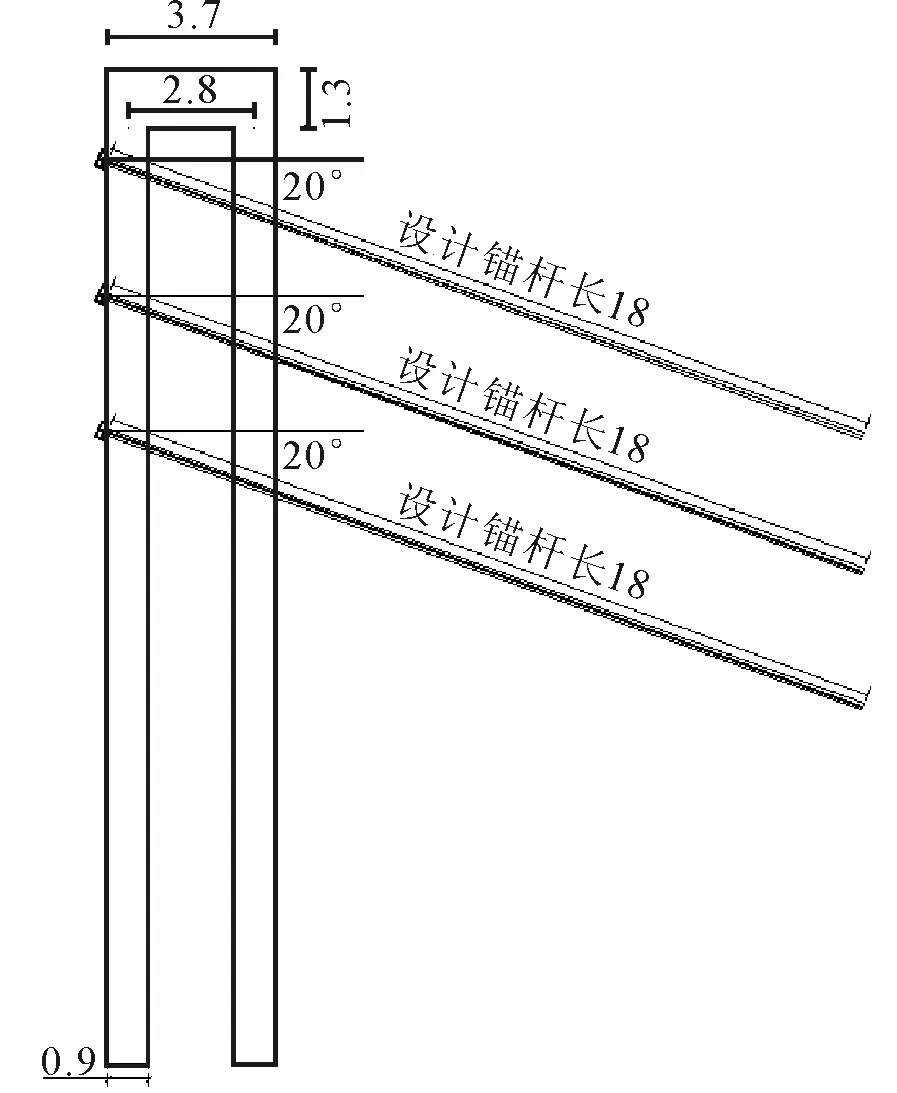
圖2 雙排樁和錨桿尺寸圖 (尺寸單位：m)

1.2 模型建立

由于本文主要對(duì)深基坑和支護(hù)樁進(jìn)行水平方向受力研究，故建立支護(hù)結(jié)構(gòu)的平面模型，且不考慮樁土接觸.模型中土體和雙排樁均采用PLANE82單元模擬，對(duì)于基坑土體的本構(gòu)模型，采用理想彈塑性模型，屈服準(zhǔn)則采用Drucker-Prager[7]準(zhǔn)則，雙排樁和樁身之間的旋噴區(qū)采用線彈性模型，且對(duì)樁身端部的周邊單元進(jìn)行網(wǎng)格加密和平順處理，錨桿采用LINK8[8]單元進(jìn)行模擬，預(yù)應(yīng)力為180 kN，通過定義LINK8單元參數(shù)來輸入錨桿的截面尺寸和預(yù)應(yīng)力值，將錨桿單元與樁土單元進(jìn)行耦合來模擬錨桿錨定的效果.在模型的邊界上，地面和開挖面為自由面，兩邊豎直邊界水平約束，底面全約束，具體模型材料參數(shù)見表2，圖3為有限元模型，圖4為劃分網(wǎng)格后的模型.

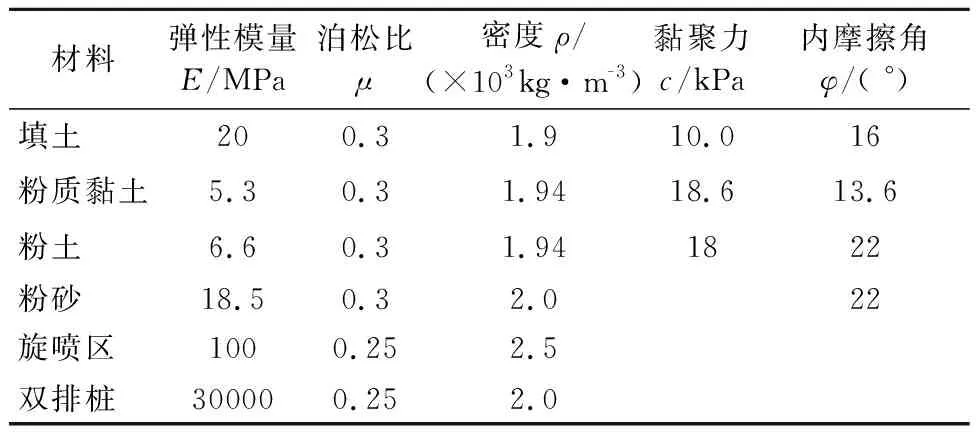
表2 模型材料參數(shù)

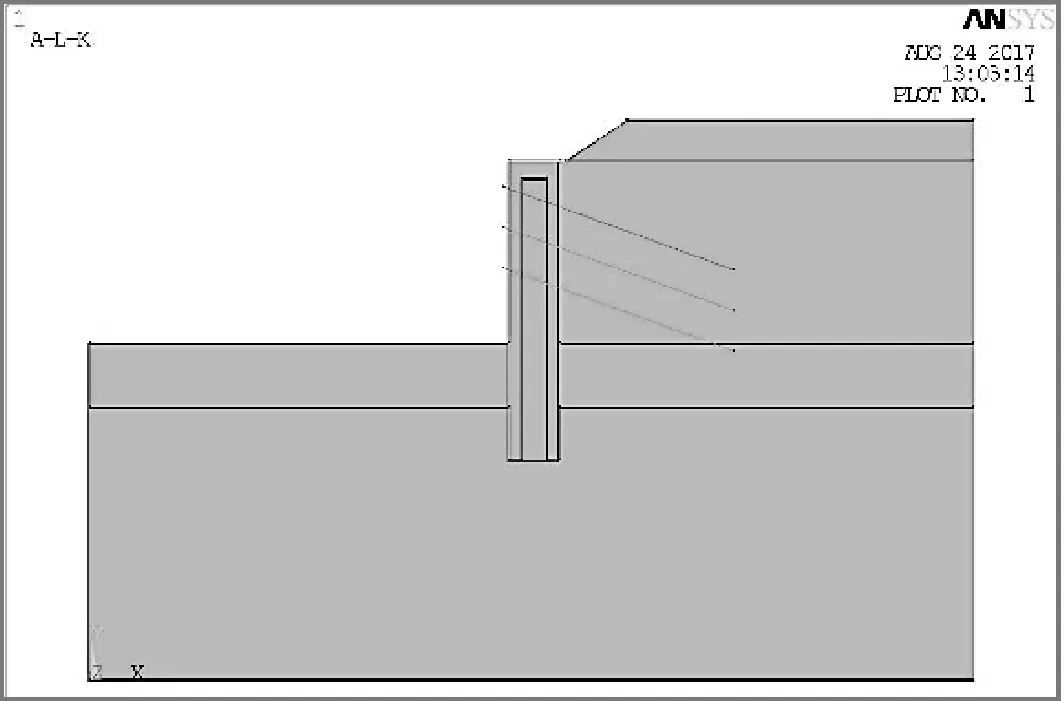
圖3 雙排樁邊坡模型

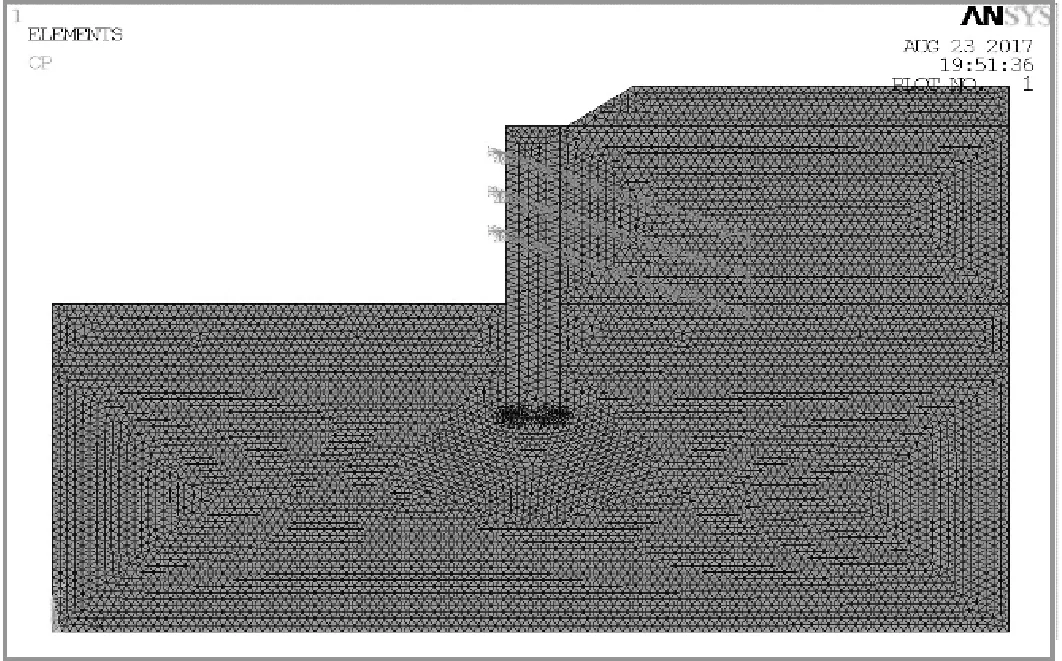
圖4 網(wǎng)格劃分后的模型

2 模型受力特征及變形分析

2.1 基坑土體變形分析

基坑的場(chǎng)地土體在開挖之前就有長(zhǎng)期的自重沉積，使得土體已達(dá)到沉降固結(jié)，為了獲得基坑開挖過程中土體卸載造成的土體沉降，分別建立了基坑開挖之前與基坑開挖后模型，通過相減基坑在開挖前后的沉降值，可去除土體由自重應(yīng)力場(chǎng)作用導(dǎo)致的沉降，并計(jì)算得到基坑由于卸載導(dǎo)致的額外沉降變形，以便于對(duì)基坑整體變形的分析.

圖5為基坑開挖前和開挖后的Y方向位移云圖.由圖5可知，隨著基坑的開挖，基坑內(nèi)測(cè)邊緣土體逐步出現(xiàn)隆起，而基坑外側(cè)土體則因基坑內(nèi)的土體卸載破壞了原有平衡重力場(chǎng)，從而出現(xiàn)沉降，對(duì)比兩個(gè)模型，減去開挖前因重力場(chǎng)造成的沉積變形后可得到由基坑開挖造成的額外沉降為0.8 cm，小于地表沉降警戒值，滿足安全需求.

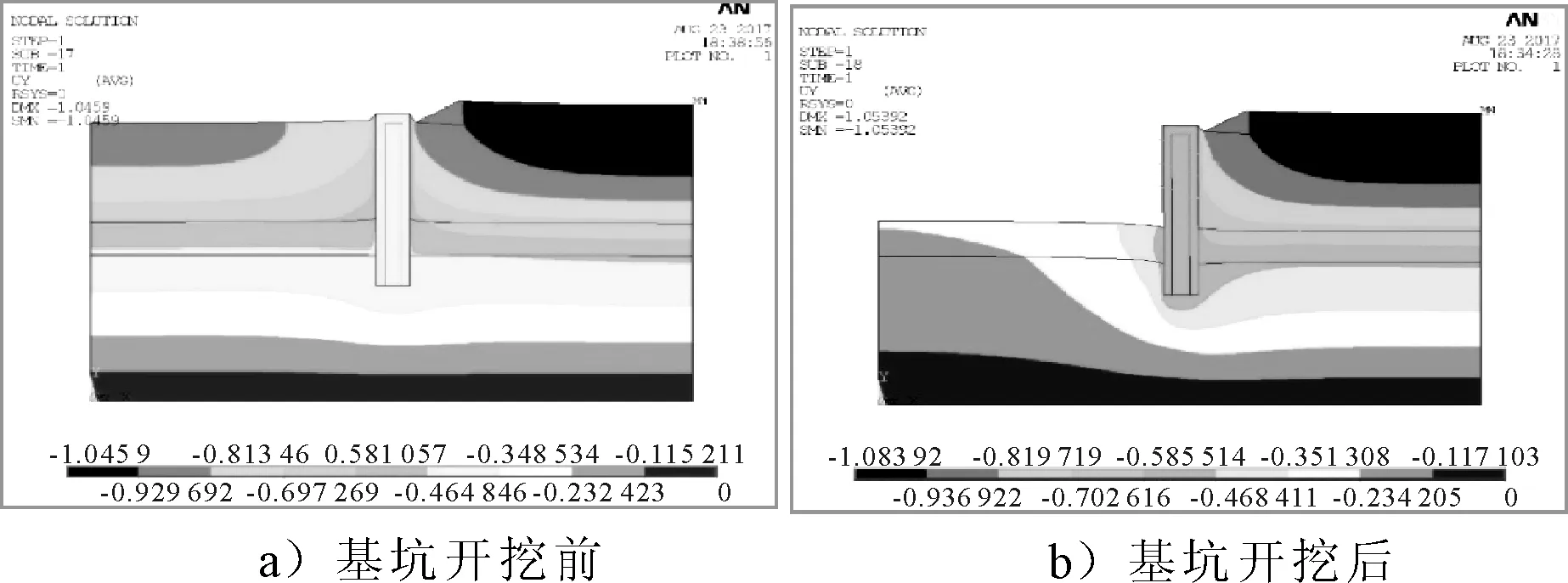
圖5 模型Y向位移云圖 (單位：m)

2.2 雙排樁-錨桿結(jié)構(gòu)受力及變形分析

隨著基坑開挖，基坑內(nèi)側(cè)土體進(jìn)行卸載，從而導(dǎo)致支護(hù)結(jié)構(gòu)的內(nèi)力和位移發(fā)生變化.圖6為基坑開挖完成后，雙排樁樁身的第一主應(yīng)力云圖.由圖6可知，在樁身錨固處以及樁身與嵌入土體交界處應(yīng)力較為集中，前排樁第一主應(yīng)力最大值為2.72 MPa，后排樁第一主應(yīng)力最大值為1.85 MPa.

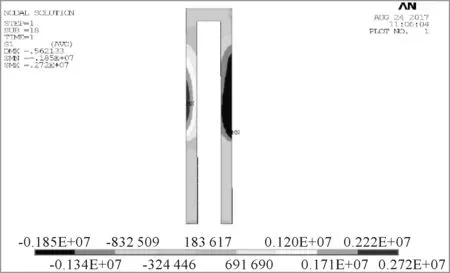
圖6 雙排樁第一主應(yīng)力云圖 (單位：Pa)

圖7為雙排樁剪力云圖.由圖7可知，前、后排樁均在在土層分界面處存在著剪應(yīng)力突變現(xiàn)象，其中前排樁在距樁頂18.22 m處出現(xiàn)最大剪應(yīng)力，值為0.64 MPa；后排樁在距樁頂17.62 m處出現(xiàn)最大剪應(yīng)力，值為0.82 MPa.

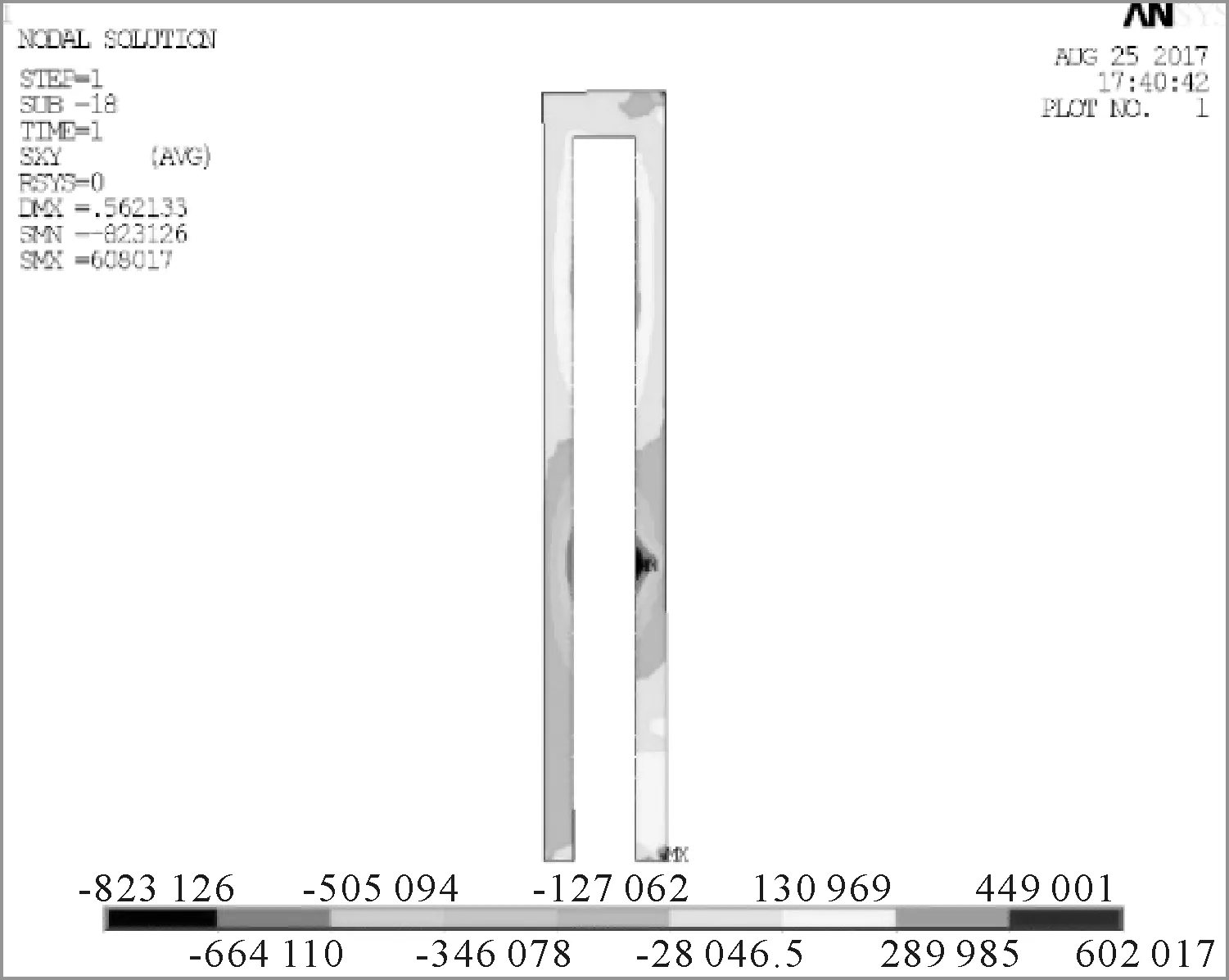
圖7 雙排樁剪力云圖 (單位：N)

圖8為錨桿水平位移云圖.由圖8可知，第二和第三排錨桿上出現(xiàn)最大節(jié)點(diǎn)水平位移為5 cm，且靠近錨桿埋入土層一端的節(jié)點(diǎn)位移較大.圖9為雙排樁水平位移云圖.由圖9可知，身在右側(cè)土體的壓力作用下向基坑內(nèi)側(cè)彎曲變形.前、后排樁均在樁頂處出現(xiàn)最大水平位移，前排樁最大水平位移為為2.1 cm，后排樁最大水平位移為2.0 cm.樁頂以下至基坑底部，樁身水平位移逐漸減小，表明錨桿對(duì)支護(hù)結(jié)構(gòu)的變形起到了抑制作用，使結(jié)構(gòu)達(dá)到了支擋土體的功能.

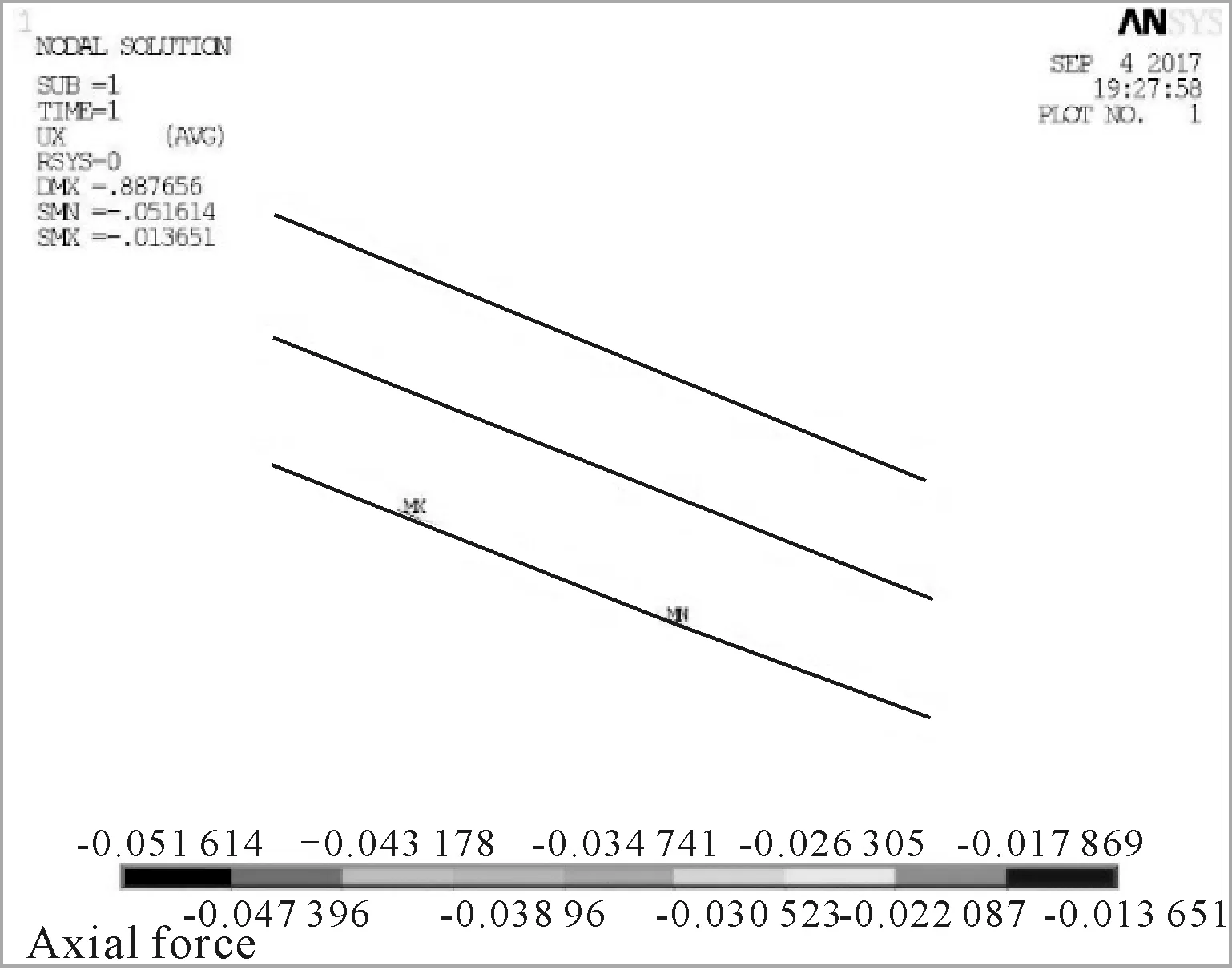
圖8 錨桿水平位移云圖(單位：m)

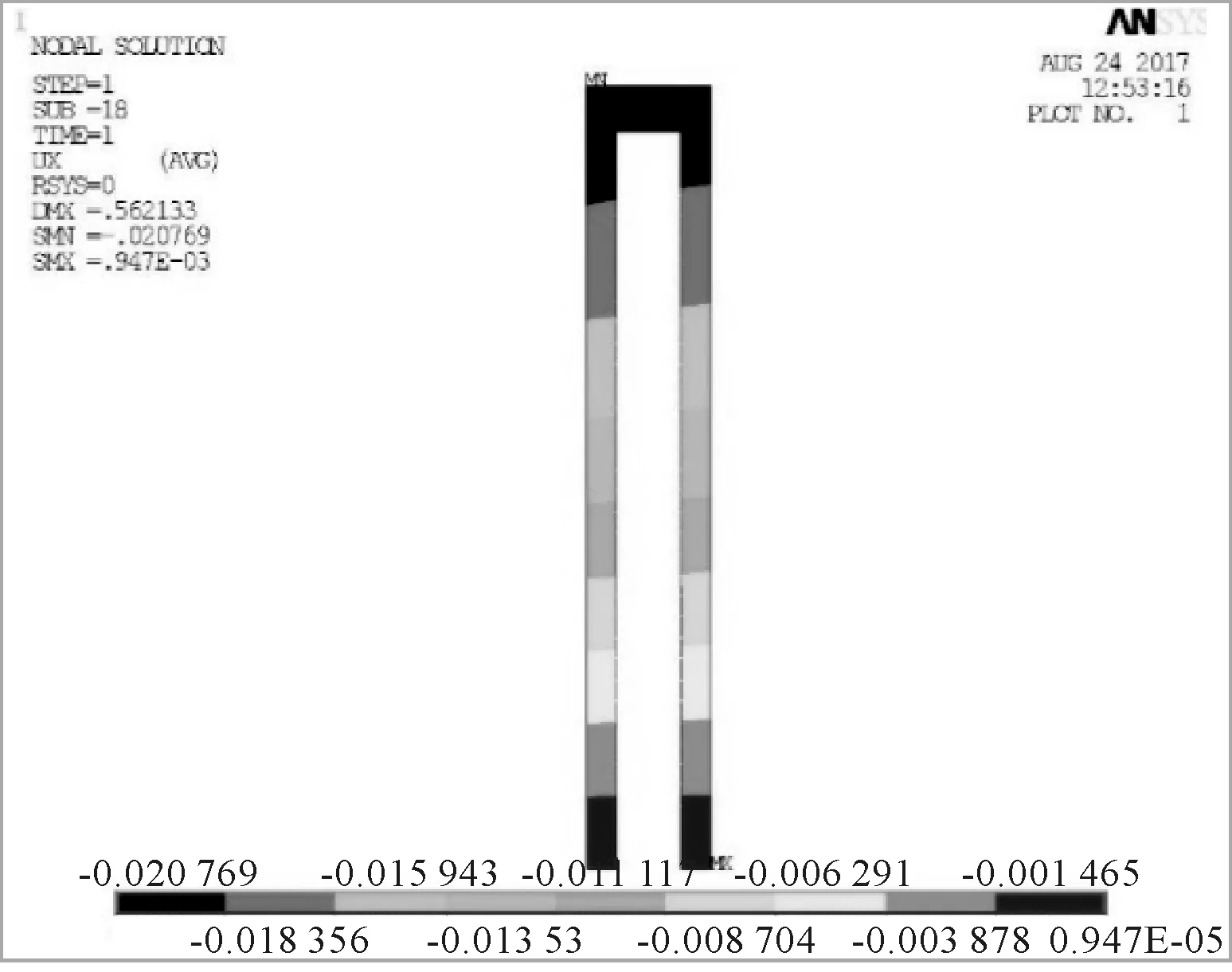
圖9 雙排樁水平位移云圖(單位：m)

3 門式雙排樁-錨桿結(jié)構(gòu)配筋

3.1 基于有限元的雙排樁內(nèi)力計(jì)算

由于門式雙排樁-錨桿結(jié)構(gòu)在實(shí)際支護(hù)過程中的受力機(jī)理較為復(fù)雜，而現(xiàn)有規(guī)范中只是將其簡(jiǎn)化為平面剛架結(jié)構(gòu)進(jìn)行內(nèi)力計(jì)算，這種假定用于雙排樁-錨桿這種特殊結(jié)構(gòu)還不夠合適.而通過建立基坑支護(hù)結(jié)構(gòu)的有限元模型，模型將樁作為彈性體，再根據(jù)有限元計(jì)算得出的彈性體的受力結(jié)果，便可以進(jìn)行配筋.

雙排樁的主筋和箍筋的配筋面積分別根據(jù)樁身所受的剪力和彎矩計(jì)算得到，考慮Ansys軟件只能得出結(jié)構(gòu)各個(gè)節(jié)點(diǎn)的應(yīng)力結(jié)果，不能得出截面受力，故使用Ansys后處理功能將模型中的雙排樁節(jié)點(diǎn)剪力以文本形式導(dǎo)出，采用單元節(jié)點(diǎn)力求和法處理節(jié)點(diǎn)數(shù)據(jù)，即將同一截面上的節(jié)點(diǎn)剪應(yīng)力進(jìn)行累加，從而得出該截面上的剪力，并由此可以求得樁身不同位置處的剪力.

圖10為前、后排樁剪力隨樁身位置變化曲線，前排樁在距樁頂11.8 m處剪力最大，為546.13 kN；后排樁在樁頂8.8 m處剪力最大，為697.85 kN.再對(duì)已經(jīng)得到的剪力曲線面積進(jìn)行累加積分[9]，便可以得出不同樁身截面處所受的彎矩，圖11為前、后排樁彎矩隨樁身位置變化曲線，前、后排樁的彎矩變化趨勢(shì)一致，均為”S”形曲線，前排樁在距樁頂7.7 m處彎矩絕對(duì)值值最大，為1 534.96 kN·m；后排樁在距樁頂11.2 m處彎矩絕對(duì)值最大，為1 459.12 kN·m.

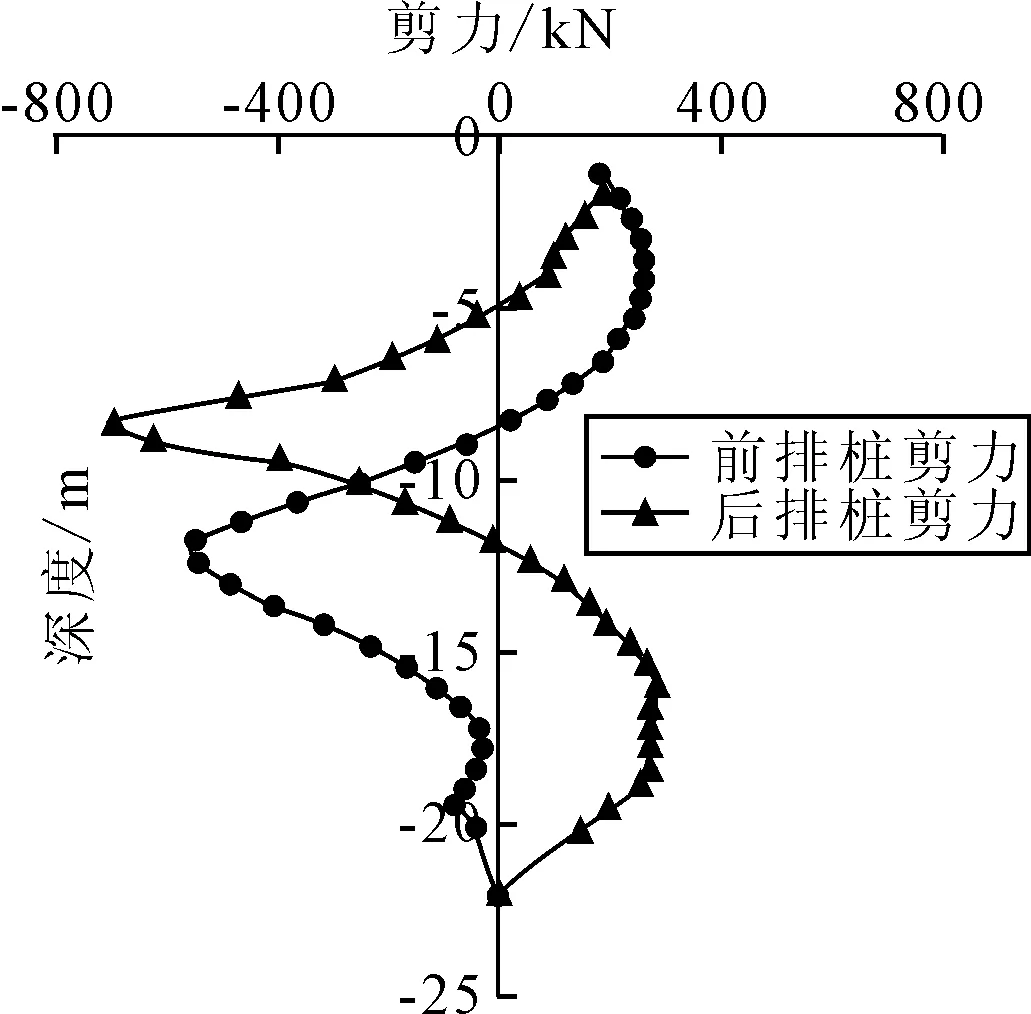
圖10 前、后排樁樁身剪力圖

圖11 前、后排樁樁身彎矩圖

3.2 雙排樁配筋計(jì)算

通過處理有限元模型內(nèi)力結(jié)果得出前、后排樁的最大剪力和彎矩后，便可以出現(xiàn)該剪力和彎矩值的截面作為最不利截面進(jìn)行配筋計(jì)算.根據(jù)文獻(xiàn)[10]中對(duì)于圓形截面樁的配筋原則對(duì)雙排樁進(jìn)行配筋，前排樁主筋25Ф25，箍筋Ф8@200；后排樁主筋24Ф25，箍筋Ф8@200.原工程設(shè)計(jì)采用傳統(tǒng)方法計(jì)算，其前排樁一般截面主筋為14 771 mm2, 后排樁樁一般截面主筋為11 775 mm2；而基于有限元運(yùn)算結(jié)果得到的配筋量為前排樁截面主筋12 270 mm2，比原工程設(shè)計(jì)的配筋量少；后排樁截面主筋11 775 mm2，和原工程設(shè)計(jì)一致，但考慮到原工程前后排樁在坑底4 m上下處主筋增加了12φ25，故可以得出結(jié)論：相比傳統(tǒng)配筋方法，基于有限元的配筋法更加節(jié)省配筋用量，其前排樁截面主筋配筋量可節(jié)省23%，后排樁截面主筋配筋量可節(jié)省10%.

4 結(jié) 論

1) 隨著基坑的開挖，基坑內(nèi)測(cè)邊緣土體逐步出現(xiàn)隆起，而基坑外側(cè)土體則內(nèi)測(cè)土體卸載破壞了原有平衡重力場(chǎng)，從而出現(xiàn)沉降，其最大沉降量為0.8 cm，滿足安全需求.

2) 在樁身錨固處以及樁身與嵌入土體交界處應(yīng)力較為集中，前排樁第一主應(yīng)力最大值為2.72 MPa，后排樁則為1.85 MPa.前、后排樁均在在土層分界面處存在著剪應(yīng)力突變現(xiàn)象，其中前排樁在距樁頂18.22 m處出現(xiàn)最大剪應(yīng)力，值為0.64 MPa；后排樁在距樁頂17.62 m處出現(xiàn)最大剪應(yīng)力，值為0.82 MPa.

3) 前、后排樁均在樁頂處出現(xiàn)最大水平位移，前排樁最大水平位移為為2.1 cm，后排樁最大水平位移為為2.0 cm.由于錨桿的抑制作用，樁頂以下至基坑底部，樁身水平位移逐漸減小.

4) 驗(yàn)證了基于有限元的配筋法的可行性，并發(fā)現(xiàn)相比傳統(tǒng)配筋方法，基于有限元的配筋法更加節(jié)省配筋用量，其前、后排樁截面主筋配筋量分別可節(jié)省23%和10%.