力錘激勵下場地土動力響應系統辨識

曾 宇，鄔玉斌，宋瑞祥，吳 瑞

（北京市勞動保護科學研究所，北京 100054）

隨著我國城市地鐵路網逐步加密，地鐵列車引發的環境振動問題近年來受到廣泛關注。地鐵列車振動通過隧道傳入土體后，振動的傳播和衰減主要在土層中完成，因此研究振動在土體中的傳播和衰減特性是分析、預測地鐵振動對敏感目標影響程度的重要環節[1–2]。

對于土體動力響應的建模和特征分析，學者們進行了一系列的研究。劉衛豐采用直接剛度法，計算了水平成層半空間或全空間土體在點源作用下的動力響應[3]。周鳳璽等利用半解析法，研究了移動荷載作用下二維非均勻彈性半平面地基的動力響應[4]。錢建固等計算了移動荷載作用下飽和多孔介質地基的動力響應，分析了荷載速度和頻率對地基動應力的影響[5]。范留明等將波阻抗界面作為次級子波源，提出了傾斜入射地震波作用下成層場地動力響應的界面子波算法[6]。劉妮娜等基于振動臺模型試驗，研究了地震荷載作用下地裂縫場地的動力響應[7]。王啟耀等以EI Centro波和Taft波為激勵，分析了水平地震作用下地裂縫場地地表加速度響應規律[8]。陳龍偉等以土層厚度和剪切波速為影響因素，分析了土層特性變異對場地動力響應的影響[9]。張建經等研究了小角度成層傾斜場地的地震動響應特征，分析了地層傾角對場地反應譜的影響[10]。范剛等基于振動臺模型試驗，研究了地震作用下成層場地的動力響應[11–12]。

本文基于系統辨識的方法，建模分析場地土的動力響應。結合北京某地鐵環境影響評價項目，鑒于相關地鐵尚未通車運營，以力錘激勵為振動源強通過現場測試獲得場地土加速度響應。分析連續傳遞函數的階數對傳遞函數時域辨識的均方誤差的影響，以均方誤差最小化為準則，確定最優的連續傳遞函數辨識模型及其數學表達式。在此辨識模型基礎上進行場地土傳遞函數增益分析、幅頻響應分析和脈沖響應分析，研究場地土動力響應特性。

1 場地土動力響應試驗

在北京某地鐵環境振動影響評估項目中，在建地鐵線路采用盾構隧道結構，地塊中敏感建筑與地鐵的距離分別為10 m和19.5 m。由于地鐵尚未通車運營，因而以力錘激勵為振動源強分析地塊中敏感建筑所在位置的場地土動力響應特性。在地表設置激勵點，人工施加力錘激勵，通過力傳感器獲取激勵力信號。在距離激勵點10 m和19.5 m處的地表分別設置加速度響應測點，安裝加速度傳感器。力傳感器和加速度傳感器的采樣頻率均為2 048 Hz。

試驗過程中在激勵點敲擊了5次，敲擊的間隔約為2 s，激勵力信號如圖1所示。

圖1 激勵力時域信號

力信號曲線有5個峰值，與敲擊次數一致。峰值分別出現在1.4s、3.6 s、5.6 s、7.7 s和9.7 s，與力錘敲擊的間隔時間相吻合。峰值分別為3 572.7 N、4 475.9 N、4 932.4 N、4 871.2 N和4 337.6 N，其均值為4 438.0 N，極差為1 359.7 N，標準差為546.0 N。

距激勵點10 m的近處響應測點的加速度信號如圖2所示。

與激勵力信號峰值出現時間相對應，加速度信號曲線有5個峰值。峰值分別為0.091 0 m/s2、0.101 1 m/s2、0.102 1 m/s2、0.100 6 m/s2和 0.089 3 m/s2，其均值為 0.096 8 m/s2，極差為 0.012 8 m/s2，標準差為0.006 14 m/s2。

距激勵點19.5 m的遠處響應測點的加速度信號如圖3所示。

圖2 近處響應測點加速度時域信號

圖3 遠處響應測點加速度時域信號

與激勵力信號峰值出現時間相對應，加速度信號曲線有5個峰值。峰值分別為0.034 3 m/s2、0.035 7 m/s2、0.044 6 m/s2、0.051 6 m/s2和 0.041 7 m/s2，其均值為 0.041 6 m/s2，極差為 0.017 3 m/s2，標準差為0.007 02 m/s2。

2 場地土動力響應系統辨識

2.1 連續傳遞函數參數辨識

地鐵環境振動的量級較小，土層完全處于彈性應變階段，所以土層的振動傳遞特性與輸入荷載的大小及頻域分布無關，僅與土層的固有特性有關[13]。傳遞函數能表征系統的動態性能，且只取決于動力系統的固有特性，與激勵量和響應量的形式和大小無關，因而成為研究土層中振動傳播和衰減規律的有效工具[14–15]。

場地土力錘激勵動力響應試驗中的激勵量是激勵力時域信號，響應量是各響應測點的加速度時域信號，傳遞函數為零初始條件下響應量的拉普拉斯變換與激勵量的拉普拉斯變換之比[15]，即

式中：s為拉普拉斯變量，T(s)為傳遞函數，R(s)和F(s)分別為加速度響應信號和激勵力信號的拉普拉斯變換。

采用微分方程對場地土動力系統進行建模，該系統的傳遞函數可以表示為拉普拉斯變量的分式型有理式[15]，即

式中：m和n分別為傳遞函數分子多項式和分母多項式的階數，ai(i=0…m)和bj(j=0…n)為傳遞函數的系數。該傳遞函數模型為連續傳遞函數模型，指定傳遞函數分子多項式和分母多項式的階數后利用MATLAB軟件的系統辨識工具箱中的函數tfest可以進行傳遞函數參數辨識[16]。該函數以響應量和激勵量的時域信號或頻域信號為輸入，對于指定的m和n，基于非線性最小二乘法計算連續傳遞函數系數ai(i=0…m)和bj(j=0…n)及其對應的連續傳遞函數模型Tm,n(s)。

2.2 連續傳遞函數階數影響分析

均方誤差是評估辨識模型的指標，反映辨識模型的偏差程度。連續傳遞函數的階數是連續傳遞函數模型分母多項式的階數，其大于連續傳遞函數模型分子多項式的階數，從而可以得到場地土動力系統n階連續傳遞函數模型的均方誤差，即

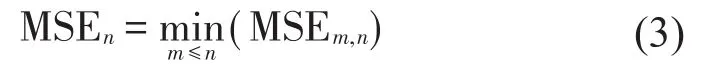
式中：MSEn為該系統n階連續傳遞函數模型的均方誤差，MSEm,n為該系統連續傳遞函數模型Tm,n(s)的均方誤差。

連續傳遞函數模型的階數為2～30時，近處響應測點和遠處響應測點對應的連續傳遞函數模型的均方誤差如圖4所示。

圖4表明隨著階數增加，系統連續傳遞函數模型的均方誤差呈現先減小后增大的趨勢，階數為8時均方誤差最小；階數大于15時連續傳遞函數模型的均方誤差顯著增加，表明此時實測加速度與模型計算的加速度之間偏差變大，辨識模型的質量有所下降。

圖4 場地土各階連續傳遞函數模型的均方誤差

2.3 場地土連續傳遞函數辨識模型及其數學表達式

連續傳遞函數階數對場地土動力系統傳遞函數均方誤差的影響分析表明階數為8時均方誤差最小，從而有

式中MSE為該系統連續傳遞函數模型的最小均方誤差，MSEm,8為該系統連續傳遞函數模型Tm,8(s)的均方誤差。m在不同取值情況下各響應測點連續傳遞函數模型Tm,8(s)的均方誤差如圖5所示，圖5表明m為8時 MSEm,8最小。

圖5 場地土連續傳遞函數模型Tm,8(s)的均方誤差

基于均方誤差最小化準則，近處響應測點和遠處響應測點場地土傳遞函數辨識模型為連續傳遞函數模型T8,8(s)，將其代入式（1）可得

式中：連續傳遞函數的系數bj(j=0，…，8)和ai(i=0，…，8)如表1所示。

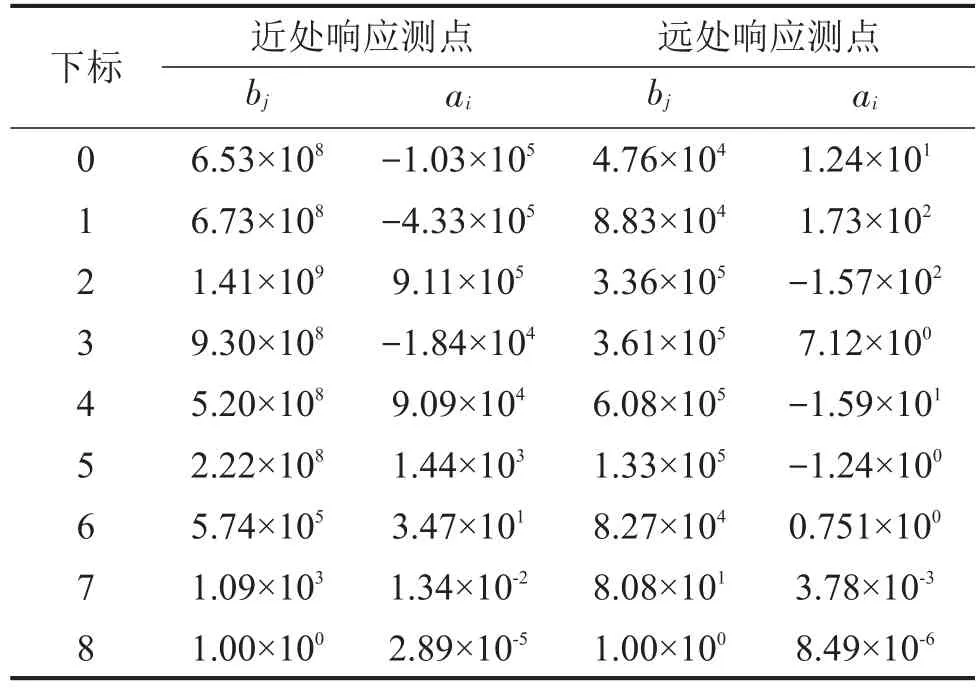
表1 場地土動力響應連續傳遞函數辨識模型參數

近處響應測點和遠處響應測點對應的連續傳遞函數辨識模型的均方誤差分別為1.246×10-5和3.762×10-6，表明實測加速度和根據辨識模型計算所得的加速度之間偏差較小，辨識模型能較好反映相應測點處的場地土動力響應特性。

3 場地土動力響應特性分析

3.1 傳遞函數增益分析

基于場地土動力響應辨識模型，計算得到近處響應測點和遠處響應測點對應的傳遞函數增益分別為2.89×10-5和8.49×10-6。數據表明傳遞函數增益受響應點和激勵點之間距離的影響，近處響應測點對應的傳遞函數增益大于遠處響應測點對應的傳遞函數增益。

3.2 幅頻響應分析

基于場地土動力響應辨識模型，將復頻域上的連續傳遞函數轉換到頻域上，得到近處響應測點和遠處響應測點處的場地土幅頻響應如圖6所示。

圖6 場地土幅頻響應

采用半功率帶寬法，計算場地土的阻尼比[12]。近處響應測點振動的主頻為0.85 Hz，其前后0.707倍峰值處對應的頻率分別為0.76 Hz和1.02 Hz，阻尼比為15.3%。遠處響應測點振動的主頻為0.52 Hz，其前后0.707倍峰值處對應的頻率分別為0.51 Hz和0.53 Hz，阻尼比為1.9%。近處響應測點的阻尼比大于遠處響應測點的阻尼比，近處響應測點振動衰減更快。

3.3 脈沖響應分析

在激勵點處施加脈沖激勵，基于場地土動力響應辨識模型計算得到近處響應測點和遠處響應測點的振動加速度如圖7所示。

圖7 場地土脈沖響應

近處響應測點振動加速度最大值和最小值分別為8.65×10-3m/s2和-1.78×10-2m/s2,遠處響應測點振動加速度最大值和最小值分別為3.09×10-3m/s2和-2.10×10-3m/s2。近處測點的響應大于遠處測點的響應，與傳遞函數增益分析的結論吻合。

近處響應測點和遠處響應測點的振動加速度都在初始時刻幅值最大，之后振蕩衰減。近處響應測點加速度曲線在1.95×10-3s出現首個正峰，峰值為初始時刻響應幅值的48.6%；遠處響應測點加速度曲線在1.03×10-2s出現首個負峰，峰值為初始時刻響應幅值的68.0%。近處響應測點振動以高頻為主，衰減較快；遠處響應測點振動以低頻為主，衰減較慢。

4 結語

本文采用系統辨識的方法對場地土動力響應進行建模和分析。結合北京某地鐵環境影響評價項目，鑒于相關地鐵尚未通車運營，以力錘激勵為振動源強，現場實測場地土加速度響應。研究傳遞函數階數對傳遞函數模型的均方誤差的影響，基于均方誤差最小化準則，獲得最優連續傳遞函數辨識模型及其數學表達式。基于場地土動力響應辨識模型，進行場地土傳遞函數增益分析、幅頻響應分析和脈沖響應分析。結果表明：

(1)隨著階數增加，系統連續傳遞函數模型的均方誤差呈現先減小后增大的趨勢。

(2)階數大于15時連續傳遞函數模型的均方誤差顯著增加，實測加速度與根據模型計算所得的加速度之間偏差變大。

(3)與激勵點距離較近的測點的傳遞函數增益較大，振動以高頻為主且衰減較快。

(4)與激勵點距離較遠的測點的傳遞函數增益較小，振動以低頻為主且衰減較慢。