數學能力的改善：針對工作記憶訓練的元分析*

郭麗月 嚴 超 鄧賜平

?

數學能力的改善：針對工作記憶訓練的元分析*

郭麗月 嚴 超 鄧賜平

(華東師范大學 心理與認知科學學院, 上海 200062)

工作記憶訓練指針對工作記憶各成分進行的訓練, 以實現個體記憶與其他認知能力的提升。該領域一直都是研究者關注的熱點, 越來越多的研究正在試圖利用工作記憶訓練改善個體的數學能力。然而回顧過往的研究, 發現研究所關注的數學能力類型、針對的被試人群、使用的方法、結論等存在較大差異, 目前尚沒有系統性綜述專門探討工作記憶訓練對數學能力的影響。因此, 本文首先回顧和數學能力有關的工作記憶訓練方式, 然后結合元分析, 從數感、運算能力和數學推理能力三個方面, 分別回顧歸納工作記憶訓練對數學能力的提升作用。具體而言, 盡管研究數量相對有限, 工作記憶訓練可能有效改善數感, 其效應量為中等(Cohen’s= 0.51); 而可能無法有效改善運算和數學推理能力, 它們的效應量小(運算：Cohen’s= 0.04; 數學推理：Cohen’s= ?0.06)。此外, 訓練目標類型與訓練效果有著密切的聯系。

工作記憶訓練; 數學能力; 數感; 運算; 數學推理

1 引言

工作記憶訓練指對存儲系統(包括語音回路(phonological loop)、視空模板(visuospatial sketchpad))或中央執行系統(包括轉換(shifting process)、刷新(updating)和抑制(inhibition)成分)的訓練, 通過提升個體工作記憶容量或工作記憶資源使用效率, 從而產生遷移效應(von Bastian, Langer, J?ncke, & Oberauer, 2013; 黎翠紅, 何旭, 郭春彥, 2014; 劉春雷, 周仁來, 2012)。常見的訓練模式主要有兩大類, 一類是針對單一系統(如語音回路)進行訓練, 另一類針對多種系統(如語音回路與視空模板)進行同時訓練。

工作記憶在數學能力的發展中發揮重要作用, 研究顯示不論是成人還是兒童, 正常發展還是發展障礙兒童, 工作記憶所有子成分的加工過程都與數學表現的優劣(比如運算)存在密切聯系(Friso-van den Bos, van der Ven, Kroesbergen, & van Luit, 2013; Raghubar, Barnes, & Hecht, 2010)。鑒于此, 研究者開始逐步關注工作記憶訓練對數學能力的提升或者改善效果。盡管, 過去有綜述和元分析探討了工作記憶訓練對數學能力的提升效果(Peijnenborgh, Hurks, Aldenkamp, Vles, & Hendriksen, 2016; Schwaighofer, Fischer, & Bühner, 2015; 劉春雷, 周仁來, 2012), 但其或者只從數學能力的單個維度探討, 或者一概而論。事實上數學能力是一個多維概念, 涉及數感、運算能力和數學推理能力等多個層面(Geary, 2006)。過去的研究結果存在很大的異質性, 具體來說, 不同的研究關注數學能力的不同層面(如數感、運算和數學推理), 納入不同特征的被試群體(如不同年齡、心理發展狀況)、使用不同的干預手段, 都可能會導致不同的研究結論(Alloway, 2012; Ang, Lee, Cheam, Poon, & Koh, 2015; Bergman-Nutley & Klingberg, 2014; Dahlin, 2013; Dunning, Holmes, & Gathercole, 2013; Harrison et al., 2013; Kroesbergen, Van’t Noordende, & Kolkman, 2012, 2014; Kytt?l?, Kanerva, & Kroesbergen, 2015; Nelwan & Kroesbergen, 2016; Redick et al., 2013; Robert et al., 2016; S?derqvist & Nutley, 2015; Witt, 2011)。因此, 從單一維度或者籠統地探討工作記憶訓練對于數學能力的作用可能會阻礙我們對于工作記憶訓練遷移效果的理解。然而, 目前尚未有綜述專門針對數學能力這些不同層面的遷移效應做過系統地概括和探討。本文試圖從數感、運算和數學推理這三個層面著手, 結合元分析的研究方法, 深入探討工作記憶訓練對數學能力的提升和改善效果, 并分析影響訓練效果的可能因素, 在前人工作記憶訓練元分析的基礎上(Melby- Lerv?g & Hulme, 2013; Peijnenborgh et al., 2016; Schwaighofer et al., 2015), 我們將聚焦考察年齡、被試類型、訓練目標、訓練任務、控制組類型、訓練強度、訓練頻率、每次訓練時長和訓練持續時間對訓練效果的影響。

2 工作記憶的訓練任務

在介紹工作記憶訓練對不同數學能力的提升效果之前, 我們首先回顧與數學能力有關的工作記憶訓練方式, 以更好理解工作記憶的訓練類型及訓練目標, 本文主要從工作記憶單一系統以及多系統的這兩個訓練模式進行總結。

2.1 單一成分訓練任務

2.1.1 語音回路

分類工作記憶廣度任務(Categorization Working Memory Span task, CWMS)分類工作記憶廣度任務適用于9~86歲的被試群體(Borella, Carretti, & De Beni, 2008; Giofrè, Mammarella, & Cornoldi, 2013), 其訓練周期一般為3個系列, 每個系列持續時間大約60分鐘。在每個系列中, 被試將會完成一項任務, 這項任務包含有一系列以語音形式呈現的詞語, 被試被要求記住這些詞語, 待詞語呈現完畢后將任務要求回憶的詞語寫出來(如圖1所示)。三項任務的廣度都為2~5個單元, 即呈現的詞語在2~5個之間變化 (Borella, Carretti, Riboldi, & De Beni, 2010)。

2.1.2 視空模板

(1) 找不同(Odd One Out, OOO)

找不同任務, 適用的年齡范圍為4~22歲(Alloway, Gathercole, Kirkwood, & Elliott, 2008)。任務會呈現三個圖形, 其中一個形狀與另外兩個不同(如圖2-A), 被試需要辨認出不同的圖形并記住它所在的位置, 當每次所有刺激呈現完畢之后, 會呈現空白方格(如圖2-B), 要求被試在上面指出那個不同圖形所對應的位置。任務難度通過增減試次中刺激的呈現數量來進行調整, 同時, 被試所需記憶的圖形數量也隨之改變。這項任務的主要指標是廣度, 即被試最多能夠正確回憶多少個不同刺激所在位置。

在van der Molen, van Luit, van der Molen, Klugkist和Jongmans (2010) 的訓練中, 被試每周接受3次訓練, 每次6分鐘, 持續5周, 訓練難度從1到7單元逐步遞增, 并隨著被試的表現而改變。

(2) Cogmed JM

Cogmed是應用最為廣泛的工作記憶訓練程序(www.cogmed.com), Cogmed工作記憶訓練包含3個版本, 分別為Cogmed JM 、Cogmed RM和Cogmed QM, 其中Cogmed JM(如圖3所示)專門針對視空模板進行訓練。在Cogmed JM中, 每天訓練15~20分鐘, 每周訓練5天, 持續訓練5周, 適用人群為4~6歲的學前兒童。訓練包括7個視空間工作記憶任務, 具體為水塘任務(Pool)、動物任務(Animals)、碰碰車任務(Bumper Cars)、過山車任務(Rollercoaster)、摩天輪任務(Ferris Wheel)、旅館任務(Hotel)、旋轉任務(Twister)。以動物任務為例, 任務以轉盤為背景, 在轉盤上有8種動物, 這些動物以隨機的順序變亮, 要求受訓兒童按呈現順序依次點擊。

圖1 廣度為3的CWMS任務范例(Borella et al., 2010; Carretti, Cornoldi, De Beni, & Palladino, 2004)。詞語以每秒1個呈現, 聽到動物詞語時輕擊桌面, 并記住每個系列中的某個詞匯, 詞語系列之間的時間間隔為2秒。所有詞語系列呈現完畢后, 回憶所有要求記住的詞匯。

圖2 廣度為2的找不同任務范例 (Henry, 2001)。A)刺激; B)反應卡片。先呈現反應卡片, 之后呈現刺激, 要求指出每行中不同的圖形并記住其位置, 之后在反應卡片上指出不同圖形對應位置。

2.1.3 刷新

(1) N-back任務

N-back任務根據刺激呈現的形式, 可以分為視覺N-back任務和聽覺N-back任務。一些研究進行一種形式的N-back任務訓練, 如視覺空間位置的N-back訓練(Jaeggi, Buschkuehl, Jonides, & Shah, 2011), 在訓練中, 呈現6個位置, 一只青蛙隨機在這6個位置出現, 要求判斷每一次青蛙出現的位置與此前第n次出現時所在的位置是否一樣(見圖4)。也有研究使用雙N-back任務, 如同時呈現視覺的位置和聽覺的字母進行訓練(Jaeggi, Buschkuehl, Jonides, & Perrig, 2008), 視覺的任務為在8個位置呈現方塊, 要求判斷每一次出現方塊的位置是否與此前呈現過的第n個方塊所在的位置一致, 與此同時, 聽覺上呈現字母語音, 要求判斷當前所聽到的字母與之前聽到的第n個字母是否一樣(見圖5)。

在研究中, N-back的指標主要包括被試所能達到的水平n, 正確率與反應時。在不同研究中, 訓練強度有所不同, 一般每次的訓練時間范圍大概在10~45分鐘, 訓練次數為8~20次, 在訓練中, 任務難度與被試的表現相匹配, 訓練結束給予一定的獎勵。

(2) 活動記憶任務(Running Memory, RM)

活動記憶任務最早由Pollack, Johnson和Knaff (1959)設計, 任務以視覺或聽覺方式呈現一系列未知長度的項目串后, 要求按順序回憶一個指定長度的項目串。比如在屏幕中呈現字母串Q、A、I、N、D、T, 之后要求回憶最后三個字母, 即NDT。任務的刺激內容包括字母、數字、位置或圖片, 可通過改變項目串的長度和指定回憶的長度, 或者刺激呈現的時間長短來改變任務難度。活動記憶任務在研究中用于6~75歲的被試群體(Ang et al., 2015; Jahanshahi, Saleem, Ho, Fuller, & Dirnberger, 2008)。

活動記憶任務的指標同樣為廣度, 該任務訓練刷新能力, 在趙鑫等人(趙鑫, 王一雪, 劉丹瑋, 周仁來, 2011)的研究中, 每天訓練15~20分鐘, 每周3~4次, 共完成15次的訓練。

圖3 Cogmed JM (Pearson Inc., www.cogmed.com)

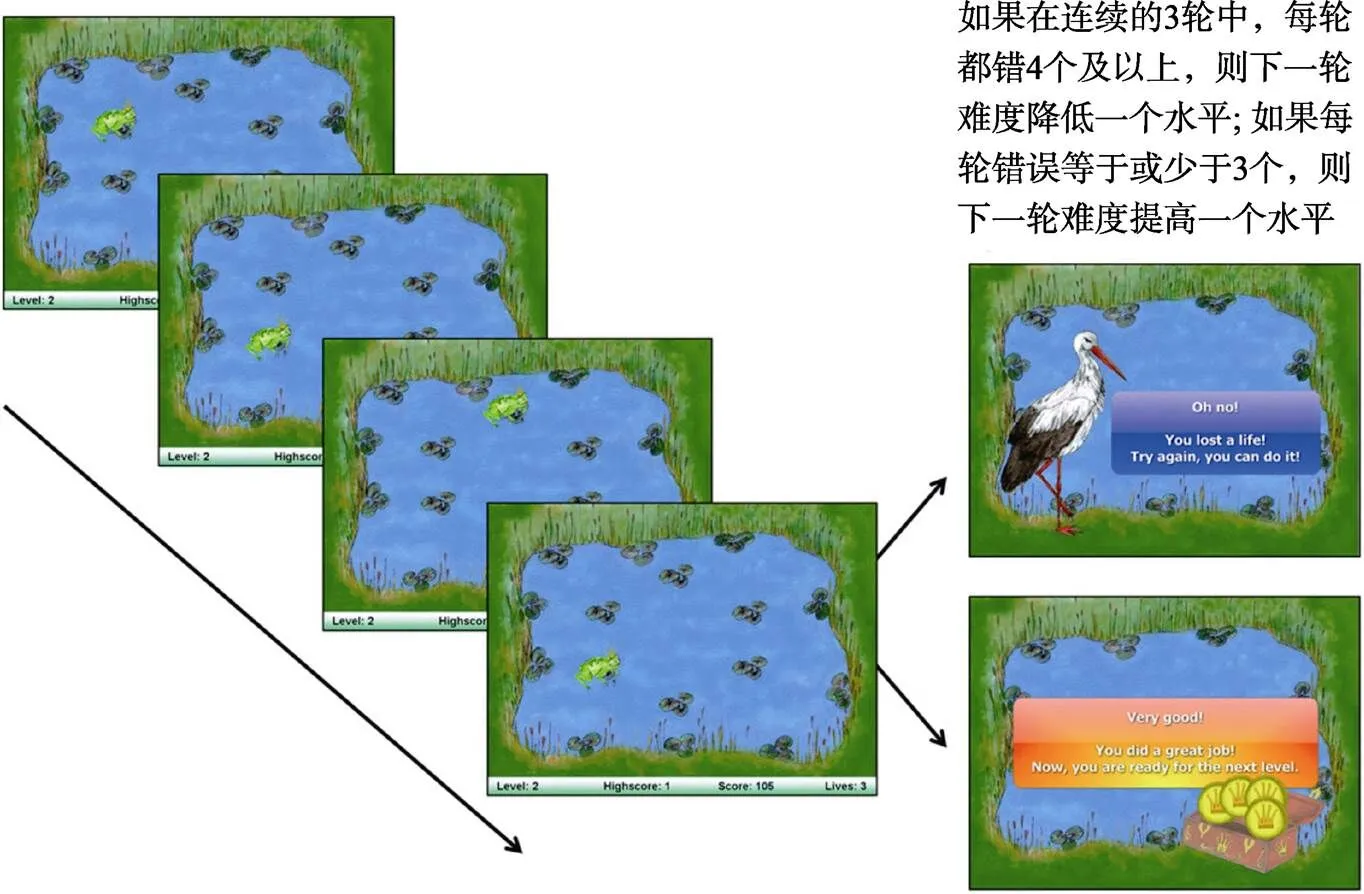
圖4 空間n-back (Jaeggi et al., 2011)。青蛙在6個位置隨機出現, 呈現時間500 ms, 試次之間的時間間隔2500 ms。每個回合有15+n個試次, 每個試次中要求判斷每一次青蛙出現的位置與此前第n次出現時所在的位置是否一樣。

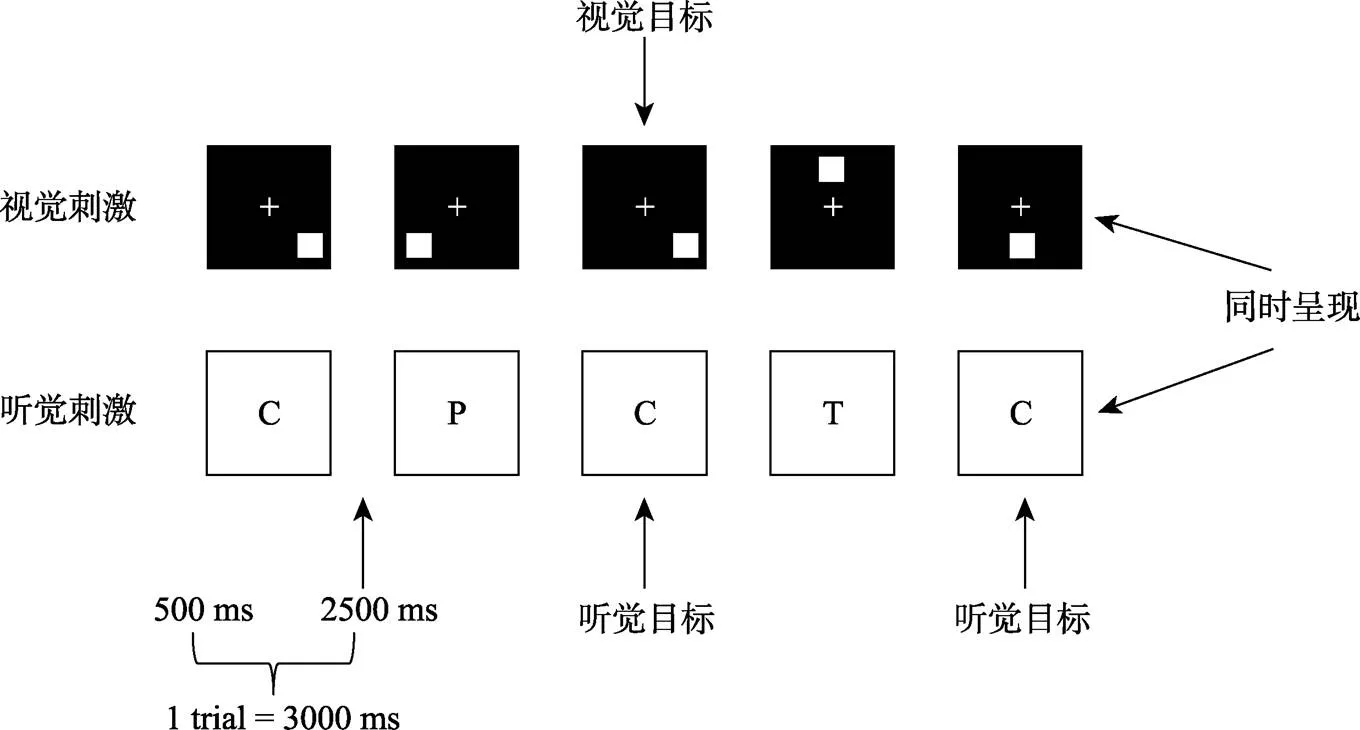
圖5 雙N-back范例(Jaeggi et al., 2008)。同時呈現視覺的位置和聽覺的字母任務, 視覺的任務為在8個位置呈現方塊, 要求判斷每一次出現方塊的位置是否與此前呈現過的第n個方塊所在的位置一致, 一致時按“A”鍵, 與此同時, 聽覺上呈現字母語音, 要求判斷當前所聽到的字母與之前聽到的第n個字母是否一樣, 一樣時按“L”鍵。

2.2 多成分訓練任務

2.2.1 Cogmed工作記憶訓練(Cogmed Working Memory Training, CWMT)

Cogmed工作記憶訓練的另外兩個版本為Cogmed RM和Cogmed QM (見表1), 其中Cogmed RM版本每天訓練30~45分鐘, 針對7~18歲的學齡兒童和青少年設計, 包括13個言語工作記憶和視空間工作記憶任務, 這些任務分別為資料室任務(Data room)、編碼者任務(Decoder)、分類者任務(Sorter)、3D立方體任務(3D cube)、行星游戲(Asteroids)、旋轉數字連線任務(Rotating data link)、旋轉點陣任務(Rotating dots)、太空漫步游戲(Space Whack)、輸入模式任務(Input module)、視覺數字連線任務(Visual data link)、限制輸入模式任務(Input module with lid)、校正者任務(Corrector)、平衡桿游戲(Stabilizer)。以視覺數字連線任務為例(見圖6-A), 表盤上的紅燈以隨機順序亮起, 呈現完之后要求按順序依次點擊這些變亮的燈。Cogmed QM每天訓練30~45分鐘, 適用于成人, 訓練任務包括扭動任務(Twist)、3D網格任務(3D Grid)、校正任務(Correct)、隱藏任務(Hidden)、立方體任務(Cube)、分類任務(Sort)、彈出任務(Pop-Up)、網格任務(Grid)、數字任務(Numbers)、字母任務(Letters)、旋轉任務(Rotating)、混沌任務(Chaos)、組裝任務(Assembly)等13個任務。例如隱藏任務(見圖6-B), 受訓者在聽到一系列的數字之后, 需要按順序在表盤上點擊這些數字。以上兩個版本的訓練強度均是每周訓練5天, 持續5周。

表1 Cogmed三個版本的比較

圖6 Cogmed 任務界面(Pearson Inc., www.cogmed.com)。A)視覺數字連線, 表盤上的紅燈以隨機的順序變亮, 要求按順序依次點擊這些變亮的燈; B)隱藏任務, 要求在聽到一系列的數字之后在表盤上按順序點擊這些數字。

2.2.2 叢林記憶(Jungle Memory, JM)

叢林記憶(http://junglememory.com)為在線干預任務(T. Alloway, 2012; T. P. Alloway, Bibile, & Lau, 2013), 訓練語音回路和視空模板, 適用于7~16歲的兒童, 包括三個游戲, 游戲一針對視空模板, 如圖7-A所示, 字母在矩陣中呈現, 要求記住目標刺激的位置; 游戲二針對視空模板, 如圖7-B所示, 呈現兩個字母, 其中一個字母旋轉, 被試需要記住旋轉字母配對所旋轉的角度, 當一系列的字母呈現結束后, 需要按順序將這些字母的旋轉角度回憶出來; 游戲三針對語音回路, 要求解決難度逐漸增大的數學運算問題, 如圖7-C所示, 左側呈現運算問題, 右側呈現數字鍵, 受訓者在此輸入正確答案, 等題目呈現完畢,按順序回憶這些答案。該程序的難度有30個水平, 且訓練難度隨受訓者的表現而改變。

圖7 叢林記憶任務(Memosyne Ltd., http://junglememory.com)。A) 矩陣任務, 在矩陣中呈現字母, 要求記住目標刺激的位置; B)字母旋轉任務, 呈現兩個字母, 其中一個字母被旋轉, 要求記住其旋轉角度, 當一系列的字母呈現結束后, 按順序回憶這些字母的旋轉角度; C)計算廣度任務, 要求解決難度逐漸增大的數學運算問題。

表2 工作記憶的訓練任務

注：CWMS=Categorization Working Memory Span; OOO=Odd One Out; RM=Running Memory; JM=Jungle Memory

與數學能力有關的工作記憶訓練中常用多任務開展干預, 其中較為常見的訓練任務為CWMT和JM, 并且CWMT最被廣泛應用, 而另外幾個任務更多和其它工作記憶任務結合進行訓練。通過對以上任務(概括見表2)的簡單介紹, 可以更好理解訓練任務類型和訓練目標, 從而認識數學能力提高的機制。

3 工作記憶訓練對數學能力的提升作用

3.1 數學能力的多維結構

數學能力是一個多維的概念, 涉及包括數感、運算能力和數學推理能力等多個層面(Geary, 2006)。數感是心理表征和操作數字與數量的能力(Friso-van den Bos, Kroesbergen, & van Luit, 2014; Dehaene, 2001), 主要包括數數、數量區分、數軸估計等能力(Jordan, Kaplan, Ola′h, & Locuniak, 2006; Kroesbergen et al., 2012)。運算包括執行計算所需的事實和過程(Brainerd, 1983)。數學推理指對數量關系進行分析以解決問題的能力(Nunes, Bryant, Barros, & Sylva, 2012)。本綜述將首先針對以上三種數學能力的工作記憶訓練研究進行元分析, 之后再結合元分析結果分別詳細介紹三種數學能力的工作記憶訓練研究, 以了解工作記憶訓練對它們的作用機制。

3.2 工作記憶訓練對數學能力作用的元分析

3.2.1 研究方法

(1)文獻檢索與納入

在數據庫檢索平臺(PubMed, PsycINFO)對2000~2016年發表的文章進行檢索, 檢索關鍵詞working memory training和math*、arithmetic*、calculation*、number sense*、reason*的組合。另外, 為了避免遺漏文獻, 對當前幾篇綜述進行文獻回溯檢索(Melby-Lerv?g & Hulme, 2013; Peijnenborgh et al., 2016; Schwaighofer et al., 2015; Titz & Karbach, 2014)。具體檢索流程見圖8。文獻納入和排除標準為：干預類型為工作記憶訓練; 訓練效果中包含對數感、運算或數學推理能力的測量, 且在這些測試中可以抽取以上三種數學能力的相關數據以計算效應量; 文獻語言為英文; 僅納入已發表的文章。最終有23篇文獻納入元分析, 具體包括：數感的文獻4篇, 運算能力的文獻11篇, 數學推理能力的文獻10篇, 其中2篇文獻同時測量運算能力和數學推理能力。

(2) 調節變量的編碼

表3顯示調節變量的具體編碼。調節變量有助于解釋影響訓練效果的因素, 參照已有研究的編碼方式(Melby-Lerv?g & Hulme, 2013; Schwaighofer et al., 2015), 本文將各類調節變量進行如下編碼。

(3) 效應量計算

本研究采用Comprehensive Meta-Analysis (Borenstein, Hedges, Higgins, & Rothstein, 2005)進行元分析。采用Cohen’s作為效應量指標, 其中0.8為大效應量, 0.5為中等效應量, 0.2為小效應量。元分析采用隨機效應模型(random-effects model)。

3.2.2 工作記憶訓練對數感的效果

工作記憶的各個成分在數感任務中均發揮一定作用, 其中語音回路對于言語理解和獲得產生作用, 使兒童理解數感任務中對數字的口頭指導(Friso-van den Bos et al., 2014)。為正確執行數感任務, 數字表征需要與對應數量相聯系, 這種數量表征的空間映射與視空模板相關(Bachot, Gevers, Fias, & Roeyers, 2005; Herrera, Macizo, & Semenza, 2008; Kroesbergen et al., 2014); 并且特定策略的使用也需要視空模板的參與, 如手指數數的策略(Kytt?l?, Aunio, Lehto, Van Luit, & Hautam?ki, 2003)。中央執行系統在數感任務的提取和存儲過程發揮作用, 以數字比較為例, 對于兩個不同的數字, 需要使其與對應的數量匹配, 為更準確地執行任務, 這些信息需要被儲存起來, 中央執行系統的功能為幫助從長時記憶中提取這些信息, 執行任務時, 幫助整合與更新信息(Kroesbergen et al., 2014)。

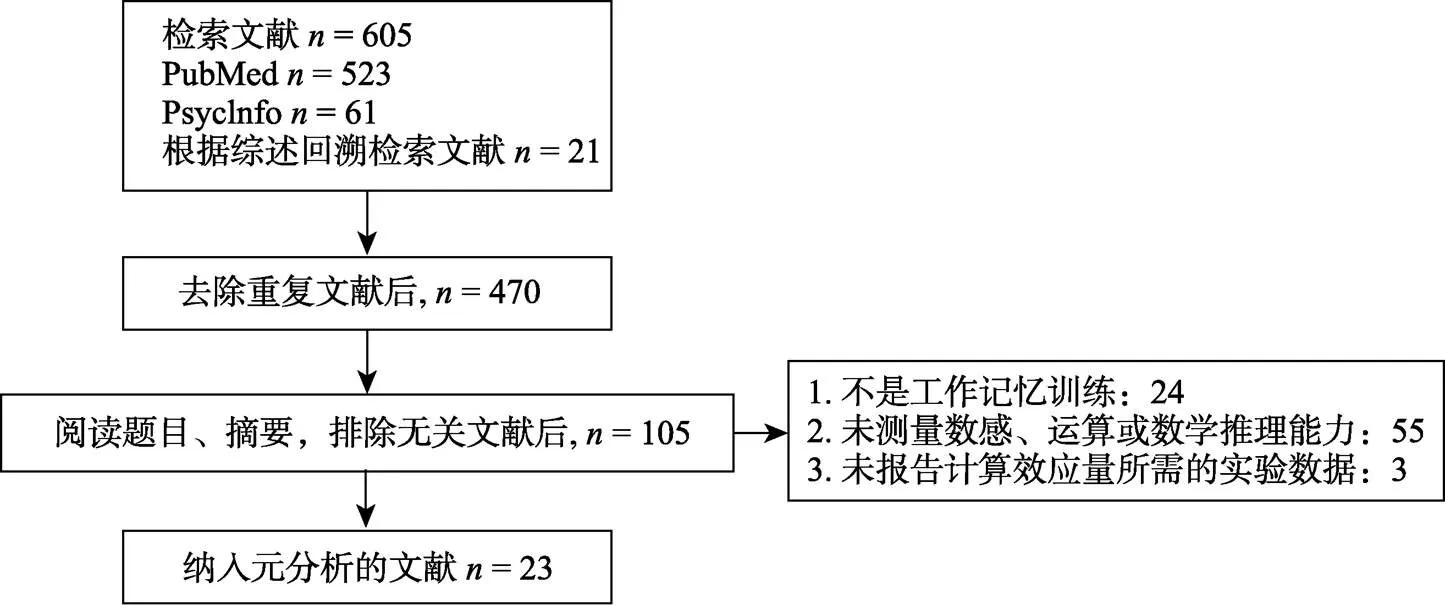
圖8 文獻檢索流程圖

表3 調節變量的編碼

由于工作記憶與數感之間存在的緊密聯系, 因此工作記憶訓練對數感能力的作用也受到研究者的關注。一些研究發現, 當進行工作記憶訓練時, 不論是正常兒童還是數感能力較低的兒童, 他們的數數、數量比較、數軸任務等成績都得到了提高(Kroesbergen et al., 2012, 2014; Passolunghi & Costa, 2016)。但是也有研究者對正常兒童進行數數和工作記憶結合進行訓練, 結果卻顯示進行這樣訓練的被試在數數任務上并沒有得到提高(Kytt?l? et al., 2015)。具體信息參考電子版附表1。

盡管如此, 研究更為一致的發現是工作記憶訓練對數感的改善可能是有效的, 并且在我們元分析的發現也驗證了這一點, 盡管研究數量相對有限, 我們發現數感的效應量為中等(Cohen’s= 0.51), 即工作記憶訓練可能有效改善數感能力(如表4所示)。同時, 我們也考察訓練強度等變量對數感能力改善效果的影響, 然而結果顯示這些因素均無法預測效應量的改變(如表5所示), 即這些因素對訓練效果的影響較小, 但由于研究數量相對有限, 這一結論需要更多研究驗證。

3.2.3 工作記憶訓練對運算能力的效果

已有研究表明, 工作記憶參與運算執行的過程中, 包括：工作記憶在運算的表征中發揮作用(Demir, Prado, & Booth, 2014; Rotzer et al., 2009), 比如對于水平呈現的題目人們傾向于使用語音回路進行言語表征, 垂直呈現的題目則使用視空模板進行視覺表征(Caviola, Mammarella, Cornoldi, & Lucangeli, 2012); 影響運算題目信息、中間結果(如29+34, 個位數上9+4=13, 需要將進位的中間結果保持, 并在十位數的運算中提取這個中間結果)及其它暫時信息的存儲 (張明, 陳騏, 2006); 影響策略的選擇與切換(Hubber, Gilmore, & Cragg, 2014; Wu et al., 2008; 陳英和, 王明怡, 2006; 王明怡, 陳英和, 2006); 抑制無關運算的進行與無關信息的干擾(Cragg & Gilmore, 2014; 陳英和, 耿柳娜, 2004)等等。

表4 工作記憶訓練對數學能力的作用

注：表示納入研究個數。**< 0.01.

表5 連續的調節變量對數感能力作用的影響

鑒于工作記憶在運算過程的重要作用, 因此很多研究者利用工作記憶設計針對運算能力的訓練。不少研究發現了工作記憶訓練能夠提高運算能力。例如, 對存在輕微智障的兒童進行視空模板任務的訓練, 結果發現他們在10周之后運算能力提高了(van der Molen et al., 2010)。此外, 對注意缺陷和數學困難的兒童(Nelwan & Kroesbergen, 2016)、患有工作記憶缺陷的兒童(Bergman-Nutley & Klingberg, 2014)或正常兒童(S?derqvist & Nutley, 2015)進行語音回路和視空模板的訓練, 訓練均提高了他們的運算表現。當在正常兒童中同時針對工作記憶三個成分進行訓練時, 結果發現他們在加法任務中的錯誤率更低(Witt, 2011)。在這些研究中, 不管是對工作記憶的單一成分, 還是同時對多個成分進行訓練, 都發現了訓練對于運算能力的積極作用。

但是, 也有很多研究并未驗證這個訓練的積極效應。有研究對成人進行語音回路或刷新能力的訓練, 在正常、注意缺陷多動障礙(Attention Deficit Hyperactivity Disorder, ADHD)或需要接受特殊教育的兒童中進行CWMT訓練, 均未能提高他們的運算能力(Dahlin, 2013; F?lth, Jaensson, & Johansson, 2015; Minear et al., 2016; Partanen, Jansson, Lisspers, & Sundin, 2015)。對工作記憶和數學困難的兒童用CWMT與刷新任務進行訓練, 結果發現這兩種訓練均無法提升障礙兒童的運算能力(Ang et al., 2015; Roberts et al., 2016)。有研究甚至對工作記憶的三個系統都進行訓練, 但仍然未獲有效提升(Kuhn & Holling, 2014)。具體信息參考電子版附表2。類似的, 我們元分析的結果也顯示工作記憶訓練無法遷移到運算能力, 其改善的效應量小, Cohen’s= 0.04, 這與過去的元分析的發現是一致的(Melby-Lerv?g, Redick, & Hulme, 2016; Peijnenborgh et al., 2016)。

由于分類調節變量樣本分布較為不均, 如表6所示, 所以本部分僅探究連續的調節變量的作用(見表7), 結果發現訓練頻率、訓練強度、每次訓練持續時間和訓練持續周數對訓練效果沒有影響, 已有研究也證實了這些因素對于遷移效果沒有作用, 研究者解釋可能是由于樣本數量太少, 數據統計力低(Melby-Lerv?g & Hulme, 2013; Schwaighofer et al., 2015)。

另外, 訓練方式的差異可能也會影響訓練效果, 比如Kuhn和Holling (2014)與Witt (2011)的研究, 前一項研究采用的是適應性訓練, 每天的訓練內容一樣, 但是任務難度會隨被試表現而改變, 訓練方式屬于核心訓練(core training), 即訓練目標是工作記憶的內在機制, 任務中需要運用工作記憶資源, 后一項研究中, 學生每周訓練的任務不同, 并且學習內容中涉及完成任務的策略, 不僅包括核心訓練, 還包括策略訓練(strategy training), 策略訓練指授予被試有效的編碼、保持和提取方法(Morrison & Chein, 2011), 因而后一項研究的訓練方式產生的效果更大。但由于在本研究中, 采用后一種訓練的研究很少, 因此無法對訓練方式進行編碼, 分析其作用, 未來還需要更多研究對此進行探討。

3.2.4 工作記憶訓練對數學推理能力的效果

大量研究已經探討工作記憶對一般推理能力的影響, 通過影響推理過程, 個體將題目信息維持在工作記憶中, 隨后利用這些信息確定各單元圖形的關系, 做出選擇(張清芳, 朱瀅, 2000)。研究發現工作記憶的不同成分在不同類型的推理任務中發揮作用各異, 比如視空模板可預測圖形推理能力的改善 (Stevenson, Heiser, & Resing, 2013)。通過訓練, 增大工作記憶容量, 或者提高使用策略與知識的效率, 便能夠提高推理能力。另外, 工作記憶與流體智力有重疊的腦區, 包括側前額皮層和頂葉皮層(Gray, Chabris, & Braver, 2003; Kane & Engle, 2002), 對這些重合的腦區進行訓練, 也能使推理能力得到提升。由于數學推理能力在一般推理能力、數能力(如運算)等能力的基礎上發展而來(Geary, 2006), 因此, 工作記憶訓練可能也能夠提高數學推理能力。

表6 分類調節變量對運算能力作用的影響

注：表示納入研究個數。

表7 連續的調節變量對運算能力作用的影響

然而, 現有的較少研究表明工作記憶訓練能夠提高數學推理能力。用聽力廣度任務對正常兒童進行訓練, 8次之后, 他們的數學推理能力提高了, 并且效果保持到3個月后(Cornoldi, Carretti, Drusi, & Tencati, 2015)。在異常兒童中, 如學習困難兒童或低工作記憶能力的兒童, 用JM或CWMT任務進行語音回路和視空模板的訓練, 也得到了積極的結果(Alloway, 2012; Holmes, Gathercole, & Dunning, 2009)。但是, 更多的研究發現這樣的訓練對數學推理能力沒有提升作用, 無論是正常(Harrison et al., 2013; Mansur-Alves & Flores- Mendoza, 2015; Redick et al., 2013; Rode, Robson, Purviance, Geary, & Mayr, 2014)還是異常(Alloway et al., 2013; Dunning et al., 2013; Phillips et al., 2016)個體都是如此。具體信息參考電子版附表3。

在本研究元分析的結果中, 同樣顯示工作記憶訓練無法改善數學推理能力, Cohen’s= ?0.06, 這與前人的發現一致(Melby-Lerv?g & Hulme, 2013)。這可能是因為很多研究的訓練目標主要集中在語音回路和視空模板, 而不是中央執行系統, 而過去有元分析表明刷新能力與數學表現之間存在著較強的聯系(Friso-van den Bos et al., 2013), 刷新訓練能夠改善一般推理能力(Au et al., 2015)。因此未來關于提升數學推理能力的研究應該更專注于利用中央執行系統的訓練。

進一步分析調節變量的作用, 發現多目標訓練效果可能差于單一目標訓練效果(見表8, 單一目標：Cohen’s= 0.07, 多目標：Cohen’s= ?0.24,= 0.060 )。這與已有研究結果不一致(Schwaighofer et al., 2015), 盡管對工作記憶多個系統進行訓練, 可以增加訓練和遷移情境之間的相似性, 但若是受訓者無法對各種混合情境進行正確辨認, 則可能會減弱它的作用, 甚至損害訓練的效果。研究還發現其它調節因素(如年齡段、被試類型等)均不影響訓練的遷移效果, 但也有一些研究卻發現10歲以上的兒童能夠在言語工作記憶上獲益更多, 但這一特點并沒有體現在數學推理能力上, 這可能是因為遷移到與工作記憶較為不一致的任務中, 其難度更大, 無法體現出年齡上的優勢(Peijnenborgh et al., 2015)。Titz和Karbach (2014)則認為低能力個體在工作記憶訓練中能獲益更多, 但我們的元分析并未驗證這一觀點。另外, 雖然研究中發現訓練任務類型和控制組類型對訓練效果沒有影響, 但是由于樣本差異較大, 需謹慎對待。最后, 訓練強度、訓練頻率和訓練持續時間對干預效果的影響(見表9)與已有研究的發現較為一致(Melby-Lerv?g & Hulme, 2013; Schwaighofer et al., 2015), 它們對于遠遷移的作用較為有限。訓練持續周數對數學推理能力也沒有影響, 這或許是因為對于數學推理能力的工作訓練持續時間較為接近, 變異性低, 因此無法體現它的作用。

綜上所述, 工作記憶訓練對數感可能具有改善作用, 效應量為中等(Cohen’s= 0.51), 而在運算和數學推理能力中工作記憶訓練則無積極作用。此外, 訓練目標會影響數學能力的改善效果。但值得注意的是, 由于研究數量的有限, 對這些分析所得出的結論需謹慎看待, 未來還需要更多的研究來探討這些變量的作用。

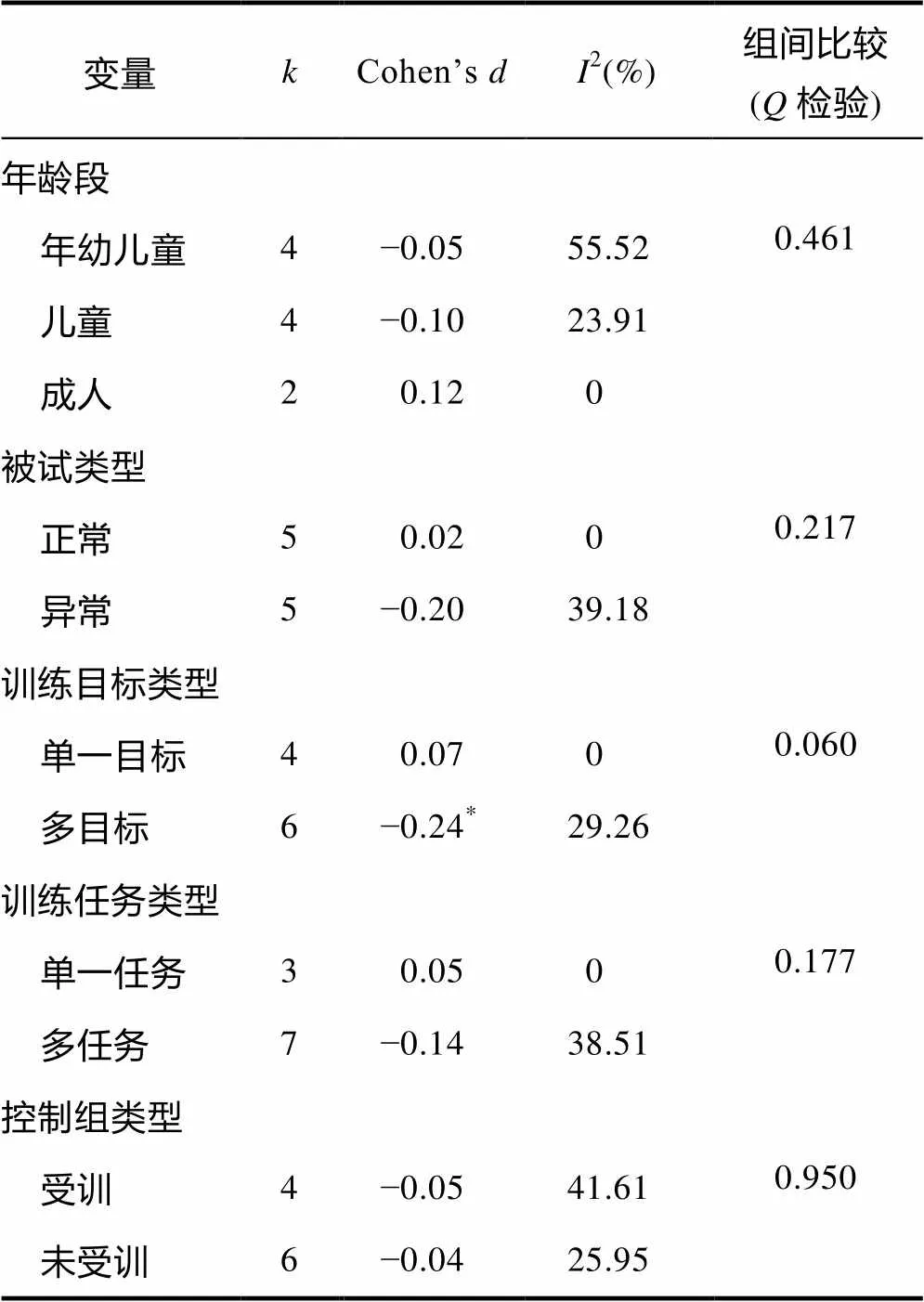
表8 分類調節變量對數學推理能力作用的影響

注：表示納入研究個數。*< 0.05.

表9 連續的調節變量對數學推理能力作用的影響

盡管本研究發現工作記憶訓練可能對數感具有改善作用, 但是數感能力為什么得到提升的背后機制還不是非常清楚, 值得深入探討。另外, 鑒于導致數學障礙的原因之一是數感能力的缺陷, 因此是否能夠通過工作記憶訓練改善數感能力, 從而對數學障礙有所緩解, 這也是值得進一步探討的方向。

本研究發現了訓練任務所針對的目標會影響訓練效果, 但是依然存在很多問題需要進一步探討, 比如, 訓練方法的有效性, 訓練任務是否準確觸及了所針對的工作記憶能力？不同目標的訓練方式對于提高數學能力究竟存在哪些不同影響。由于過去的研究很多都采用多維度任務進行訓練, 因此我們很難判斷究竟哪些訓練更為有效, 或者完全無關哪個訓練任務, 而是取決于不同訓練任務疊加訓練效應。這些問題同樣需要今后大量的實證研究進行探討。

(*為納入元分析文獻)

陳英和, 耿柳娜. (2004). 工作記憶與算術認知的研究現狀與前瞻.(1), 40–44.

陳英和, 王明怡. (2006). 工作記憶廣度對兒童算術認知策略的影響.(2), 29–35.

黎翠紅, 何旭, 郭春彥. (2014). 工作記憶訓練的研究述評.(3), 407–412.

劉春雷, 周仁來. (2012). 工作記憶訓練對認知功能和大腦神經系統的影響.(7), 1003–1011.

王明怡, 陳英和. (2006). 工作記憶中央執行對兒童算術認知策略的影響.(4), 24–28.

張明, 陳騏. (2006). 工作記憶子成分在聽覺障礙兒童心算過程中的作用.(1), 76–79.

張清芳, 朱瀅. (2000). 工作記憶和推理.(1), 12–17.

趙鑫, 王一雪, 劉丹瑋, 周仁來. (2011). 工作記憶刷新訓練對兒童流體智力的影響.(17), 1345–1348.

*Alloway, T. (2012). Can interactive working memory training improve learning.(3), 197–207.

Alloway, T. P., & Alloway, R. G. (2008).. Edinburgh, United Kingdom: Memosyne.

Alloway, T. P., Gathercole, S. E., Kirkwood, H., & Elliott, J. (2008). Evaluating the validity of the Automated Working Memory Assessment.(7), 725–734.

*Alloway, T. P., Bibile, V., & Lau, G. (2013). Computerized working memory training: Can it lead to gains in cognitive skills in students?(3), 632–638.

*Ang, S. Y., Lee, K., Cheam, F., Poon, K., & Koh, J. (2015). Updating and working memory training: Immediate improvement, long-term maintenance, and generalisability to non-trained tasks.(2), 121–128.

Au, J., Sheehan, E., Tsai, N., Duncan, G. J., Buschkuehl, M., & Jaeggi, S. M. (2015). Improving fluid intelligence with training on working memory: A meta-analysis.(2), 366–377.

Bachot, J., Gevers, W., Fias, W., & Roeyers, H. (2005). Number sense in children with visuospatial disabilities: Orientation of the mental number line., 172–183.

*Bergman-Nutley, S., & Klingberg, T. (2014). Effect of working memory training on working memory, arithmetic and following instructions.(6), 869–877.

Borella, E., Carretti, B., Cornoldi, C., & De Beni, R. (2007). Working memory, control of interference and everyday experience of thought interference: When age makes the difference.(3), 200–206.

Borella, E., Carretti, B., & De Beni, R. (2008). Working memory and inhibition across the adult life-span.(1), 33–44.

Borella, E., Carretti, B., Riboldi, F., & De Beni, R. (2010). Working memory training in older adults: Evidence of transfer and maintenance effects.(4), 767–778.

Borenstein, M., Hedges, L., Higgins, J., & Rothstein, H. (2005).(Version 2) [Software]. Engelwood, NJ: Biostat.

Brainerd, C. J. (1983). Young children's mental arithmetic errors: A working-memory analysis.(4), 812–830.

Carretti, B., Cornoldi, C., De Beni, R., & Palladino, P. (2004). What happens to information to be suppressed in working-memory tasks? Short and long term effects.(6), 1059–1084.

Caviola, S., Mammarella, I. C., Cornoldi, C., & Lucangeli, D. (2012). The involvement of working memory in children's exact and approximate mental addition.(2), 141–160.

*Cornoldi, C., Carretti, B., Drusi, S., & Tencati, C. (2015). Improving problem solving in primary school students: The effect of a training programme focusing on metacognition and working memory.(3), 424–439.

Cragg, L., & Gilmore, C. (2014). Skills underlying mathematics: The role of executive function in the development of mathematics proficiency.(2), 63–68.

*Dahlin, K. I. E. (2013). Working memory training and the effect on mathematical achievement in children with attention deficits and special needs.(1), 118–133.

Dehaene, S. (2001). Précis of the number sense.(1), 16–36.

Demir, ?. E., Prado, J., & Booth, J. R. (2014). The differential role of verbal and spatial working memory in the neural basis of arithmetic.(6), 440–458.

*Dunning, D. L., Holmes, J., & Gathercole, S. E. (2013). Does working memory training lead to generalized improvements in children with low working memory? A randomized controlled trial.(6), 915–925.

*F?lth, L., Jaensson, L., & Johansson, K. (2015). Working memory training – A Cogmed intervation.(2), 28–35.

Friso-van den Bos, I., Kroesbergen, E. H., & van Luit, J. E. H. (2014). Number sense in kindergarten children: Factor structure and working memory predictors., 23–29.

Friso-van den Bos, I., van der Ven, S. H. G., Kroesbergen, E. H., & van Luit, J. E. H. (2013). Working memory and mathematics in primary school children: A meta-analysis., 29–44.

Geary, D. C. (2006). Development of mathematical understanding. In W. Damon, R. M. Lerner, D. Kuhn, & R. S. Sielger (Eds.),(6th ed., pp.777– 810). New York: Wiley.

Giofrè, D., Mammarella, I. C., & Cornoldi, C. (2013). The structure of working memory and how it relates to intelligence in children.(5), 396–406.

Gray, J. R., Chabris, C. F., & Braver, T. S. (2003). Neural mechanisms of general fluid intelligence.(3), 316–322.

Harrison, T. L., Shipstead, Z., Hicks, K. L., Hambrick, D. Z., Redick, T. S., & Engle, R. W. (2013). Working memory training may increase working memory capacity but not fluid intelligence.(12), 2409–2419.

Henry, L. A. (2001). How does the severity of a learning disability affect working memory performance?(4–6), 233–247.

Herrera, A., Macizo, P., & Semenza, C. (2008). The role of working memory in the association between number magnitude and space.(2), 225–237.

Hitch, G. J., & McAuley, E. (1991). Working memory in children with specific arithmetical learning difficulties.(3), 375–386.

*Holmes, J., Gathercole, S. E., & Dunning, D. L. (2009). Adaptive training leads to sustained enhancement of poor working memory in children.(4), F9–F15.

Hubber, P. J., Gilmore, C., & Cragg, L. (2014). The roles of the central executive and visuospatial storage in mental arithmetic: A comparison across strategies.(5), 936–954.

Jaeggi, S. M., Buschkuehl, M., Jonides, J., & Perrig, W. J. (2008). Improving fluid intelligence with training on working memory.(19), 6829– 6833.

Jaeggi, S. M., Buschkuehl, M., Jonides, J., & Shah, P. (2011). Short- and long-term benefits of cognitive training.(25), 10081–10086.

Jahanshahi, M., Saleem, T., Ho, A. K, Fuller, R., & Dirnberger, G. (2008). A preliminary investigation of the running digit span as a test of working memory.(1–2), 17–25.

Jordan, N. C., Kaplan, D., Ola′h, L. N., & Locuniak, M. N. (2006). Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties.(1), 153–175.

Kane, M. J., & Engle, R. W. (2002). The role of prefrontal cortex in working-memory capacity, executive attention, and general fluid intelligence: An individual-differences perspective.(4), 637–671.

Klingberg, T., Fernell, E., Olesen, P., J., Johnson, M., Gustafsson, P., Dahlstr?m, K., … Westerberg, H. (2005). Computerized training of working memory in children with ADHD: A randomized, controlled trial.(2), 177–186

Krichner, W. K. (1958). Age differences in short-term retention of rapidly changing information.(4), 352–358.

*Kroesbergen, E. H., Van't Noordende, J. E., & Kolkman, M. E. (2012). Number sense in low-performing kindergarten children: Effects of a working memory and an early math training. In: Z. Breznitz, O. Rubinsten, V. Molfese, & D. Molfese (Eds.),(pp. 295–313). Netherlands: Springer.

*Kroesbergen, E. H., Van't Noordende, J. E., & Kolkman, M. E. (2014). Training working memory in kindergarten children: Effects on working memory and early numeracy.(1), 23–37.

Kuhn, J.-T., & Holling, H. (2014). Number sense or working memory? The effect of two computer-based trainings on mathematical skills in elementary school.(2), 59–67.

Kytt?l?, M., Aunio, P., Lehto, J. E., Van Luit, J., & Hautam?ki, J. (2003). Visuospatial working memory and early numeracy.(3), 65–76.

*Kytt?l?, M., Kanerva, K., & Kroesbergen, E. (2015). Training counting skills and working memory in preschool.(4), 363–370.

*Mansur-Alves, M., & Flores-Mendoza, C. (2015). Working memory training does not improve intelligence: Evidence from Brazilian children.(3), 474–482.

Melby-Lerv?g, M., & Hulme, C. (2013). Is working memory training effective? A meta-analytic review.(2), 270–291.

Melby-Lerv?g, M., Redick, T. S., & Hulme, C. (2016). Working memory training does not improve performance on measures of intelligence or other measures of "far transfer": Evidence from a meta-analytic review.(4), 512–534.

*Minear, M., Brasher, F., Guerrero, C. B., Brasher, M., Moore, A., & Sukeena, J. (2016). A simultaneous examination of two forms of working memory training: Evidence for near transfer only.(7), 1014–1037.

Morrison, A. B., & Chein, J. M. (2011). Does working memory training work? The promise and challenges of enhancing cognition by training working memory.(1), 46–60.

*Nelwan, M., & Kroesbergen, E. H. (2016). Limited near and far transfer effects of Jungle Memory working memory training on learning mathematics in children with attentional and mathematical difficulties., 1384.

Nunes, T., Bryant, P., Barros, R., & Sylva, K. (2012). The relative importance of two different mathematical abilities to mathematical achievement., 136–156.

*Partanen, P., Jansson, B., Lisspers, J., & Sundin, ?. (2015). Metacognitive strategy training adds to the effects of working memory training in children with special educational needs.(3), 130–140.

*Passolunghi, M. C., & Costa, H. M. (2016). Working memory and early numeracy training in preschool children.(1), 81–98.

Peijnenborgh, J. C., Hurks, P. M., Aldenkamp, A. P., Vles, J. S.., & Hendriksen, J. G. M. (2016). Efficacy of working memory training in children and adolescents with learning disabilities: A review study and meta-analysis.(5–6), 645–672.

Phillips, N. L., Mandalis, A., Benson, S., Parry, L., Epps, A., Morrow, A., & Lah, S. (2016). Computerized working memory training for children with moderate to severe traumatic brain injury: A double-blind, randomized, placebo-controlled trial.(23), 2097–2104.

Pollack, I., Johnson, L. B., & Knaff, P. R. (1959). Running memory span.(3), 137–146.

Raghubar, K. P., Barnes, M. A., & Hecht, S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches.(2), 110–122.

*Redick, T. S., Shipstead, Z., Harrison, T. L., Hicks, K. L., Fried, D. E., Hambrick, D. Z., ... Engle, R. W. (2013). No evidence of intelligence improvement after working memory training: A randomized, placebo-controlled study.(2), 359–379.

*Roberts, G., Quach, J., Spencer-Smith, M., Anderson, P. J., Gathercole, S., Gold, L., ... Wake, M. (2016). Academic outcomes 2 years after working memory training for children with low working memory: A randomized clinical trial.(5), e154568.

*Rode, C., Robson, R., Purviance, A., Geary, D. C., & Mayr, U. (2014). Is working memory training effective? A study in a school setting.(8), e104796.

Rotzer, S., Loenneker, T., Kucian, K., Martin, E., Klaver, P., & von Aster, M. (2009). Dysfunctional neural network of spatial working memory contributes to developmental dyscalculia.(13), 2859–2865.

*S?derqvist, S., & Nutley, S. B. (2015). Working memory training is associated with long term attainments in math and reading., 1711.

Schwaighofer, M., Fischer, F., & Bühner, M. (2015). Does working memory training transfer? A meta-analysis including training conditions as moderators.(2), 138–166.

Stevenson, C. E., Heiser, W. J., & Resing, W. C. M. (2013). Working memory as a moderator of training and transfer of analogical reasoning in children.(3), 159–169.

Titz, C., & Karbach, J. (2014). Working memory and executive functions: Effects of training on academic achievement., 852–868.

*van der Molen, M. J., van Luit, J. E., van der Molen, M. W., Klugkist, I., & Jongmans, M. J. (2010). Effectiveness of a computerised working memory training in adolescents with mild to borderline intellectual disabilities.(5), 433–447.

von Bastian, C. C., Langer, N., J?ncke, L., & Oberauer, K. (2013). Effects of working memory training in young and old adults.(4), 611–624.

*Witt, M. (2011). School based working memory training: Preliminary finding of improvement in children's mathematical performance., 7–15.

Wu, S. S., Meyer, M. L., Maeda, U., Salimpoor, V., Tomiyama, S., Geary, D. C., & Menon, V. (2008). Standardized assessment of strategy use and working memory in early mental arithmetic performance.(3), 365–393.

附錄：

附表1 工作記憶訓練對數感影響的研究總結列表

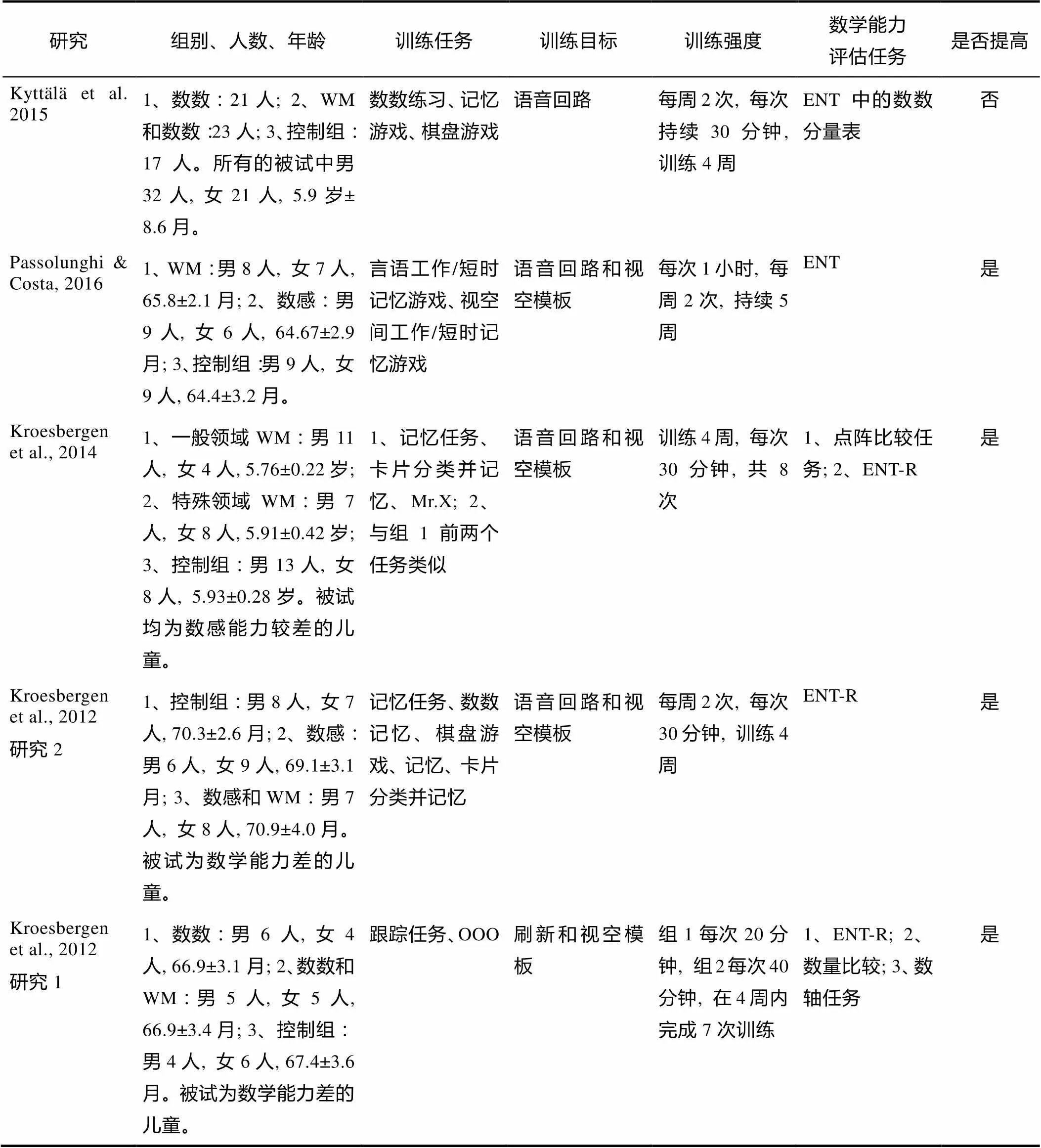
研究組別、人數、年齡訓練任務訓練目標訓練強度數學能力評估任務是否提高 Kytt?l? et al. 20151、數數：21人; 2、WM和數數：23人; 3、控制組：17人。所有的被試中男32人, 女21人, 5.9歲± 8.6月。數數練習、記憶游戲、棋盤游戲語音回路每周2次, 每次持續30分鐘, 訓練4周ENT中的數數分量表否 Passolunghi & Costa, 20161、WM：男8人, 女7人, 65.8±2.1月; 2、數感：男9人, 女6人, 64.67±2.9月; 3、控制組：男9人, 女9人, 64.4±3.2月。言語工作/短時記憶游戲、視空間工作/短時記憶游戲語音回路和視空模板每次1小時, 每周2次, 持續5周ENT是 Kroesbergen et al., 20141、一般領域WM：男11人, 女4人, 5.76±0.22歲; 2、特殊領域WM：男7人, 女8人, 5.91±0.42歲; 3、控制組：男13人, 女8人, 5.93±0.28歲。被試均為數感能力較差的兒童。1、記憶任務、卡片分類并記憶、Mr.X; 2、與組1前兩個任務類似語音回路和視空模板訓練4周, 每次30分鐘, 共8 次1、點陣比較任務; 2、ENT-R是 Kroesbergen et al., 2012研究21、控制組：男8人, 女7人, 70.3±2.6月; 2、數感：男6人, 女9人, 69.1±3.1月; 3、數感和WM：男7人, 女8人, 70.9±4.0月。被試為數學能力差的兒童。記憶任務、數數記憶、棋盤游戲、記憶、卡片分類并記憶語音回路和視空模板每周2次, 每次30分鐘, 訓練4周ENT-R 是 Kroesbergen et al., 2012研究11、數數：男6人, 女4人, 66.9±3.1月; 2、數數和WM：男5人, 女5人, 66.9±3.4月; 3、控制組：男4人, 女6人, 67.4±3.6月。被試為數學能力差的兒童。跟蹤任務、OOO刷新和視空模板組1每次20分鐘, 組2每次40分鐘, 在4周內完成7次訓練1、ENT-R; 2、數量比較; 3、數軸任務是

注：WM=Working Memory; ENT= Early Numeracy Test; ENT-R= Early Numeracy Test-Revised; OOO=Odd One Out. 以上研究未探討訓練后效

附表2 工作記憶訓練對運算能力影響的研究總結列表

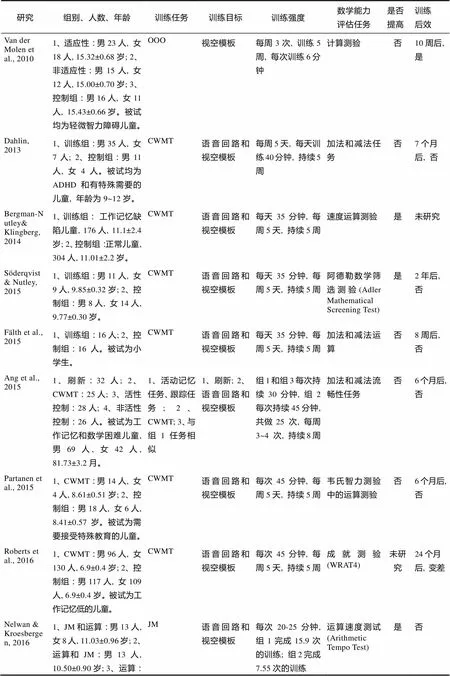
研究組別、人數、年齡訓練任務訓練目標訓練強度數學能力評估任務是否提高訓練后效 Van der Molen et al., 20101、適應性：男23人, 女18人, 15.32±0.68歲; 2、非適應性：男15人, 女12人, 15.00±0.70歲; 3、控制組：男16人, 女11人, 15.43±0.66歲。被試均為輕微智力障礙兒童。OOO視空模板每周3次, 訓練5周, 每次訓練6分鐘計算測驗否10周后, 是 Dahlin, 20131、訓練組：男35人, 女7人; 2、控制組：男11人, 女4人。被試均為ADHD和有特殊需要的兒童, 年齡為9~12歲。CWMT語音回路和視空模板每周5天, 每天訓練40分鐘, 持續5周加法和減法任務否7個月后, 否 Bergman-Nutley& Klingberg, 20141、訓練組：工作記憶缺陷兒童, 176人, 11.1±2.4歲; 2、控制組：正常兒童, 304人, 11.01±2.2歲。CWMT語音回路和視空模板每天35分鐘, 每周5天, 持續5周速度運算測驗是未研究 S?derqvist & Nutley, 20151、訓練組：男11人, 女9人, 9.85±0.32歲; 2、控制組：男8人, 女14人, 9.77±0.30歲。CWMT語音回路和視空模板每天35分鐘, 每周5天, 持續5周阿德勒數學篩選測驗(Adler Mathematical Screening Test)是2年后, 否 F?lthet al., 20151、訓練組：16人; 2、控制組：16人。被試為小學生。CWMT語音回路和視空模板每天35分鐘, 每周5天, 持續5周加法和減法運算否8周后, 否 Ang et al., 20151、刷新：32人; 2、CWMT：25人; 3、活性控制：28人; 4、非活性控制：26人。被試為工作記憶和數學困難兒童, 男69人, 女42人, 81.73±3.2月。1、活動記憶任務、跟蹤任務; 2、CWMT; 3、與組1任務相似1、刷新; 2、語音回路和視空模板組1和組3每次持續30分鐘, 組2每次持續45分鐘, 共做25 次, 每周3~4 次, 持續8周加法和減法流暢性任務否6個月后, 否 Partanen et al., 20151、CWMT：男14人, 女4人, 8.61±0.51歲; 2、控制組：男18人, 女6人, 8.41±0.57歲。被試為需要接受特殊教育的兒童。CWMT語音回路和視空模板每次45分鐘, 每周5天, 持續5周韋氏智力測驗中的運算測驗否6個月后, 否 Roberts et al., 20161、CWMT：男96人, 女130人, 6.9±0.4歲; 2、控制組：男117人, 女109人, 6.9±0.4歲。被試為工作記憶低的兒童。CWMT語音回路和視空模板每次45分鐘, 每周5天, 持續5周成就測驗(WRAT4)未研究24個月后, 變差 Nelwan & Kroesbergen, 20161、JM和運算：男13人, 女8人, 11.03±0.96歲; 2、運算和JM：男13人, 10.50±0.90歲; 3、運算：男15人, 女4人, 10.86±1.00歲。被試為注意和數學困難的兒童。JM語音回路和視空模板每次20-25分鐘, 組1完成15.9次的訓練; 組2完成7.55次的訓練運算速度測試(Arithmetic Tempo Test)是否

續表2

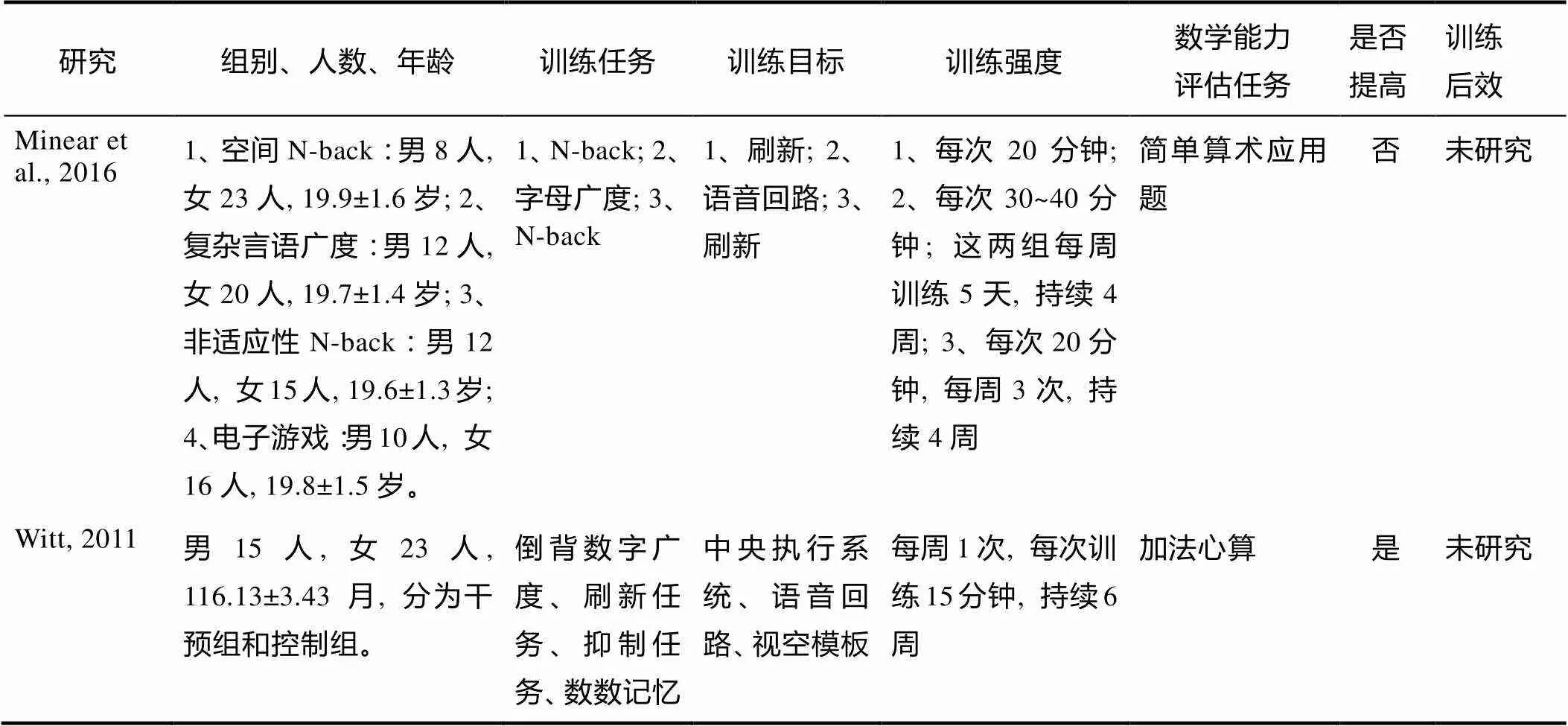
研究組別、人數、年齡訓練任務訓練目標訓練強度數學能力評估任務是否提高訓練后效 Minear et al., 20161、空間N-back：男8人, 女23人, 19.9±1.6歲; 2、復雜言語廣度：男12人, 女20人, 19.7±1.4歲; 3、非適應性N-back：男12人, 女15人, 19.6±1.3歲; 4、電子游戲：男10人, 女16人, 19.8±1.5歲。1、N-back; 2、字母廣度; 3、N-back1、刷新; 2、語音回路; 3、刷新1、每次20分鐘; 2、每次30~40分鐘; 這兩組每周訓練5天, 持續4周; 3、每次20分鐘, 每周3次, 持續4周簡單算術應用題否未研究 Witt, 2011男15人, 女23人, 116.13±3.43月, 分為干預組和控制組。倒背數字廣度、刷新任務、抑制任務、數數記憶中央執行系統、語音回路、視空模板每周1次, 每次訓練15分鐘, 持續6周加法心算是未研究

注：OOO=Odd One Out; ADHD=Attention Deficit Hyperactivity Disorder; CWMT=Cogmed Working Memory Training; WRAT4=Wide Range Achievement Test-4th ed; JM=Jungle Memory

附表3 工作記憶訓練對推理能力影響的研究總結列表

研究組別、人數、年齡、訓練任務訓練目標訓練強度數學能力評估任務是否提高訓練后效 Cornoldi et al., 20151、組一：男33人, 女36人, 9.0±0.9歲; 2、組二：男31人, 女33人, 9.3±0.7歲。前三個月, 組一訓練, 組二不訓練, 后三個月則相反。聽力廣度語音回路每周1次, 每次持續1小時, 總共8 次AC-MT 是3個月后, 是 Rode et al., 20141、WM訓練：156人; 2、控制組：126人。被試為三年級的學生。運算廣度語音回路每次20~30分鐘, 每周5次, 持續訓練4周韋氏個人成就測驗中的數學推理量表否未研究 Redick et al., 20131、適應性雙N-back：男10人, 女14人, 21.1±2.7歲; 2、視覺搜索：男12人, 女17人, 20.7±2.5歲; 3、控制組：男10人, 女10人, 21.2±2.5歲。雙N-back 刷新每次完成20 組, 時間30~40分鐘, 訓練20 次, 平均訓練46天數字排列任務否未研究 Mansur-Alves & Flores- Mendoza, 20151、控制組：26人; 2、WM訓練：27人。男22人, 女31人, 年齡11.17±0.37歲。數字排序任務、語法ABC任務、字母順序任務語音回路每次50分鐘, 每周2次, 持續8周BPR5-NR 否未研究 Dunning et al., 20131、適應性：男8人, 女7人, 9歲3月±4.97月; 2、非適應性：男8人, 女11人, 9歲6月±7.15月; 3、控制組：男31人, 女29人。被試為工作記憶低的兒童, 8歲5月±7.79月。1、CWMT; 2、評估版本的CWMT語音回路和視空模板共有20-25 次, 每次需30-45分鐘, 訓練6周WOND否1年后, 否 Holmes et al., 20091、適應性：男12人, 女10人, 10歲1月; 2、非適應性：男15人, 女5人, 9歲9月。被試均為工作記憶低的兒童。CWMT 語音回路和視空模板每周訓練5天, 每次35分鐘, 訓練5~7周, 至少訓練20天WOND否6個月后, 是

續表3

注：AC-MT=Assessment of arithmetic and problem solving skills; WM=Working Memory; BPR5-NR=Brazilian Cognitive Reasoning Battery-Numerical Reasoning; CWMT=Cogmed Working Memory Training; WOND=Wechsler Objective Numerical Dimension; JM=Jungle Memory

Enhancing mathematical abilities: A meta-analysis on the effect of working memory training

GUO Liyue; YAN Chao; DENG Ciping

(School of Psychology and Cognitive Science, East China Normal University, Shanghai 200062, China)

Working memory training can effectively improve individual’s cognitive performance. In last decades, accumulating studies examined the transfer effects of working memory training on the mathematical abilities. However, findings from these studies render inconsistent depending on the measure of mathematical abilities, types of working memory training, and participants. In this meta-analysis, we thus reviewed two types of trainings strategies–uni-dimensional and multi-dimensional trainings – and their effects on the enhancement of mathematical skills, including number sense, arithmetic and mathematics reasoning. Results showed that working memory training significantly improved number sense with a medium effect size (Cohen’s= 0.51), rather than arithmetic (Cohen’s= 0.04) and mathematics reasoning (Cohen’s=-0.06). Furthermore, the types of working memory training significantly moderated the transfer effects of working memory training on mathematical performance.

working memory training; mathematical ability; number sense; arithmetic; mathematical reasoning

B849:G44

2017-07-10

* 國家自然科學基金面上項目(項目編號71373081); 國家自然科學基金青年項目(項目編號31500894)。

嚴超, E-mail: cyan@psy.ecnu.edu.cn; 鄧賜平, E-mail: cpdeng@psy.ecnu.edu.cn

10.3724/SP.J.1042.2018.01576