基于特征價格理論和神經網絡的武漢二手房價自動評估
陳敏,李英冰
(1.武漢大學測繪學院,湖北 武漢 430079; 2.武漢大學測繪學院時空大數據研究中心,湖北 武漢 430079)
1 引 言
在房地產稅制改革和大數據的背景下,我國的房地產評估行業面臨新的挑戰[1]。許軍等指出我國房地產評估行業的目標應由“以房為本”、“服務開發”的模式轉變為“以人為本”、“服務兩端”的模式[2]。“以人為本”要求從消費者需求的角度出發考察影響房價的因素,將其作為房價評估依據;“服務兩端”強調建立統一管理平臺,為消費者和政府相關部門提供經濟、高效的優質信息服務。
目前,國外已經有了基于CAMA (Computer Assisted Mass Appraisal)和GIS(Geography Information System)的房地產批量評估方法,而我國仍處于大數據系統的構建階段[2],缺少相關的技術、算法支持。特征價格理論認為住宅價格的確定不是基于作為整體的住宅本身,而等于住宅各個屬性的效用總和[3],呼應了“以人為本”的需求;人工神經網絡作為一個強大的非線性變換系統[4],具有自組織、自學習的特點,能夠充分利用大數據優勢,在實例研究中顯現出較傳統方法更高的準確率和效率[5~9],或許能在自動批量評估系統中發揮重要作用。因此,綜合特征價格理論和人工神經網絡,探索更準確、效率更高的估價算法,能夠提高估價方法的科學性和前瞻性,并推動統一的房地產信息服務平臺的構建。
2 數據處理與模型構建
2.1 研究區域
如圖1所示,研究區域為距離武漢市政府 15 km的武昌、江漢、洪山、青山、江岸、硚口、漢陽七個行政區內的212個小區。各小區與市中心聯系緊密,基本在三環線內。各小區平均二手房價格 3 714 元/m2~22 112 元/m2不等,小區內不同房屋成交價也有差別。
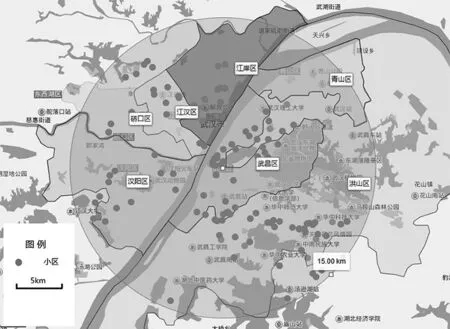
圖1 研究區域及小區分布
2.2 基于特征價格理論的樣本數據整理
特征價格模型的一般形式[4]為:
P=f(X1,X2,…,Xi)
(1)
其中P為住宅價格,Xi表示住宅特征,f為特征與價格之間的函數關系。
住宅特征(即房價影響因子)的選取十分重要,特征價格理論默認模型僅包含影響房價且量測精確的因素。但是,影響房價的因素十分復雜,且存在隨機波動;加上某些特征不能做到精確測量和量化,實際難以達到這一標準。
王娟娟等[10]統計了相關文獻中常用的特征變量及其顯著性,為特征變量的選取提供了參考。根據此參考及數據庫數據,結合武漢市房地產市場特點,確定了參與評估的14個特征變量,如表1所示。

特征變量及數據來源 表1
量化數據時定量特征直接引用數值;定性特征則采用二元虛擬變量法、李克特量表法或綜合性指標法量化[11]。再手動補充、剔除缺失值、刪除虛假數據、剔除異常值,最終得到武漢市二手房數目多于200套的住宅小區212個,小區內部二手房樣本 84 215條。
2.3 人工神經網絡分級模型搭建
利用神經網絡估計住宅價格,思路是把住宅的各個特征變量作為輸入,房價作為輸出,把各個特征變量與房價之間的關系模擬為各層神經元之間連接的權值與閾值。通過大量樣本的監督學習,得到合適的權值與閾值,即確定了特征變量與房價之間的關系。
部分利用神經網絡進行估價的研究采用的訓練樣本體積偏小,并且只給出一個通用網絡模型,沒有考慮空間異質性對模型精度的影響,如周圍是否有學校很大程度影響到購房決策[12]。不考慮小區間這類影響因子的差異,模型的泛化能力無法得到保證,難以應用于實際。考慮到隨著樣本體積增大,網絡訓練的速度降低,效率不高[13],本文設計了整體基準價和精確估價的兩級模型,結構如圖2所示。抽取研究區域的樣本訓練得到基準價網絡,再輸入需要估價的小區樣本進一步訓練得到適合該小區的精確估價網絡,希望在保證模型的泛化能力同時提高估價效率。
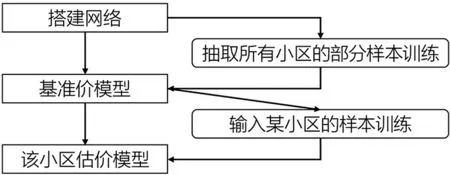
圖2 分級模型結構
基準價模型和精確估價模型的構建涉及網絡結構、激活函數確定,訓練算法選擇的工作。其中,隱層節點個數、激活函數以及學習速率可以基于經驗和試湊法確定,通過隨機抽取5 000條樣本進行實驗,不斷調整學習速率,確定最優隱層節點數為30,激活函數第一層為logsig,第二層tansig。網絡的訓練采用反向傳播的思想。對每一個樣本(x,y),(x為特征向量,y為價格)先進行前向傳遞,求每個神經元的激活值a,得到估價h(x)。
a=∑σ(ωx+b)
(2)
再比較h(x)與真實價格,利用損失函數求損失C(函數cost通常是均方誤差)。
C=cost[h(x),y]
(3)
接著進行誤差反向傳播,從最后一層向前依次求各層誤差(鏈式法則),并調整權值和偏置(式(4)、式(5)運用的學習算法是梯度下降)。反復迭代至C足夠小,停止訓練。
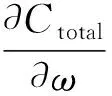
(4)
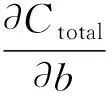
(5)
反向傳播有梯度下降法、擬牛頓法、共軛梯度法和Levenberg-Marquardt法等經典算法。不同訓練算法最小化損失函數的思想不同,在收斂速度、計算量、泛化能力上存在差異,因而針對不同參數規模的網絡應選取不同的訓練算法[14]。

圖3 網絡結構及訓練思路
本文影響因子數較少(14),網絡參數不多(481),但樣本體積較大(84 215)。 圖3展示了網絡結構和訓練思路,為確定最優訓練算法,抽出“武漢天地御江璟城”小區數據,將其余 83 871條樣本分為訓練組(80 000條)和測試組(3 871條)輸入網絡用不同算法分別訓練,綜合比較模型訓練時間、估價結果精度(如表2所示)得到合適的訓練算法。
3 結果及分析
模型評價采取擬合優度R2和估價相對誤差RE、絕對誤差AE。擬合優度評價模型對觀測值的擬合程度,越接近1效果越好;相對誤差與絕對誤差能更直觀地表現估價精度。
R2=(TSS-RSS)/TSS
(6)
AE=h(x)-y
(7)
RE=AE/y
(8)
其中,TSS為總誤差平方和,RSS為殘差平方和。
用不同訓練算法訓練基準價網絡得到估價結果,如表2所示,比較結果的擬合優度、平均相對誤差、相對誤差在10%、20%內的樣本比例,梯度下降法和共軛梯度法均陷入了局部最優解,模型精度低;擬牛頓法精度雖高但不及L-M法,且訓練時間過長;L-M法估價精度高、收斂速度快,訓練時間適中,最合適。
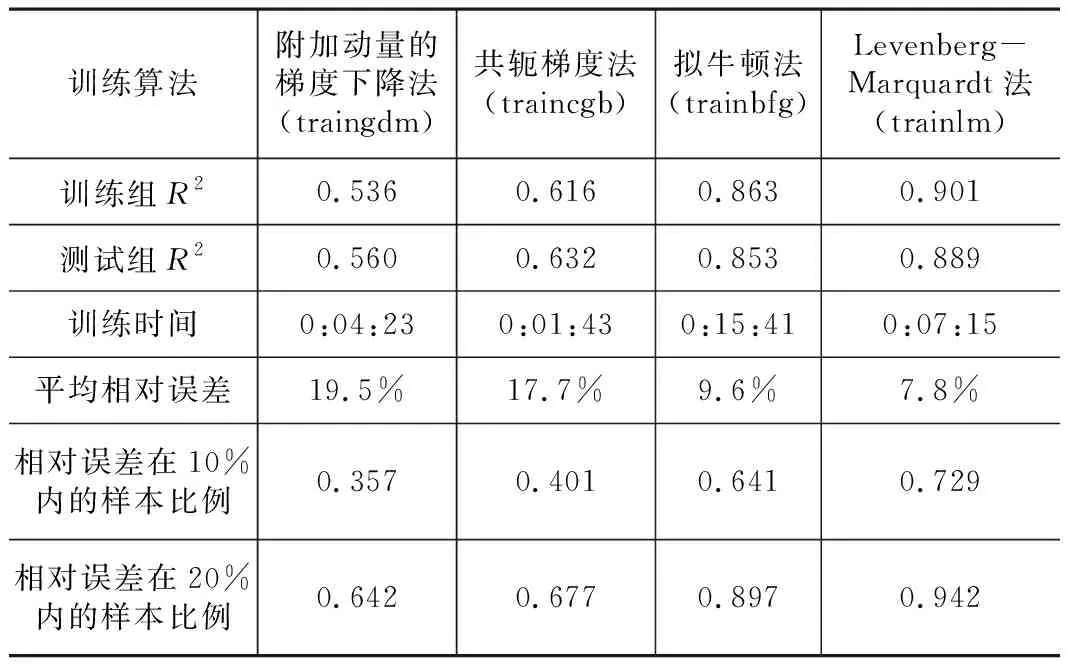
基準價網絡不同算法估價結果 表2
在基準價網絡上進一步輸入特定小區的二手住宅樣本進行小區估價模型訓練,這里以兩個小區(如表3所示)為例,給出估價結果的相對誤差(如表4所示)。小區武漢天地御江璟城在江岸區,所有樣本沒有參與基準價網絡訓練,小區世紀江尚在江漢區,均價低于武漢天地,部分樣本參與了基準價網絡訓練。
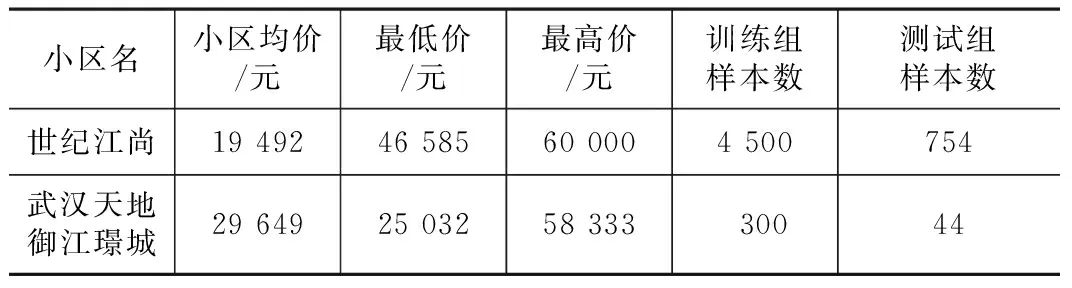
小區價格分布及樣本數量 表3
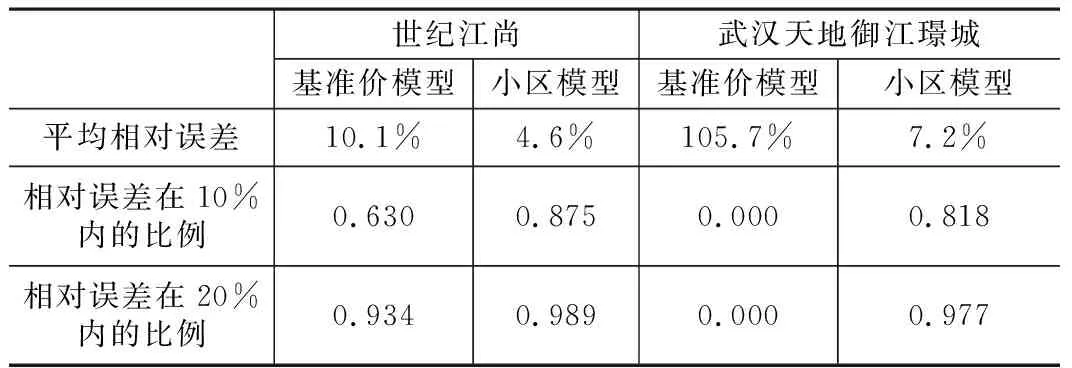
小區估價模型精度比較 表4
如表4所示,小區模型的估價精度均優于基準價模型,說明分級模型對精度有提高作用。在訓練世紀江尚的小區模型時,迭代10次便達到了表中的精度,證明在基準價網絡上訓練模型,能夠提高效率。世紀江尚的部分樣本參與了基準價模型訓練,用基準價模型直接估價時,平均相對誤差小;武漢天地的樣本沒有參與基準價網絡訓練,直接用基準價模型平均相對誤差達到了105.74%,說明將小區樣本納入基準價模型的必要性。整體上看,兩個小區模型估價結果的相對誤差在20%內的比例均達到了95%以上,具備實際應用能力。
4 總 結
本文應用特征價格理論確定14個房價影響因子,與神經網絡結合,建立了武漢市二手住宅估價的兩層分級模型。一方面,在基準價網絡基礎上訓練針對特定小區的網絡,訓練時間縮短,提高了效率;另一方面,通過將所有小區的部分樣本納入整體的基準價模型,可以保證模型的泛化能力,再訓練特定的小區估價模型,能夠提高估價精度。此分級模型為自動批量評估系統的實現提供了一種可行思路。
對于面向海量數據的房價自動評估系統,要進一步提高估價精度,除探索效率更高的估價算法外,可從數據著手,提高輸入的數據質量,這一點或可通過引入有效的異常點自動挖掘算法實現。

