混合驅動水下滑翔器滑翔效率及優化研究

肖冬林，張 華，李迎華，趙橋生

（中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

水下滑翔器是一種通過剩余浮力做功提供前進動力，通過內部滑塊移動進行姿態調節從而實現垂直面內鋸齒形運動的新型無人水下航行器。它有著工作時間長、工作范圍廣、能耗低、噪音低等諸多優點，在海洋環境監測、水下探測、通信等領域有著重要的應用[1]。同時，常規浮力驅動水下滑翔器也有著航速低、機動性差的缺點，不利于障礙物規避及在狹窄、淺水及強海流水域航行。混合驅動水下滑翔器結合了AUV和水下滑翔器的優點：在動力推進模式下，有著較好的機動性；在滑翔模式下，有著較高的續航能力，能夠執行更為復雜的水下探測作業任務。

續航力是水下滑翔器的重要性能指標，為了提高水下滑翔器的航程，需要降低能耗，提高滑翔效率。滑翔器的滑翔效率與水動力外形、滑翔姿態、剩余浮力大小、搭載儀器功耗等諸多因素有關。文獻[2]研究了不同類型滑翔器運動狀態、剩余浮力大小等對滑翔器滑翔效率的影響。文獻[3]從做功的角度研究了滑翔姿態對滑翔器滑翔效率的影響；文獻[4]分析了機翼展弦比、后掠角對升阻比的影響；文獻[5]研究了螺旋槳對混合驅動水下滑翔器阻力及航程的影響。以上文獻在分析滑翔效率時均沒有綜合考慮水平速度，而水平速度是滑翔器的重要性能指標之一。

本文從平面定常運動基本方程出發，給出了單位重量滑翔器為獲得單位水平速度所需能耗的數學表達式，作為一種基于運輸經濟性的滑翔效率評價指標。本文分析了滑翔姿態對水下滑翔器滑翔效率的影響及螺旋槳轉動模式對混合驅動水下滑翔器滑翔效率的影響。分析所需的各種驅動情況下滑翔器的流體動力系數由CFD方法獲得。

1 水下滑翔器效率評價指標

1.1 受力分析

對滑翔器垂直面定常滑翔狀態進行受力分析，如圖1所示，其中D表示阻力，L表示升力，M表示滑翔器受到的俯仰力矩水動力，α表示攻角，ξ表示滑翔角（速度與水平方向的夾角），m0g表示剩余浮力，坐標原點O位于均衡態滑翔器的浮心。

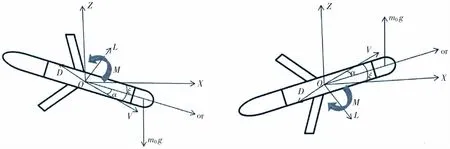
圖1 水下滑翔器受力分析（左：下潛，右：上浮）Fig.1 Analysis of the force of underwater glider(Left：down,Right：up)

受力平衡需滿足：

式中：l表示剩余浮力作用中心到坐標原點O的距離，ZG表示重心垂向坐標，m表示滑翔器質量。滑翔器水動力系數無論滑翔模式或動力推進模式均可以按下式進行簡化[7]：

1.2 滑翔效率指標

從能耗的角度研究滑翔器的續航力，本文采用的指標為單位重量水下滑翔器移動單位水平距離所需能耗：

式中：E表示能耗系數，W表示重量為mg的滑翔器水平移動距離為s時的總能耗，Vx表示平均水平速度，P表示平均功率，包括浮力調節系統平均功率P0（P0=m0gVz/η0=DV/η0，m0g表示平均剩余浮力大小，Vz表示平均垂直速度大小，η0表示剩余浮力調節系統機械效率），姿態調節系統、傳感器等搭載儀器及通信系統平均功率P1，對于混合驅動滑翔器，還包括推進系統功率P2（P2=2πnQ/η2，n、Q分別表示螺旋槳轉速、扭矩，η2表示螺旋槳電機效率）。顯然，能耗系數E越小，水下滑翔器滑翔效率越高。

對于螺旋槳不做功（或不帶槳）和螺旋槳做功的情況，將剩余浮力做功及螺旋槳做功展開，則（7）式可分別改寫為如下形式：

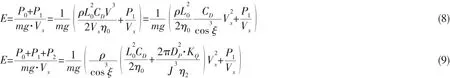
式中：DP表示螺旋槳直徑，KQ表示螺旋槳扭矩系數，J表示進速系數。

對于特定水下滑翔器，總長L0、η0、η2和P1均可認為是定值。當螺旋槳不做功時，（8）式中阻力系數CD及滑翔角ξ可認為僅與滑翔姿態（攻角α）有關；當螺旋槳做功時，（9）式中CD及ξ與攻角α及進速系數J有關，KQ、ω主要與進速系數J有關。因而當螺旋槳不做功時，能耗系數與水平滑翔速度Vx及滑翔姿態（攻角α）有關；當螺旋槳做功時，能耗系數還與螺旋槳進速系數有關。

（8）、（9）式均可改寫成如下形式：

式中：括號中第一項表示滑翔器克服水動力阻力的功耗，移動單位水平距離所需能耗與速度的平方成正比；第二項表示滑翔器搭載儀器設備功耗，移動單位水平距離所需能耗與水平速度成反比。按物理意義，顯然有 f（ α, J ）在定義域內有界，并恒大于零。故 f（ α, J）必存在極小值。而對任何 （α, J），因f（ α, J ）恒大于零，當 P1＞0，f1（α, J,Vx）必有極小值。

若 f（ α, J ）在定義域內存在最小值，對應的最優攻角、最優進速系數分別記為 αP、JP，再對（10）式求導，可得到使得E取得極小值最優水平速度Vxp為：

由于 f（ α, J ）主要與滑翔器水動力性能有關，本文主要研究使f（ α, J）取得極小值的最優滑翔姿態（最優攻角αP）及螺旋槳最優進速系數JP。

得到了最優滑翔姿態及最優水平速度，并獲取最優滑翔狀態下的水動力，根據受力平衡方程（1）～（3）可得到水下滑翔器的最優剩余浮力m0g及相應的剩余浮力力臂l。

當 P1=0 時，Vx在 f（ α, J ）最小時，可以在方程（1）～（3）范圍內任意選擇設計值，此時的能耗系數一定是對應該Vx最小。

2 浮力驅動水下滑翔器滑翔效率分析

浮力驅動水下滑翔器通過剩余浮力做功克服滑翔過程中的阻力，保持垂直面內鋸齒形的運動。滑翔器的運動狀態如速度V、攻角α、滑翔角β等對滑翔效率有著重要的影響，此節中將采用所建立的效率評價指標來分析這些變量對滑翔器滑翔效率的影響，并對滑翔器剩余浮力大小及剩余浮力力臂進行優化設計。

2.1 計算驗證

研究的水下滑翔器模型主體長度2.15 m、直徑0.3 m，水平翼展長1.2 m、后掠角30°。采用CFD方法計算滑翔器的水動力，網格劃分如圖2所示。風速V=16 m/s下，fluent軟件計算的垂向力系數與風洞試驗數據對比如圖3所示。

圖2 網格劃分（左：滑翔器表面網格，右：計算域網格）Fig.2 Meshing(Left：mesh of the glider surface,Right：mesh of computation domain)

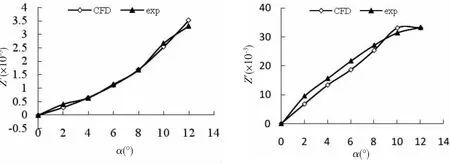
圖3 CFD計算結果與試驗結果比較（左：主艇體，右：帶附體）Fig.3 Comparison of CFD simulation and experiment result(Left：hull,Right ：glider with wings)

主艇體垂向力系數計算結果與風洞試驗結果攻角2°以上平均相對誤差為3.32%，最大誤差6.34%。帶翼滑翔器垂向力系數與風洞試驗結果攻角2°以上平均相對誤差為8.3%，最大誤差為14.8%。帶翼滑翔器計算誤差略大，主要是由于計算模型沒有考慮尾穩定翼、天線等附體。整體上計算誤差在可接受范圍內，故可用于本文效率評價。

2.2 變攻角、變速度滑翔效率分析

固定來流速度V，改變攻角α，數值模擬獲得滑翔器在不同工況下的水動力系數、升阻比λ如圖4所示。

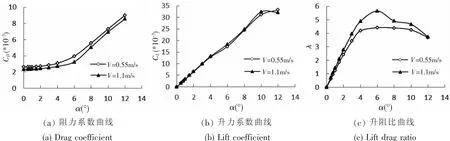
圖4 水動力隨攻角變化曲線Fig.4 Hydrodynamic-attack angle curves

由圖4可知，水下滑翔器的阻力系數CD、升力系數CL及升阻比λ（或滑翔角）主要與攻角α有關，隨速度變化不大；在小攻角范圍內，CD、CL基本上隨α單調遞增，本滑翔器在攻角約為6°時，升阻比達到最大值。

再根據（4）～（6）式，采用最小二乘法回歸得到各水動力系數如表1所示。

表1 水動力系數計算結果Tab.1 Hydrodynamic force coefficient of underwater glider

由于計算對象上下完全對稱，故KL0、KM0大小為0。假定水下滑翔器剩余浮力調節系統機械效率η0=40%，結合（1）～（6）式，可得到圖 5 所示的 f（α）-α 曲線。

根據計算的結果，得到f（α）取得最小值的攻角αP≈2.8°。

假定水下滑翔器搭載儀器功率P1=3 W，由（7）式可得到最優水平速度Vxp≈0.42 m/s。

通過受力平衡方程（1）～（3），可得到最優滑翔狀態下的剩余浮力m0g≈4 N，剩余浮力力臂l≈0.588 m。

作為比較，給出相同剩余浮力（m0g≈4 N）下升阻比λ最大時的滑翔姿態、滑翔速度及能耗系數，如表2所示。

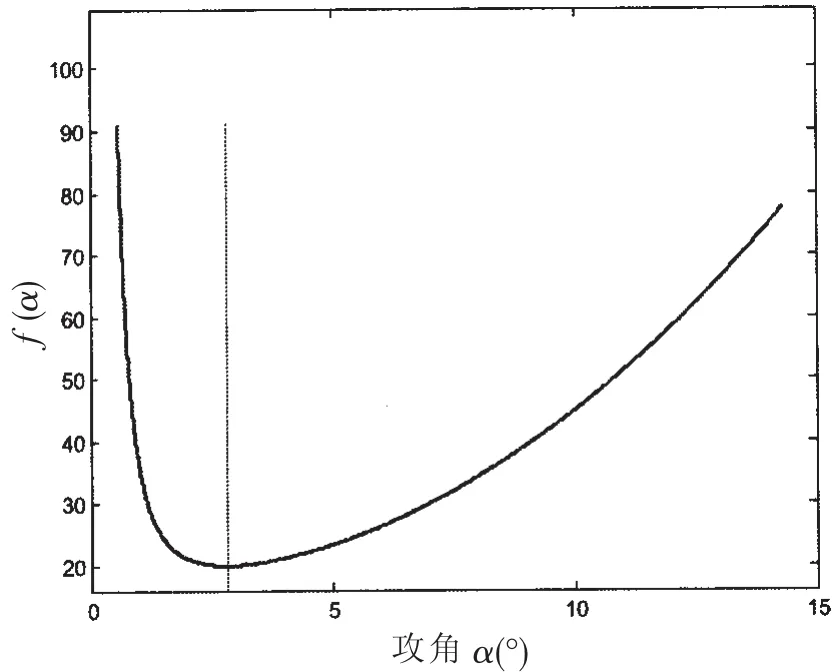
圖 5 f（α）-α 曲線Fig.5 f（α）-α attack angle curves

表2 不同滑翔姿態下的滑翔效率比較Tab.2 Comparison of gliding efficiency in different gliding mode

計算結果表明最大升阻比并不代表滑翔效率最高，相同剩余浮力條件下，滑翔器以本文得到的最優滑翔姿態滑翔較最大升阻比姿態能耗系數可降低20%，且水平滑翔速度較高。

3 混合驅動水下滑翔器效率分析

混合驅動水下滑翔器有滑翔模式及動力推進模式兩種工作模式。在滑翔模式下，滑翔器主要通過剩余浮力做功提供前進動力，進行垂直面鋸齒形運動；而在動力推進模式下，推進系統提供動力，完成水平運動或其它機動。混合驅動滑翔器大多數時間工作在滑翔模式下，螺旋槳的存在會增大阻力、增大滑翔器功耗，降低航程。

在滑翔模式下，混合驅動滑翔器的螺旋槳可以固定不動，也可以在水流的作用下隨動轉，還可以做功主動低速轉。對于斜流下螺旋槳非定常水動力的計算，fluent提供了滑移網格技術和動網格技術，其中滑移網格技術比較簡便實用。本文采用滑移網格技術計算艇后螺旋槳的水動力。應用所建立的滑翔效率指標，評價了螺旋槳對滑翔器滑翔效率的影響及螺旋槳轉動方式對滑翔效率的影響。

3.1 計算驗證

計算對象為前述帶翼滑翔器及尾部直徑0.125 m的三葉槳構成，網格劃分如圖6所示。計算域分為包含螺旋槳的旋轉區域及靜止區域兩部分，其中，靜止區域采用全結構化網格，而旋轉區域采用非結構化網格，網格總數為200萬。

圖6 混合驅動滑翔器網格劃分（左：艇體表面網格，右：尾部附近網格）Fig.6 Mesh of HUG(Left：mesh of the surface,Right：mesh near the propeller)

由于目前缺乏帶槳滑翔器的試驗數據，本文僅對螺旋槳敞水計算進行驗證。選用的螺旋槳型號為P4119三葉槳，盤面比為0.6，直徑0.25 m。計算域為全流域，計算模型選擇滑移網格模型。CFD計算結果與圖譜的比較如圖7所示。

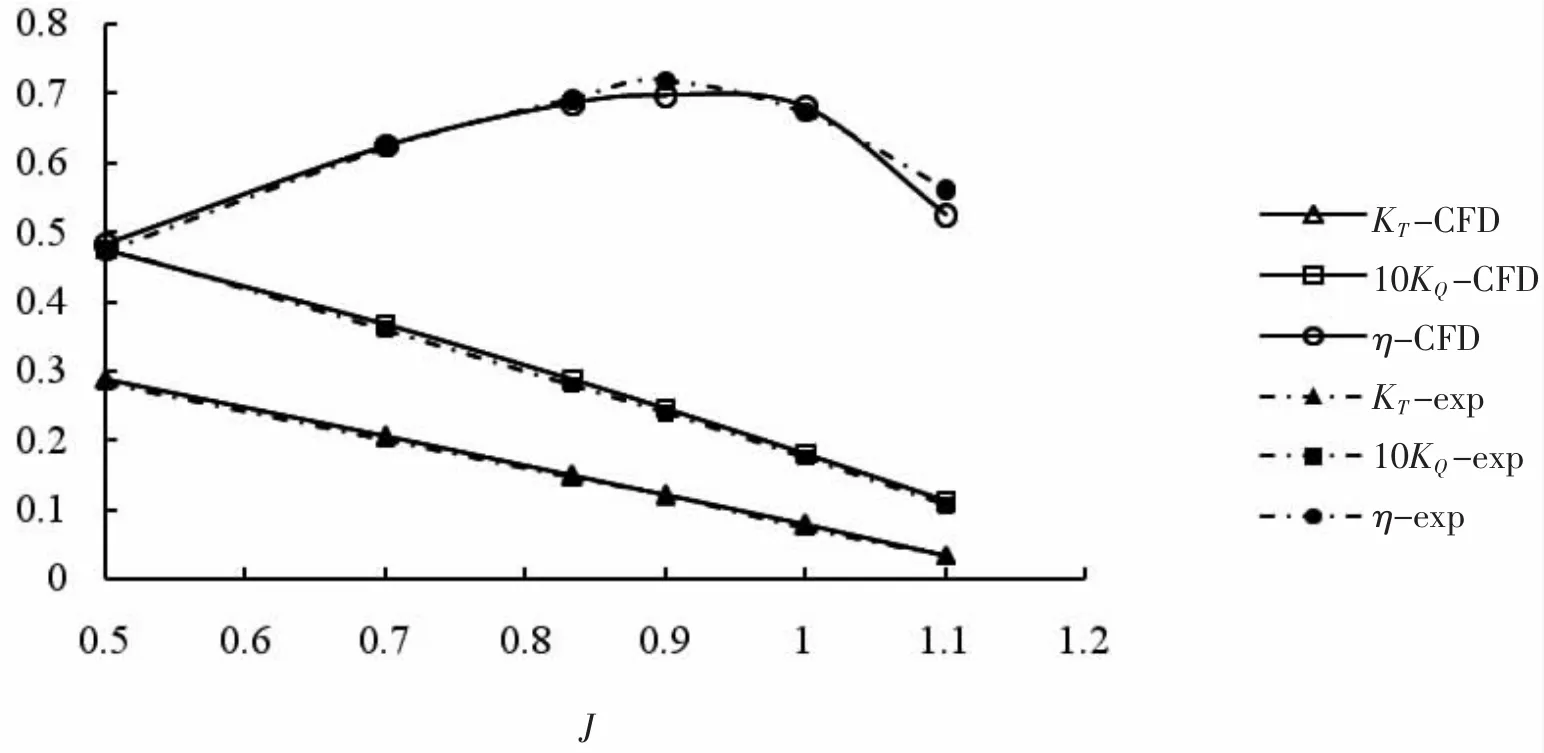
圖7 敞水槳CFD計算與試驗結果比較Fig.7 Comparison of open-water characteristics of propeller by CFD and experiment

由上圖可知，推力系數KT計算值與試驗值平均誤差為1.96%，最大誤差為4.80%；扭矩系數KQ計算值與試驗值平均誤差2.84%，最大誤差5.78%；敞水效率η計算值與試驗值平均誤差2.32%，最大誤差6.68%。計算結果表明，所采用的數值方法是可行的。

數值計算中，固定來流速度和攻角，改變螺旋槳的轉速。不同轉速下，螺旋槳提供的推力不同，導致滑翔器的總阻力和總升力也不同。根據力的平衡關系（1）-（3），可以得到每個轉速下的滑翔角或者升阻比及平衡所需的剩余浮力大小。

3.2 螺旋槳不做功時的滑翔效率分析

當螺旋槳不轉或在水流的作用下隨動轉動時，螺旋槳不輸出功率。不考慮螺旋槳電機阻尼，隨動轉時螺旋槳阻尼為零。不同攻角下，不帶槳、帶槳槳不轉及隨動轉CD、λ及f（ α, ）J比較如表3所示。

由計算的結果可知不同攻角下螺旋槳不轉時較不帶槳滑翔器阻力約增大了14%，升阻比約降低了 10%， f（ α, ）J增大18%～21%；螺旋槳在水流的作用下隨動轉，較槳不轉滑翔器阻力減小8%～9%，f （ α, ）

J減小10%～16%。這說明在滑翔狀態下（僅剩余浮力做功），混合驅動滑翔器讓槳隨水轉動比槳鎖住要好得多。

表3 隨動轉、槳不轉及不帶槳變攻角計算結果比較Tab.3 Gliding efficiency analysis comparison between propeller driven by water,propeller fixed and without propeller

3.3 主動低速轉動時的滑翔效率分析

固定來流速度及攻角大小，逐漸增大螺旋槳轉速，得到不同轉速下滑翔器的總阻力、總升力及螺旋槳的扭矩。據此可以得到滑翔器在不同進速下的升阻比λ及及f（ α, ）J曲線。計算結果如圖8所示。

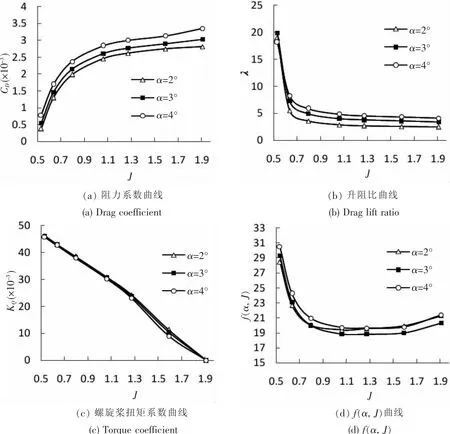
圖8 變進速系數下的滑翔效率分析Fig.8 Gliding efficiency analysis of HUG with different advance coefficient

計算結果表明：對于攻角α=2°、3°和4°三種工況，雖然槳的伴流分數會略有不同，但其槳的扭矩特性基本不變（圖8（c））；無論是阻力系數，還是升阻比，在所有J的計算范圍內，攻角α=3°處于居中地位（圖 8（a），8（b））；當 J＞0.8 開始，α=3°工況的 f（ α, ）J在三者之間始終處于最低位，并在J≈1.27左右達到最小值，這也是三種工況下的最小值。

同時，J≈1.27 處的 f（ α, ）J也明顯比螺旋槳隨動轉工況（螺旋槳扭矩系數為0，J≈1.9）小。因而驅動電機工作，槳在J=1.27，攻角3°時，滑翔效率最佳，且優于定槳或隨動槳。

4 結 論

本文從平面定常動力學方程出發，提出了水下滑翔器效率的評價指標，即單位滑翔器重量、單位水平速度所需能耗。

（1）基于此指標，給出了能耗系數的數學表達式，求其最小化的最優途徑。為工程產品的設計，提出了有效工具。最優解對工程設計有較大參考價值。

（2）對于特定的浮力式水下滑翔器，按文中方法，得到其滑翔效率最高的攻角為2.8°，水平速度為0.42 m/s，剩余浮力 4 N。

（3）對于具體的混合驅動水下滑翔器，本文方法得到：若驅動電機不工作，讓槳隨水轉動比鎖住滑翔效率高，而槳的存在總是增加能耗，降低效率；若驅動電機工作，則槳在J=1.27，攻角3°時，滑翔效率最佳，且優于定槳或隨動槳。