單相電源法測量單回不對稱線路阻抗參數的誤差分析與改善措施

董清，邵鵬程

(華北電力大學 電氣與電子工程學院，河北 保定 071003)

0 引 言

隨著電力系統規模的擴大，電網的結構日益復雜，線路走廊日趨緊張，為了節省線路走廊占地面積，減少線路建設成本，大多數的輸電線路采用了不換位的架設方式，因此三相線路的參數會產生一定的不對稱[1]，準確測量出每相線路的參數成為了研究的熱點，線路參數對潮流計算、短路計算和繼電保護整定有很大的影響，直接影響計算的準確性[2-5]，線路參數的準確測量與計算對電力系統的穩定運行具有積極的意義，新建高壓輸電線路在投運前[6-8]，除檢查線路絕緣、核對相序、測量直流電阻外，還需要測量各種工頻參數[9-14]，其中線路的三相阻抗參數[15]就是之一，目前現有的線路參數測量方法[16]，如異頻法、工頻法、掃頻法和帶電測量法，這些方法都是假定線路參數對稱的情況下使用的，而對于單回不對稱線路參數的測量方法很少，基于三相阻抗參數不對稱的基本原理，目前提出了單相電源多變換接入方式的不對稱輸電線路參數分相解耦測量方法，這種方法的實質是一種單端測量[17]的方法，但是此種方法由于電流矩陣的求逆運算，在計算單回不換位線路三相阻抗參數時存在一定的誤差，該文對此誤差進行了定量的分析，并且提出了采用雙端測量的方法在計算單回不換位線路三相阻抗參數時可以減小誤差，由于測量電路當中考慮了大地電阻[18]對單回不換位線路三相阻抗參數計算的影響，該文提出了一種新的測量大地電阻的方法，這樣能夠更加準確的計算單回不換位線路三相阻抗的參數，最后以一條500 kV單回不換位線路驗證了雙端測量方法減小誤差的可行性。

1 常規測量線路阻抗參數方法的誤差分析

單回不換位線路三相阻抗參數分相解耦測量方法是通過在單相與地之間施加單相工頻測試電源，線路末端三相短路然后與大地構成回路，在線路首端A相與地之間施加單相工頻測試電源，同理，還可在B相與地之間、C相與地之間施加單相工頻測試電源，根據測量得到的數據建立數學模型，得到一系列約束方程，將方程求解得到線路參數，測量電路圖如圖1所示。

圖1 單回不對稱線路參數測量電路

RA=RB=RC，XA≠XB≠XC

根據電路原理和測量數據，可以得到如下方程：

(1)

(2)

(3)

(4)

聯立式(1)～式(3)，將測量結果寫成矩陣形式，表達式如下：

(5)

其中：

(6)

(7)

(8)

(9)

(10)

其中單位矩陣E表示如下：

(11)

(12)

由式(12)可知，根據測量得到的電壓、電流量可以求出各相阻抗參數和大地電阻的大小。當線路參數有很小的不對稱性時，由于電流矩陣的求逆運算，最后會導致計算出的各相阻抗參數和大地電阻產生很大的誤差，具體誤差推導如下：

(13)

(14)

(15)

2 雙端同步測量線路阻抗參數的方法

由于大地電阻的測量受到土壤電阻率、干擾信號等因素的影響，在測量當中會出現誤差，因此本文提出了采用雙端測量求大地電阻的方法，雙端測量方法采用全球衛星定位系統可以測出線路首、末端電壓和電流，測量的電路如圖2所示。

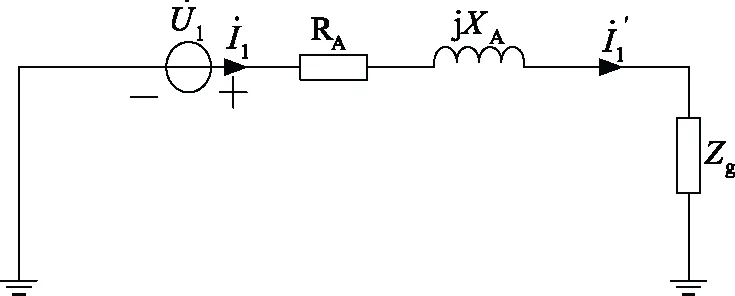
圖2 大地電阻測量電路

圖2的大地電阻測量電路當中，以A相線路為例，在線路首端施加單相工頻測試電源，利用雙端測量的方法可以測出首端的電壓、電流和末端的電流，由KVL可得：

(16)

聯立式(1)與式(16)可以求解得到大地電阻：

(17)

下面介紹利用雙端測量求不對稱三相阻抗參數的方法，由圖1可知，對節點N列節點電壓方程：

從而可得節點N的電壓表達式：

(18)

利用雙端測量方法可以測得大地電阻的大小，在圖1當中三相不對稱線路首端分別施加了單相工頻電源，線路首端的電壓、電流都可以測量得到，節點N的電壓又可以表示如下:

(19)

(20)

(21)

(22)

3 單回不對稱三相阻抗參數單端測量的誤差分析

針對單回不對稱三相阻抗參數的測量問題，在前文介紹了分相解耦測量方法，實際上是一種單端測量的方法，此方法是通過在單相與地之間施加單相工頻測試電源，根據各相分別施加單相工頻測試電源測到的線路首端電壓、電流數據建立數學模型，得到一系列約束方程，將方程求解得到不對稱三相阻抗參數和大地電阻的值，當單回輸電線路的三相阻抗參數不對稱時，電流矩陣的求逆運算會對參數的求解造成一定的誤差，聯立式(12)、式(20)～式(22)求得各相阻抗參數的誤差大小分別如下：

(23)

(24)

(25)

相對于雙端測量方法計算單回不對稱三相阻抗參數而言，ΔZA、ΔZB、ΔZC分別為采用分相解耦測量方法計算A、B、C三相阻抗所產生的誤差，在實際測量中，為了減小測量誤差，采用雙端測量方法計算單回不對稱三相阻抗參數更加準確。

4 單回不對稱線路算例分析

由于高壓線路不換位的現象日益增多，因此選取電壓等級為500 kV的單回不對稱線路進行計算分析，根據《電力系統設計手冊》可知，選擇500 kV架空輸電線路的型號為4×LGJ-400/50，導線參數詳見表1。

表1 4×LGJ-400/50導線參數

測量用的單回不對稱輸電線路的長度l=100 km，輸電線路的各個參數的計算過程如下：

R=rl=0.018 08×100=1.808 Ω,X=Ll=

0.277 47×100=27.747 Ω

由于各相線路阻抗參數的關系如下：

RA=RB=RC，XA≠XB≠XC。

因此可令單回不對稱線路各相阻抗參數如下：

RA=RB=RC=1.808 Ω，XA=27.747 Ω，

XB=30.5217 Ω，XC=33.296 4 Ω。

根據卡爾遜的推導[19]，大地電阻的公式可以表示為Zg=9.869×10-4f(Ω/km)，在工頻50 Hz的情況下，Zg=0.05 Ω/km，因此當單回不對稱輸電線路的長度為100 km時，利用雙端測量求大地電阻的方法可以令大地電阻的值Zg=5 Ω，A、B、C三相與地之間施加的單相工頻電壓大小分別如下：

又由式(5)，聯合式(10)，從而求得阻抗矩陣：

根據前面推導出的不對稱三相阻抗的誤差公式(23)～式(25)可得各相阻抗的誤差：

ΔZA=(0.690 5+j0.133 5) Ω

ΔZB=(-0.534 5+j0.576 9) Ω

ΔZC=(-0.237-j0.779 1) Ω

根據分相解耦測量方法求得的大地電阻Zg=(-0.458 2-j1.001 5) Ω，對于100 km輸電線路利用雙端測量求大地電阻的方法把大地電阻的值取為5 Ω，由此可以看出采用分相解耦方法求單回不對稱線路三相阻抗參數和大地電阻參數會產生很大的誤差，從而對輸電線路的運行計算產生很大的影響，因此采用雙端測量的方法求大地電阻和三相阻抗參數更為準確，有利于輸電線路的設計。

5 結束語

本文針對高壓單回不對稱線路阻抗參數的分相解耦測量方法進行了分析，并且針對此種方法計算阻抗參數和大地電阻產生誤差的原因進行了分析，由于電流矩陣的求逆運算，在使用分相解耦方法求解阻抗參數和大地電阻時會產生很大的誤差，經過分析得到了各相阻抗由于電流矩陣求逆產生誤差的大小，為了減小誤差，該文提出了雙端測量的方法求解阻抗參數和大地電阻，最后以一條500 kV單回不對稱線路為例，驗證了使用雙端測量的方法更能準確的測出實際的阻抗參數和大地電阻的大小，準確的測量線路參數對潮流計算和電力系統的安全穩定運行具有重要的意義。