基于價格預測的水運工程材料價格決策研究

姚卓宏

湖南省交通規劃勘察設計院有限公司，湖南長沙 410005

1 水運工程投標報價現狀

在水運工程投標過程中，一般是采用現在的市場材料價格進行綜合單價組價，再加上一個市場材料價格上漲的風險費用。目前風險費用一般是通過主觀預測確定的，需要一種科學的方法來避免材料價格上漲帶來的不利影響。

2 水運工程材料的動態價格決策模型

對材料價格變化應采用客觀科學方法對其做出更加準確的預測，同時還應將預測得到的材料價格和施工組織設計中的材料需求供應計劃結合，通過分階段計算出符合施工進度計劃的材料平均價格，即采用動態價格決策模型來對水運工程建設材料價格作出更加準確的估計，如圖1所示。

2.1 市場價格的變權重組合預測模型

水運工程材料價格是一個較復雜的變量，影響因素多，若將灰色系統與神經網絡結合起來，構成組合預測模型，能夠充分發揮各單項預測方法的優勢。

為了能夠更好地適應預測環境的變化，選取變權重組合預測模型來進行預測。設對于同一個預測問題，有n種預測方法f1，f2，…，fn，則由這n種預測方法組成的組合預測模型為：

式中：y（t）—變權重組合模型在t時刻的預測值；gi（t）—第i種模型在t時刻的權重系數 ；fi（t）—第i種模型在t時刻的預測值。

設eit、et分別為第i種模型和變權重組合模型在t時刻的預測誤差，則相應的表達式為：

式中：Y（t）—在t時刻的實際觀察值。

確定組合預測變權重系數的方法是使樣本點處組合預測的誤差最小，同時還要滿足權重系數自身的要求，因此可得到如下組合模型的優化模型[1]：

（1）對于在t時刻的樣本點，各種單一的預測模型均有eit≥0（或者eit≤0）的情況。假設此時第p種預測模型的誤差最小，∣ept∣=min∣eit∣，則模型的解：

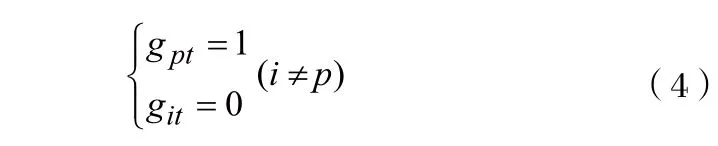
（2）對于在t時刻的樣本點，各種單一預測模型的誤差中有一部分eit≥0，另一部分eit＜0的情況。假設此時所有預測誤差為非負數的模型中第P1種模型預測誤差的絕對值最小；所有預測誤差為負數的模型中第P2種模型預測誤差的絕對值最小。此種情況下模型的解為[2]：

在進行預測時，預測時刻t（t=r+1，r+2，…，r+z）處的各個預測模型的權重系數，可以按照下式計算求得。

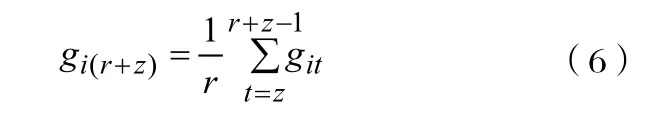
式中：r—預測時所選基礎樣本點的個數。

2.2 材料需求供應計劃

在編制水運工程施工組織設計時，根據材料需求量和施工進度計劃編制材料供應計劃。

2.3 材料平均價格的確定

根據動態價格決策模型，如水運工程從開工之日起到工程竣工之日止，工期為n期，則該水運工程第k（k=1，2，3，…）種材料平價格確定的具體步驟如下：

（1）根據施工組織設計中資源需求計劃，可得到每期第k種材料的需要量為vi，則V=（v1，v2，…，vn）；

（2）根據市場價格預測，可得到每期第k種材料的預測價格為pi，其中i=（1,2，…，n）則P=（p1，p2，…，pn）T；

（3）該水運工程預測的第k種材料總的費用為：C=V×P，第k種材料的平均價格為：

3 實例應用分析

以湖南某碼頭工程為例，該工程建設工期為1年，開工日期為2010年10月。

3.1 水運工程材料價格相關數據

考慮到水運工程建設對鋼筋需求量大，下面以螺紋鋼為例進行分析。通過對該碼頭工程編制施工組織設計，可得到該碼頭工程對螺紋鋼的需求供應計劃，如下：2010第4季度490t、2011第1季度390t、2011第2季度115t、2011第3季度89t。

從2003第1季度到2011第3季度（共35期）的螺紋鋼價格數據如下（單位：元/t）：第1期到第10期：2872、3396、3396、3899、4431、3764、3935、3947、3961、3613；第11期到第20期：3293、3154、3210、3360、3286、3393、3716、3761、4154、4863 ；第21期到第30期 ：5252、5795、5565、4273、4129、3882、4326、4099、4201、4552 ；第31期到第35期 ：4430、4766、5090、5405、5298。

3.2 水運工程材料價格預測分析

3.2.1 預測模型預測

分別利用GM（1,1）模型、BP神經網絡模型和變權重組合模型進行預測，結果見表1。

表1 2010年第4季度到2011年第3季度的價格預測值（元/t）

3.3 水運工程材料平均價格的確定

由表1可知該碼頭工程對螺紋鋼HRB 335（Φ10以外）各季度的需求供應計劃為V=（490，390，115，89），由表4可知螺紋鋼HRB 335（Φ10以外）各季度的預測價格為P=（4699.69，5142.57，5375.17，5240.07）T，將P、V結合代入動態價格決策模型，得到C=V×P=5392962.18，進而求出螺紋鋼HRB 335（Φ10以外）的平均價格為

4 結語

本文綜合考慮了材料未來價格變化和需求供應計劃對整個水運工程建設過程中材料費用的影響，在此基礎上提出了動態價格決策模型，并通過實例證明了該模型在一定程度上提高了編制投標價時所用材料價格的準確度。