高靈敏高動態超緊組合跟蹤方法探討

吳飛燕，叢 麗，萬國龍

(北京航空航天大學 電子信息工程學院，北京 100191)

0 引言

全球衛星導航系統(global navigation satellite system，GNSS)接收機通過捕獲和跟蹤衛星信號實現定位功能[1]。影響捕獲和跟蹤性能的最主要因素是信號強度和載體動態[2]。衛星信號在室內、城市道路、叢林、峽谷等復雜環境下，會有不同程度的衰減[3]。針對弱信號的跟蹤，科斯塔斯(Costas)環路常用的改進方法為加長相干積分時間并運用窄帶濾波器[4]；其他環路有矢量跟蹤、基于離散傅氏變換快速算法(fast Fourier transformation，FFT)的頻域跟蹤等方法。其中本文采用加長相干積分時間的方法提高信噪比；采用FFT鑒頻代替普通鑒頻器，通過判斷信號在頻域中的峰值而準確估計多普勒頻率[5]。但是這將導致環路更新慢，對動態容忍性變差。高動態產生的多普勒頻移使得高靈敏環路相干積分增益產生損耗，并且FFT產生頻譜擴散，影響環路的穩定跟蹤。針對高動態，常采用超緊組合算法，用慣性導航系統(inertial navigation system，INS)信息計算的多普勒變化量輔助載波環，去除載體大部分動態[6]。該方法恰好可以彌補高靈敏環路無法忍受高動態的缺點。

鑒于以上分析，本文針對高動態、弱信號場景，提出了高靈敏高動態超緊組合跟蹤方法。

1 高靈敏高動態超緊組合載波跟蹤環算法模型

如圖1所示，上半部分框圖是高靈敏載波跟蹤環，通過加長相干積分時間提高信噪比、FFT鑒頻檢測弱信號頻率；下半部分是超緊組合環路，利用INS和衛星星歷信息對環路進行輔助，減弱環路跟蹤動態，并且組合結果對INS進行實時校正。

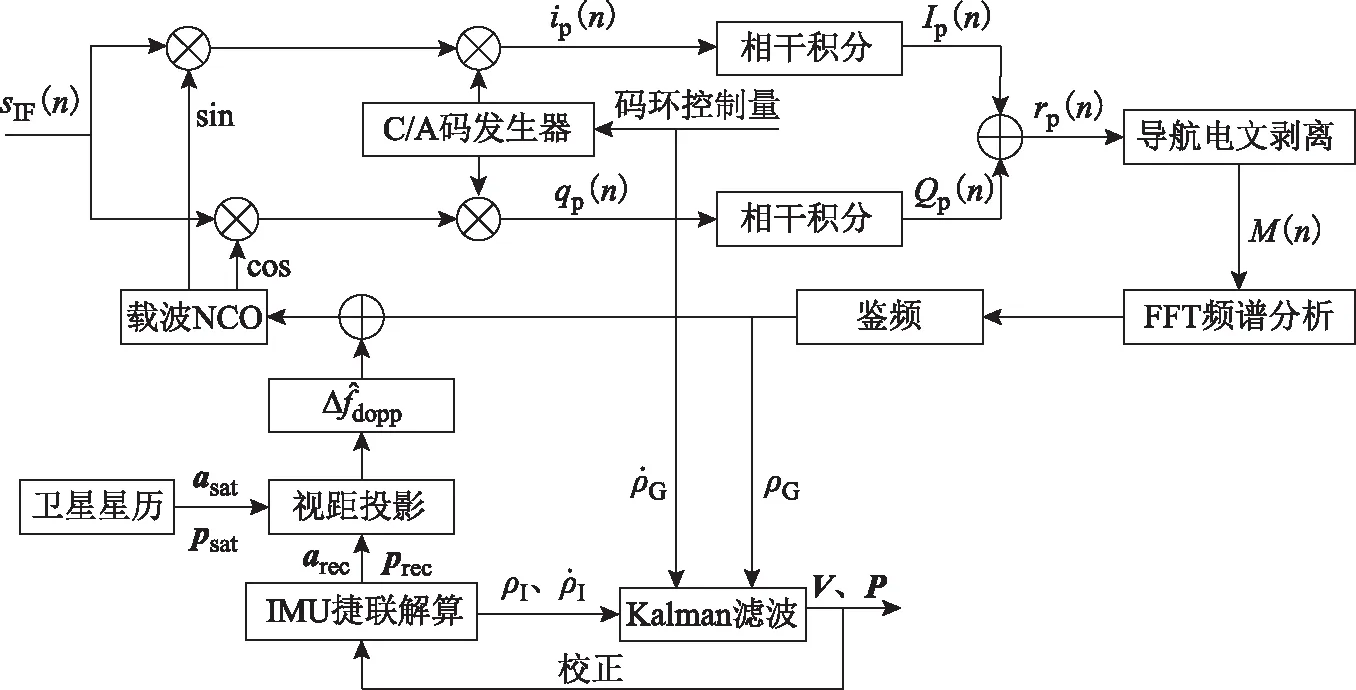
圖1 高靈敏高動態GNSS/INS超緊組合載波跟蹤環

首先，利用INS及衛星星歷信息估計載波環更新周期內的多普勒變化量，疊加在載波數控振蕩器(numerically controlled oscillator，NCO)的控制量上；接著進行混頻，混頻結果的低頻成分為輔助多普勒誤差，如果輔助信息較為準確，則該多普勒輔助誤差接近于0，載波環相當于跟蹤靜止或者低動態信號；然后碼環進行C/A碼相關運算，假設自相關結果為1，則相關后的信號為有著低頻率多普勒誤差的導航電文；接下來對該信號進行長度為Ncoh的相干積分運算，可以提高信噪比10lgNcoh(dB)；為了使FFT運算時信號不會正負抵消，需要進行導航電文剝離[7]；之后需要等待N個去除了導航電文的相干積分結果，進行N點FFT運算。對FFT的結果求幅值，幅度最大點對應的頻率值為多普勒頻率誤差的估計值[8]，該值與環路更新周期內INS輔助的多普勒變化量疊加，作為載波NCO的控制量；GNSS解算星歷得到的偽距、偽距率與INS推算的偽距、偽距率分別做差，差值作為卡爾曼濾波器的量測信息；INS與接收機的位置、速度及姿態誤差作為觀測信息，也即卡爾曼濾波結果，該結果對INS進行修正，形成整個閉合環路。

2 高靈敏環路載噪比分析

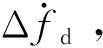
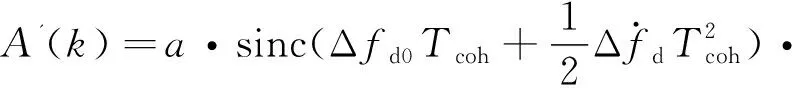
(1)

式(1)中多普勒變化率誤差將造成FFT運算結果幅值衰減，由于噪聲不受多普勒變化率的影響，所以其將導致的信噪比損失為

(2)

假設相干積分時間Tcoh=10 ms，多普勒初始誤差為Δfd0=0 Hz，則不同FFT點數與不同的多普勒變化率誤差對應的信噪比損失如表1所示。

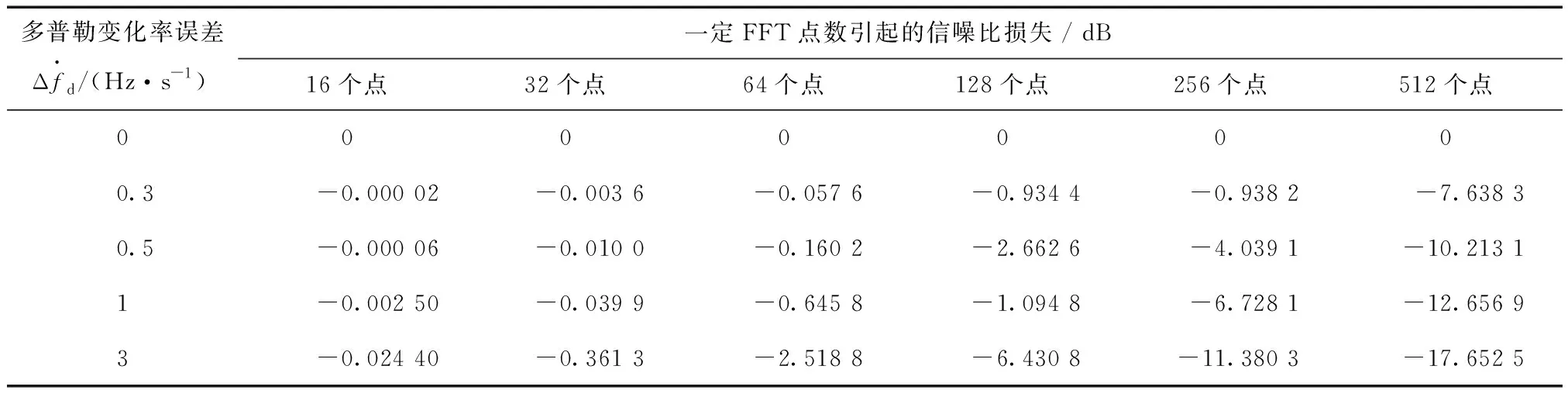
表1 不同FFT點數下不同多普勒變化率誤差引起的信噪比損失

設：接收GPS信號強度為PR=-177 dB·W；噪聲頻譜功率密度為N0，N0=kT，其中k為玻爾茲曼常數，其值為1.38×10-23J·K-1，T為開爾文溫度，設為290 K；預檢噪聲帶寬Bpd=2.046 MHz。進行C/A碼相關及長度為Tcoh的相干積分，加上基帶數字信號處理損耗2 dB，FFT運算后信號信噪比(如表2所示)為[9]：

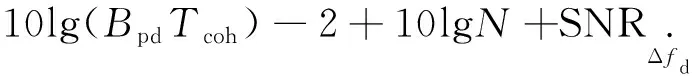
(3)

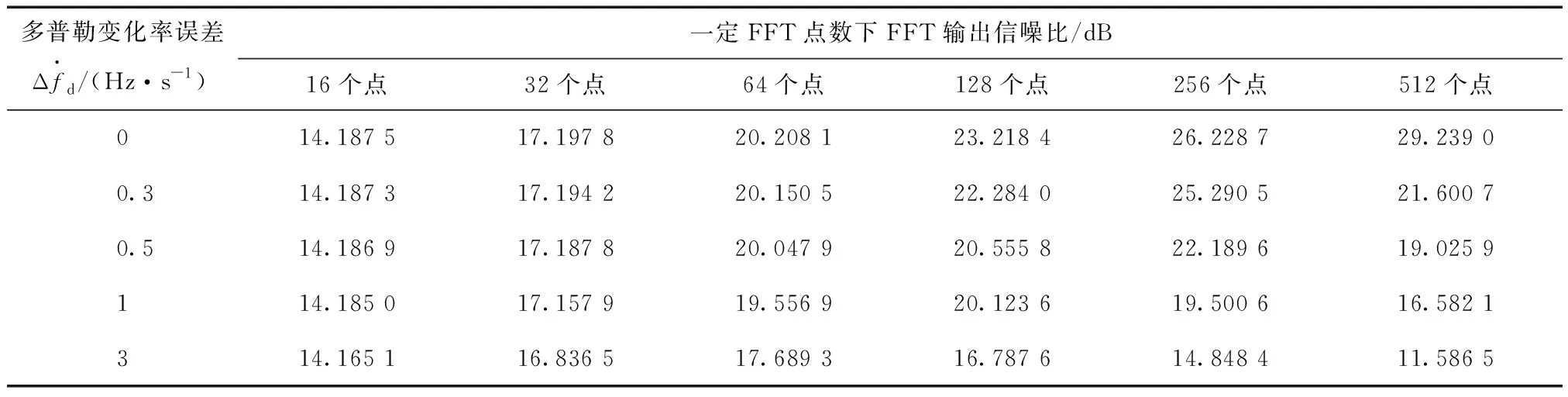
表2 不同FFT點數、不同多普勒變化率誤差下FFT輸出信噪比

3 INS輔助高靈敏載波跟蹤環

載波環失鎖，大部分是由載體動態較大導致的。多普勒變化率較大時，載波環本地復制信號與接收信號存在較大多普勒變化量誤差。高靈敏環路更新慢，這一缺點將導致多普勒變化量誤差加大，環路更容易失鎖。故采用加速度輔助載波環的方法，利用INS與衛星二者的加速度等信息計算出多普勒變化率，再乘以INS輔助間隔，作為INS輔助間隔內估計的多普勒變化量疊加在NCO控制量上。多普勒變化率是由載體動態以及晶振誤差、噪聲等引起的，其中載體動態是主要因素。忽略晶振誤差及噪聲后，輔助間隔內多普勒變化量可表示為

(4)

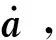
(5)

由式(5)可知，輔助間隔越小輔助誤差越小。圖2所示為輔助時間間隔與最大多普勒變化率的誤差關系。

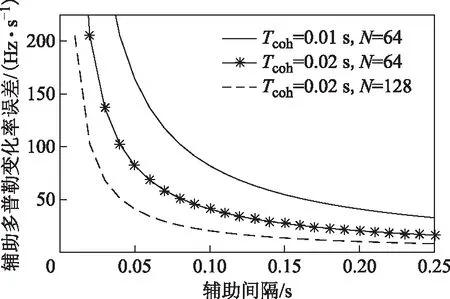
圖2 輔助時間間隔與最大多普勒變化率誤差關系

由圖可知，假設加速度無輔助誤差，輔助間隔越小，環路對加加速度容忍性越好；故輔助間隔越小越好。本文中載體位置及其加速度更新時間是INS更新時間，為2 ms；衛星加速度及其位置更新時間是環路更新時間，為640 ms。現將衛星加速度及其位置進行更新間隔內線性插值，使其更新時間也為2 ms，盡量減小輔助誤差，以保證環路更新時間內多普勒誤差不超過FFT鑒別門限。

4 實驗與結果分析

為了驗證高靈敏高動態環路的跟蹤性能，用模擬器模擬載體高動態軌跡，生成中頻數據、INS數據和運動軌跡。分別對高靈敏高動態環路和高靈敏環路進行測試，并將二者對高動態、弱信號的跟蹤性能進行對比。

4.1 仿真條件說明

首先設置高靈敏高動態環路和高靈敏環路的相干積分時間均為10 ms，FFT點數均為64個，環路更新時間均為640 ms，高靈敏高動態環路的INS輔助間隔為2 ms。

載體動態設置為：仿真時間150 s，載體軌跡為直線運動，初始位置為東經5°、北緯5°、高5 m，航向為90°，橫滾角、俯仰角均為0°。在0～50 s內載體靜止；50～150 s內加加速度為0.5 m·s-3，加速度斜升增加到500 m·s-2，速度增加到25 020 m·s-1(如圖3(a)、圖3(b)所示)。慣導的加速度計和陀螺儀的參數如表3所示。

表3 INS參數

用載噪比每秒下降0.5 dB·Hz的靜止模擬數據來測試高靈敏環路能跟蹤的最弱信號。在95.5 s時跟蹤丟失，此時估計的最低載噪比為20.74 dB·Hz，如圖4所示。考慮到一定的動態余量，設定2組高動態信號的最低載噪比分別為25、30 dB·Hz，具體設置為：0～40 s，保持42 dB·Hz；40～50 s內載噪比線性下降；50～150 s內，保持25、30 dB·Hz(如圖3(c)所示)。

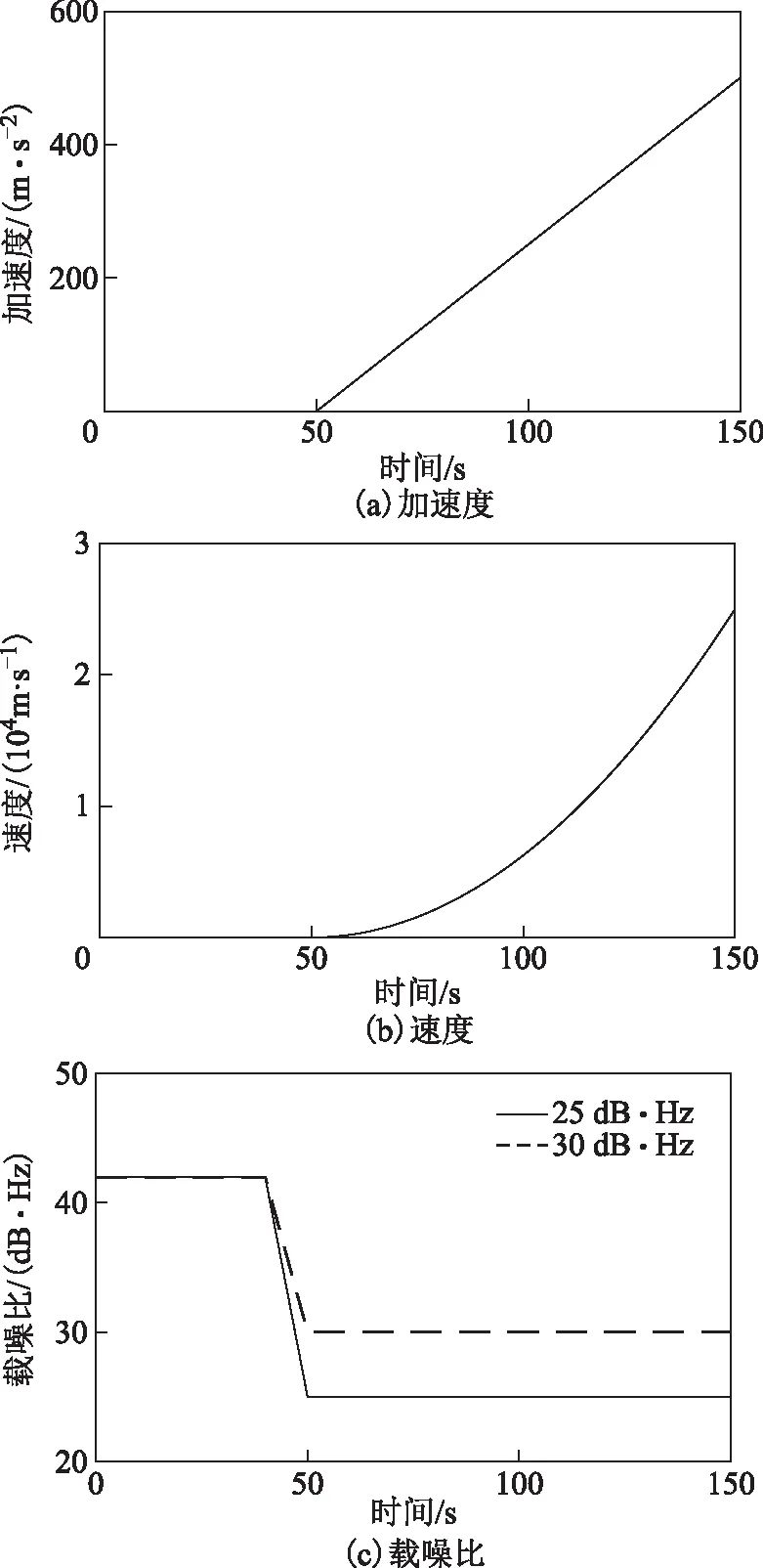
圖3 加速度、速度及載噪比模型

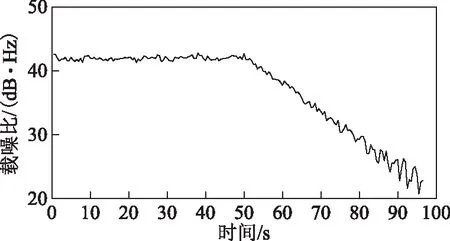
圖4 靜止狀態高靈敏環路跟蹤載噪比

4.2 仿真結果分析

1)跟蹤動態性能分析

用以上模擬數據測試高靈敏高動態環路和高靈敏環路，以13號衛星為例，以多普勒跟蹤失鎖點為性能跟蹤極限點，該點對應的動態為在該載噪比下能跟蹤的最大動態。圖5為高靈敏高動態環路跟蹤多普勒和估計的載噪比，圖6為高靈敏環路跟蹤多普勒和估計的載噪比，表4為環路跟蹤失鎖點對應的動態。

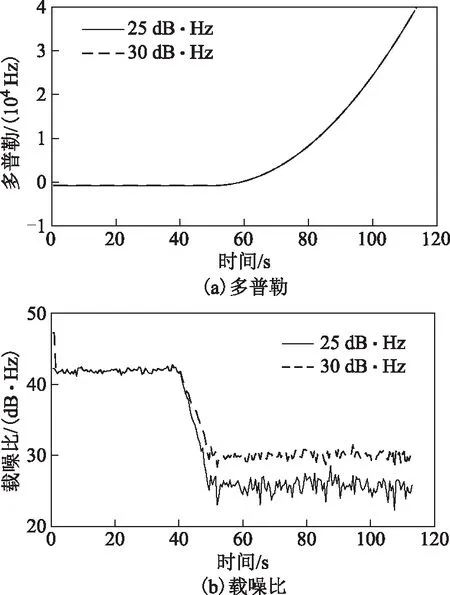
圖5 高靈敏高動態環路跟蹤多普勒和載噪比

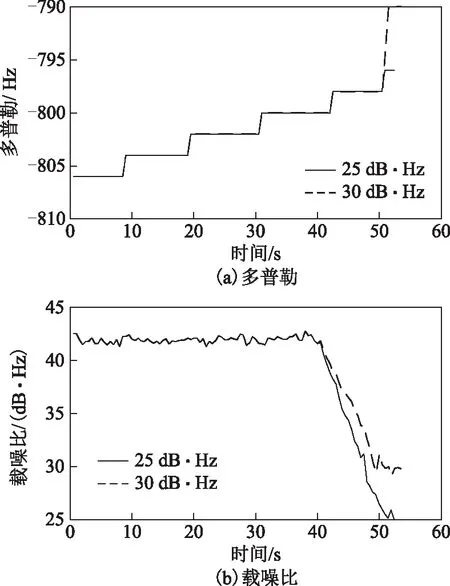
圖6 高靈敏環路跟蹤多普勒和載噪比

由圖5可知，在載噪比分別為25和30 dB·Hz的弱信號環境下，高靈敏高動態環路分別在113及113.5 s時對信號跟蹤丟失；由表4可知，此時可以跟蹤的最大加速度分別為305.1 m·s-2和317.7 m·s-2，最大速度分別為9 948和10 110.00 m·s-2。由圖6可知，在載噪比分別為25和30 dB·Hz的弱信號環境下，高靈敏環路分別在52.4和53.5 s時對信號跟蹤丟失；由表4可知，此時可以跟蹤的最大加速度分別為12和17.5 m·s-2，最大速度分別為15.0和31.5 m·s-2。2個環路對載噪比為30 dB·Hz信號的跟蹤均比為25 dB·Hz信號的跟蹤在動態性上有所提升。在相同的信號強度下，相對于高靈敏環路，高靈敏高動態環路對信號動態的跟蹤性能得到大大提升。

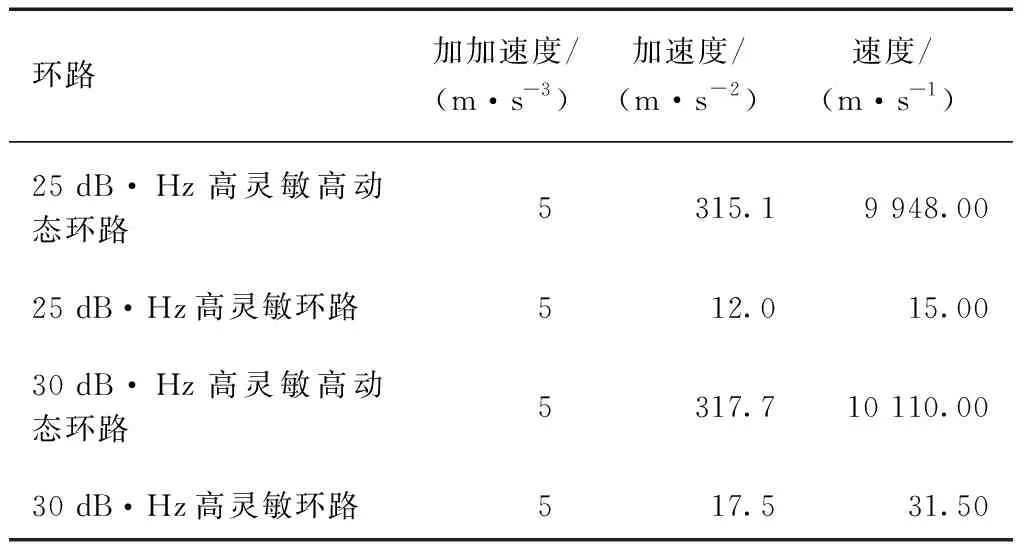
表4 高靈敏高動態環路跟蹤動態

圖7顯示FFT鑒頻器輸出最大多普勒誤差分別為4和2 Hz。

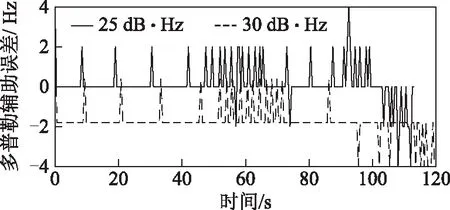
圖7 高靈敏高動態環路FFT鑒頻器輸出

2)鎖定因子分析

本文采用鎖定因子(frequency lock indicator，FLI)對INS輔助環路的算法性能進行評估。其中FLI表達式為

(6)

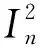
圖8所示為高靈敏高動態環路鎖定因子。由圖可以看出：在動態剛開始增加時，高靈敏環路的鎖定因子急劇下降，甚至快速失鎖；而高靈敏高動態環路跟蹤性能只是有所下降。由圖8(a)可知，在載噪比為25 dB·Hz時，高靈敏高動態環路鎖定因子平均值為0.607 5；由圖8(b)可知，在載噪比為30 dB·Hz時，高靈敏高動態環路鎖定因子平均值為0.859 2，這說明高靈敏高動態環路可以跟蹤高動態、弱信號。

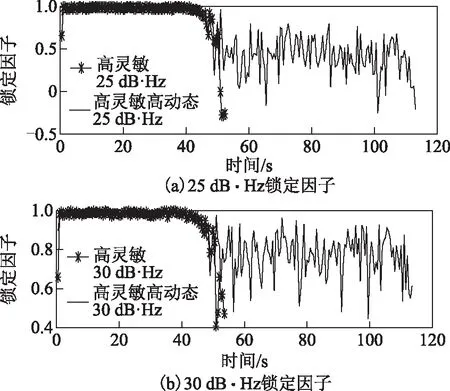
圖8 高靈敏高動態環路鎖定因子

5 結束語

本文提出了高靈敏高動態GNSS/INS超緊組合跟蹤方法。該方法利用INS和GNSS計算載體與衛星之間的多普勒變化率，并乘以輔助時間間隔來作為多普勒變化量疊加在NCO控制量上，二者混頻后，可以去除載體大部分動態，使高靈敏環路跟蹤的相當于是靜態或低動態弱信號；同時，高靈敏載波跟蹤環采用加長相干積分時間的方法提高信噪比，并采用FFT鑒別弱信號頻率，從而實現環路對高動態、弱信號的跟蹤。

經過實驗驗證及結果分析，用低精度IMU，在信號載噪比分別下降到25和30 dB·Hz后，增加信號動態，在加加速度為5 m·s-3、加速度斜升到500 m·s-2、速度增加到25 020 m·s-1的高動態、弱信號場景下，高靈敏高動態跟蹤環路可以跟蹤的最大動態性能均遠遠高于高靈敏環路的最大動態跟蹤性能；而且此時高靈敏高動態跟蹤環路FFT鑒別器輸出多普勒誤差在4 Hz以內，鎖定因子平均值分別為0.607 5和0.859 2：說明該方法可顯著提升環路的動態跟蹤性能，使得高靈敏高動態環路可以在弱信號、高動態情況下正常跟蹤。