不同飽水度紅砂巖靜態(tài)本構(gòu)關(guān)系及動態(tài)力學(xué)性能研究
鄭廣輝, 許金余,2, 王 鵬, 方新宇, 王佩璽, 聞 名
(1.空軍工程大學(xué) 機(jī)場建筑工程系,西安 710038;2.西北工業(yè)大學(xué) 力學(xué)與土木建筑學(xué)院,西安 710072))
不少學(xué)者對富水環(huán)境下巖石的靜態(tài)本構(gòu)關(guān)系和動態(tài)力學(xué)性質(zhì)進(jìn)行過試驗(yàn)及理論研究,并取得了有價(jià)值的成果,在靜態(tài)本構(gòu)關(guān)系研究方面,吳勇等[1]通過定義浸水時(shí)間為損傷因子,獲得了以浸水時(shí)間為變量的本構(gòu)關(guān)系;劉新榮等[2]研究了砂巖經(jīng)受“飽水-風(fēng)干”循環(huán)作用后抗剪強(qiáng)度的劣化規(guī)律;劉小軍等[3]考慮了水對淺變質(zhì)板巖蠕變參數(shù)的劣化效應(yīng),建立了蠕變本構(gòu)關(guān)系式。從以往含水巖石靜態(tài)本構(gòu)關(guān)系的研究中可以看出:多數(shù)研究是以巖石的某一環(huán)境要素出發(fā),如以含水率、浸水時(shí)間、飽水度等參量定義損傷因子進(jìn)行研究[4-5],鮮有研究將巖石的受荷變形作為一種損傷因子來進(jìn)行考慮,而僅將材料在力學(xué)試驗(yàn)中的響應(yīng)作為巖石力學(xué)性質(zhì)的展現(xiàn)。但事實(shí)上,巖石的損傷貫穿于其經(jīng)歷的每個(gè)階段,巖石的受荷變形也應(yīng)作為損傷累積過程被納入巖石的本構(gòu)關(guān)系當(dāng)中。
在含水孔隙類材料動態(tài)力學(xué)性能的研究方面,對含水混凝土的研究較多,也取得了不少成果[6-7],而對于含水巖石的研究還比較少,少有的含水巖石動態(tài)力學(xué)試驗(yàn)研究也局限于低應(yīng)變率或者單一含水率,如田象燕等[8]在應(yīng)變率為10-5、10-3和10-2s-1時(shí)研究了孔隙流體對巖石變形和強(qiáng)度的影響;王斌等[9]在應(yīng)變速率為100~101s-1的加載條件下研究了飽和巖石的力學(xué)性質(zhì)。
本文基于電液伺服壓力試驗(yàn)機(jī)和φ100 mm SHPB試驗(yàn)平臺,分別對不同飽水度紅砂巖試樣進(jìn)行靜態(tài)壓縮試驗(yàn)和六種沖擊彈速下的沖擊試驗(yàn),基于宏觀唯象損傷力學(xué)概念和Lemairte損傷模型,建立了紅砂巖唯象性、分段式的水軟化-應(yīng)變損傷靜態(tài)本構(gòu)關(guān)系,并利用所得本構(gòu)關(guān)系對試驗(yàn)結(jié)果進(jìn)行了合理分析;在沖擊試驗(yàn)中,研究了紅砂巖的強(qiáng)度、變形性質(zhì)與飽水度、應(yīng)變率的相關(guān)關(guān)系,探究了孔隙水-動力耦合作用對紅砂巖力學(xué)參數(shù)的影響及機(jī)理,所得成果對揭示富水環(huán)境下工程巖體災(zāi)害發(fā)生機(jī)制和防治很有意義。
1 試樣概況
飽水度表征了巖樣的吸水飽和程度,反映了含水量的多少,在一定程度上包含了巖樣的孔隙信息,是一個(gè)介于0~1之間的參數(shù),適用于工程應(yīng)用,本試驗(yàn)選用飽水度作為試樣的分類標(biāo)準(zhǔn),其計(jì)算式為:
(1)
式中:a為飽水度;m為巖樣質(zhì)量;md為干燥質(zhì)量;ms為含水質(zhì)量。
試驗(yàn)所用巖石材料為取自云南迪慶地區(qū)的新鮮紅砂巖,經(jīng)鑒定,其礦物成分包括81%石英、13%長石、3%方解石,以及少量伊利石、綠泥石和赤鐵礦;依據(jù)《GBT 50266—2013工程巖體試驗(yàn)方法標(biāo)準(zhǔn)》[10]和動態(tài)試驗(yàn)研究成果[11],分別確定靜、動態(tài)試樣尺寸為φ50 mm×100 mm和φ96 mm×48 mm,加工完成后試樣的外形、尺寸精度符合試件制備要求。

圖1 靜、動態(tài)原始試樣Fig.1 Static and dynamic original samples
試樣飽水度設(shè)定為四個(gè)等級,依據(jù)處理方法可歸類為干燥試樣、自然試樣、吸水試樣和飽水試樣;經(jīng)測量,自然狀態(tài)下試樣的平均飽水度為0.43;參照文獻(xiàn)[10]吸水性試驗(yàn)規(guī)程,將部分自然試樣置于1 071℃電熱鼓風(fēng)箱烘干24 h,制得飽水度為0的干燥試樣;將部分干燥處理后的試樣放入水槽,注水至試樣高度的1/4處,以后每隔2 h加入1/4試樣高度的水,直到試樣完全浸沒,然后任由試樣自由吸水48h,最終制得平均飽水度為0.7的吸水試樣;在水面始終高于試樣的沸煮容器內(nèi),將部分吸水試樣沸煮6 h,制得飽水度約為1的飽水試樣。
為了盡量避免偶然因素對試驗(yàn)結(jié)果造成影響,在試樣制備過程中,對巖樣進(jìn)行基本的物理、水理參數(shù)測量和原始損傷的超聲波檢測,淘汰原始參數(shù)離散性較大的試樣[12]。表1所示為試樣基本物理水理參數(shù)的平均值。
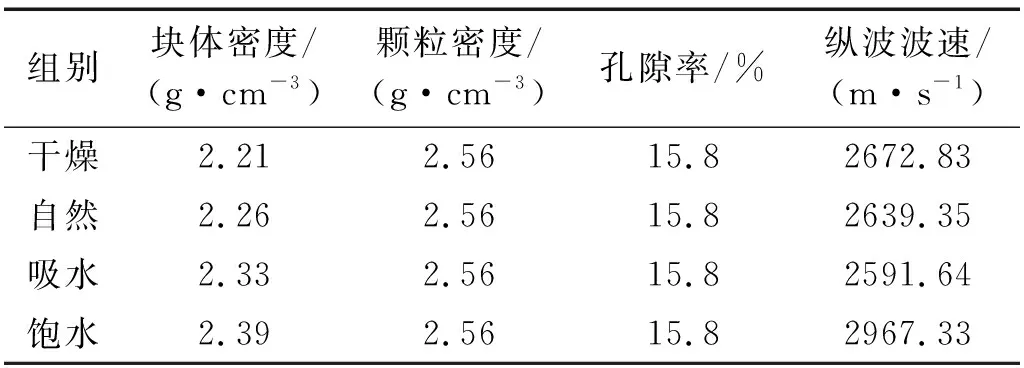
表1 試樣的基本物理參數(shù)均值
每種飽水度條件下設(shè)置3個(gè)試樣,記錄試驗(yàn)數(shù)據(jù),并進(jìn)行篩選,剔除離散性較大的數(shù)據(jù),結(jié)果取均值。從最后得到的試驗(yàn)結(jié)果來看,數(shù)據(jù)離散性小,可信度高,具有一定代表性。
2 靜態(tài)本構(gòu)關(guān)系研究
靜態(tài)壓縮試驗(yàn)是材料力學(xué)試驗(yàn)中最為常規(guī)的一種,在該試驗(yàn)條件下得到的強(qiáng)度、變形參數(shù)對巖石在各種賦存環(huán)境、加載條件下的力學(xué)性質(zhì)具有基礎(chǔ)性參考價(jià)值,因此,基于電液伺服壓力試驗(yàn)機(jī)以20 kN/min的加載方式進(jìn)行了靜態(tài)抗壓試驗(yàn)。

圖2 單軸靜態(tài)壓縮試驗(yàn)Fig.2 Uniaxial static compression test
巖石所呈現(xiàn)出的力學(xué)性質(zhì)與本身損傷的產(chǎn)生和累積密切相關(guān),分析以往巖石類材料力學(xué)性質(zhì)的研究可以得到,巖石的損傷主要發(fā)生在自然賦存階段和受荷工作階段。其中,在自然狀態(tài)下的損傷,主要指巖石在不同賦存環(huán)境下發(fā)生的物質(zhì)交換、狀態(tài)變化等引起的損傷;受荷工作狀態(tài)下的損傷,主要是指巖石承受荷載過程中發(fā)生的損傷。巖石在自然狀態(tài)下的損傷,應(yīng)側(cè)重于對材料的原始形態(tài)、基本物理參數(shù)與巖石力學(xué)參數(shù)之間關(guān)系的研究;工作狀態(tài)下的損傷,應(yīng)側(cè)重于對應(yīng)變引起的巖石損傷的研究。因此,本文將從環(huán)境因素致傷和應(yīng)變致傷兩個(gè)方面進(jìn)行不同飽水度紅砂巖的損傷本構(gòu)關(guān)系研究。
2.1 巖石的水軟化作用分析
表2為不同飽水度紅砂巖靜態(tài)壓縮彈性模量平均值,為了將飽水度與巖石的強(qiáng)度、變形性能聯(lián)系起來,進(jìn)而得出水軟化損傷變量,根據(jù)試驗(yàn)數(shù)據(jù),通過擬合得到彈性模量與飽水度的線性關(guān)系:
E(a)=6.29-2.98a,R=0.97
(2)
式中:a為飽水度。
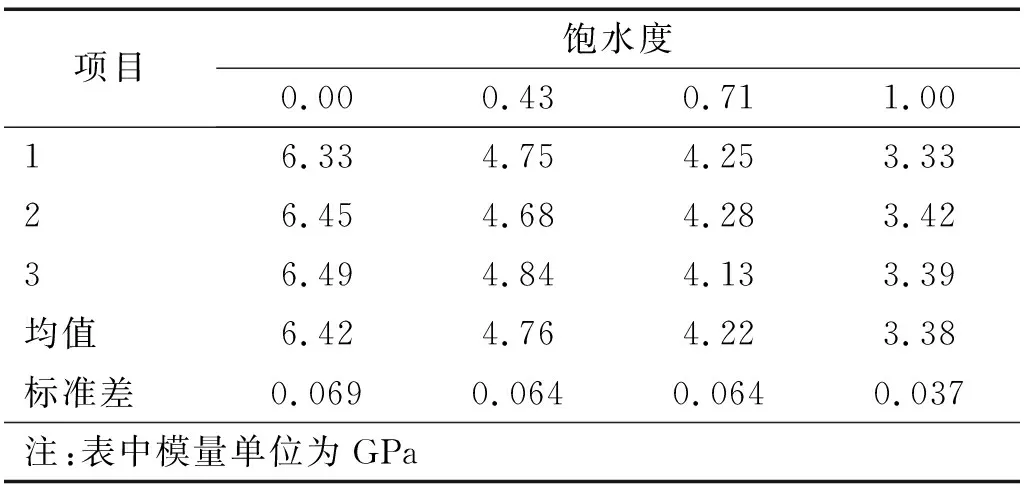
表2 不同飽水度紅砂巖彈性模量
根據(jù)宏觀唯象損傷力學(xué)概念,將水對巖石的軟化變量D(a)定義為:
D(a)=1-[E(a)/E0]
(3)
式中:E(a)為各飽水度紅砂巖彈性模量;E0為飽水度為0時(shí)的彈性模量。
由式(2)和(3)可得:
D(a)=0.022+0.463a
(4)
由式(4)可以看出,水對巖石的軟化變量隨著飽水度的增大而增大。
2.2 巖石的應(yīng)變損傷演化分析
巖石在其經(jīng)歷的每一個(gè)階段,均會發(fā)生不同程度的損傷,一般情況下,最為劇烈的損傷正是發(fā)生在承受荷載、產(chǎn)生應(yīng)變的過程中。
在實(shí)際情況下,當(dāng)巖石承受峰值應(yīng)力時(shí),巖石內(nèi)部就已經(jīng)發(fā)生了嚴(yán)重?fù)p傷,隨時(shí)會導(dǎo)致整體破壞,同樣,在液壓伺服試驗(yàn)機(jī)上進(jìn)行室內(nèi)壓縮試驗(yàn)時(shí)可以觀測到,當(dāng)荷載到達(dá)峰值應(yīng)力時(shí)試樣不僅發(fā)生劇烈變形、產(chǎn)生破壞性的開裂,同時(shí)還伴有較大的試樣碎裂的聲音,從一定意義上講,峰值應(yīng)力是試樣發(fā)生整體破壞的閾值,因此,對巖石峰前應(yīng)力-應(yīng)變曲線的研究具有重要的理論意義。從以往的研究中可以認(rèn)識到,巖石在承受峰值應(yīng)力之后仍然具有一定的承載能力,但這種承載能力是巖石結(jié)構(gòu)發(fā)生整體破壞后的性質(zhì),穩(wěn)定性差;同時(shí),基于室內(nèi)試驗(yàn)得出的應(yīng)力-應(yīng)變曲線峰前段具有巖塊整體性質(zhì),而峰后段具有碎塊集體性質(zhì),即試樣在承受峰值應(yīng)力之前是一個(gè)巖塊,而承受峰值應(yīng)力之后,試樣碎裂為多個(gè)碎塊,其表現(xiàn)出的承載能力與多碎塊之間的摩擦咬合、隨機(jī)配合有較大關(guān)聯(lián),因此,一般室內(nèi)試驗(yàn)得出的試驗(yàn)結(jié)果,對于研究巖石材料應(yīng)力-應(yīng)變峰后曲線具有較大局限性。這種多碎塊摩擦聯(lián)結(jié)屬性導(dǎo)致峰后應(yīng)力-應(yīng)變曲線受干擾因素多,趨勢多變,在進(jìn)行分析時(shí),峰后數(shù)據(jù)會對理論分析產(chǎn)生明顯影響,導(dǎo)致所得本構(gòu)理論參數(shù)對應(yīng)力-應(yīng)變曲線峰前段的擬合度降低。基于實(shí)用性和準(zhǔn)確性考慮,本文只對應(yīng)力-應(yīng)變曲線的峰前段進(jìn)行分析。
根據(jù)Lemairte損傷模型,巖石在單軸壓縮時(shí)以應(yīng)變表示的損傷演化方程可以表示為:
(5)
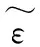
則根據(jù)一維線彈性定律和等效應(yīng)變假設(shè),考慮應(yīng)變損傷的一維線彈性定律可表示為:
(6)
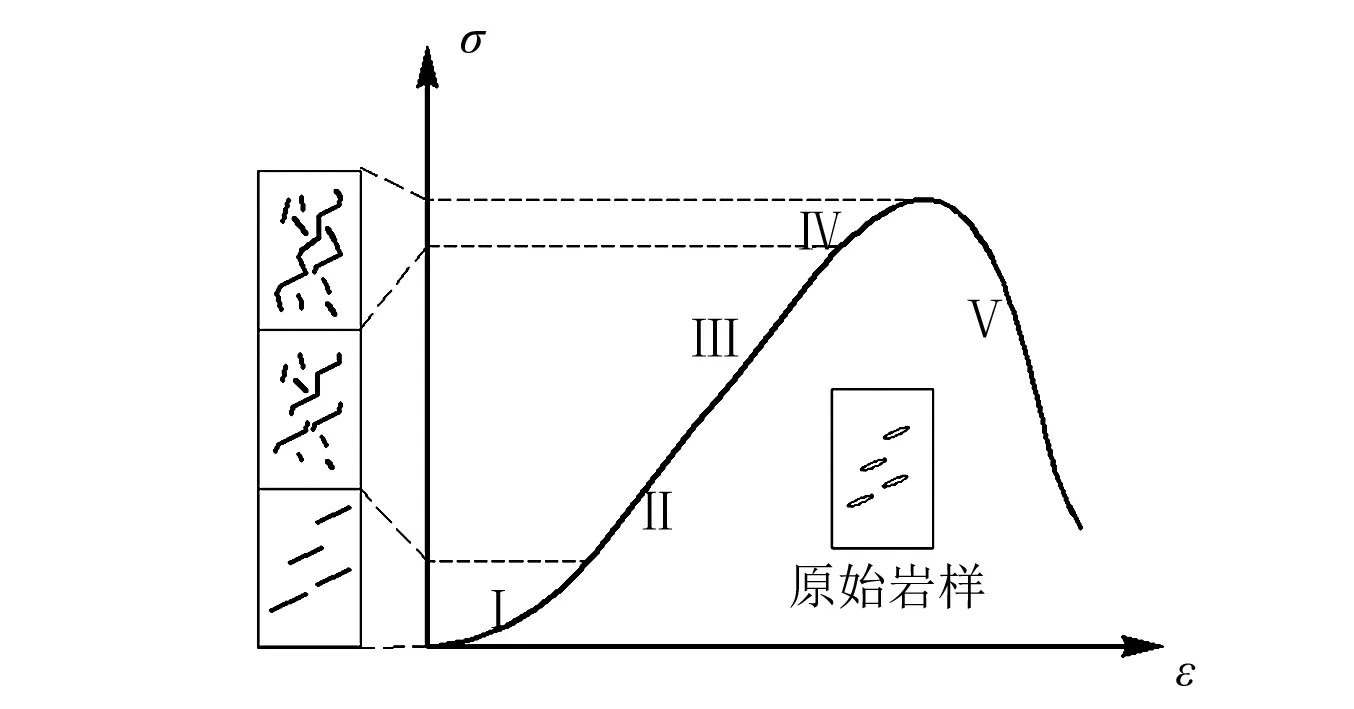
圖3 巖石應(yīng)力-應(yīng)變?nèi)€細(xì)觀機(jī)制Fig.3 Meso-mechanism of rock stress and strain curve
經(jīng)典應(yīng)力-應(yīng)變?nèi)€[13]反映了巖石類材料受荷變形過程中的一般規(guī)律(見圖3),從中分析可知,階段Ⅰ主要發(fā)生原始裂隙的擠壓閉合,階段Ⅱ主要發(fā)生材料的彈性變形,階段Ⅲ主要表現(xiàn)為微裂紋穩(wěn)定發(fā)展,階段Ⅳ主要表現(xiàn)為非穩(wěn)定破裂發(fā)展。由此可以認(rèn)為:階段Ⅰ中之所以應(yīng)變增大,主要是由于裂隙孔洞的閉合,固體結(jié)構(gòu)本身并未因應(yīng)變增加而遭受損傷,而在后續(xù)階段中,由于巖石礦物顆粒本身直接發(fā)生錯位、變形,因而導(dǎo)致?lián)p傷的產(chǎn)生。這與高瑋等[14]基于最小耗能原理得到的損傷演化結(jié)論相類似,即巖石的損傷發(fā)育存在門檻值εs,在門檻值之前,巖石處于線彈性狀態(tài),εs計(jì)算式如下:
(7)
式中:εm、σmax分別為峰值應(yīng)變和峰值應(yīng)力;Ea在原文中為損傷后彈性模量,本文取不同飽水度紅砂巖彈性模量。
基于以上分析,考慮應(yīng)變損傷的應(yīng)力-應(yīng)變關(guān)系可以表示為以下形式:
(8)
式中:εa、σa分別為裂隙擠壓閉合結(jié)束時(shí)對應(yīng)的應(yīng)變值和應(yīng)力值;εb為引起損傷的應(yīng)變,其值為ε與εa之差。
2.3 巖石的水軟化-應(yīng)變損傷本構(gòu)關(guān)系
圖4為基于電液伺服壓力試驗(yàn)機(jī),對四種飽水度紅砂巖試樣進(jìn)行單軸壓縮試驗(yàn)所得到的應(yīng)力-應(yīng)變曲線,根據(jù)前文分析,僅對峰前曲線進(jìn)行研究,即εm(1+5%)應(yīng)變段所對應(yīng)的應(yīng)力-應(yīng)變曲線,εm為峰值應(yīng)變。
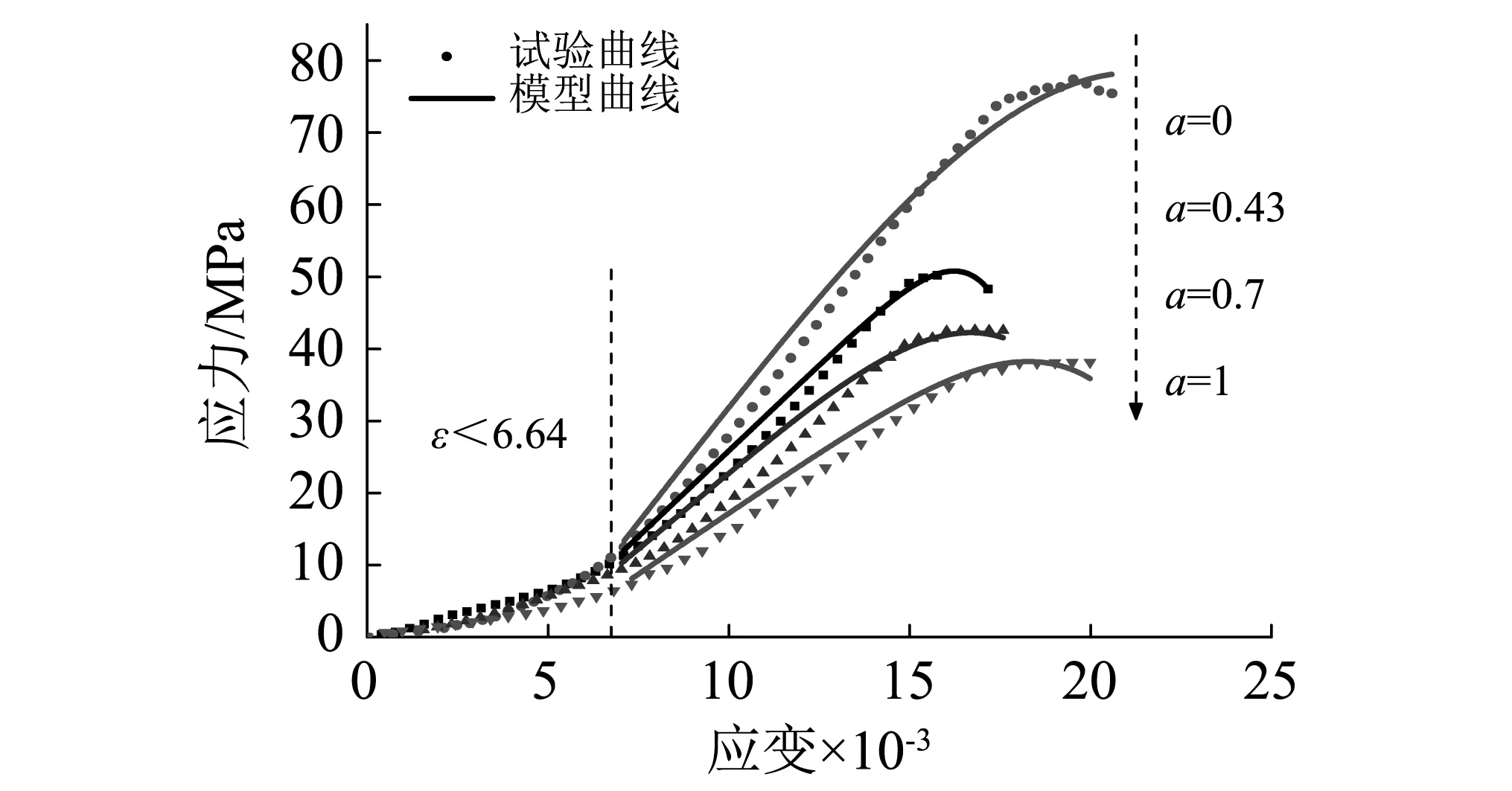
圖4 不同飽水度下紅砂巖模型曲線和試驗(yàn)曲線Fig.4 Model curve and test curveof red sandstone under different saturation
根據(jù)式(7)計(jì)算得到四種飽水度紅砂巖的損傷門檻值為3~3.7×10-3,但觀察圖2容易得到,應(yīng)力-應(yīng)變曲線在ε=6.64×10-3時(shí)存在明顯拐點(diǎn),可以認(rèn)為,在此之前試樣處在受荷變形階段Ⅰ,本著以試驗(yàn)現(xiàn)象為主的思想,加之巖石是典型的非線性、非均質(zhì)材料,在不同的賦存環(huán)境下,巖石性質(zhì)參數(shù)也存在很大差異,因此,認(rèn)為試樣應(yīng)變小于6.64×10-3時(shí),四種飽水度紅砂巖的應(yīng)力-應(yīng)變曲線可以用線性關(guān)系來近似描述;而當(dāng)應(yīng)變大于6.64×10-3時(shí),用含有應(yīng)變損傷因子的式(8)來描述應(yīng)力-應(yīng)變曲線。即本文在處理時(shí),將大于6.64×10-3的應(yīng)變視為引起巖石損傷的應(yīng)變,而不是從應(yīng)變產(chǎn)生之初就引起巖石的損傷。
因此,根據(jù)式(3)、式(5)及式(8)可以得到分段式水軟化-應(yīng)變損傷的應(yīng)力-應(yīng)變關(guān)系:
(9)
式中參數(shù)含義與前文相同。
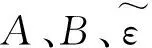
從不同飽水度紅砂巖應(yīng)力-應(yīng)變模型曲線和試驗(yàn)曲線(圖4)可以得到,本文所提出的水軟化-應(yīng)變損傷本構(gòu)關(guān)系,對實(shí)測曲線具有良好的適應(yīng)性,但由于巖石屬于典型的非線性、非均質(zhì)材料,本身具有極大的不確定性[15],僅考慮水的軟化作用和應(yīng)變損傷的本構(gòu)關(guān)系雖簡單實(shí)用,但也難以完全準(zhǔn)確地反映其力學(xué)性質(zhì),因此,在進(jìn)行數(shù)學(xué)擬合、求參時(shí)不可避免地表現(xiàn)出一定的不適應(yīng)性,即模型曲線與試驗(yàn)曲線尚存在一定偏差。
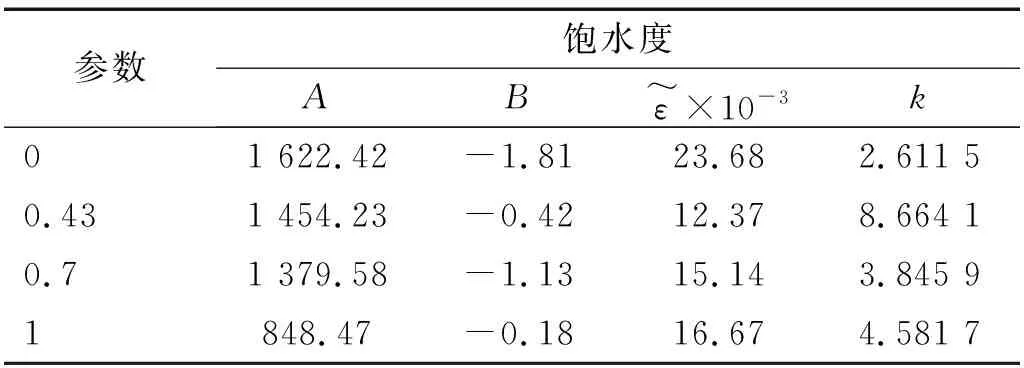
表3 不同飽和度紅砂巖本構(gòu)模型參數(shù)
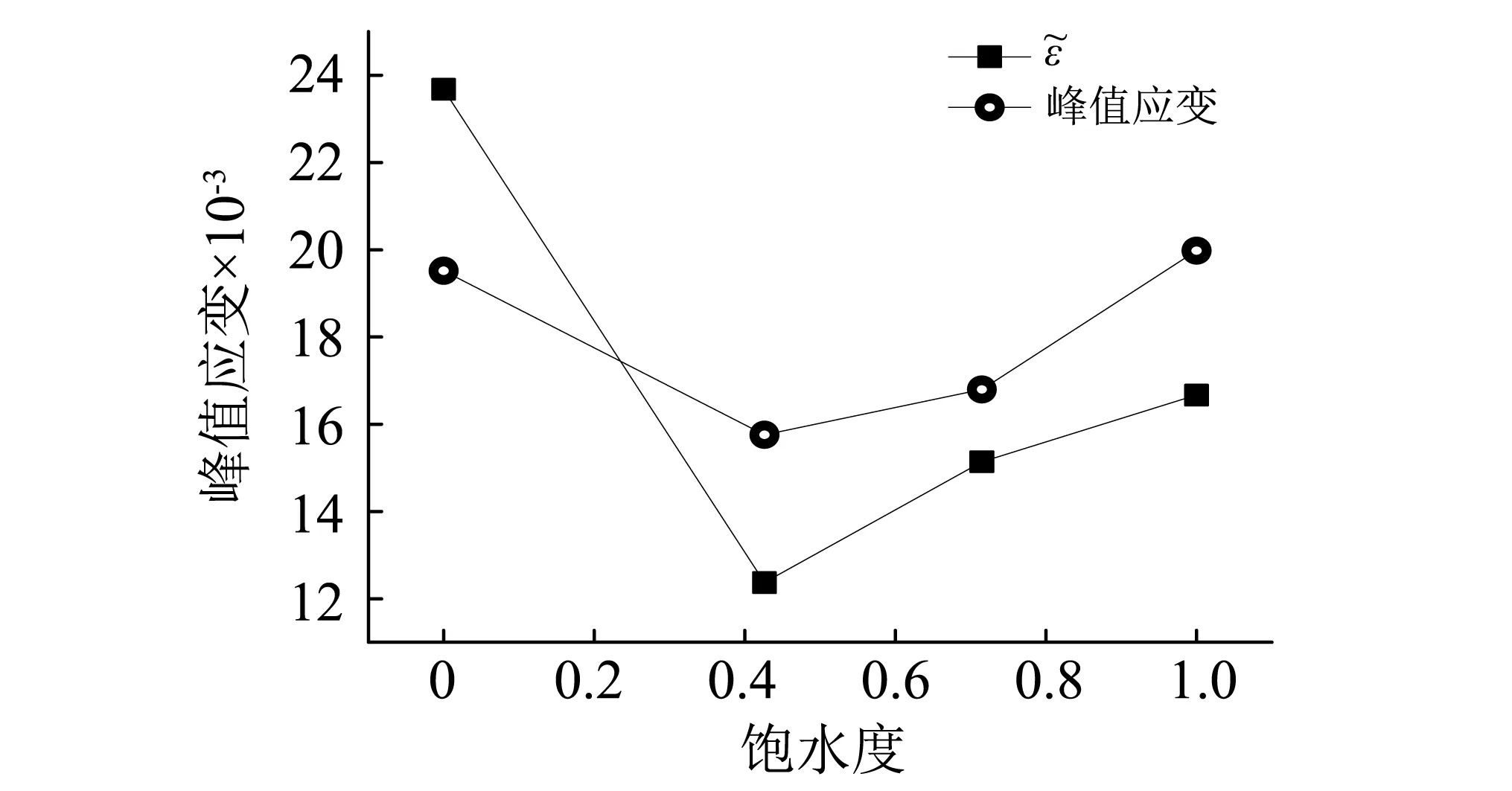
圖5 峰值應(yīng)變與隨飽水度變化趨勢Fig.5 The trend of peak stress andwith different degree of saturation
3 動態(tài)力學(xué)性能研究
沖擊試驗(yàn)在φ100 mm SHPB試驗(yàn)平臺上進(jìn)行,壓桿材料為48CrMoA高強(qiáng)度合金,彈性模量為210 GPa,泊松比為0.25~0.3,密度為7 850 kg/m3,打擊桿長0.5 m,入射桿長4.5m,透射桿長2.5 m。為減小沖擊過程中端面摩擦對試樣產(chǎn)生的類似環(huán)箍效應(yīng),在入射桿和透射桿端面均勻涂抹潤滑油薄層;在試驗(yàn)中采用波形整形技術(shù)[16],選取T2紫銅片作為波形整形材料,以保證沖擊試驗(yàn)的有效性。
沖擊作用是巖石在極短的時(shí)間內(nèi)遭受的壓縮作用,呈現(xiàn)出與靜態(tài)力學(xué)性質(zhì)的明顯差異,其中最顯著的就是力學(xué)性質(zhì)的率效應(yīng)。對于含水巖石,水對巖石既存在礦物軟化作用,又在不同應(yīng)變率下對巖石力學(xué)參數(shù)產(chǎn)生影響,有必要進(jìn)行研究討論。

圖6 φ100 mm SHPB 裝置Fig.6 SHPB test apparatus with bar of φ 100 mm
3.1 不同飽水度紅砂巖峰值應(yīng)力
從圖7(a)可以看出,在125 s-1~475 s-1應(yīng)變率范圍內(nèi),四種飽水度紅砂巖峰值應(yīng)力均隨應(yīng)變率的增大而增大;其中,隨應(yīng)變率的增大,σ0、σ0.43、σ0.71的增長速度相近,σ1的增長相對較快;當(dāng)紅砂巖的應(yīng)變率小于315 s-1時(shí),同一應(yīng)變率下σ0>σ0.43>σ0.71>σ1,當(dāng)應(yīng)變率大于315 s-1時(shí),隨著應(yīng)變率的增長,σ1接連超過σ0.71和σ0.43,但始終小于σ0。
3.2 不同飽水度紅砂巖峰值應(yīng)變
由靜壓峰值應(yīng)變與飽水度的關(guān)系(見圖5)可以發(fā)現(xiàn),在靜態(tài)壓縮條件下,ε0≈ε1>ε0.71>ε0.43;由峰值應(yīng)變-應(yīng)變率曲線圖(見圖7(b))也可得到,含水紅砂巖(a>0)在同一應(yīng)變率下的峰值應(yīng)變呈現(xiàn)出與靜態(tài)試驗(yàn)相一致的現(xiàn)象,即峰值應(yīng)變隨飽水度的增大而增大ε1>ε0.71>ε0.43,但隨著應(yīng)變率的增大,干燥紅砂巖(a=0)的峰值應(yīng)變逐漸小于含水試樣(a>0)。同時(shí)還可以得到,無論是否含水,同一飽水度試樣的峰值應(yīng)變均隨著應(yīng)變率的增大而增長,呈現(xiàn)出明顯的應(yīng)變率效應(yīng)。
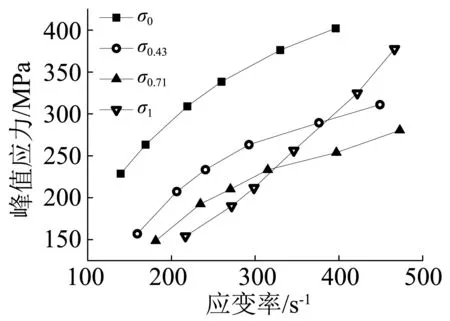
(a)峰值應(yīng)力-應(yīng)變率

(b)峰值應(yīng)變-應(yīng)變率
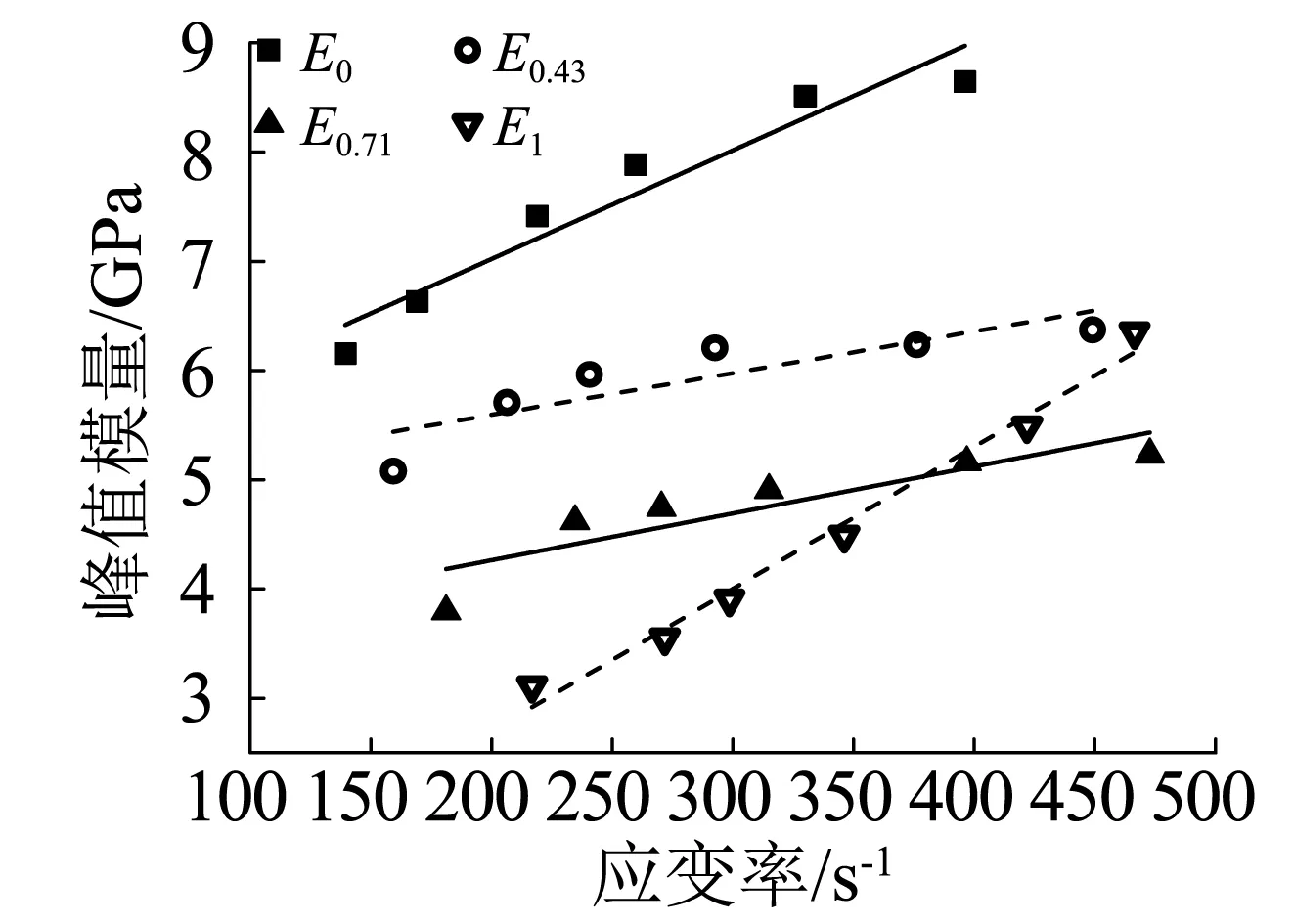
(c)峰值模量-應(yīng)變率
3.3 不同飽水度紅砂巖峰值模量
沖擊作用對巖石的損傷發(fā)生在極短的時(shí)間內(nèi),屬于瞬間性質(zhì)的破壞,一般為不可恢復(fù)過程,由于沖擊試驗(yàn)應(yīng)力-應(yīng)變曲線存在較大波動,根據(jù)彈性模量的計(jì)算方法[10](見圖8),導(dǎo)致彈性模量取值也存在很大的不確定性,另一方面,如圖8所示,峰值模量表征裂隙壓密階段Ⅰ、彈性變形階段Ⅱ、微裂紋穩(wěn)定發(fā)展階段Ⅲ和非穩(wěn)定破裂發(fā)展階段Ⅳ總體的變形難易程度,更能反映材料在喪失整體承載能力之前抵抗變形的能力,因此,沖擊作用下峰值模量比彈性模量更具有研究價(jià)值。
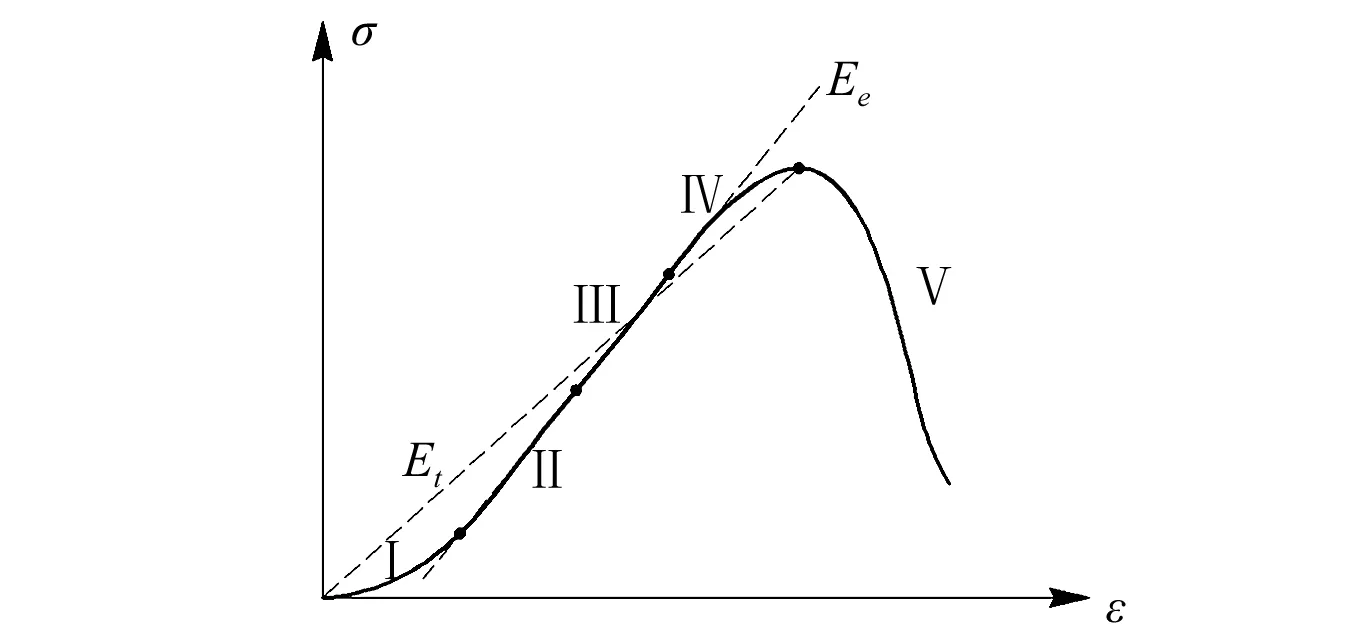
圖8 峰值模量與彈性模量計(jì)算方法(Et、Ee分別表示峰值模量和彈性模量)Fig.8 Calculation method of peak modulus and elastic modulus
圖7(c)為不同飽水度下峰值模量與應(yīng)變率的關(guān)系曲線,其中飽水度為1的試樣的峰值模量增長最快,在同一種飽水度下,峰值模量均隨著應(yīng)變率的增長而增長,可以用線性關(guān)系進(jìn)行描述:
(12)
3.4 不同飽水度紅砂巖沖擊力學(xué)性質(zhì)分析
當(dāng)應(yīng)變率較低時(shí),試驗(yàn)所得力學(xué)參數(shù)更多地反映巖石基本物理力學(xué)性質(zhì),而隨著應(yīng)變率的逐漸增大,孔隙水、孔隙結(jié)構(gòu)以及材料基體之間的耦合作用將發(fā)生一系列變化,結(jié)合以上試驗(yàn)現(xiàn)象,具體分析是由于:
(1)水對紅砂巖的軟化作用隨著飽水度的升高而愈加明顯,但當(dāng)應(yīng)變率較高時(shí),試樣孔隙水將產(chǎn)生黏結(jié)力F[7](見(式10))和Stefan效應(yīng)阻力F′[6](見式(11)),由式(10)、(11)可知,孔隙水體積越大,則黏聚力越強(qiáng),而材料應(yīng)變率越大,Stefan效應(yīng)引發(fā)的抑裂阻力越大,抑制了損傷的發(fā)育,從而影響了巖石的強(qiáng)度、變形性質(zhì);
(10)
式中:V為孔隙液體體積;γ為表面能;ρ為水的彎月面半徑;θ為濕潤角。
(11)
式中:η為裂隙液體黏度;r為中間充盈有黏性液體的兩圓形平板的半徑;v為圓形平板抽離的相對速度;h為兩圓形平板的間距。
(2)在水-巖-力的響應(yīng)體系中,既存在水對巖石的軟化作用,同時(shí)也存在應(yīng)變率、孔隙水、巖石結(jié)構(gòu)之間的動力耦合強(qiáng)化反應(yīng),這兩種作用始終存在,但隨著應(yīng)變率的變化,兩種作用的效能發(fā)揮有所浮動,因此出現(xiàn)了以上試驗(yàn)現(xiàn)象,即:對于峰值應(yīng)力和峰值模量,在飽水度為0.71之前,水的軟化作用更為明顯,而當(dāng)飽水度為1時(shí),耦合強(qiáng)化作用逐漸加強(qiáng);對于峰值應(yīng)變,在同一應(yīng)變率下,水對巖石的軟化作用相對于應(yīng)變率較小時(shí)更加明顯,導(dǎo)致試樣更加容易變形。
4 結(jié) 論
通過探究飽水度與彈性模量的關(guān)系,得出與飽水度相關(guān)的軟化變量,基于Lemairte損傷模型,引進(jìn)巖石的應(yīng)變損傷因子,之后得到靜態(tài)壓縮狀態(tài)下,紅砂巖分段式水軟化-應(yīng)變損傷本構(gòu)關(guān)系,最后利用所得本構(gòu)關(guān)系,對不同飽水度紅砂巖靜態(tài)壓縮試驗(yàn)結(jié)果進(jìn)行了合理分析;對四種飽水度紅砂巖進(jìn)行不同應(yīng)變率下的沖擊試驗(yàn),探究了不同飽水度紅砂巖力學(xué)性質(zhì)的應(yīng)變率效應(yīng)及其機(jī)理,主要結(jié)論如下:
(1)以彈性模量為衡量標(biāo)準(zhǔn),水對紅砂巖的軟化作用隨著飽水度的增大而增大。
(2)在應(yīng)變小于6.64×10-3時(shí),試樣原始裂隙擠壓閉合,材料本身并未因應(yīng)變增加而發(fā)生損傷,在后續(xù)加載中,巖石礦物顆粒本身直接發(fā)生變形,導(dǎo)致?lián)p傷的產(chǎn)生,基于此結(jié)論得出的分段式水軟化-應(yīng)變損傷本構(gòu)關(guān)系具有良好的適應(yīng)性。
(4)各飽水度紅砂巖均呈現(xiàn)出明顯的應(yīng)變率效應(yīng),峰值應(yīng)力、峰值應(yīng)變和峰值模量均隨應(yīng)變率增大而增大。
(5)在水-巖-力的響應(yīng)體系中,水對巖石的軟化作用和應(yīng)變率、孔隙水、巖石結(jié)構(gòu)之間的動力耦合強(qiáng)化作用始終存在,但隨著應(yīng)變率的變化,兩種效能的體現(xiàn)有所浮動,進(jìn)而影響紅砂巖性能。

