基于ABAQUS的抗滑樁加固邊坡的數值模擬分析
曾 晉
(成都理工大學 工程技術學院,四川 樂山 614000)
滑坡不僅會對農業生產、建筑物造成經濟損失,同時也會造成人員傷亡,因此對邊坡穩定性的研究一直受到工程和學術界的廣泛關注。目前,主要通過排水措施、削坡減載,填土、錨桿支護、支擋結構、抗滑樁等方式對邊坡進行加固分析。經過長時間的研究和論證,發現抗滑樁對邊坡進行加固具有較大的優勢,但是目前對于抗滑樁加固邊坡的研究剛剛起步,并且各個學者研究的結果也不盡相同。因此,本文基于ABAQUS軟件采用強度折減法對抗滑樁加固邊坡進行模擬分析,研究樁位、樁間距與樁徑比、樁長等因素對邊坡安全系數以及邊坡失穩時滑裂面出現位置的影響。
1 邊坡土體的數值模型理論分析
本文基于強度折減法和極限平衡方法分析土質邊坡,通過有限元軟件ABAQUS進行邊坡的穩定性分析,利用ABAQUS提供的彈塑性理論模型和屈服準則判斷不同屈服準則下的安全系數。數值計算方法可以分析不同影響因素對邊坡穩定性的影響,不僅可以定性研究邊坡穩定性問題,也能夠進行一定的定量分析。隨著計算機技術的快速發展,采用數值分析方法對邊坡穩定問題進行研究也有了長足的進步。見圖1。
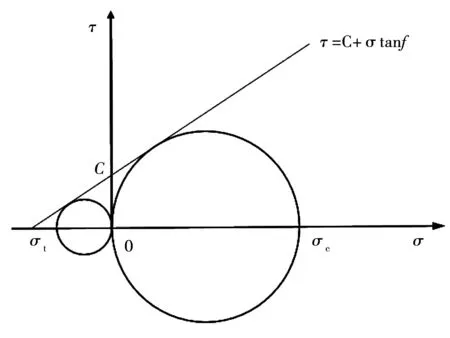
圖1 有效莫爾應力圓
ABAQUS提供了多種土體本構模型,其中摩爾-庫倫本構模型主要考慮不光滑小表面的情況,較為真實反映了土體的應力-應變的特點。通過大量的試驗研究表明,圖1為可以用有效應力表示土體破壞的莫爾應力圓,莫爾圓公切線為一條直線,這條直線的公切線被稱為莫爾-庫倫破壞準則,其表達式如下:
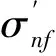
根據圖1中幾何關系,得到如下式:
上式中的莫爾-庫倫破壞準則在M-C模型中用作屈服函數,該函數為一個不規則的六凌錐,見圖2。
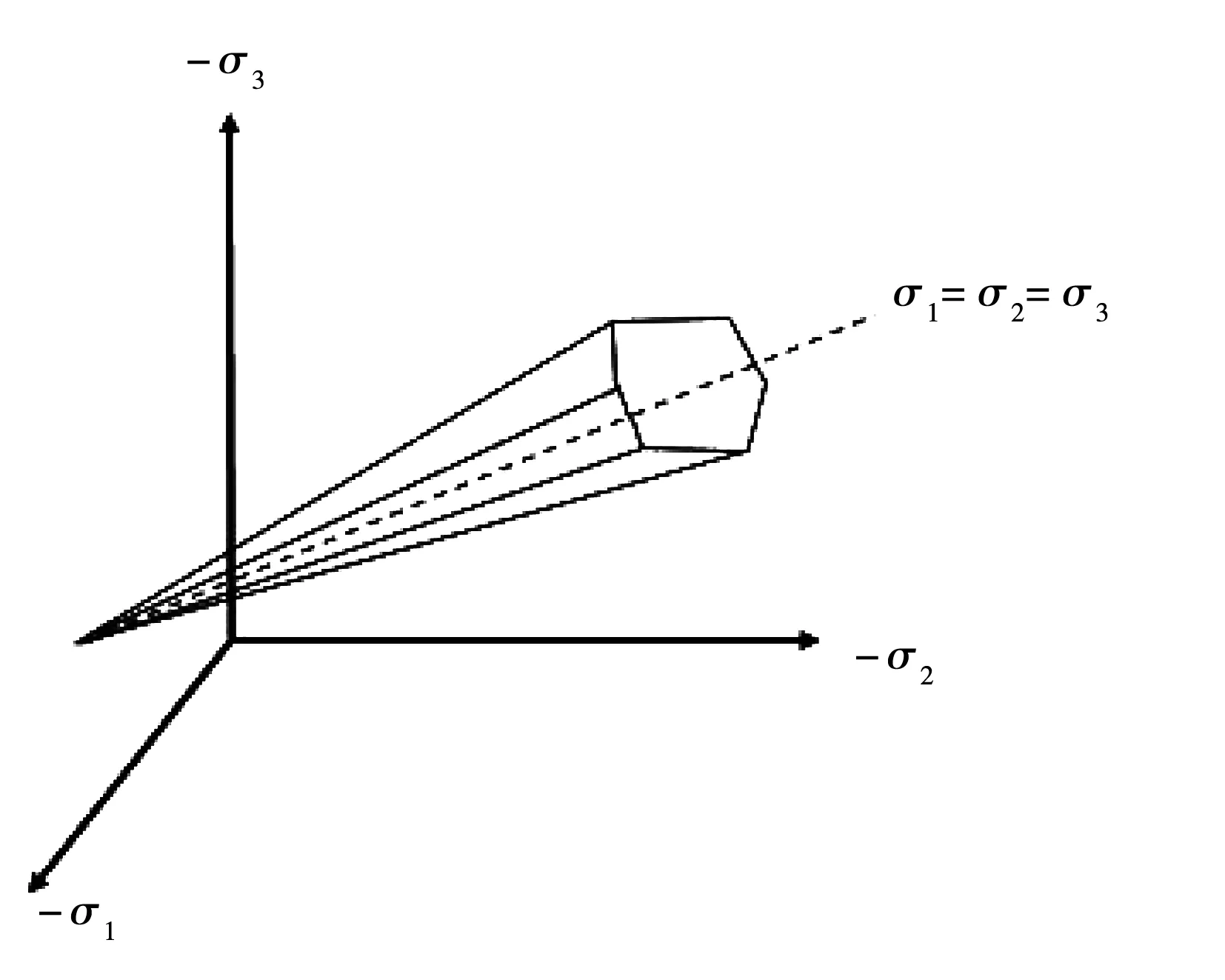
圖2 M-C屈服面
有效主應力通過不變量表示如下:
2 數值模型
根據工程實例,對均質黏性土邊坡進行幾何模型建立,根據試驗和規范得到土體的計算參數見表1。

表1 土體參數表
數值計算模型見圖3。模型尺寸為:邊坡的前緣長和高度分別為L1=30 m,H1=42 m;邊坡的坡體在水平投影長度L2=24 m,坡體后緣長度為L3=45 m,邊坡前后、左右4個面進行法向位移約束,底面進行3個方向的全約束,土體選用理想彈塑性本構模型進行分析。
圖3 邊坡土體的計算模型
3 抗滑樁數值模擬結果分析
3.1 最優樁位和合理樁間距的確定
由于邊坡加固的復雜性,運用抗滑樁對邊坡進行加固,加固的最優位置以及合理間距具有較大的差異。不同學者的研究具有不同的結果,還未達到統一的判斷標準,因此對抗滑樁的加固位置以及合理間距進行研究具有重要的意義。通過控制樁間距S與樁阻滑邊B的比值分別為1、2、3、4、5和6來改變抗滑樁在坡體中的位置,采用ABAQUS軟件的強度折減方法,自動搜索邊坡的安全系數,得到邊坡的整體安全系數,見圖4。
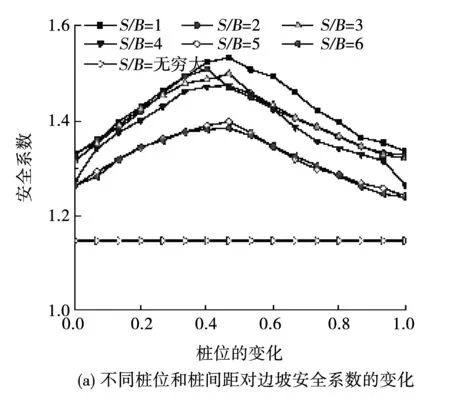
圖4不同影響因素與安全系數的關系
由圖4可知,當樁位位于邊坡中部往下位置時,安全系數迅速增加,這主要是抗滑樁的加固起到了一定的作用。通過對圖4曲線進行擬合,得到二次曲線方程,進一步探究最大安全系數的具體位置。見表2。
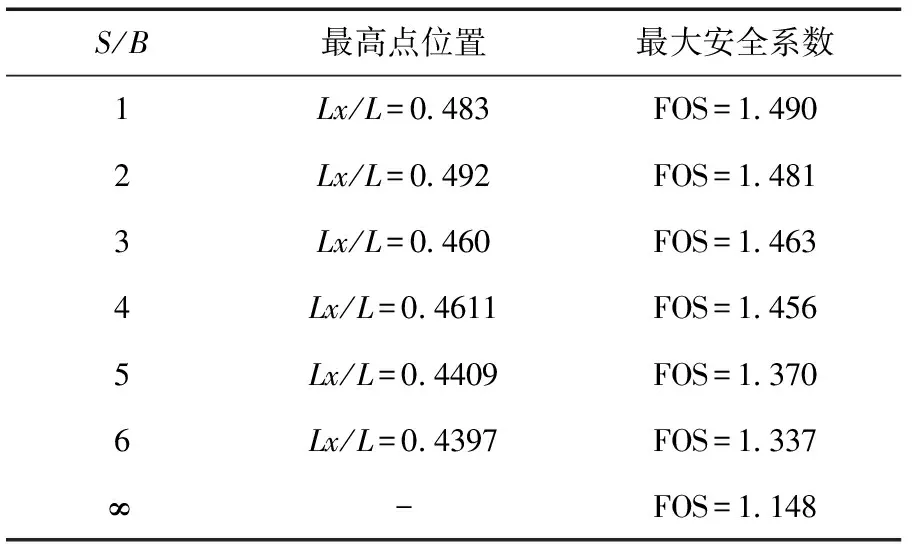
表2 不同S/B下最大安全系數表
根據以上擬合分析可知,當S/B=1~4時,邊坡的最大安全系數接近坡中;隨著S/B的減小,這個現象越明顯。隨著S/B的增大,邊坡的安全系數逐漸降低,邊坡樁的最大安全系數位置向下移動;當S/B增大到一定程度時,近似認為邊坡處于無樁加固狀態,此時邊坡及其不穩定,極易出現失穩等情況。不論加固樁處于什么位置時,安全系數隨樁間距和S/B的增大而減小,現取S/B=2不同樁位出現塑性變形圖進行分析。見圖5~圖6。
圖5為抗滑樁位于斜坡下半部分時的塑性變形圖,圖6為抗滑樁位于斜坡上半部分時的塑性變形圖。由圖5~圖6可知,當抗滑樁位于Lx/L=0~1時,坡體出現臨界的滑裂面,以抗滑樁為界將坡體分為兩個部分,當抗滑樁與處于中間位置時,邊坡產生的塑性變形最小,此時抗滑樁的阻滑效果更為有效。當抗滑樁位于坡腳或者坡頂附近時,邊坡的塑性區滑裂面基本上呈一條圓弧形曲面分布,此時抗滑樁的阻滑效果與無抗滑樁的邊坡非常接近。因此,在僅僅考慮邊坡的安全性,抗滑樁的最優加固位置Lx/L=0.4左右,此時的邊坡的加固效果最佳。但在工程中不僅要考慮到安全性,同時也要考慮到經濟、資源配置等因素,通過結合以上分析,最優加固位置Lx/L=0.2~0.4處,綜合邊坡加固效果最佳。

圖5 抗滑樁位于斜坡下半部分的塑性變形圖

圖6 抗滑樁位于斜坡上半部分的塑性變形圖
3.2 不同樁長結果
根據3.1節的分析可知,抗滑樁位于邊坡的最優位置Lx/L=0.4處,保證樁的橫截面積和樁間距相同的情況下,改變抗滑樁的長度分別為6、10、14、16、18、22和26 m共6組進行對比分析,樁長對邊坡安全系數及塑性變形滑裂面的影響見圖7。
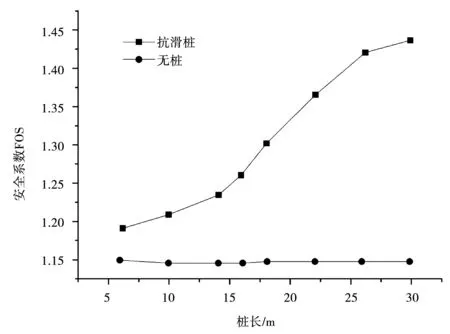
圖7 加固樁長與邊坡安全系數的變化關系
由圖8可知,抗滑樁長度Lp<16 m時,邊坡塑性滑裂面均完全包裹住抗滑樁,此時抗滑樁對邊坡的抗滑效果非常差,邊坡的抗滑性能相當于無抗滑樁加固狀態下的邊坡的抗滑性能,這一點從邊坡的安全系數就可以看出,抗滑樁長度小于16 m時的安全系數跟無抗滑樁加固的邊坡的安全系數較為接近。當抗滑樁長度在16~18 m時,邊坡的塑性滑裂面恰好沒有通過抗滑樁底,并且滑移線沒有向下移動,其安全系數速速上升,此時抗滑樁的抵抗滑移效果非常明顯,抗滑樁樁底位于滑移線以下,因此此時抗滑樁具有一定的錨固作用。
由圖7可知抗滑樁的長度與邊坡安全系數呈現分段線性關系,當抗滑樁長度在0~16 m時,線性增長速度極小;當抗滑樁長度在16~18 m時,安全系數發生突變;抗滑樁長度在18~30 m時,安全系數進一步增大。但是相對16~18 m時較緩一些。

圖8 不同抗滑樁長度下斜坡上半部分的塑性變形圖
由圖7和圖8可知,抗滑樁長度在16~26 m時,邊坡的安全系數增長明顯,隨著長度的繼續增加,邊坡的安全系數增加非常緩慢。這主要是抗滑樁的長度達到一定程度之后它的抗滑能力達到最大,隨著抗滑樁長度的繼續增大,土體的抗剪強度降低,抗滑樁的側壓力會增大,因此樁體可能發生破壞,進而導致邊坡的安全系數增加并不明顯。通過以上分析可知,抗滑樁長度在22~26 m較為合適,抗滑樁的錨固深度為4/11~5/13樁長較為合理。
4 結 論
本文通過ABAQUS數值計算對抗滑樁加固邊坡的最優樁位、樁間距和樁長進行了模擬分析,結論如下:
1) 當樁間距S與樁阻滑邊B比值為1~4時,邊坡的最大安全系數接近坡中;隨著S/B的增大,邊坡的安全系數逐漸降低,邊坡樁的最大安全系數位置向下移動;當S/B增大到一定程度時,近似認為邊坡處于無樁加固狀態,此時邊坡及其不穩定,極易出現失穩等情況,不論加固樁處于什么位置時,安全系數隨樁間距和S/B的增大而減小。
2) 在僅僅考慮邊坡的安全性,抗滑樁的最優加固位置Lx/L=0.4左右,此時的邊坡的加固效果最佳。但是在工程中不僅要考慮到安全性,同時也要考慮到經濟、資源配置等因素,通過結合以上分析,最優加固位置Lx/L=0.2~0.4處,綜合邊坡加固效果最佳。
3) 當抗滑樁長度在0~16 m時,線性增長速度極小;當抗滑樁長度在16~18 m時,安全系數發生突變;抗滑樁長度在18~30 m時,安全系數進一步增大,但是相對16~18 m時較緩一些。抗滑樁長度在22~26 m較為合適,抗滑樁的錨固深度為4/11~5/13樁長較為合理。

