基于最小Tsallis交叉熵改進型PCNN圖像分割算法

李東興,張 起,高倩倩,吳秀東,蔡亞南

(山東理工大學 機械工程學院，山東 淄博 255049)

隨著生物視覺的發展，脈沖耦合神經網絡(PCNN)[1]以其獨有的生物視覺特性受到越來越多學者的關注，被譽為“第三代神經網絡”，并在圖像增強、目標識別、邊緣檢測、圖像融合和圖像分割等領域得到了很好的應用[2-5].

在圖像分割應用方面，PCNN可以較好地分離目標和背景部分的重疊，也能處理目標內部較小的灰度變化和空間不連貫等問題.與傳統神經網絡相比，不需要預先選擇需要處理的空間范圍，但是它需要人工設置各種門限參數、衰減時間常數、加權因子及連接系數等，要通過合理設置循環迭代次數，才能得到最佳分割效果.為此，近年來眾多學者研究出一些參數簡化的PCNN模型，使得模型通用性得到了很好的保障.如Lu等提出了一種基于區域生長的簡化PCNN的圖像分割新方法，通過修改鏈接通道函數和降低參數調整的復雜度來實現[6]；楊娜等提出了基于改進的脈沖耦合神經網絡模型的圖像分割，通過感受野模型優化鏈接矩陣，使PCNN模型具有方向性和尺度性[7]；Gao等提出了自適應脈沖耦合神經網絡參數的圖像分割方法，可以直接從圖像統計中獲取鏈接系數全局和局部值和神經元的初始點火閾值[8]；鄭欣等提出了基于活躍度的脈沖耦合神經網絡圖像分割方法，將圖像劃分為內部復雜程度相近的子塊，利用其提出的局部圖像活躍度(ADLA)指標對不同子塊自適應地確定PCNN模型參數[9].

這些研究方法的提出都可以在一定程度上簡化PCNN模型，使得模型具有一定的自適應性，但都很難避免其鄰域的抑制作用以及閾值設置的指數衰減特性和周期震蕩特性，并且循環運算迭代次數無法準確確定，從而很難選擇最優分割結果，造成這些算法的局限性. 因此，本文提出一種基于最小Tsallis交叉熵改進型PCNN圖像分割算法，以期有效簡化PCNN模型，實現圖像的自動分割.

1 最小Tsallis交叉熵

最小Tsallis交叉熵將圖像的像素視為隨機變量，利用最小Tsallis交叉熵準則來選擇閾值，使得原始圖像和分割圖像之間的信息差異最小，這種方法在閾值選擇過程中充分考慮目標和背景之間的信息量差異和二者之間的相互關系，保證閾值的恰當選擇. 該算法的描述如下：

設P={pi}是一個離散的概率分布，且0≤pi≤1，該分布的Tsallis熵[10]定義為

(1)

式中，c表示一個待定系數，用來描述非廣延性，通常取值0.8. 由于Tsallis熵具有非廣延性或非可加性，所以對一個可分解為統計獨立的兩個子系統A和B而言，其Tsallis熵可以表示為

Sc(A+B)=Sc(A)+Sc(B)+

(1-c)Sc(A)Sc(B)

(2)

Tsallis熵充分考慮了兩個子系統之間的相互關系. 根據圖像中存在的非可加信息，Tsallis交叉熵的定義如下：

(3)

假設I是待分割圖像，其直方圖R={r1,r2,…,rN}，并假設分割后圖像的直方圖為Q={q1,q2,…,qN}. 假設閾值t將目標圖像I分割為目標A和背景B兩部分，則根據公式(3)的Tsallis交叉熵的形式，目標A像素間的Tsallis交叉熵定義為

(4)

背景B像素間的Tsallis交叉熵定義公式為

(5)

根據Tsallis熵的非廣延性，二值化時定義R和Q的Tsallis交叉熵是目標A像素間的Tsallis交叉熵和背景B像素間的Tsallis交叉熵之和，即圖像分割前后總的Tsallis交叉熵定義為

(6)

則尋找PCNN最佳迭代次數的過程即是最小化D(R∶Q∶t)的過程，當D(R∶Q∶t)取得最小值時，PCNN迭代過程終止，獲得最優分割圖像.

其中公式(3)～(6)中分割后圖像直方圖的概率分布Q是未知的，本文以混合均勻分布估計Q，即假設由待選閾值t分割后得到的Q中的目標和背景灰度均勻，其估計表達式為

(7)

式中:L表示圖像灰度上界;h(i)表示待分割圖像I的直方圖.

2 PCNN改進模型及圖像分割

2.1 PCNN模型的基本原理

20世紀90年代，Gray和Eckhorn等基于哺乳動物的視覺區神經元的特性研究提出了PCNN. 在傳統PCNN模型[11]中，單個神經元由接收、調制和脈沖產生3個部分組成，并用下面的離散方程來描述：

Fij(n)=e(-αF)Fij(n-1)+

(8)

Lij(n)=e(-αL)Lij(n-1)+

(9)

Uij(n)=Fij(n)+[1+βFij(n)]

(10)

Eij(n)=e(-αE)Eij(n-1)+VEYij(n-1)

(11)

(12)

對于二維圖像，圖像中的每個像素與PCNN網絡的神經元一一對應，并且圖像像素的灰度值Iij作為對應神經元的輸入. 每個神經元和鄰近的神經元相連，Mijkl和Wijkl決定其鏈接強度的大小. 每個神經元的輸出對其鄰域中的其他神經元的作用只有兩種狀態：激發和抑制(或者點火和不點火). 當鏈接矩陣Mijkl和Wijkl所在的鄰域中存在與Iij灰度級相近的像素值時，如果此時某個神經元點火成功，將會引起其鄰域內與其灰度值相近的其他神經元集體點火，由此產生了脈沖序列輸出Y(n).

2.2 改進PCNN模型

傳統PCNN模型過于復雜，包含9個待定的模型參數，需要人工設定循環迭代次數，其圖像分割結果具有很強的依賴性. 為此，本文根據現有的簡化PCNN模型進行改進，實現自適應獲取鏈接系數β和鏈接權值矩陣Wijkl，改進內部活動項Uij(n)和閾值函數Eij(n)，自動獲取循環迭代次數，最終進行自適應圖像分割. 改進的PCNN模型如下：

Fij(n)=Iij

(13)

(14)

由于灰度值大的像素先點火，然后刺激其鄰域像素提前點火，灰度值較小的像素本身點火就晚，且對其鄰域的像素起反作用，所以這里引入抑制輸入項Hij(n)對內部活動項進行改進.

Uij(n)=Fij(n)[1+βLij(n)][1-γHij(n)]

(15)

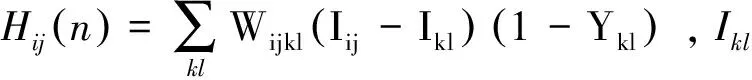
(16)

閾值衰減函數按指數變化，雖然符合人眼對亮度強度響應的非線性特性，但在計算時需要將時間劃分為離散的時間段，這將直接影響運行速度和分割結果.

采用以下方式獲取動態閾值[12]：

Eij(n)=VEHε(Fij-m0(n))

(17)

改進的PCNN模型直接消除式(8)～(11)的指數衰減項，減少數學分析的復雜度.而且該方法只考慮鏈接輸入鄰域對中心神經元的影響，不考慮反饋輸入鄰域. 所以，神經元的反饋輸入就是其外部刺激，對應二維圖像中每個像素的灰度值；鏈接輸入就是神經元的鄰域輸入，通常取3×3鄰域.

為了更好地分割圖像，必須對鏈接權值矩陣Wijkl和鏈接系數β參數進行有效設置.

(1)鏈接權值矩陣Wijkl是鄰域神經元對中心神經元的激勵程度，表示鄰域神經元對中心神經元傳遞信息的強弱，一般按照距離中心神經元越近權值越大的原則取值. 本文采用非線性各向異性擴散模板，該模板在正確描述鄰域神經元對中心神經元激勵程度的同時，還具有平滑噪聲和平滑邊緣細節的效果，其表達式為

(18)

式中:▽F(i,j)為神經元(i,j)在鄰域的梯度值；k為非線性各向異性擴散噪聲系數.

(2)鏈接系數β表示PCNN網絡內部神經元之間的耦合鏈接程度，其值越大，鏈接強度越大，可以同步點火的神經元就越多. 本文采用當前神經元鄰域內所有神經元灰度值的均方差獲取該參數，其表達式為

(19)

圖像分割的流程圖如圖1所示，具體實現步驟如下：

步驟1對輸入的圖像進行歸一化操作，初始時所有的神經元都未點火，設置PCNN初始參數，Fij[0]=Lij[0]=Uij[0]=Yij[0]=Eij[0]=0，計算圖像的初始閾值.

步驟2優化計算PCNN網絡中各神經元之間的鏈接系數β和鏈接權值矩陣Wijkl.

步驟3啟動耦合連接PCNN網絡，將圖像像素作為外部激勵，利用式(13)～(17)進行圖像分割的迭代.

步驟4計算每次迭代時輸出圖像的Tsallis交叉熵值，若此次迭代取得最小Tsallis交叉熵值，迭代停止，n為最優迭代次數，該狀態下得到的圖像分割效果最為理想.

步驟5運用雙邊濾波[13]對分割后的圖像進行濾波處理.

圖1 圖像分割流程圖Fig.1 Flow chart of image segmentation

3 實驗

為了驗證本文算法的可行性，對上述算法進行仿真實驗.選用大小為256×256灰度級的Lena和Cameraman圖像，并且依次選用文獻[6]～文獻[9]算法和本文算法進行圖像分割，其中Lena圖像分割效果如圖2所示，Cameraman圖像分割效果如圖3所示.

(a)原始圖像 (b)文獻[6] (c)文獻[7]

(d)文獻[8] (e)文獻[9] (f)本文算法圖2 Lena圖像分割效果Fig.2 Lena image segmentation results

根據圖2和圖3的圖像分割效果圖可以看出，本文算法明顯優于各參考文獻算法. 對于Lena圖像，文獻[6]和文獻[7]存在欠分割現象，且易形成偽邊緣；文獻[8]和文獻[9]算法分割后圖像的邊緣完整度低. 對于Cameraman圖像，文獻[6]、文獻[7]和文獻[9]算法都存在欠分割現象，文獻[8]算法分割后圖像含有少量噪聲.

(a)原始圖像 (b)文獻[6] (c)文獻[7]

(d)文獻[8] (e)文獻[9] (f)本文算法圖3 Cameraman圖像分割效果Fig.3 Cameraman image segmentation results

為了對圖像分割效果進行定量評價，本文采用區域一致性(UM)、區域對比度(CM)、形狀測度(SM)[14]作為評價指標，對其進行客觀評價.

(1)區域一致性

(20)

(2)區域對比度

(21)

式中：uo為目標區域平均灰度級；ub為背景區域平均灰度級.

(3)形狀測度

▽(x,y)[sgn[f(x,y)-t]]

(22)

式中:fN(x,y)為鄰域N(x,y)的灰度均值;t為灰度閾值;▽(x,y)為廣義梯度;D為歸一化因子;sgn(x)為符號函數.

UM、CM、SM值越大，表明算法的可行性越高，圖像的分割效果越好，評價指標的實驗結果數據見表1，不同算法的UM、CM、SM對比曲線圖如圖4所示.

表1 不同算法的圖像分割效果評價

Tab.1 Image segmentation evaluation of different algorithms

圖像分割方法區域一致性(UM)區域對比度(CM)形狀測度(SM)Lena文獻[6]0.973 60.307 80.405 3文獻[7]0.984 20.485 10.389 1文獻[8]0.996 30.356 20.438 5文獻[9]0.997 60.491 70.419 7本文算法0.998 70.520 30.457 3Cameraman文獻[6]0.967 30.439 60.423 1文獻[7]0.972 60.537 10.497 6文獻[8]0.992 50.485 20.592 1文獻[9]0.984 70.583 20.578 3本文算法0.994 00.632 00.624 9

(a)Lena圖像

(b)Cameraman圖像圖4 不同算法的UM、CM、SM對比曲線圖Fig.4 UM、CM and SM contrast curves of different algorithms

由表1、圖4可以看出，本文算法分割圖像的區域一致性(UM)、區域對比度(CM)、形狀測度(SM)的值都高于各參考文獻算法，說明本算法的圖像分割效果更優.

運行處理時間也是評價圖像分割效果的重要指標. 本文算法和文獻[6]～文獻[9]算法的運行處理時間對比結果見表2.

表2 不同算法的圖像分割運行時間對比

Tab.2 Running time comparison of different algorithms for image segmentation s

圖像文獻[6]文獻[7]文獻[8]文獻[9]本文算法Lena0.835 70.683 40.702 10.627 30.496 0Cameraman0.765 30.638 10.491 30.574 20.456 9

由表2可以看出，本文算法相比各參考文獻算法，運行時間更少，效率更高.

4 結束語

本文提出的基于最小Tsallis交叉熵改進型PCNN圖像分割算法，在現有的簡化PCNN模型基礎上進行改進，引入抑制輸入項對內部活動項進行改進，優化閾值衰減函數.該算法能夠根據圖像特性自適應設置鏈接強度系數和鏈接權值矩陣. 引入最小交叉熵準則作為改進型PCNN的迭代終止判斷準則，可以有效加快迭代進程，引入雙邊濾波可以進一步完善圖像分割效果.仿真實驗結果表明，分割后圖像的區域一致性(UM)、區域對比度(CM)、形狀測度(SM)的值都有相應的提高，算法運行耗時更少，分割后圖像具有更好的魯棒性.