永磁同步電動機轉矩脈動抑制方法

程松遼， 陸永耕， 江澤昌， 袁紅杰， 賈竹青

(上海電機學院 電氣學院， 上海 201306)

永磁同步電動機(Permanent Magnet Synchronous Motor，PMSM)因其具有輸出功率高并且工作性能良好的優點，現已在各行各業得到廣泛應用[1]。直接轉矩控制(Direct Torque Control, DTC)理論提出得較晚，它相比于矢量控制有一些明顯的優勢。DTC坐標變換簡單，可以對轉矩進行直接控制，具有易于實施，系統響應速度快等優點。但傳統的DTC也存在一些缺點，如轉矩脈動大，耗損增加等[2]。

為了改善系統的缺陷，文獻[3-4]把零矢量引入到傳統的DTC中。運用Matlab軟件進行了仿真分析。仿真結果表明，在PMSM低速運行時零矢量對轉矩幾乎沒有影響,轉矩幾乎不變,但是當PMSM工作在較高的速度時,零矢量會優化輸出轉矩。

滑模控制(Sliding Mode Control，SMC)實質是一種非線性的控制方法[5-9]。滑動模態因為其本身的特征，能夠使SMC的響應速度快并且具有抗外界的擾動性強等優點[10]。同時SMC也存在抖振的問題，這使它在電力方面的應用受到了限制。但是高階的SMC可以使滑模集S能夠在有限的時間內收斂, 從而在一定程度上有效消除傳統SMC抖振的問題[11]，使得這種高階的SMC的控制性能良好。

文獻[12-14]二階滑模控制主要應用在磁鏈觀測器和控制器上。文獻[15]在基于空間矢量調制的直接轉矩控制中引入了二階滑模控制器，用它將其中僅有的兩個PI控制器進行了替換，使系統響應時間變短并且減小了轉矩脈動。

本文將零矢量引入到含有滯環比較器的傳統控制框圖中來減少轉矩脈動。為了更進一步優化控制系統，減小轉矩脈動以及提高速度的響應特性，先用雙曲正切函數h(s)代替符號函數sgn(s)對二階滑模控制器進行改進，然后再用其替換滯環控制框圖中僅有的PI控制器。

1 PMSM直接轉矩控制的基本理論

PMSM在α-β靜止坐標系下的電壓方程為

(1)

式中：Rs為定子電阻，Ω；uα，uβ為定子電壓在α和β軸的分量，V；iα，iβ為定子電流在α和β軸的分量，A；ψα，ψβ為定子磁鏈在α和β軸的分量，Wb。

磁鏈方程為

(2)

式中：Ls為隱極式PMSM電感，mH；ψf為永磁體磁鏈,Wb；θe為轉子位置角，(°)。

電磁轉矩方程為

(3)

式中：Te為電磁轉矩，N·m；pn為電動機的極對數。

運動方程為

Te-TL-Bωr=Jdωr/dt

(4)

式中：TL為負載轉矩，N·m；ωr為轉子速度,rad/s；B為摩擦系數；J為轉動慣量,kg·m2。

PMSM在d-q坐標系下的電壓方程為

(5)

式中：ud，uq分別為定子電壓在d和q軸上的分量，V；id，iq分別為定子電流在d和q軸上的分量，A；ψd，ψq為定子磁鏈在d和q軸上的分量，Wb。

磁鏈方程為

(6)

式中：Ld，Lq分別為電感在d和q軸上的分量，mH。

隱極式PMSM滿足

Ld=Lq=Ls

(7)

電磁轉矩方程為

(8)

2 含零矢量DTC

2.1 含零矢量DTC原理

當引入零矢量時，轉矩的變量為

(9)

式中：Ts為控制周期，μs；ψs為定子磁鏈，Wb；δ為轉矩角，(°)。

從式(9)可知，在引入零矢量后，轉矩減小。當PMSM的ωr很小時，因為系統的控制周期只有幾十μs，所以ωrTs就趨近于0，那么ΔTe也幾乎為0，零矢量不會對轉矩的輸出產生影響。PMSM的ωr明顯變大時，ωrTs就比較大，所以看出ΔTe<0，零矢量在這里使轉矩的效果變好。隨著PMSM的ωr變大，零矢量優化輸出Te的效果就越顯著。

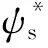
圖1 磁鏈雙層滯環結構圖

圖2 轉矩雙層滯環結構圖

結合圖1和圖2，確定各個扇區不同情況下的開關矢量作用順序，得到空間電壓矢量圖(見圖3)和含零矢量DTC開關表(見表1)。θ1～θ6分別為圖3中6個扇區編號。

2.2 對比仿真

為了驗證將零矢量引入到DTC能起到優化控制系統，提高系統的控制性能，本文運用Matlab軟件進行了仿真。將零矢量DTC和傳統DTC進行對比。在仿真中使用的參數如表2所示。PMSM的額定轉速設為600 r/min,起始負載轉矩為0 N·m，0.2 s時負載從0 N·m突變為1.5 N·m。仿真條件設置為：直流側電壓UDC=311 V，采用變步長ode23tb算法，仿真時間為0.4 s。

圖3 空間電壓矢量圖

ψτθ1θ2θ3θ4θ5θ611u6u2u3u1u5u40u7u0u7u0u7u0-1u7u0u7u0u7u0-2u5u4u6u2u3u101u2u3u1u5u4u60u0u7u0u7u0u7-1u0u7u0u7u0u7-2u1u5u4u6u2u321u6u2u3u1u5u40u4u6u2u3u1u5-1u4u6u2u3u1u5-2u5u4u6u2u3u1

表2 PMSM參數

傳統PI控制器的轉速、轉矩波形如圖4所示。基于零矢量的轉速、轉矩波形如圖5所示。圖4和圖5中的小圖均為其局部放大圖。由圖4(a)和圖5(a)可見，含有零矢量的PMSM的DTC比傳統的PMSM的DTC的動態響應速度快。由圖4、圖5還可見，傳統的DTC的轉速波形超調大，動態響應時間慢，在約0.10 s才穩定到給定值，而含有零矢量的DTC的轉速波形超調變小，同時響應速度快，在0.06 s就穩定到了給定值。使用零矢量的DTC和傳統的DTC相比，轉矩輸出效果明顯變好，二者的轉矩響應如圖4(b)和圖5(b)所示。從仿真波形可以看出傳統的DTC的轉矩波形在系統穩定之后波動范圍為1.30～1.72 N·m，轉矩脈動為0.42 N·m；而使用零矢量的DTC的轉矩在穩定狀態下的波動范圍為1.37～1.64 N·m，轉矩脈動為0.27 N·m，其轉矩脈動明顯小于傳統DTC的轉矩脈動。轉矩脈動越小，表明控制性能越良好。

(a) 轉速響應波形

(b) 轉矩響應波形

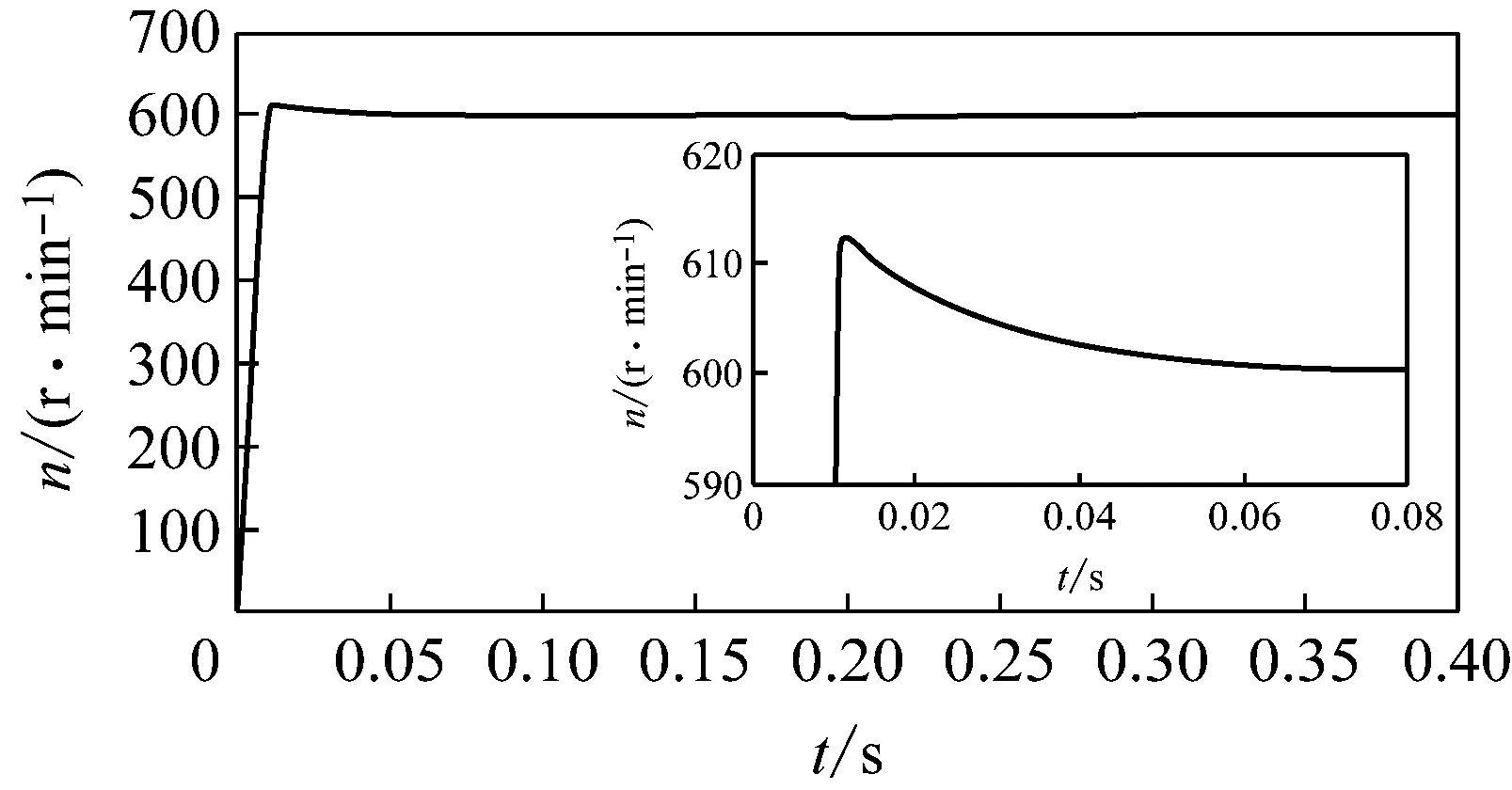
(a) 轉速響應波形

(b) 轉矩響應波形

3 二階滑模控制器設計

為進一步減小含有零矢量的DTC的轉矩脈動，本文設計一種二階滑模控制器代替PI控制器，同時用雙曲正切函數h(s)代替符號函數sgn(s)，增強了系統的魯棒性。

3.1 Super-twisting 控制原理

對于所有單輸入非線性系統

(10)

式中：x為狀態變量，x∈Rn；u為控制系統的輸入變量，u∈R；y為控制系統的輸出；σ(t,x)為輸出函數，稱為滑模變量；a(t,x)，b(t,x)為連續的未知函數。

控制目的是讓系統能夠在短時間內到達滑模面σ(t,x)=0。對σ(t,x)進行二階求導，可得

(11)

f(t,x)和g(t,x)為不確定函數， 存在正數C,Km,KM,使得?u，?x，有

(12)

設式(12)在所有的范圍內都滿足，則

(13)

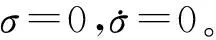
因此，問題變為尋找一個反饋

(14)

Super-twisting算法的控制律設計如下式所示：

(15)

式中：KP和KI為正增益，取值范圍由

(16)

決定。

若式(10)的條件滿足式(12)，與此同時式(15)滿足式(16)條件，能夠使Super-twisting滑模(Super-twisting Slidng Mode, STSM)控制結構在較短的時間收斂。

3.2 Super-twisting控制器設計

PMSM轉子動力學方程為

(17)

假設ψs恒定，由式(17)可推導出轉速的二階導數為

(18)

式(18)中轉速、轉動慣量和負載轉矩都是有界的，因此式(18)滿足式(12)。Super-twisting轉速控制器可設計為

(19)

(20)

式中：sω為轉速誤差，sω=ω*-ω；KP，KI為正增益，滿足式(16)的條件。

為了使控制性能更好，將符號函數sgn(s)用雙曲正切函數h(s)代替，即

(21)

式中：a為可調參數，調整a的值，可以改變雙曲正切函數在原點處的斜率。

優化后的Super-twisting轉速控制器為

(22)

根據式(22)設計的Super-twisting轉速控制器如圖6所示。

圖6 Super-twisting轉速控制器

將STSM轉速控制器應用于基于零矢量的PMSM的DTC中去得到控制框圖(見圖7)。

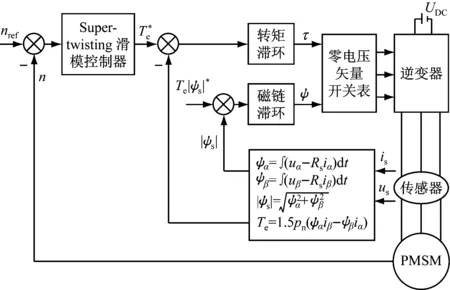
圖7 基于STSM轉速控制器的含零矢量DTC框圖

4 仿真及結果分析

在這里使用上文設置的PMSM參數。起始負載轉矩為0 N·m，0.2 s時負載從0 N·m突變為1.5 N·m。仿真時間為0.4 s。根據Matlab/Simulink軟件的仿真結果，分析了基于STSM轉速控制器的零矢量DTC的電磁轉矩波形和轉速波形(見圖8)，并與僅含有零矢量的DTC仿真波形(見圖5)進行對比。圖8中的小圖為其局部放大圖。

從圖5(a)和圖8(a)可知，基于STSM的零矢量DTC比基于零矢量的PMSM的DTC的動態響應速度快。基于零矢量的DTC的轉速波形超調略大，動態響應時間略慢，在約60 ms才穩定到給定值。而含有STSM轉速控制器的DTC的轉速波形超調明顯減小，且動態響應時間極快。在約5 ms就穩定到了給定值。使用了STSM轉速控制器的DTC和只使用零矢量的DTC相比有著更小的轉矩脈動，二者的轉矩響應波形如圖5(b)和圖8(b)所示。從仿真的波形可以看出，基于零矢量的PMSM的DTC在系統穩定之后波動的范圍為1.37～1.64 N·m，轉矩脈動為0.27 N·m,而使用STSM轉速控制器的零矢量DTC的轉矩在穩定狀態下的波動范圍為1.4～1.6 N·m，轉矩脈動為0.2 N·m。

(a) 轉速響應波形

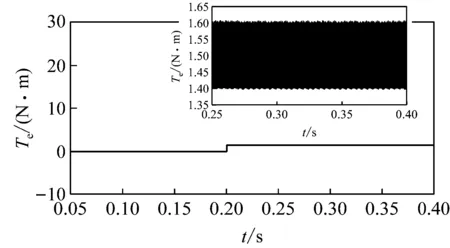
(b) 轉矩響應波形

5 結 語

本文設計了一種基于STSM轉速控制器的PMSM含零矢量DTC。通過合理的使用零矢量，基于零矢量的DTC相比于傳統的DTC，轉矩脈動抑制效果顯著提升，與此同時轉速的超調變小并且其響應速度變快。PMSM是一個非線性的系統，在系統運行時，傳統的PID在遇到很多情況時，控制效果并不理想。為了讓系統運行效果更好，將改進后的STSM轉速控制器用于含零矢量DTC當中。由仿真可知，這種含有STSM轉速控制器的零矢量DTC，使系統超調更小，響應時間短，進一步減小了轉矩脈動，提高了系統的控制性能。