結(jié)合八叉樹結(jié)構(gòu)對ICP算法在點云配準方面的改進

呂明慧

（山東科技大學 山東 青島 266590）

1 引言

隨著三維激光掃描技術(shù)的廣泛應用，三維激光掃描儀和它所獲取的點云數(shù)據(jù)的處理方法也在飛速發(fā)展。近些年來，三維激光掃描儀的技術(shù)已經(jīng)初步成熟，獲取被測地物的點云數(shù)據(jù)的精度和密度都達到了現(xiàn)階段社會發(fā)展的要求，但大量的點云數(shù)據(jù)處理是我們面臨的一大難題。點云數(shù)據(jù)處理的難度主要體現(xiàn)在點云數(shù)據(jù)的拼接與配準方面，本文則主要介紹一種在原有ICP算法的基礎(chǔ)上，結(jié)合八叉樹結(jié)構(gòu)的點云配準方法。

2 八叉樹

2.1 八叉樹結(jié)構(gòu)

八叉樹結(jié)構(gòu)是由四叉樹結(jié)構(gòu)推廣到三維空間而形成的一種三維數(shù)據(jù)結(jié)構(gòu)。主要思想就是將一個空間三維模型用一個正方體進行包圍，按照三維直角坐標的方式進行八等份切割，將每一個切割所得到的結(jié)構(gòu)體存儲在其下屬的小區(qū)域內(nèi)，對于每個區(qū)域都用相同的方式再向下分割，直到子區(qū)域內(nèi)為空或達到某一規(guī)定條件。圖1為八叉樹結(jié)構(gòu)示意圖。

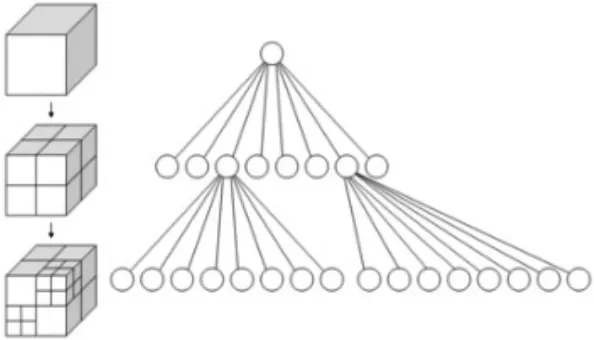
圖1

在應用八叉樹結(jié)構(gòu)進行數(shù)據(jù)組織時，通常利用Morton碼作為一種較好的編碼方式，還可以應用改進后的Morton碼[1]，一種線性八叉樹地址碼進行編碼。

2.2 八叉樹應用于點云配準

通常的點云配準方式為利用ICP算法進行配準，但ICP算法在有一個較好的初值時能得到比較理想的配準結(jié)果，否則此算法會含有較大的誤差。而八叉樹結(jié)構(gòu)則可以較好的解決這個問題。基本思路為在兩個點集中分別以八叉樹結(jié)構(gòu)組織數(shù)據(jù)，則每一個根節(jié)點或是葉節(jié)點都有其相應的屬性信息，包括坐標數(shù)據(jù)和體積數(shù)據(jù)。我們的目標就是找出兩個點集中最為密合的部分，即在空間位置上相差最小甚至是完全相同的兩個點，那么就可以利用八叉樹結(jié)構(gòu)快速而精確地找到這兩個點。

具體方法為自頂向下分別對兩個點集的同層根節(jié)點進行比較，比較每個相對應的根節(jié)點，根據(jù)根節(jié)點內(nèi)的坐標信息求取其對應的重心坐標，以兩個完全平方和相差最小的重心坐標所在的根節(jié)點為目標點進行下一層根節(jié)點的比較，用同樣的方法求取重心坐標進行比較，以此類推，依次向下總能求取出兩個相對應的點或點集。用這種方法求解時，為了避免不必要的時間和精度浪費可以設(shè)置兩個重心點的相對精度初步得到兩個點集，后續(xù)的精度提高可以再利用迭代進行調(diào)整。這種得到最鄰近點或點集的方式不僅可以提高精度，還能夠減少處理時間，相比于以往的遍歷每個點的方式所提高的處理速度是指數(shù)級的。

3 應用八叉樹結(jié)構(gòu)對ICP算法的改進

3.1 ICP算法

經(jīng)典的ICP算法的基本原理很簡單，就是要求兩個點云數(shù)據(jù)之間的變換關(guān)系，實質(zhì)上的不同的坐標系統(tǒng)轉(zhuǎn)換到相同坐標系統(tǒng)下的計算。坐標系統(tǒng)的轉(zhuǎn)換一般是利用七參數(shù)法，三個平移參數(shù)，三個旋轉(zhuǎn)參數(shù)和一個比例縮放因子。而在點云數(shù)據(jù)中，我們默認比例縮放因子為1，即將問題轉(zhuǎn)化為求解一個旋轉(zhuǎn)矩陣和一個平移向量。它們的解算方法即為ICP迭代最近點算法[2-3]。有很多對于此種算法的改進方法，大多是利用去除誤差較大的點對或是給不同的約束條件分配權(quán)重來減小誤差，對于ICP算法來說，耗費時間最長的部分就是對應點的計算，接下來將介紹在八叉樹結(jié)構(gòu)的參與下，以迭代方式不斷地改進點集的重心坐標來快速精確定位兩個空間位置最鄰近點甚至是重合點。

3.2 應用八叉樹結(jié)構(gòu)的ICP算法

基于ICP算法的基本原理[4]，有以下的解算步驟：（1）根據(jù)參考點集中的點坐標，在待配準點集上搜索相應最近點點集；（2）計算兩個點集的重心位置坐標，并進行點集中心化生成新的點集；（3）由新的點集計算正定矩陣N，并計算N的最大特征值及其最大特征向量；（4）由于最大特征向量等價于殘差平方和最小時的旋轉(zhuǎn)四元數(shù)，將四元數(shù)轉(zhuǎn)換為旋轉(zhuǎn)矩陣R；（5）在旋轉(zhuǎn)矩陣R被確定后，由平移向量t僅僅是兩個點集的重心差異，可以通過兩個坐標系中的重心點和旋轉(zhuǎn)矩陣確定；（6）由參考點集計算旋轉(zhuǎn)連續(xù)兩次距離平方和之差絕對值作為迭代判斷數(shù)值；（7）當此數(shù)值滿足一定精度要求時，ICP配準算法就停止迭代，否則重復（1）至（6）步，直到滿足條件后停止迭代。

八叉樹結(jié)構(gòu)可以應用于一、二兩個解算步驟，在搜索最近點點集時，不采用遍歷搜索，而是進行前文所說的八叉樹結(jié)構(gòu)搜索提高搜索速度。這個點集可以作為配準的最初點集來使用，有了最初的相對精度較高的起算數(shù)據(jù)，就可以得到比較好的配準結(jié)果了。由這個點集繼續(xù)進行ICP算法的后續(xù)計算直到計算出第一個旋轉(zhuǎn)矩陣和平移參數(shù)。由于有很多次的迭代，每次迭代都是用八叉樹結(jié)構(gòu)進行查找而不是遍歷每一個點進行歐氏距離的解算，因此它所提高的工作速度是巨大的。接下來進行迭代計算，下面的解算步驟也是八叉樹起到改進作用的主要部分。

由第一次計算的旋轉(zhuǎn)矩陣和平移參數(shù)解算出待配準點集在參考點集坐標系下的坐標值，計算出重心坐標，根據(jù)重心坐標取一定半徑的球內(nèi)的臨近點形成新的點集，對新的點集數(shù)據(jù)重新按照八叉樹結(jié)構(gòu)進行組織，再與參考點集進行同層次根節(jié)點的三維重心坐標差平方和的比較，找出最鄰近的兩個坐標點。這里找出的是兩個相對應的坐標點，而不是兩個點集，由于不斷地進行迭代，所查找的點集的重心位置也在不斷改變，因此靈活性有了很大的提升，避免了有更加匹配的點對而無法發(fā)現(xiàn)的情況的發(fā)生。經(jīng)過一定次數(shù)的迭代，利用八叉樹結(jié)構(gòu)總是能查找到一對最為臨近甚至是空間位置相同的對應點，此時的迭代條件可以是兩對應點對的相對精度。這樣就完成了一個點對的查找。根據(jù)實際掃描情況，一定是有多個配準特征可供選擇，那么只要在兩個點云數(shù)據(jù)中完成上述三個對應點對的查找就可以解算出不同坐標系的轉(zhuǎn)換參數(shù)，即完成點云數(shù)據(jù)的配準工作。若是對更多的點集進行比較計算，則可以求解出很多相應的點對，選擇其中誤差最小的幾對數(shù)據(jù)進行解算即可進一步提高配準精度。

4 結(jié)語

這種結(jié)合八叉樹的點云配準算法與經(jīng)典ICP算法的本質(zhì)上的不同在于它是根據(jù)解算查找出的對應點對來精確計算最終的旋轉(zhuǎn)矩陣和平移參數(shù)，而不是直接用點集進行解算。它的優(yōu)勢體現(xiàn)在兩個方面，一是在每一次迭代計算中都提高了運算速度，二是由重心位置不斷改變的空間球狀點集利用八叉樹結(jié)構(gòu)一步步找出最鄰近點對，提高了配準精度。八叉樹結(jié)構(gòu)特殊的數(shù)據(jù)組織方式和查找方式是提高點云配準速度和精度的關(guān)鍵。