鄂爾多斯市潛在蒸散發時空變化分析

徐麗娟 張文鴿 李皓冰 譚力

摘要：依據Priestley-Taylor潛在蒸散發量計算模型，AmODIS、GLDAS等多源遙感數據基礎上，對鄂爾多斯市2001-2012年的地表潛在蒸散發進行了模擬。結果表明：基于多源遙感數據的Priestley-Taylor模型對鄂爾多斯市潛在蒸散發的模擬效果較好；從時間序列上看，鄂爾多斯市2001-2012年潛在蒸散發量總體呈增長趨勢，增長率為8.26mm/a；7月潛在蒸散發量為170.44mm，為全年最大值，5-8月潛在蒸散發量占全年的55.56%；從空間分布上看，鄂爾多斯市潛在蒸散發主要發生在草地、沙漠和耕地，三者的潛在蒸散發量分別占總量的50.62%、34.58%、14.35%。

關鍵詞：Priestley-Taylor模型；時空變化；潛在蒸散發；鄂爾多斯市；2001-2012年

中圖分類號：P426.2 文獻標志碼：A Doi：10.3969/j.issn.1000-1379.2018.09.013

受氣候變化和人類活動的影響，鄂爾多斯市水文循環發生了顯著變化。潛在蒸散發可反映區域的蒸發能力，是地表能量平衡、水文循環的重要環節。對潛在蒸散發進行大空間尺度計算以及相關分析，對于研究當地的氣象干旱、氣候變化等有重要意義[1]。

近年來，對于潛在蒸散發的研究越來越受到重視和關注。國內外對于潛在蒸散發的研究已取得較多成果，如：張洪波等[2]以徑河流域為研究對象，采用SWAT模型模擬該流域的潛在蒸發量；曹永強等[3]采用Penman-Monteith法，估算了遼寧省1965-2014年的潛在蒸散發量，結果表明近50a來遼寧省潛在蒸散發量呈顯著減小趨勢，在空間上由西向東遞減；趙捷等[4]利用黑河流域15個氣象站點41a的逐日觀測資料，應用Penman-Monteith模型，結合Spline插值方法，分析了黑河流域潛在蒸散發的時空變化，結果表明多數站點的潛在蒸散發量呈下降趨勢；王亞敏等[5]利用FAO Penman-Monteith模型計算出潛在蒸發量，采用數理統計理論和GIS空間分析技術，對河西地區潛在蒸發量的時空特征進行了分析，結果表明河西地區潛在蒸發量總體呈波動下降趨勢；Hember R.A.等[6]采用Priestley-Taylor模型估算了北美森林地區從1951年至2014年的潛在蒸發量，預計該地區未來潛在蒸發量呈上升趨勢；Sauda.等[7]通過研究Thornth-waite、Blaney-Criddle、Kharufa和Ivanov等人的方法，分析了伊拉克西部山谷潛在蒸散發的時空變化。

本文在構建MODIS、GLDAS、DEM多源遙感數據庫的基礎上，基于Priesdey-Taylor潛在蒸散發量計算模型，對鄂爾多斯市2001-2012年的潛在蒸散發量進行計算，并對計算結果進行時空變化分析。

1 基于多源數據的Priestley-Taylor潛在蒸散發量計算模型

1.1 Priestley-Taylor潛在蒸散發量計算模型

Priestley-Taylor模型[8]是在地表能量平衡過程基礎上引入系數，從而推導無平流條件下潛在蒸散發的模型。跟彭曼模型[9]相比Priestley-Taylor模型輸入參數更少，且不需要空氣動力等參數。Priestley-Taylor模型的計算公式為式中：ETp為潛在蒸散發量，mm；α為Priestley-Taylor模型系數；Rn為地表凈輻射量，W/m2；G為土壤熱通量，W/m2；λ為汽化潛熱，MJ/kg，取2.45；Δ為飽和水汽壓—溫度曲線的斜率，kPa/℃；γ為干濕表常數，kPa/℃。

本文取MODIS衛星過境時刻的地表凈輻射量為計算點，表達式為

Rn=（1-α）Rs+R1↓-R1↑（2）式中：Rs為太陽短波輻射能量W/m2 ；R1↓為地表吸收的大氣長波輻射能量；R1↑ 為地表發射的長波輻射能量。

Rs的計算公式為

τ=0.75+2×10-5H（4）

θz=cos（sinφsinδ+cosφcosδcosω）（5）式中：I0為太陽常數；τ為大氣透射率；θz為太陽天頂角，rad；R為日地距離訂正因子；H為海拔，m，由DEM獲得；φ為地理緯度，rad；δ為太陽赤度，rad；ω為太陽時角，rad。

δ、ω的表達式分別為式中：ψ為太陽日角rad ；DOY為計算日期在當年內天數的排序；t為計算的時刻；lm為計算點的經度，rad；lz為當地時區中心經度，rad；Sc為太陽時的季節矯正。

太陽赤度和太陽時的季節矯正由下式估算[10]：f（ψ）=0.0069-0.4cosψ+0.07sinψ-0.0068cos 2ψ+0.0009sin 2ψ-0.0027cos 3ψ+0.0015 sin 3ψ（8）

R1↓-R↑可表示為

R1↓-R↑=δεaεsTa4-δεsTs4（10）

εa=9.2×10-6Ta2（11）

εs=0.273+1.778ε31-1.807ε31ε32-

1.037ε32+1.774ε322（12）式中：δ為常數，取值為5.67×10-8W/（m2·K4）；εa為大氣發射率；εs為地表發射率；Ta為氣溫，℃；Ts為地表溫度，℃；ε31、ε32分別為MODIS第31、32波段的發射率[11]。

土壤熱通量不能用遙感衛星進行檢測，可以通過植被覆蓋度與地表凈輻射之間的關系進行度量：

G=Rn[Гc+（1-fc）（Гa-Гc）]（13）

fc=（NDVI-NDVlsoil）/（NDVIveg-NDVIsoil）

（14）式中：fc為植被覆蓋度；Гs為全部裸地情況下土壤熱通量與地表凈輻射量的比值，取0.315；Гc為植被完全覆蓋區土壤熱通量與地表凈輻射量的比值，取0.05；NDVI為歸一化植被指數；NDVIsoil為裸土區的歸一化植被指數[12]； NDVIveg為植被覆蓋區的歸一化植被指數。

干濕表常數γ的計算式為式中：Cp為空氣定壓比熱，MJ·kg/℃，取值為1.013×10-3；Pr為大氣壓，kPa/℃；ε為水汽化學式量與干空氣化學式量之比。

飽和水汽壓—溫度曲線斜率△可表示為式中：trise為日出時間；tset為日落時間；t為計算潛在蒸散發量對應的時間；ETp_max為一天內最大潛在蒸散發量，mm。

1.2 MODIS、GLDAS、DEM多源數據

針對研究區域氣象資料獲取不全面的情況，本文采用MODIS、GLDAS、DEM多源數據作為模型基礎參數。

（1）MODIS數據。MOD11Al是1d合成的空間分辨率為1000m的地表溫度和地表發射率產品。MOD13A2是16d合成的空間分辨率為1000m的植被指數產品，包括植被指數（NDVI）和增強性植被指數（EVI），本文采用植被指數NDVI。MCD43B3為8d時間分辨率、1000m空間分辨率數據，提供地表反照率數據。

（2）GLDAS氣溫數據及預處理。在計算地表吸收的長波輻射時，需要大氣溫度數據，本研究采用GLDAS提供的0.25°×0.25°空間分辨率、3h時間分辨率的遙感數據。本研究空間分辨率統一為0.01°×0.01°，因此需要對大氣溫度的0.25°×0.25°數據進行降尺度處理。

由于大氣溫度降尺度插值處理精度跟當地的海拔高度等因素相關，因此在插值處理前要先對大氣溫度進行基于海拔的還原操作，即將大氣溫度還原到海平面對應的大氣溫度，然后再進行線性插值操作，得到對應的0.01°×0.01°大氣溫度數據，最后根據逆運算得到正常海拔高度下的氣溫數據。計算公式為

Tair'=Tair+mH（19）式中：Tair'為對應的海平面大氣溫度數據；Tair為原始大氣溫度數據；m為濕絕熱直減率，取0.6℃/100m。

（3）DEM地面高程數據。DEM數字高程采用地理空間數據云提供的90m分辨率數據。在ENVI平臺中對其進行重采樣操作，獲得0.01°×0.01°空間分辨率、WGS-84坐標系格式的DEM數據。

2 實例應用

2.1 研究區概況

鄂爾多斯市位于內蒙古自治區西南部，地處鄂爾多斯高原腹地，與呼和浩特市、烏海市、阿拉善盟、包頭市等接壤，屬典型的溫帶大陸性氣候區，日照豐富，四季分明，無霜期短，干旱少雨，蒸發量大。年日照時數為2716.4～3193.9h，境內不同地區年均氣溫為5.3～8.7℃，全年氣溫日較差為11～15℃，年較差為45～50℃。東部地區年降水量為300～400mm，西部地區為190～350mm，全年降水集中在7-9月。蒸發量大，年蒸發能力為2000～3000mm。鄂爾多斯市行政區劃見圖1。

2.2 鄂爾多斯市ETp計算結果

在構建多源遙感來源數據庫和基于Priestley-Taylor模型計算潛在蒸散發量的基礎上，對鄂爾多斯市2001-2012年逐日潛在蒸散發量進行模擬并進行累加，得到逐年潛在蒸散發影像（見圖2）。

在沒有實測資料的情況下，由于水面蒸發量是對應區域充分灌水條件下的蒸發量，反映了當地的蒸發能力，與潛在蒸散發有良好的相關性，因此本文采用ETp與水面蒸發量之間的相關性對ETp的計算結果進行精度驗證。選取杭錦旗建設灌域吉日嘎郎圖鎮試驗場蒸發皿監測數據進行分析，該試驗場使用20cm口徑蒸發皿進行逐日水面蒸發監測，驗證資料選取2006年3月至2008年10月的月蒸發量數據。20cm口徑蒸發皿與E601蒸發皿的折算系數采用鄂爾多斯市東勝氣象站（國家基準站）2000-2001年蒸發試驗得到的結果[13]，取0.47。對于E601與真實水域的折算系數，俄羅斯和美國的相關學者研究認為其值為0.90～0.91，我國沒有公認的研究結果，故本次研究選取0.90。因此，本次研究最終的蒸發皿折算系數取0.423。模擬得到的ETp與水面蒸發量的相關關系見圖3，模擬值與實測值的相關系數為0.9048，說明潛在蒸散發的模擬精度令人滿意。

2.3 鄂爾多斯市ETp時間變化分析

從2001-2012年年均ETp的變化（見圖4）可知：2001-2012年鄂爾多斯市潛在蒸散發量總體呈增長趨勢，增長速率約為8.26mm/a；ET的最小值（1057.81～）出現在2001年，最大值（1210.23mm）出現在2012年。本次研究的結果與劉昌明等[川對黃河流域潛在蒸散發的研究結果相符，說明基于多源遙感數據的Priestley-Taylor模型對鄂爾多斯市潛在蒸散發模擬效果較好。

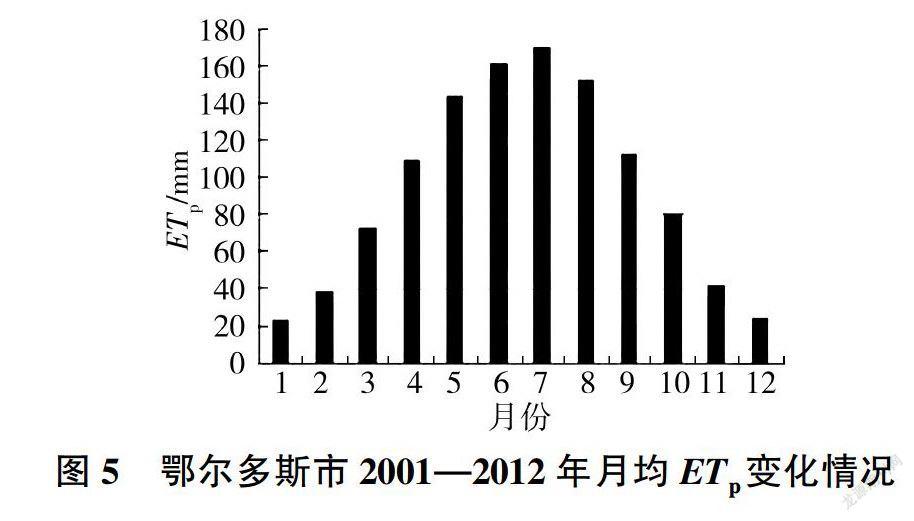
從月均潛在蒸散發變化情況（見圖5）可知：鄂爾多斯市潛在蒸散發量年內大致呈正態分布；1月太陽輻射強度小，地表凈輻射量低，潛在蒸散發量為22.95mm，是全年最小值；隨著時間推移，地面接收的太陽短波輻射逐漸增強，同時隨著植被指數增大，地表能量吸收率增大，地面凈輻射量也隨之增大，7月潛在蒸散發量達到全年最大的170.44mm；5-8月的潛在蒸散發量占全年的55.56%。

2.4 鄂爾多斯市ETp空間分布分析

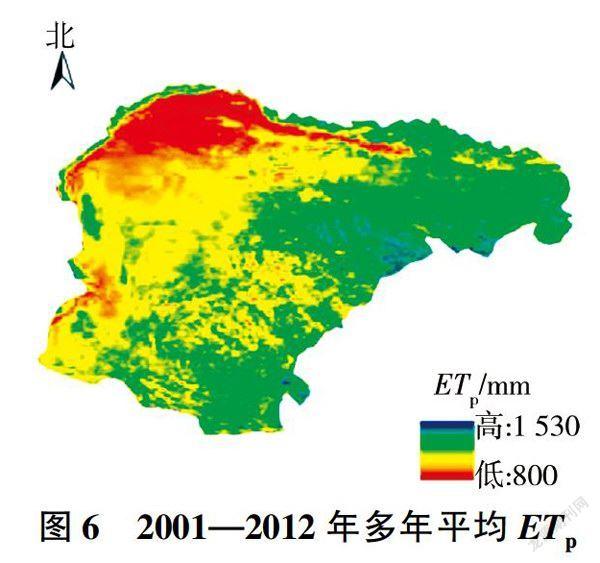
對2001-2012年多年平均ETp影像（見圖6）分析可知，鄂爾多斯市北部的庫布齊沙漠地表發射率和地表反射率都比較大并且降水量小，因此其地表凈輻射量較小，導致其處于整個研究區域潛在蒸散發量的低值區，多年平均潛在蒸散發量只有800mm。同時，鄂爾多斯高原西部屬于半荒漠草原地帶，地勢平坦，起伏不大，氣候比較干旱且降雨稀少，因此該區域也處于潛在蒸散發量的低值區。中部毛烏素沙地由于地下水蘊藏條件較好，地表發射的短波輻射相對較少，同時毛烏素沙地有零星草地分布，地表對太陽輻射的短波輻射吸收較多，故潛在蒸散發相對庫布齊沙漠大，為1000～1200mm，屬于中值區。北部沿黃灌區有較好的灌溉條件，地下水埋深較淺，地表凈輻射量較大，因此潛在蒸散發量較大。東部準格爾旗大部分地區溝壑縱橫，河流分布廣泛，加上草地覆蓋較廣，因此其處于潛在蒸散發量的高值區，最高達到1500mm，

盧娜等[15]在利用地面實測蒸發量對SEBS（Surface Energy Balance System，地表能量平衡系統）模型參數進行率定的基礎上，依據NOAA（NationalOceanic and Atmospheric Administration，美國國家海洋和大氣管理局）衛星資料，對鄂爾多斯市北部盆地蒸散量進行模擬，研究顯示鄂爾多斯市北部地區蒸發量高值為1 500mm左右，與本次研究的結果基本相符。

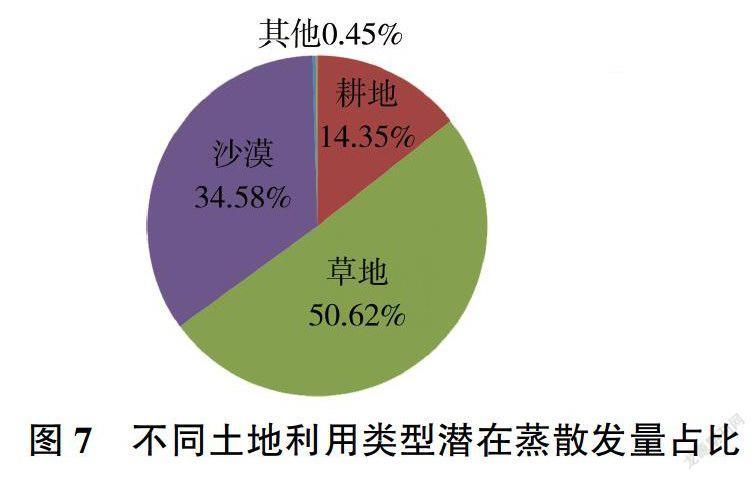
從鄂爾多斯市多年平均ETp的計算結果（見圖7）和鄂爾多斯市土地利用現狀可知，鄂爾多斯市草地、沙漠、耕地面積占比大，其潛在蒸散發量分別占總量的50.62%、34.58%、14.35%，其他土地利用類型占比過小，占總量的比例不超過1%。

3 結語

（1）鄂爾多斯市2001-2012年潛在蒸散發量為1057.81～1210.23mm，由北向南呈增大趨勢。

（2）鄂爾多斯市多年月均潛在蒸散發量大致呈正態分布。1月潛在蒸散發量為22.95mm，是全年最小值。7月潛在蒸散發量為170.44mm，為全年最大值。5-8月潛在蒸散發量占全年的55.56%。多年平均潛在蒸散發量西北地區較低，東南地區較高。

（3）傳統的潛在蒸散發計算方法依托氣象站點數據，只能代表某一個站點的潛在蒸散發，而基于遙感數據的潛在蒸散發模型實現了從點到面的跨越，展現了遙感數據在長系列時間和大空間尺度地物信息監測的優勢。本次研究基于MODIS、GLDAS等多源遙感數據庫，依據Priestley-Taylor計算模型對鄂爾多斯市2001-2012年逐日潛在蒸散發進行模擬，取得了較好的模擬效果。

參考文獻：

[1]穆少杰，李建龍，陳奕兆，等.2001-2010年內蒙古植被覆蓋度時空變化特征[J].地理學報，2012（9）：1255-1268.

[2]張洪波，顧磊，辛深，等.徑河流域干旱特征時空變化研究[J].華北水利水電大學學報（自然科學版）12016737（3）：1-10.

[3]曹永強，高璐，袁立婷，等.遼寧省潛在蒸散發量及其敏感性規律分析[J].地理科學，2017，37（9）：1422-1429.

[4]趙捷，徐宗學，左德鵬.黑河流域潛在蒸散發量時空變化特征分析[J].北京師范大學學報（自然科學版），2013，49（增刊1）：164-169.

[5]王亞敏，張勃，戴聲佩，等.河西地區1960年至2008年潛在蒸發量的時空變化分析[J].資源科學，2010，32（1）：139-148.

[6]HEMBER R A，COOPS N C，SPITTLEHOUSE D L.Spatialand Temporal Variability of Potential Evaporation AcrossNorth American Forests[J].Hydrology，2017，4（1）：5-29.

[7]SAUD A，AZLINm，SAIDm，et al.Temporal and SpatialVariability of Potential Evapotranspiration in Semi-Arid Re-gion：Case Study the Valleys of Western Region of Iraq[J].International Journal of Engineering Science&Technology，2014，6（9）：653-660.

[8]劉紹民，劉志輝.用Priestley-Taylor公式估算作物農田蒸散量的研究[J].高原氣象，1997（2）：80-85.

[9]劉懷屺.蒸發力計算方法——彭曼（H.L.Penman）公式的應用[J].山東農業科學，1989（6）：22-24.

[10]左大康，周允華，項月琴，等.地球表層輻射研究[M].北京：科學出版社，1991：34-37.

[11]宋富強，邢開雄，劉陽，等.基于MODIS/NDVI的陜北地區植被動態監測與評價[J].生態學報，2011（2）：354-363.

[12]楊靜學，黃本勝，陳亮雄，等.基于PT-T和SBDART模型的按樹人工林蒸散量研究[J].華南師范大學學報（自然科學版），2014，46（4）：103-109.

[13]葉劍鋒，伶延輝，白連軍，等.20cm口徑蒸發皿代表性和折算系數的計算分析[J].水利科技與經濟，2009（11）：996-997.

[14]劉昌明，張丹中國地表潛在蒸散發敏感性的時空變化特征分析[J].地理學報，2011（5）：579-588.

[15]盧娜，萬力.基于RS的鄂爾多斯北部盆地地表蒸發量的計算[J].地質通報，2008（8）：1165-1167.