上埋式涵洞豎向土壓力計算的新方法

劉凱 向先超 范志強 宋伯石

摘 要：為求得符合實際情況的上埋式涵洞涵預面豎向土壓力及涵頂填土內豎向土壓力分布的變化規律，基于馬斯頓理論，改進其分析模型，提出了新的計算方法。利用FLAC3D建立涵洞的數值分析模型，分析公式推導中的部分參數，推導出最終的計算公式。通過數值模擬、公式計算和與前人研究的成果對比可得出：上埋式涵洞涵頂面以及距離涵頂面不同高度處的層面上，其豎向土壓力呈現中間大兩側小、土壓力集中的曲線分布，且填土高度越高、越靠近涵頂面的豎向土壓力集中效應就越明顯，涵頂點與兩側豎向土壓力差值也越大。推導出的計算公式能較為準確地計算出涵頂土體中各點的豎向土壓力大小，并體現出豎向土壓力分布隨著距離涵頂面高度變化的規律。

關鍵詞：涵洞：土壓力計算；FLAC3D；豎向土壓力；馬斯頓理論

中圖分類號：TV222.2；U449

文獻標志碼：A

doi： 10.3969/j.issn.1000-1379.2018.06.024

涵洞是指修筑于地面之下用于輸油氣水或供交通使用的建筑物，在公路、鐵路、水利、市政等工程中廣泛應用。根據埋設方式不同，涵洞可分為溝埋式、上埋式和隧洞式3種形式。不同埋設方式的涵洞，由于受力特征各不相同，因此涵頂填土壓力的計算方法存在差別。在此，筆者著重研究上埋式涵洞涵頂填土的受力特點，并對其豎向土壓力的計算方法進行研究。

以往上埋式涵洞土壓力計算方法中應用較廣的是散體極限平衡法，該方法的主要依據是Marston理論[1]，即假設上埋式涵洞中填土在自重壓力下發生沉降，但在沉降過程中，由于涵洞的剛度大于填土的剛度，涵洞上部的土體（內土柱）沉降小于涵洞外側的土體（外土柱），因此內外土柱之間會存在一個剪切面，外土柱沿剪切面給予內土柱一個向下的剪切力，于是涵洞受到的土壓力是內土柱白重與外土柱對其剪切力之和。Marston理論可謂奠定了埋地涵洞土壓力計算的基礎，其后諸多學者在此基礎上分別結合自己的見解和假設，提出過一些上埋式涵洞土壓力計算模型。如：曾國熙[2]認為內外土柱之間的側向作用力應為根據朗肯土壓力得出的水平向側壓力，不應將土的黏聚力略去，從而對馬斯頓理論進行修正，推導出新的計算公式。劉全林等[3]考慮管土之間的相互作用，確定了由管道變形引起的滑裂面的傾角和等沉面位置，建立了新的計算模型。婁奕紅等[4]假設涵頂土體形成楔形破裂體，考慮楔形體兩側受到的摩擦，然后計算楔形體對下方涵洞的土壓力。李永剛等[5]根據試驗和模擬所得回填土體沉降位移場，首次提出上埋式涵洞和溝埋式涵洞土壓力統一計算方法和兩種涵洞土壓力系數一致的變化規律，以及等沉面高度的變化規律。申文明等[6-7]根據自己的試驗結果，認為作用在涵頂面的土壓力并非均勻分布，通過假設涵頂面土壓力呈梯形分布，以此代人計算模型，得出淺埋深下相應的計算公式。馬強等[8-11]研究探討了在填土中設置EPS板、加筋材料、土工柵格減載之后的土壓力計算公式。

此外，還有學者通過大量現場試驗、模型試驗或數值模擬的方式來探討涵洞土壓力的變化規律及影響因素。如：顧安全[12]通過室內模型試驗研究了內外土柱間的沉降差與土壓力之間的關系，然后從變形條件出發，以彈性理論解為基礎，計算內外土柱間沉降差，最后以此求得涵洞土壓力。鄧國華等[13]利用有限單元法對填埋式涵洞的土壓力進行分析，發現隨著填土厚度的增大，垂直土壓力系數逐漸增大，并最終趨于穩定值：同時，還探討了涵洞兩側填土不均以及不同壓實層對垂直土壓力系數的影響。楊錫武等[14-15]結合模型試驗和ANSYS研究了不同邊界條件、跨徑、結構形式下垂直土壓力隨高度的變化。李永剛等[5，16]通過室內模型試驗和ANSYS分析了不同邊界條件、涵底寬度、涵洞結構形式下土壓力隨填土高度變化的規律以及涵頂面不同位置處土壓力的大小。陳保國等[17-18]運用FLAC2D和模型試驗驗證其設計的減載式涵洞減載效果，并推導出其上鋪設輕質柔性材料后涵頂豎向土壓力的計算公式。

縱觀這些研究成果不難發現，大多數學者只專注于涵頂面豎向土壓力進行研究，因此計算得到的土壓力分布往往呈均勻分布。然而，實際情況并非如此，涵頂面之上、填土表面之下的土柱中，豎向土壓力分布是具有一定變化規律的。

為了研究豎向土壓力的分布規律，以期達到和實際情況更為符合的效果，筆者以上埋式網涵為例，基于Marston理論，提出了新的分析計算模型。通過FLAC3D模擬得出內土柱豎向剪應力與分界面處豎向土壓力之間的關系式，再將此關系式代人上述計算模型，得到上埋式圓涵涵頂不同填土高度下內土柱中不同層面（包括涵頂面）豎向土壓力的分布規律。

1 涵頂土壓力分析計算模型

在以往以Marston理論為基礎的計算模型中，所取的計算單元是水平土層，并假設該土層上下部受到的豎向土壓力是均布的，但這一假設與實際情況并不符合。為此，本文仍以Marston理論為基礎，對豎向土壓力問題的求解進行改進。

1.1 模型建立

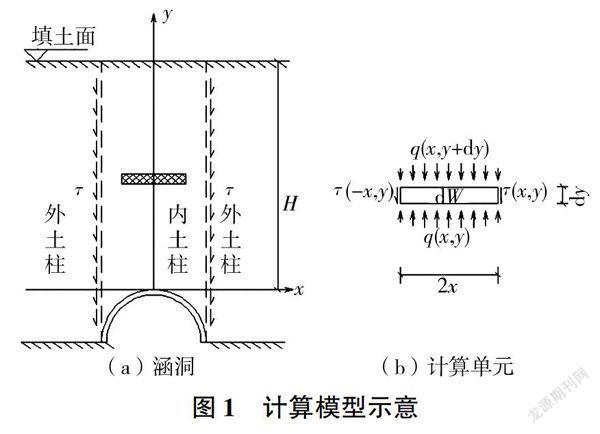
沿涵頂面水平向有為x軸正向，以涵頂點為原點，豎直向上為y軸正向，選取如圖1所示的水平計算單元，該單元關于y軸對稱，長度記為2x，寬度為dy。當2x等于涵洞外徑D時，即與Marston計算模型一致。

該單元所受上部豎向壓力分布為q（x，y+dy），下部豎向壓力分布為q（x，y），兩側所受剪切力分別記為τ（x，y）和τ（-x，y），自身重力記為dW。由于計算單元關于y軸對稱，因此兩側的豎向剪切力是相等的。另外其上下側受到的水平剪切力和兩側的水平土壓力可互相抵消，因此可以忽略水平方向的受力計算。

在本文計算模型中，y軸正方向是豎直向上的，恰與重力方向相反，因此后文所需研究的豎向土壓力統一設為負值。

1.2 計算假定

（1）涵洞地基視為剛體，即不考慮涵洞地基的變形。

（2）填土均勻，其沉降變形關于涵頂縱垂面對稱。填土中除涵頂面以外的任意一點均存在因土體沉降差異而產生的豎向剪切力。內外土柱的分界面為垂直平面，該分界面發生的相對沉降錯動使外土柱對內土柱產生豎直向下的剪切力。

（3）內土柱中豎向土壓力不是均勻分布，而是呈現曲線分布。

1.3 理論公式推導

鑒于上述所建模型關于y軸對稱的特點，可建立計算單元豎向受力平衡方程：

距涵頂面不同高度y處的剪切力與分界面處剪切力之比隨相對位置（距涵頂點水平距離x與涵洞半徑之比）的變化規律見圖3。可見，剪切力之比隨著距涵頂高度的增大而稍有減小，這表明距涵頂高度增大，填土沉降差變小，涵洞的存在對土體應力重分布的影響變小。同時，由于涵洞發生變形，在涵頂點附近填土沉降變大，因此在此區域內[即圖3中y=0，0≤x/（ D/2）≤0.4]該位置剪切力之比反而比其他層面剪切力之比小。到填土表面一直減小，直至趨近零，但并不完全等于零。若存在等沉面，則等沉面之上的填土沉降一致，填土內不存在豎向剪切力，剪切力與豎向土壓力比值為零。因此，可認為涵洞之上填土中不存在等沉面。

2 數值模擬

2.1 有限差分計算模型

使用有限差分軟件FLAC3D構建計算模型，由于所研究的問題不涉及沿涵洞走向的變化，可視為平面應力應變問題，因此僅取單位長度的涵洞模型，模型底部寬B=50 cm，厚度則為單位長度1 cm，其中涵洞外徑D= 10Cm，涵洞厚度1= 0.2 cm。填土為粒徑小于2mm的中細砂，本構模型為Mohr - Coulomb模型：涵洞材料為C30混凝土，采用彈性本構模型：填土與涵洞間設置接觸面，摩擦系數為0.3。模型中填土和涵洞的強度參數取參考文獻[16]中室內模型試驗的材料參數，主要參數見表1。

2.2 模型計算結果分析

2.2.1 數值模擬與模型試驗結果對比

在文獻[16]的模型試驗中，測得涵洞上覆填土高度H為10、30、50、70、90Cm情況下涵頂面不同位置處豎向土壓力（向上為正，向下為負）。應用本文方法模擬計算了如上填土高度下涵頂面豎向土壓力，其與試驗結果的對比見圖4。

可見，FLAC3D模擬的涵頂面豎向土壓力分布規律與室內試驗結果一致，皆為涵洞兩側豎向土壓力小，涵頂點處壓力最大。FLAC3D模擬計算得到的不同填土高度下各檢測點豎向土壓力與室內試驗實測值相差不大，這表明數值模擬結果是可信的。

2.2.2 填土內應力變化分析

基于填土高度H為70 cm的數值模型，對涵洞上方填土內部豎向土壓力和剪切力的變化規律進行分析。模型范圍選取涵頂面至其上方30Cm填土區域。繪制距涵頂點不同高度y處填土應力分布曲線，見圖5、圖6。

可見，填土內的土壓力由上至下逐漸由均勻分布變為曲線分布，其特征為中間大、兩側小，且越靠近涵頂面，其增大幅度越大。這表明愈接近涵頂面，豎向土壓力的集中效應愈明顯：在涵頂面由于豎向土壓力過大，因此涵洞頂點發生變形，產生向下的位移。對于剪切力，涵頂點豎直面上剪切力基本為零：由涵頂點往外，剪切力先變大、后變小，在內外土柱的分界面處剪切力基本達到最大，再往外則逐漸減至零。這說明從中心到兩側，填土不均勻沉降先增大后減小。越靠近涵頂面，剪切力變化幅度越大。

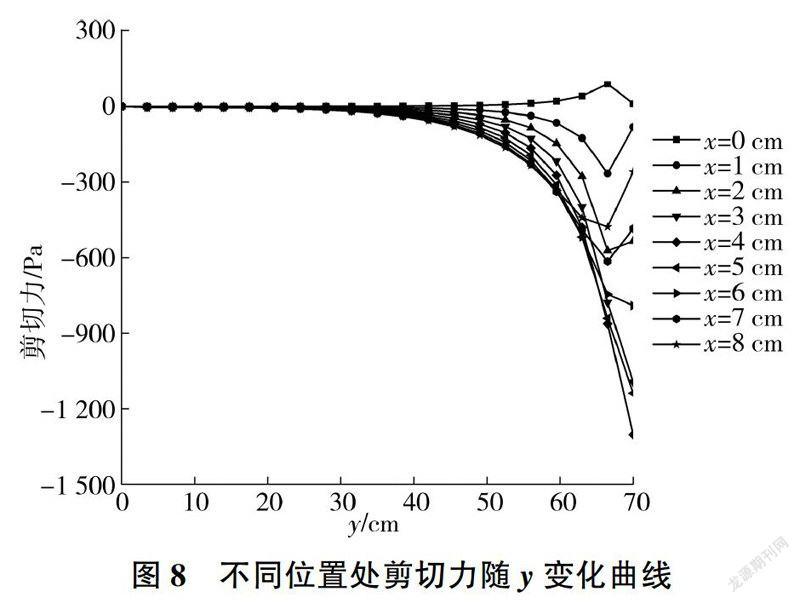
本文構建的模型沿涵洞縱垂面對稱，故選取涵頂點右側8 cm的區域，每隔1 cm對這一垂面上豎向土壓力和剪切力隨y的變化曲線進行繪制，見圖7、圖8。

可見，豎向土壓力在y≤50 c：m時基本呈線性增長，y>50 cm時呈現非線性增長，且其在涵洞上方的內土柱中增長幅度變大，在外土柱中增長幅度變小，原因是外土柱中壓力轉移至內土柱中。填土內的剪切力遠小于豎向土壓力，隨y增大，剪切力呈非線性變化，基本在內外土柱的分界面處達到最大。在靠近涵頂點區域，由于涵洞向下發生變形，填土產生向下位移，差異沉降變小，因此剪切力反而稍有減小。

3 計算結果對比

3.1 涵頂面豎向土壓力分布對比

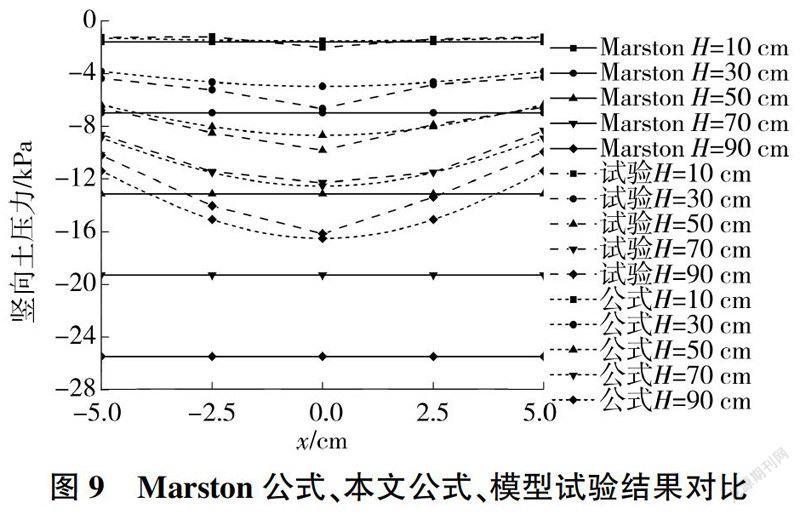
根據上文推導得出的公式計算不同填土高度（H=10、30、50、70、90Cm）下涵頂面的豎向土壓力，并與前人的模型試驗及經典的Marston公式計算結果進行對比分析，如圖9所示。

由圖9可見，本文提出的公式計算所得的不同填土高度下涵頂面豎向土壓力分布與模型試驗結果較為吻合，均表現出涵頂面豎向土壓力由涵洞兩側向涵頂點呈逐漸增大的趨勢。當填土高度較小時，無論是公式計算，還是模型試驗結果，涵頂面土壓力分布曲線均較為平緩：當填土高度較高時，這兩種方法得出的分布曲線呈現明顯的下凸形，且填土高度越高，下凸的幅度就越大。而經典的Marston公式未能反映填土豎向土壓力不均勻分布的特征，而且其值偏離模型試驗結果比較大。

3.2 填土內豎向土壓力分布對比

由于前人的模型試驗未測得填土內部不同位置處豎向土壓力分布，因此本文僅比較數值模擬與公式計算同一填土高度下（H= 70Cm）內土柱中不同層面（y=5、10、15、20、25、30 cm）的豎向土壓力分布（如圖10所示）。

由圖10可見，兩者的計算值較為吻合，距涵頂面較高層面的豎向土壓力分布曲線較為平緩，而距涵頂面較近時豎向土壓力曲線呈現出明顯的下凸形態。這也說明，距涵頂面越近涵洞的頂托作用以及對土體豎向變形的約束作用越強，涵頂點土壓力集中效應越大。

3.3 幾種豎向土壓力算法計算結果對比

以往的關于涵頂土壓力的計算方法如經典的Marston公式、《公路橋涵設計通用規范》（以下簡稱公路規范）、《鐵路橋涵設計規范》（以下簡稱鐵路規范）等，大多將涵頂面豎向土壓力視為均布力來處理。其中公路規范采用土柱法計算涵頂土壓力，即P_v=γH；鐵路規范則采用集中系數法，即p_v=kγH，其中系數k是由比值H/D（H為填土高度，D為涵洞外徑）進行查表確定。

為了進一步驗證本文所提方法的合理性，本節將模型試驗、數值模擬和本文公式算得的涵頂面平均豎向土壓力與經典的Marston公式、公路規范、鐵路規范算得的結果進行了比對（見圖11）。同時，還比較了不同填土高度時這幾種方法算得的涵頂點豎向土壓力（見圖12）。可以看出：

（1）在埋深較淺時，Marston公式計算值較符合實測值，但是隨著填土高度的增大，其值急劇增大，遠大于實測值。原因是Marston公式假設涵頂上方內外土柱之間因沉降而產生了一個處于極限狀態的滑動面，但是從本文數值模擬結果來看，很明顯不存在這樣的滑動面，內外土柱分界面處剪切力與豎向土壓力之比并非定值，而是從涵頂面至填土表面呈逐漸減小的趨勢。

（2）公路規范中土柱法計算所得的涵頂面平均土壓力值較模型試驗值小：鐵路規范采用的集中系數法算得的涵頂面平均土壓力較模型試驗、數值模擬及本文公式算得的平均豎向土壓力都大，但其算得的涵頂點處豎向土壓力小于這三者計算出的涵頂點豎向土壓力。

（3）模型試驗、數值模擬以及本文公式計算的結果，無論是涵頂面的平均土壓力值，還是涵頂點處豎向土壓力，都比較接近。

4 結語

本文在Marston理論的基礎上，提出了一種計算上埋式涵洞上覆土壓力的新方法。該方法綜合了理論解析公式的推導與數值模擬技術，使算得的土壓力值與實測值更為吻合。將本文方法與前人涵洞模型試驗的結果、FLAC3D數值模擬結果、鐵路及公路規范中的方法進行對比，得到以下結論：

（1）涵頂填土中，距涵頂面不同高度的層面（包括涵頂面）豎向土壓力并非均勻分布，而是表現為中間大、兩側小，涵頂中心土壓力集中，并且填土高度越高、距涵頂面越近，集中效應越大。

（2）在內外土柱的分界面不存在處于極限狀態的滑動面，從涵頂面到填土表面，在分界面處剪切力逐漸變小，同時剪切力與豎向土壓力的比值也逐漸減小。

（3）本文提出的計算方法與模型試驗的實測結果較為接近，能較好地反映涵頂填土內豎向土壓力的分布及變化規律，且計算出來的涵頂面豎向土壓力平均值在鐵路規范與公路規范計算所得的平均豎向土壓力之間，而經典的Marston公式計算出來的結果遠大于模型試驗值。

本文分析計算基于網形涵洞，最后推導出來的公式僅限于計算圓形涵洞之上填土的豎向土壓力，然而不同涵洞形式對豎向土壓力分布影響很大，對于如箱形、拱形等形狀的涵洞則不適用。本文公式推導時對不同層面處剪切力分布規律進行了一定簡化，認為其分布規律由填土面到涵頂面保持一致，綜合考慮擬合出相關函數，但這與實際情況有一定差異，計算結果誤差隨填土高度增加而變大。另外，計算模型未涉及涵洞與地基的變形，而在數值模擬和實際應用中，涵洞承受的土壓力過大會發生變形，涵頂點附近填土向下位移，涵頂面豎向土壓力集中程度有所變弱。并且，本文數值模擬選用的填土材料為無黏性土，并未考慮黏聚力的影響。這些不足之處還需在后續工作中展開研究。

參考文獻：

[1]

MARSTON A.The Theory of External Loads on Closed Con-duits in the Light of the Latest Experiments[J].HighwayResearch Board Proceedings， 1930，9：138- 170.

[2] 曾國熙，土壩下涵管豎向土壓力的計算[J].浙江大學學報（工學版），1960（1）：79-97.

[3]劉全林，楊敏.上埋式管道上豎向土壓力計算的探討[J].巖土力學，2001，22（2）：214-218.

[4]婁奕紅，王秉勇.涵洞頂填土壓力的計算分析[J].巖土力學，2003，24（3）：475-478.

[5] 李永剛，張善元.矩形溝埋涵洞頂部垂直土壓力試驗和理論研究[J].巖土力學，2008，29（4）：1081-1086.

[6] 申文明，邊學成，唐曉武，等.低填方上埋式管涵土壓力的模型試驗和理論研究[J].巖土工程學報，2010，32（7）：1017 -1022.

[7] 申文明.埋地管涵一土相互作用及管涵結構橫縱向受力特性研究[D].杭州：浙江大學，2011：183-185.

[8] 馬強.高填方涵洞受力特性及新型格柵減載方法研究[D].武漢：華中科技大學，2011：105 - 106.

[9] 李盛，王起才，馬莉，等.黃土地區高填土明洞土拱效應及土壓力減載計算[J].巖石力學與工程學報，2014，33（5）：1055-1062.

[10] 李盛，王起才，馬莉，等.高填黃土明洞土拱效應及土壓

力減載模型分析[J].土木_廠程學報，2014（7）：118-125.

[11] 李盛.高填黃土明洞卸載結構的垂直土壓力特性和計算方法研究[D].蘭州：蘭州交通大學，2015：130-131.

[12]顧安全.上埋式管道及洞室垂直土壓力的研究[J].巖土工程學報，1981，3（1）：3-15.

[13] 鄧國華，邵生俊.填埋式涵洞上覆土壓力的有限元分析[J].巖石力學與工程學報，2004，23（增刊1）：4356-4360.

[14] 楊錫武，張永興.公踣高填方涵洞土壓力變化規律及計算方法研究[J].土木工程學報，2005（9）：119 - 124.

[15] 楊錫武，張永興.山區公路高填方涵洞的成拱效應及土壓力計算理論研究[J].巖石力學與工程學報，2005，24（ 21）：89-95.

[16] 李永剛.溝埋式和上埋式涵洞土壓力統一計算理論研究[D].太原：太原理工大學，2009：96-97.

[17] 陳保國，宋丁豹，王云輝，等.減載式剛性涵洞減載機理與受力特性研究[J].華中科技大學學報（自然科學版），2016，44（4）：79-84.

[18] CHEN B，SONG D， MAO X， et al.Model Test and Nu-merical Simulation on Rigid Load Shedding Culvert Back-filled with Sand [J]. Computers and Geotechnics， 2016，79：31- 40.