基于流管法的面積波及效率計算方法研究

邢翠巧 尹洪軍 李興科 劉岢鑫 付京

摘要：中國已開發的大多數油田，經過多年的加密調整和注水開發，目前已處于高含水或高采出程度階段，開采和穩產難度越來越大。因此，對注水開發油田進行水驅面積波及系數的研究意義重大。根據注水油田的基本特點，基于流管法建模基本原理，建立了五點法流管模型，利用Beckley-Leverett方程，結合單元分析法和流線積分法，對注水油田五點法井網面積波及效率的計算公式進行了詳細推導，繪制并分析了面積波及系數和采出程度隨時間的變化曲線。結果表明：當無流管突破時，注水油田的面積波及系數隨時間的增加而線性增大；當主流管突破見水后，波及系數增大程度越來越慢，最后趨于平緩。當油田被注入水完全波及后，繼續利用注水提高采收效果的作用很小，水驅效率明顯降低。研究結果對于注水油田面積波及系數的求解及水驅動態開發規律的研究具有借鑒意義。

關鍵詞：滲流力學；流管法；面積波及效率；水驅動態開發；流線積分法

中圖分類號：TE344文獻標志碼：Adoi： 10.7535/hbgykj.2018yx04001

水驅面積波及系數是描述油田開發效果的重要參數之一，提高水驅波及面積是提高原油采收率的重要手段，代表了水驅過程中注水驅替的好壞程度，對于研究、計算不同注采井網類型的水驅驅油效率和最終采收率等參數具有重要意義。所以，雖然面積波及系數的計算難度大，但是國內外已有很多學者對其進行了研究[1-3]。

用來研究水驅規律的最早的實驗技術方法是電解模型，由MUSKAT等[4]于1934年最先提出，用電流來演示穩定滲流。隨著對水驅滲流規律的不斷研究，吸墨紙式模型和明膠模型相繼出現，但是這些模型仍是電解模型的延續。DOYLE等[5]利用流線位置相似的特性，結合電位模型研究獲得的技術，生成了一個簡化網絡，從流線定義出發，擴展了流動通道的形狀。他們利用這種方法進行了經濟可行性研究，其中對于儲層的最佳模式和密度可以有多個選擇，并通過與實驗室模型相比較，建立了流度比的計算程序。尹洪軍等[6]對基于流管法的注水油田開發進行了數值模擬研究，通過建立“一注一采”的概念模型，求解并繪制該概念模型的流管法滲流圖版，給出了水驅油田動態開發分析方法，對于準確描述和評價小層的動用程度和水驅波及效率具有重要的應用意義。目前，對于注水油藏水驅動態及流體滲流規律的研究不斷深入，研究方法主要包括油藏工程方法、實驗方法和數值模擬方法[7-8]。牛彥良等[9]通過對井網系數、驅油效率和波及系數等因素的分析，結合非達西滲流理論，研究了注水油藏水驅采收率計算方法。范江等[10]運用概率論和量綱分析方法建立了波及系數計算模型。該方法中有大量的統計學公式，難以應用到礦場分析中，不利于推廣。近年來國內外學者針對注水油藏提出了一些計算面積波及系數的公式，給出了面積波及系數的計算方法[11-15]，但計算公式應用的大多是標定值，是通過與地質或井網參數回歸得到的，并沒有考慮到其他參數對面積波及系數的影響，因此，在一定程度上存在不合理性。

流線模擬最大的優勢就是計算速度快，且精度高，具有良好的可視性。流線模擬的計算過程都是沿流線進行的，在每一個網格尺寸內可以直觀地描述流體從何處來，將到何處去，這就相當于加密網格的情形，但是并沒有增加大量的計算量。因此，本文考慮將流線方法結合到五點法井網的注水驅替問題中，給出水驅過程中面積波及效率等動態參數的變化特征。

1流管法

流管法就是假設在注水驅替過程中，油藏的物理驅替機理是可以用注采井之間的一根根不相交的流管來表示。流線表示的就是流體過程中的流動軌跡，兩根流線組成1根流管，在研究區塊內的注采井之間有規律的分布著多根流管。本文用形狀因子來考慮每一根流管的形狀，其大小與地層性質等有關。

面積注水是指將注水井和采油井按一定的幾何形狀和密度均勻地布置在整個開發區上進行注水和采油。五點井網是當注采比為1時的井位布置形式，如圖1所示。

模型假設條件：

1）油層是均質、等厚的單一油層；

2）油井和水井之間由流管組成，流管中的流體為水驅油過程；

3）水驅油過程仍然遵循已經確定的多孔介質中均質流體穩定滲流時的流線；

4）不考慮地層巖石及流體的壓縮性；

5）不考慮毛管力和重力的作用；

6）油井以定產量生產。

根據以上假設條件，在每一口油井與水井之間建立多根流管，通過圖1及五點法井網流體滲流特征及對稱性的分析，取五點法井網中的1/8單元作為計算單元，見圖2。

在圖2中，油、水井半徑為rw，油、水井距為l，油藏厚度為h。任意一根三角流管的夾角為Δα，流管角平分線由對稱的L1和L2組成，它與主流線的夾角為α。沿三角流管中線上的位置表示的是注水驅替過程中流管內前緣移動的位置，用坐標ξ表示。

2數學模型

根據上述所建立的流管模型，研究對應的數學模型，可以將水驅油藏五點法井網的二維兩相驅替問題簡化為若干個一維兩相滲流問題，以降低計算求解的難度，且有利于實現后期的編程計算。

第i根流管的角平分線與主流線的夾角為α（i），則

α（i）=Δα·（i-12）=π4N（i-12）。 （1）

流管角平分線的長度為

L（i）=lcos α（i） 。 （2）

以下將L（i）簡記為L。

角平分線上某一位置ξ處的橫截面積為

A（ξ）=2tanΔα2h·ξ，rw≤ξ≤L2；

2tanΔα2h·（L-ξ）， L2<ξ≤L-rw。（3）

在確定了流管的基本參數之后，給出了水驅油藏五點法井網面積波及系數的求解方法：模型中有N根流管，并且每根流管都是由2個對稱的等腰三角形拼接而成，流管流動區域所占的面積表示的是去除注水井和采油井所占的面積后其余的面積。每一根流管之間均互不交叉，第i根流管可流動區域的面積記為Stube（i），該流管中劃分成的每個小塊的面積記為Scell（i），所有流管可流動區的總面積記為Stotal。將每根流管等體積的分為2M份，根據幾何關系，可得：

Stube（i）=2tanΔα2（14L2-r2w），（4）

Scell（i）=Stube（i）2M， （5）

Stotal=∑Ni=1Stube（i）。 （6）

記第i根流管內已經波及到的區域的面積為SAC（i），前緣Lf（i）處于第k（i）個小塊內（以下將Lf（i）簡記為Lf），計算SAC（i）需要分不同的情況進行討論，具體如下。

1）當前緣未過流管中線半長時

SAC（i）=Scell（i）（k-1）+Strapezoid， （7）

其中

Strapezoid=2tan（Δα2）（yk-1+Lf）·Lf-yk-12。

2）當前緣過流管中線半長但未突破時

SAC（i）=Scell（i）（k-1）+Strapezoid， （8）

其中

Strapezoid=2tan（Δα2）[（L-yk-1）+

（L-Lf）]·Lf-yk-12。

3）當流管突破時

SAC（i）=Stube（i）。 （9）

綜上所述，整理得到

SAC（i）=

Scell（i）（k-1）+tan（Δα2）（L2f-y2k-1），rw≤Lf≤L2；

Scell（i）（k-1）+tan（Δα2）（2L-yk-1-Lf）·

（Lf-yk-1），L2Stube（i），Lf≥L-rw。（10）

因此可得：

φ=∑Ni=1SAC（i）Stotal， （11）

式中φ為面積波及效率。

利用式（11）計算不同時刻對應的波及面積，進而可以計算得到面積波及系數的值，但是計算過程中涉及到滲流阻力、不同時刻的前緣位置及前緣含水飽和度值等參數的計算。

計算滲流阻力：

R（i）=1K（i）[∫LfrwdξA（ξ）（Krwμw+Kroμo）+

∫L-rwLfdξA（ξ）Kro（Swc）μo] ，（12）

式中：Swc為束縛水飽和度；μw為水相黏度，mPa·s；μo為油相黏度，mPa；Krw為水相相對滲透率；Kro為油相相對滲透率；rw為井筒半徑，m。

計算各根流管分配到的注入量：

q（i）=Q1R（i）∑Ni=11R（i），（13）

式中Q為整個單元的總注入量，m3。

計算水驅前緣位置：

Lf=r2w+f′w（Swf）Witan（Δα2）h，rw≤Lf≤L2；

L-L2-C，L2

1）根據流管法的基本原理，建立水驅油藏的五點井網三角流管模型，可以將平面的二維兩相驅替問題轉換為一維兩相驅替問題，這樣就從計算方法上大大降低了求解難度。

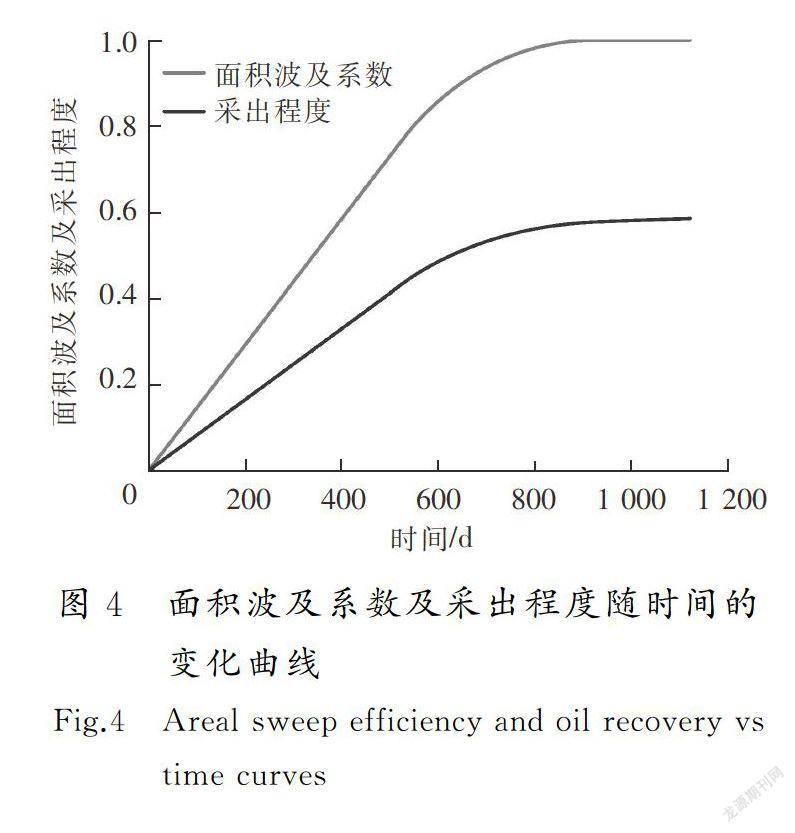
2）在沒有流管突破時，注入水在油藏中均勻波及，波及系數隨時間的增加而線性增大；當主流管突破后，油井見水，波及系數增大的程度越來越慢，直至趨于平緩，表明注入水完全波及整個井網單元，注水對提高原油采收率的作用已經十分微弱，水驅效率明顯降低。

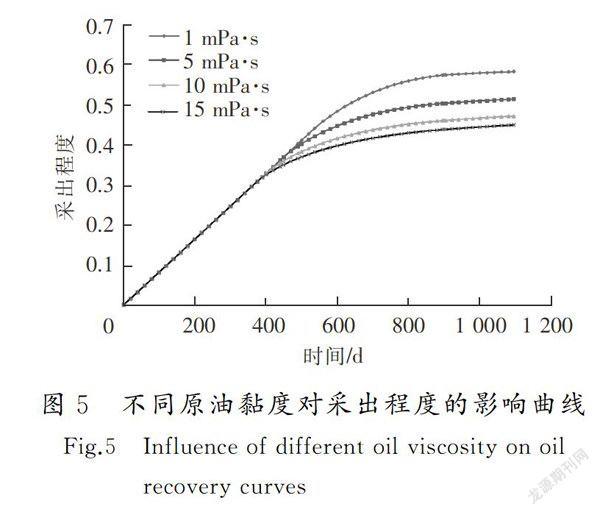
3）流度比越大，注水開發油藏的驅油效果越差，通過提高注入液黏度來降低流度比，可以更有效地提高水驅開發的效果，進而增加原油采收率。

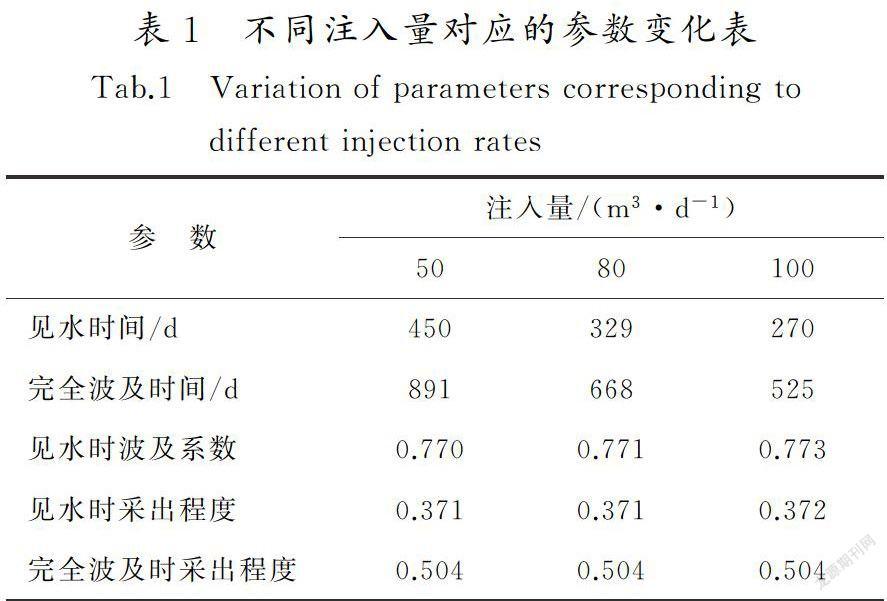
4）當油田進行注水驅替時，在注入壓力不超過巖石破裂壓力的情況下，可以通過適當增大注入量的方式來提高原油采油率，加快油田采收速度。

利用流管法求解油藏動態參數的方法快速有效，未來會得到廣泛的應用。本文考慮的是規則五點法井網，對于油田現場的復雜不規則井網，還需進一步研究流線的分布，以便運用流管法求解，獲得有關的油田動態參數，指導油田后期開發，有效提高原油采收率。

參考文獻/References：

[1]沈非， 程林松， 黃世軍， 等. 基于流管法的普通稠油水驅波及系數計算方法[J]. 石油鉆采工藝， 2016， 38（5）： 645-649.

SHEN Fei， CHENG Linsong， HUANG Shijun， et al. Calculation of sweep efficiency for water flooding development of conventional heavy oil using the stream-tube method[J]. Oil Drilling and Production Technology， 2016， 38（5）： 645-649.

[2]計秉玉， 李莉， 王春艷. 低滲透油藏非達西滲流面積井網產油量計算方法[J]. 石油學報， 2008， 29（2）： 256-261.

JI Bingyu， LI Li， WANG Chunyan. Oil production calculation for areal well pattern of low permeability reservoir with non-Darcy seepage flow[J]. Acta Petrolei Sinica， 2008， 29（2）： 256-261.

[3]HIGGINS R V， LEIGHTON A J. A computer method to calculate two-phase flow in any irregularly bounded porous medium [J]. Journal of Petroleum Technology， 1962，14（6）： 679-683.

[4]MUSKAT M， WYCKOFF R D. A theoretical analysis of water flooding networks[J]. Transactions of the AIME， 1934，107（1）：62-76.

[5]DOYLE R E， WURL T M. Stream channel concept applied to water flood performance calculations for multi well， multi zone， three-component cases [J]. Soc Pet Eng AIME Pap， 1971，spe2653（3）： 373-380.

[6]尹洪軍， 付瑩， 王美楠. 基于流管法低滲透油藏開發數值模擬研究[J]. 石油化工高等學校學報， 2015， 28（3）： 61-64.

YIN Hongjun， FU Ying， WANG Meinan. Numerical simulation research for low-permeability reservoirs based on stream tube model [J]. Journal of Petrochemical Universities， 2015， 28（3）： 61-64.

[7]王強， 計秉玉， 聶俊. 聚合物驅油過程中不同粘度比情況下波及系數計算方法 [J]. 石油與天然氣地質， 2014， 35（4）： 551-555.

WANG Qiang， JI Bingyu， NIE Jun. Calculation methods of sweep efficiency under different viscosity ratios for polymer flooding process[J]. Oil and Gas Geology， 2014， 35（4）： 551-555.

[8]NELSON R A. Geologic analysis of naturally fractured reservoirs [M]. Tesas： Goulf Publishing Company， 1985.

[9]牛彥良， 李莉， 韓德金， 等. 低滲透油藏水驅采收率計算新方法[J]. 石油學報， 2006， 27（2）： 77-79.

NIU Yanliang， LI Li， HAN Dejin， et al. A new method for calculation recovery factor of water drive in low permeability reservoir[J]. Acta Petrolei Sinica， 2006， 27（2）： 77-79.

[10]范江， 張子香，扎拉杜新А Б. 非均質油層波及系數計算模型[J]. 石油學報， 1993， 14（1）： 92-97.

FAN Jiang， ZHANG Zixiang， ZALADUXIN А Б. Calculation model of sweep efficiency for heterogeneous reservoir [J]. Acta Petrolei Sinica， 1993， 14（1）： 92-97.

[11]郭粉轉， 唐海， 呂棟梁， 等. 滲流啟動壓力梯度對低滲透油田五點井網面積波及效率的影響[J]. 大慶石油學院學報， 2010， 34（3）： 65-68.

GUO Fenzhuan， TANG Hai， LYU Dongliang， et al. Effects of seepage threshold pressure gradient on areal sweep efficiency for five-spot pattern of low permeability reservoirs [J]. Journal of Daqing Petroleum Institute， 2010， 34（3）： 65-68.

[12]朱圣舉， 朱潔， 安小平， 等. 低滲透油藏菱形反九點井網面積波及系數研究[J]. 重慶科技學院學報（自然科學版）， 2013， 15（2）： 80-84.

ZHU Shengju， ZHU Jie， AN Xiaoping， et al. Research on areal sweep efficiency for rhombus invert 9-spot areal well pattern of low permeability reservoir [J]. Journal of Chongqing University of Science and Technology （Natural Science Edition）， 2013， 15（2）： 80-84.

[13]喻秋蘭， 唐海， 呂棟梁， 等. 平面非均質性對面積波及系數的影響[J]. 重慶科技學院學報（自然科學版）， 2011， 13（5）： 59-61.

YU Qiulan， TANG Hai， LYU Dongliang， et al. On the Effect of areal heterogeneous on areal sweep efficiency[J]. Journal of Chongqing University of Science and Technology （Natural Science Edition）， 2011， 13（5）： 59-61.

[14]蒲軍， 劉傳喜， 尚根華. 基于流線積分法的注水井網非穩態產量模型[J]. 西南石油大學學報（自然科學版）， 2013， 15（2）： 80-84.

PU Jun， LIU Chuanxi， SHANG Genhua. Non-steady water flooding production model of areal well pattern based on flow line integral method [J]. Journal of Southwest Petroleum University （Science and Technology Edition）， 2013， 15（2）： 80-84.

[15]DING D Y， FARAH N， BOURBIAUX B， et al. Simulation of matrix-fracture interaction in low permeability fractured unconventional reservoirs[C]//SPE Reservoir Simulation Conference. [S.l.]：[s.n.]， 2017： 1-29.