一種基于自適應相似矩陣的譜聚類算法

王貝貝 楊明 燕慧超 孫笑仙

摘?要：為了消除在構建譜聚類算法的相似矩陣時，高斯核函數中尺度參數的波動影響，構建了一種自適應相似矩陣，并應用到譜聚類算法中。自適應相似矩陣中數據點間的距離度量采用測地距離算法，相距較近的兩點間的距離近似于歐氏距離，相距較遠的兩點則先根據歐氏距離得到每個數據點的k個近鄰點，然后累加近鄰點的測地距離，由此得到每對數據點間的最短距離。兩點間的局部密度用共享近鄰的定義來表示，更好地刻畫了數據集的本征結構。在5個人工數據集和國際通用UCI數據庫中的5個真實數據集上進行實驗。實驗結果表明，所提算法的聚類準確率高于對比算法的準確率，對復雜分布數據有很強的自適應能力。研究成果為數據挖掘及機器學習提供了思路和方法。

關鍵詞：應用數學;相似矩陣;譜聚類;密度;測地距離

中圖分類號：TP391???文獻標志碼：A

doi： 10.7535/hbgykj.2018yx02001

A spectral clustering algorithm based on

adaptive similarity matrix

WANG Beibei1， YANG Ming1， YAN Huichao1， SUN Xiaoxian2

（1.School of Science， North University of China， Taiyuan， Shanxi? 030051， China;

2.Faculty of Science and Technology， Communication University of China， Beijing 100024， China）

Abstract：

In order to eliminate the fluctuation of the scale parameters in gaussian kernel function in constructing the similarity matrix of spectral clustering algorithm， a self-adaptive similarity matrix is constructed and applied in the spectral clustering algorithm. Geodesic distance measure is used in distance measure between data points in the adaptive similarity matrix. Distance between points closer to each other is approximately equal to the Euclidean distance， while for distance between two points farther away， each data's k-nearest neighbors are firstly obtained by Euclidean distance， then the geodesic distances of the nearest neighbors are accumulated， thus， the shortest distance between each pair of data can be get. The local density of two points is defined by the shared neighbor， reflecting the eigen structure of the data set better. Finally， experiments on both five artificial data sets and five UCI data sets show that the proposed method is more accurate than the others， and has a strong adaptive ability for complex distribution data. The research provides idea and method for data mining and machine learning.

Keywords：

applied mathematics; similar matrix; spectral clustering; density; geodesic distance

聚類分析在數據挖掘和機器學習領域都有非常廣泛的應用，它是根據數據點之間相似度的不同，將待聚類的數據集劃分成不同類的方法，源于很多領域，包括數學、計算機科學、統計學、生物學和經濟學[1]。在不同的應用領域，很多聚類技術都得到了發展，這些技術方法被用作描述數據，衡量不同數據源間的相似性，以及把數據源分類到不同的簇中。其中譜聚類算法[2]是在譜圖劃分理論基礎上發展起來的，不僅能識別任意形狀的樣本空間，應用在非塊狀和非凸形數據的聚類問題上，而且收斂于全局最優解，目前已在圖像分割[3]、文本挖掘[4]、計算機視覺[5]等領域得到較好的應用。

譜聚類算法的核心是對特征向量的聚類，而該特征向量是由待聚類數據集的相似矩陣（拉普拉斯矩陣）特征分解得到的。因此，譜聚類算法性能的好壞取決于構建的相似矩陣。然而傳統譜聚類算法中的高斯核函數只考慮數據點間的歐式距離，符合局部一致性，不符合全局一致性。文獻[6]提出一種近鄰自適應局部尺度的譜聚類算法，局部尺度的值取為樣本點k個近鄰的距離和，解決了單一全局尺度參數局限的問題。文獻[7]用共享近鄰表征兩兩數據點間的局部密度，并應用于相似度度量，提出一種基于共享近鄰的自適應譜聚類算法（SNN-ASC）。文獻[8]提出一種密度敏感的相似性度量，并結合特征間隙，能根據數據的實際分布情況進行聚類。文獻[9]提出一種基于無參相似矩陣的譜聚類，考慮數據集中點的密度、距離、連通性3個信息，然后構造出一個無參相似圖并構建相應的相似矩陣。文獻[10]采用一種基于k-means算法的密度估計法構造相似矩陣，其過程提高了密度估計的準確性，但是卻需要6個超參數，且當數據集中有較相似的結構時，聚類效果不理想。

本研究在分析數據特征的基礎上，構建了一種自適應的相似矩陣。選用測地距離函數表征數據間的距離度量，相距較近的兩點間的距離近似于歐氏距離，相距較遠的兩點則先根據歐氏距離得到每個數據點的k個近鄰點，然后累加近鄰點的測地距離，這樣便得到了每對數據點間的最短距離，不僅消除了高斯核函數中尺度參數的波動影響，而且克服了歐式距離的局限性。根據每個點所處鄰域的稠密程度，用兩點間的共享近鄰數來表征，進而得到待聚類數據點的[WT]基于測地距離和共享近鄰數的相似度，應用到譜聚類算法中。最后在密度分布不均以及非塊狀（弧形、圓圈形、線形等）的人工數據集上、通用國際UCI實際數據集上都進行實驗，并與k-均值算法（k-means）和基于規范化拉普拉斯矩陣的譜聚類算法（NJW）進行比較。結果表明，本文算法對復雜分布數據有更強的自適應能力和更高的準確率。

1 譜聚類算法的基本原理及現存問題

本節以傳統的譜聚類算法為基礎進行分析，譜聚類的實現方法有很多種，其中主要研究對象是NJW譜聚類算法，其具體實現過程可以歸納為4步：

譜聚類算法的主要技巧是通過拉普拉斯矩陣將數據點映射到一個較低維的空間。在低維的數據空間中，數據點具有更好的聚類特性且滿足一致性假設。

1）局部一致性 在空間位置上相鄰的數據點具有更高的相似性;

2）全局一致性 同一結構上（同類中）的數據點具有更高的相似性。

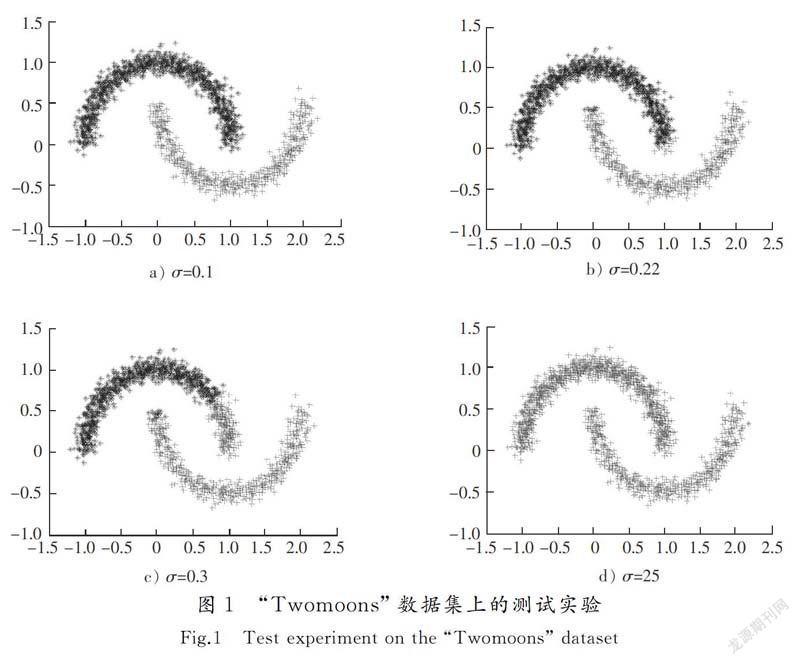
傳統譜聚類算法中的高斯核函數[WT]exp（[SX（]-‖xi-xj‖22σ2[SX）]）只考慮數據點間的歐式距離，符合局部一致性，不符合全局一致性，且當尺度參數σ[WT]選取不同值時，聚類結果也不相同。圖1顯示了在歐氏距離的測度下，選取不同的尺度參數時在“Twomoons”數據集上的測試實驗。

可以看出，尺度參數[WTBX]σ取不同數值時得到的聚類結果也不相同。當σ=0.1時，聚類結果是最理想的;當σ=0.22時，聚類結果出現了微小的偏差;當σ=0.3時，聚類結果誤差較大;當σ=25時，聚類結果完全錯誤。針對不同的[WT]數據集，尺度參數的選擇范圍也不相同。

2 基于測地距離和密度的自適應譜聚類算法

2.1 測地距離

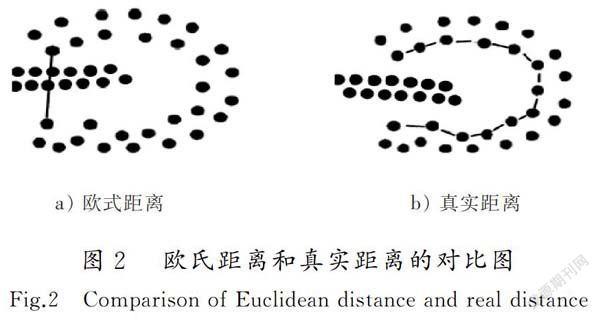
在構建相似度測度時，距離函數占著至關重要的地位，沒有任何一種距離測度適合所有的數據集。傳統的歐式距離做測度度量時，只是單純的計算連接兩點的直線段的長度，如圖2 a），如若這兩點間存在障礙物或者說存在另一個結構中的樣本，此時的歐式距離是沒有實際意義的，這就是歐氏距離的局限性，圖2 b）是要得到的真實距離效果。越來越多的文獻都在做距離測度方法的改進，文獻[11]提出用有效距離函數代替傳統的地理距離函數，刻畫了目標樣本和其他所有數據樣本之間的距離信息，具有全局特性。文獻[12]提出一種基于電阻距離的中文文本譜聚類算法，把文本表示成二分圖形式，使用電阻值表示兩點間的相似度值，電阻值隨著節點間路徑減小而減小，從而計算出任意節點間的有效電阻距離更具有實際意義。

測地距離是數學形態學中的一個重要概念，最早是TENENBAUM等[13]在研究非線性降維時提出的，能很好地表示流形結構上樣本之間的真實距離。如圖3中的點[WTBX]A，B，C位于同一流形結構上，[WTBX]dAB，dAC，dBC分[WTBX]別表示點A和點B，點A和點C，點B和點C之間的歐式距離，[WTBX]gAC，gBC[WTBX]分別表示點A和點C，點B和點C之間的測地距離，假設點A和點B之間存在障礙物不能直接計算歐式距離，在同一結構中，從點A到達點B的路徑有很多條，最短的一條測地弧的長度稱為點A和點B間的測地距離。由圖3可以看出，當A，C兩點非常近時，取[WTBX]gAC≈dAC，[WTBX]即認為A，C兩點間的測地距離近似等于其歐氏距離。而當A，B兩點之間相距較遠時，則取兩點間的測地距離等于其近鄰點間的測地距離累加和，即[WTBX]gAB=gAC+gCB≈dAC+dCB，從而得到待聚類數據集中每對數據點之間的實際最短距離。

測地距離具體算法如下。

1）輸入數據集X=[x1，x2，…，xi，…，xn]，根據歐式距離計算點xi的k個近鄰。

2）初始化測地距離：

dG（xi，xj）=

d（xi，xj），點xj是點xi的k近鄰之一，∞ ，其他，

其中d（xi，xj）表示的是點xi和點xj之間的歐氏距離。

3）計算任意兩點間最短路徑：

For m=1：n

dG（xi，xj）=min{dG（xi，xj），

dG（xi，xm）+dG（xm，xj）}

End

2.2密度

僅用距離來描述數據之間的相似性遠遠不夠，特別是對密度分布不均的數據集，好的相似性度量不僅不依賴于尺度參數σ，而且能夠根據每個點所處鄰域的稠密程度得到正確的聚類結果。JARVIS等[14]曾提出一種基于共享近鄰相似度測量方法的聚類，本研究借鑒其中的共享近鄰的定義來表征兩點間的局部密度，進而影響兩點間的相似度。共享近鄰的定義如下。

定義1數據集X={x1，x2，…，xn}中任意兩點xi和xj的共享近鄰定義為

SNN（xi，xj）=|n（xi）∩n（xj）|?? ，

其中n（xi）表示離點xi距離最近的前p個點，n（xj）表示離點xj距離最近的前p個點。一般地，參數p=20，本研究取數據集中樣本點數的5%。

2.3所提算法

譜聚類算法是依托譜圖劃分理論發展起來的，能在任意形狀的樣本空間上得到全局最優解。其主要核心是對特征向量的聚類，而特征向量是由樣本數據的相似矩陣特征分解得到的，構建一個性能優越的相似矩陣至關重要。本研究構建了一種自適應的相似矩陣，首先選用測地距離函數表征數據間的距離度量，相距較近的兩點間的距離近似于歐式度量，相距較遠的兩點間的距離則是通過最近鄰點間的歐式度量疊加得到的，這樣得到的距離度量克服了歐式距離的局限性，實際意義較明顯。然后根據每個點所處鄰域的稠密程度，用兩點間的共享近鄰數表征其密度，進而得到待聚類數據點的基于測地距離和共享近鄰數的相似度，構建對應的相似矩陣，對其特征分解后得到的特征向量進行聚類。算法流程如下。

輸入：待聚類數據集X={x1，x2，…，xn}，聚類個數k，共享近鄰數p;

1）根據2.1節計算數據集X={x1，x2，…，xn}中數據點之間的測地距離dG（xi，xj）;

2）根據定義1計算任意兩點xi和xj的前p個共同近鄰數SNN（xi，xj）;

3）計算基于測地距離和共享近鄰的數據點之間的相似度，構造相應的相似矩陣W=[wij]n×n，其中：

wij=exp（-d2G（xi，xj）σiσj（SNN（xi，xj）+1）），i≠j，1，i=j，

式中σi和σj分別表示點xi和xj到各自第l個近鄰的歐式距離，參見文獻[15]，建議l=7。

4）構建規范化Laplacian矩陣L=D-1/2WD-1/2，其中D=diag（d1， d2，…， di，…，dn），di=∑nj=1wij 。

5）計算矩陣L的前k個最大特征值及其對應的特征向量v1，v2，…，vk，可以得到特征矩陣V=[v1，v2，…，vk]∈Rn×k;

6）將矩陣V的行向量規范為單位向量，得到新矩陣為U，則uij=vij/（∑kv2ik）1/2;

7）將矩陣U的每一行對應回原數據集中的相應點，利用kmeans算法將其聚成k類C1，C2，…，Ck。

3實驗與分析

為了驗證本研究算法的性能，對比算法為k均值算法（kmeans）和基于規范化拉普拉斯矩陣的譜聚類算法（NJW），實驗數據集為5個人工數據集和5個真實UCI數據集。

實驗的操作平臺為64位win7系統、CPU為Intel（R） Core（TM）i52450M（2.50 GHz）、4G內存的計算機和Matlab R2014a。

3.1評價指標

對聚類結果的評價是檢驗聚類算法結果好壞的重要環節，不同的評價標準會突出聚類算法不同的特性。本研究選取Rand指標[16]作為評價標準，即根據本研究算法得到的決策數的正確率來評價算法的性能。定義決策數的正確率如下：

RI=a+da+b+c+d。

假設待聚類數據集有n個樣本，任意2個樣本可組成一個樣本對，則有n（n-1）/2個樣本對，即有n（n-1）/2個決策數目。式中：a表示同一類的樣本對被聚類到同一簇中;b表示不同類的樣本對被聚類到同一簇中;c表示同一類的樣本對被聚類到不同簇中;d表示不同類的樣本對被聚類到不同類的簇中，即a+d表示聚類正確的決策數，a+b+c+d表示總決策數n（n-1）/2。可知RI ∈（0，1），當RI的值越大，則說明決策數的正確率越高。當RI=1時，則說明聚類算法的聚類結果完全正確。

3.2數據集及實驗結果分析

3.2.1人工數據集

5個人工實驗二維數據集的詳細信息如下：

Twomoons數據集：由2個弧形結構構成，1 502個樣本，2個類。

LineBlobs數據集：笑臉形，包含266個樣本，3個類。

Spiral數據集：螺旋形，包含944個樣本，2個類。

Sticks數據集：由4個線形結構構成，包含512個樣本，4個類。

Threecircles數據集：由同心圓構成，包含299個樣本，3個類。

實驗結果在圖4中給出，本研究所提算法在密度分布不均和非塊狀（弧形、圓圈形、線形等）數據集上都得到最優劃分，證明了基于自適應相似度矩陣的譜聚類算法的強大聚類功能。而kmeans算法和NJW算法都或多或少的出現了不同程度的聚類錯誤。試驗中NJW算法中σ的取值為數據點距離差值Δd的10%～20%時較理想[17]（Δd=maxi≠j Dij-mini≠j Dij，這里的D為歐式距離矩陣），統一取σ=0.1Δd。

3.2.2標準UCI數據集

5個真實實驗數據集來自UCI數據庫，分別是：

鳶尾花數據集——Iris Data Set，后文簡稱Iris;

葡萄酒數據集——Wine Data Set，后文簡稱Wine;

玻璃鑒定數據集——Glass Identification Data Set，后文簡稱Glass;

澳大利亞信貸審批數據集——Statlog （Australian Credit Approval） Data Set，后文簡稱Acd;

鈔票驗證數據集——Banknote Authentication Data Set，后文簡稱Bna。

數據特征如表1所示。

表2給出的是k-means、NJW和本研究算法的聚類準確率，在NJW算法中的最后一步會用到k-means算法劃分，而在應用該算法時，不同的初始類中心會產生不同的聚類結果，為了降低此影響，本研究的k-means和NJW算法的取值都是程序運行20次的平均值。上節提到NJW算法中σ的取值為數據點距離差值的10%～20%較理想，不失一般性，取δ=0.1d和δ=0.2d兩種情況下進行驗證實驗。

從表2給出的準確率的對比分析可知，在Wine數據集和Bna數據集上的聚類效果k-means算法優于NJW算法，在Iris數據集和Acd數據集上的聚類結果，不論NJW算法取哪個參數都要比k-means算法高，而在Glass數據集上，k-means算法的聚類結果則介于NJW算法的2個不同參數得到的聚類準確率之間，這表明對具有不同結構的數據集，不同算法都有其優缺點。而本研究所提算法在這5個實際數據集上的聚類準確率都是最高的，再一次證明了本研究算法的魯棒性。

4結語

聚類結果對高斯核函數中尺度參數的選取極其敏感，距離函數在相似矩陣的構建中同樣占據至關重要的地位，沒有一種距離函數適合所有類型的數據集。本研究在充分分析數據聚類一致性特征的基礎上，選用測地距離函數表征數據間的距離度量，同時引入共享近鄰的定義來表征兩點間的局部密度，進而構建了一種自適應的相似矩陣，更好地刻畫數據集的本征結構，應用到譜聚類算法后，在密度分布不均以及非塊狀（弧形、圓圈形、線形等）的人工數據集上、通用國際UCI實際數據集上進行實驗，表明了本文算法對復雜分布數據有很強的自適應能力，且準確率較高。下一步的研究重心將放在運行效率的提高以及在高維數據集上的準確性研究方面。

參考文獻/References：

[1]楊英，李海萍，于向東，等.基于因子和聚類分析的中國各省市競爭力分析與研究[J].河北工業科技， 2013， 30（5）： 347-351.

YANG Ying，LI Haiping，YU Xiangdong，et al. Research of competitive power of provinces and cities in China based on factor analysis and cluster analysis[J]. Hebei Journal of Industrial Science and Technology， 2013， 30（5）： 347-351.

[2]LUXBURG U. A tutorial on spectral clustering[J]. Statistics and Computing， 2007，17（4）： 395-416.

[3]劉仲民， 李戰明， 李博皓，等. 基于稀疏矩陣的譜聚類圖像分割算法[J].吉林大學學報（工學版）， 2017， 47（4）：1308-1313.

LIU Zhongmin， LI Zhanming， LI Bohao，et al. Spectral clustering image segmentation algorithm based on sparse matrix[J]. Journal of Jilin University（Engineering and Technology Edition）， 2017， 47（4）：1308-1313.

[4]MIJANGOS V， SIERRA G， MONTES A. Sentence level matrix representation for document spectral clustering[J]. Pattern Recognition Letters， 2017， 85：29-34.

[5]RODRGUEZ-PULIDO F J， GORDILLO B， LOURDES GONZLEZ-MIRET M， et al. Analysis of food appearance properties by computer vision applying ellipsoids to colour data[J]. Computers & Electronics in Agriculture， 2013， 99（99）：108-115.

[6]孔萬增， 孫昌思核， 張建海，等. 近鄰自適應局部尺度的譜聚類算法[J]. 中國圖象圖形學報， 2012; 17（4）： 523-529.

KONG Wanzeng， SUNCHANG Sihe， ZHANG Jianhai，et al. Spectral clustering based on neighboring adaptive local scale[J]. Journal of Image and Graphics， 2012， 17（4）： 523-529.

[7]劉馨月， 李靜偉， 于紅，等. 基于共享近鄰的自適應譜聚類[J]. 小型微型計算機系統， 2011， 32（9）： 1876-1880.

LIU Xinyue， LI Jingwei， YU Hong，et al. Adaptive spectral clustering based on shared nearest neighbors[J]. Journal of Chinese Mini-Micro Computer Systems， 2011， 32（9）： 1876-1880.

[8]張亞平， 楊明. 一種基于密度敏感的自適應譜聚類算法[J]. 數學的實踐與認識， 2013， 43（20）： 150-156.

ZHANG Yaping， YANG Ming. A kind of density sensitive adaptive spectral clusting algorithm[J]. Mathematics in Practice and Theory， 2013， 43（20）： 150-156.

[9]INKAYA T. A parameter-free similarity graph for spectral clustering[J]. Expert Systems with Applications， 2015， 42（24）： 9489-9498.

[10]BEAUCHEMIN M. A density-based similarity matrix construction for spectral clustering[J]. Neurocomputing， 2015， 151（151）： 835-844.

[11]BROCKMANN D， HELBING D. The hidden geometry of complex， network-driven contagion phenomena[J]. Science， 2013， 342（6164）： 1337-1342.

[12]李方源. 基于電阻距離的中文文本譜聚類算法研究[D].廣州：華南理工大學， 2013.

LI Fangyuan. Study of Spectral Clustering for Chinese Document Base on Resistance Distance[D]. Guangzhou： South China University of Technology， 2013.

[13]TENENBAUM J B， de SILVA V， LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science， 2000， 290（5500）： 2319-2323.

[14]JARVIS R A， PATRICK E A. Clustering using a similarity measure based on shared nearest neighbors[J]. IEEE Transactions on Computers， 1973， 22（11）： 1025-1034.

[15]ZELNIK-MANOR L， PERONA P. Self-tuning spectral clustering[J]. In Proceeding of NIPS， 2005， 1601-1608.

[16]YEH C C， YANG M S. Evaluation measures for cluster ensembles based on a fuzzy generalized Rand index[J]. Applied Soft Computing， 2017， 57：225-234.

[17]ERTZ L， STEINBACH M， KUMAR V. A new shared nearest neighbor clustering algorithm and its applications[C]// Workshop on Clustering High Dimensional Data and Its Applications， at Siam International Conference on Data Mining.[S.l.]：[s.n.]， 2002， 105-115.