卷積神經網絡的方程組求解
周偉 陸玉穩
摘要:通過迭代求解方程組的解,提出了一種基于卷積神經網絡求解線性方程組的病態方程組的方法,由于條件數過大,影響求解的精度,將求解方程組的過程轉換為神經網絡學習的過程。通過神經網絡學習同目標數據形成一種映射關系,用最小化誤差來實現參數優化,把方程組求解的問題進而轉換成參數的優化問題,求得目標解。卷積神經網絡的參數共享機制在高維的矩陣計算中減小了計算量,提高了計算效率。
關鍵詞:卷積神經網絡;病態方程組;參數優化;線性方程組;條件數
中圖分類號:TP183文獻標志碼:A文章編號:1008-1739(2018)22-69-4
0引言
方程組的求解是科學與工程計算中的基本問題,在眾多的工程計算和控制領域,以及醫學領域有著廣泛的運用,眾多的算法提出也為問題的解決提供了較為有力的支持,例如預處理共軛梯度法、奇異值分解法、遺傳算法及BP算法等,但是傳統的方法仍存在一些問題,比如傳統的方法基本上都是建立在串行的基礎上進行,但是并行運算比較困難,而人工神經網絡可以提供一種并行計算的方法,卷積神經網絡的出現在一定程度上可以解決存在的問題。提出了基于誤差反向傳播的卷積神經網絡算法[1],以2層神經網絡對方程組進行求解來達到目的[2]。
1基于卷積神經網絡的方程組求解
1.1卷積神經網絡
卷積神經網絡是一種人工神經網絡,在眾多的領域被廣泛運用,例如圖像處理、視頻分析、目標追蹤、自然語言處理及人臉識別等,卷積神經網絡同傳統意義上的人工神經網絡有所區別,它采用了權重共享機制,通過權重共享機制大大減少了權重的數量,從而降低了計算過程中的復雜程度,卷積神經網絡的優良特性歸功于它的網絡結構,該網絡由輸入層、卷積層、池化層、全連接層和輸出層組成。
1.2卷積神經網絡模型
病態方程組的求解設計,充分地考慮了輸入與輸出的映射關系,該網絡具有以下特點:
①輸入與輸出:網絡結構接收來自系數矩陣的原始數據,并在不改變數據大小以及數量的前提下對系數矩陣的大小維度進行了重新定義。雖然未將系數矩陣的維度直接輸入,但是在計算系數矩陣維度時所耗時長可以忽略不計,輸出層的輸出就是經過卷積神經網絡的多次訓練后得到的預測的值與真實數據相近,而非真值[3]。
②線性映射:線性映射又叫線性變換,線性變換就是線性代數的一個研究的對象,在數學中,線性映射是在2個向量空間的函數,對于線性變化的討論可以借助矩陣來實現。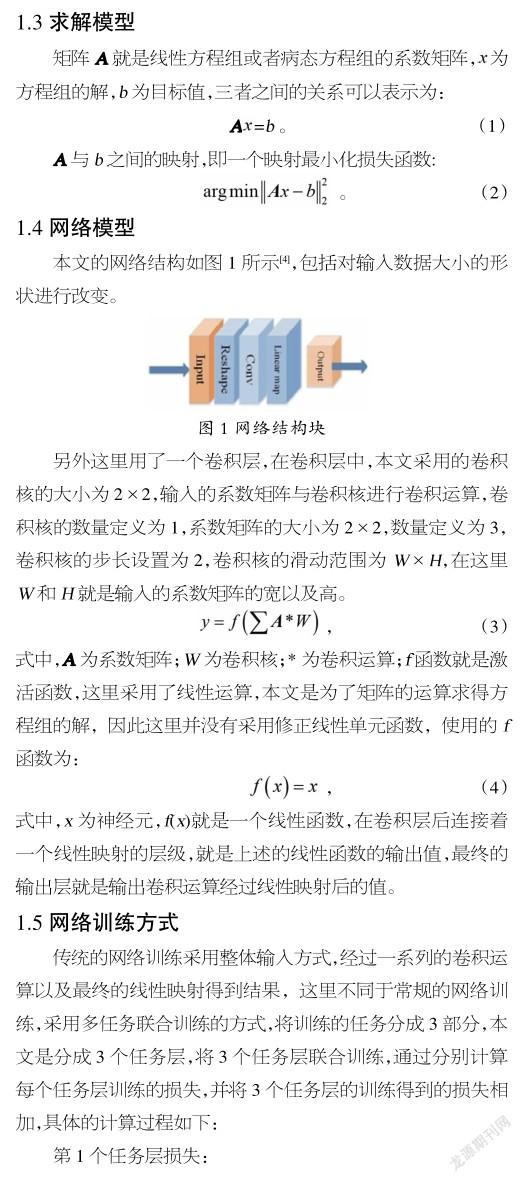
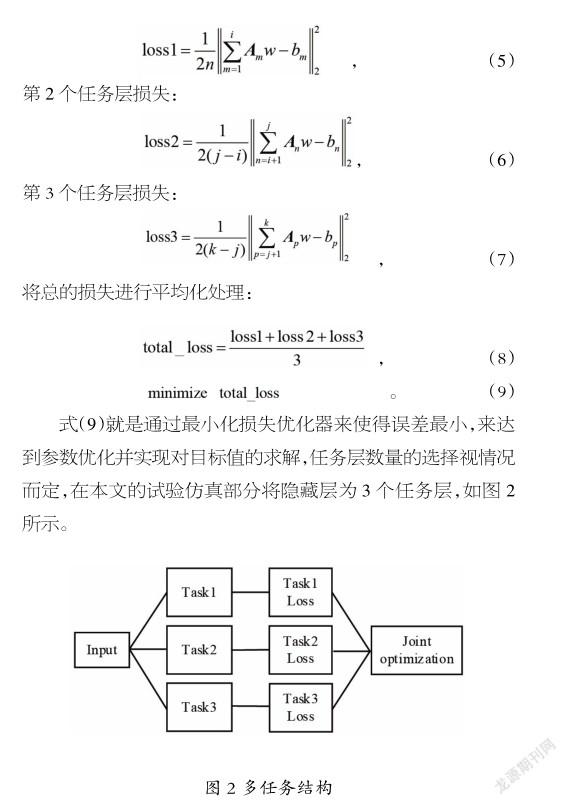
1.6參數的選擇與優化
(1)優化器的選擇
在Tensorflow中,存在著多種優化器可以選擇。①標準梯度下降法:匯集了樣本的總誤差,然后根據總誤差更新權值。②隨即梯度下降法:隨即抽取一個樣本的誤差然后更新權值,但是存在的問題可能會造成誤差增大。③批量梯度下降法,選取一個批次來更新權重,此外還有momentum,NAG,Adagrad,RMSprob,Adadelta及Adam等,這些優化器并不常用,在本文中選擇了Tensorflow這一框架,并且用Tensorflow提供的AdamOptimizer優化器,使用這一優化器來控制學習速度,會將之前衰減的梯度以及梯度的平方保存起來,使用RMSprob和Adadelta相似的方法更新參數。AdamOptimizer通過使用動量(參數的移動平均數)來改善傳統的梯度下降,促進超參數的動態調整,每次梯度調整后使得每次迭代學習率都有固定的范圍,使得參數較為平穩,為不同的參數計算提供不同的自適應學習率,適用于大多非凸優化問題。
而傳統的梯度下降存在較多的問題,比如容易造成梯度的消失等一系列的問題,不利于本文采用的神經網絡的訓練,因此在這里并未采用傳統的梯度下降法。
(2)學習率的選擇
傳統的學習率選擇都將會采用一個固定值,依據先驗知識,一定范圍內對數值進行取值,不斷實驗。根據訓練的結果好壞做參數調整,最終找到一個合適的學習率。在本文中學習率的選取并不是一個數值不變的常數,而且本文的學習率的選擇中是在每100次訓練后,對學習率進行動態調整,將學習率的取值在每100次后除以3,經過200次訓練,也就是對學習率進行2次調整,最終實現超參數最優,即權重最優。
(3)權重的選擇
權重的初始化對于神經網絡的訓練非常重要,如果權重一開始就很小,那么信號最后也會很小,如果權重很大,則信號也會變得很大,不合適的權值會使得隱藏層輸入方差過大,因此這里對權重的初始化選擇設置為符合正態分布的數值矩陣。
(4)正則化的約束

該方程的精確解為[1,-1],且系數矩陣條件數為2.1932×106,是一個典型的病態矩陣[5],求解的網絡結構同圖1的結構相似,定義了卷積核的大小為2×1,進行卷積計算。通過最小化卷積計算后的輸出與目標輸出的誤差,經過多次訓練迭代來優化權重直至找到適合網絡模型的權重,最終求解正確率比較精確,結果為[1.0373,-1.0518]T,該解與精確解在2-范數下的絕對誤差僅為2×10-3。在病態的方程組中求得最終解的準確率仍然較高,基本上達到預期結果。
3實驗結果
深度學習發展迅速,卷積神經網絡的運用及其廣泛,可以將卷積神經網絡與其他的領域相結合,比如醫學領域,不僅是在醫學圖像處理領域更是會在三維重構得到較好的運用,方程中的是帶有噪聲的,可以依據卷積神經網絡對噪聲進行過濾進而重構出想要的模型。
4結束語
針對傳統的線性方程組以及病態方程組的求解方法,采用了卷積神經網絡對方程組進行了求解,結合多任務聯合訓練的方式對方程組進行求解,從最終的結果來看,不論是對一般的方程組還是病態方程組都有較好的求解,準確率達到預期,且本文的網絡結構大大降低了計算的復雜度,卷積神經網絡在深度學習中有著較好的運用,在圖像處理、目標追蹤及人臉識別等眾多研究領域有著良好的運用,尤其是在特征提取運用很是廣泛,而且大大減少了計算的復雜程度和參數,因此卷積神經網絡的多功能性仍然值得繼續挖掘,運用在眾多的領域。
參考文獻
[1]周筍,吉國力.基于改進BP算法的廣義逆矩陣求解方法[J].廈門大學學報:自然科學版,2003(3):386-389.
[2]韓立群.人工神經網絡教程[M].北京:北京郵電大學出版社, 2006.
[3]李傳朋,秦品樂,張晉京.基于深度卷積神經網絡的圖像去噪研究[J].計算機工程,2017,43(3):253-260
[4]章云港,易本順,玥吳晨,等.基于卷積神經網絡的低劑量CT圖像去噪方法[J].光學學報,2018,38(4):123-129.
[5]李海濱,尚凡華.基于神經網絡的病態線性方程組求解[J].遼寧工程技術大學學報,2007(6):956-958.

