深度教學下有效促進生生互動的研究

黃志成

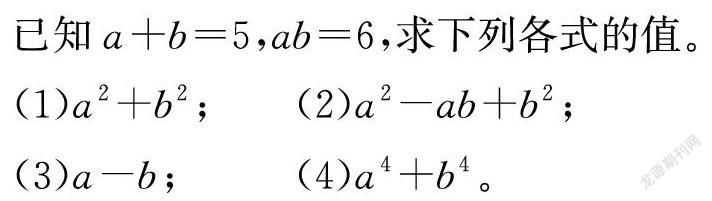
摘要：在多變的教學環境中，深度教學重視有效地促進生生互動，化形式為實質。本文主要從組內互助、組際競爭、組間互補三個方面進行探討，從而達到不斷提升學生能力的目的。

關鍵詞：深度教學?生生互動?組內互助?組際競爭?組間互補

課堂教學環境是復雜而多變的，作為課堂活動要素的老師和學生之間總是存在各種相互間的作用與影響。傳統課堂教學雖然也強調教師與學生的多邊互動，但是在教學的過程中仍偏重于教師的單邊活動，師生間的這種交流方式始終無法使得學生的思維得到全面的發散，受到了一定的局限，難以發揮出教學的全部價值。新課程改革的核心理念強調“一切為了每一位學生的發展”，因此有越來越多的教師開始在原有教學模式下增設并嘗試使用生生互動這一教學資源，不再僅限于師生互動，為課堂教學增色添彩。但真正實施到課堂中時，我們仍能發現存在不足，比如生生互動更多的是偏重于形式化，走流程，缺少真正實現生生互動的教學資源支持，特別是對生生互動的價值沒有足夠的認識，在很大程度上對運用生生互動這一教學資源促進學生達到全面且均衡發展產生了影響。在此條件下，深度教學將充分挖掘以往課堂中所容易忽視的教學資源條件，將學生引向深度學習，卷到學習的浪潮中來，才能加強生生互動，化形式為實質，提高教學效能，對于推動新課程改革具有重要價值。本文將從“組內互助，團結協作”“組際競爭，力爭上游”“組間互補，共同進步”三個方面論述在深度教學下如何有效促進生生互動。

一、組內互助，團結協作

《禮記·學記》指出：“獨學而無友，則孤陋而寡聞。”如今的學生中獨生子女所占比例很大，缺乏人際交往與相處，合作意識比較淡薄。本校在深度教學理論基礎上將班級學生從成績、性格、興趣、愛好等方面分組，全面考慮學生能力和特質，兩兩結對兵教兵，多以四人編組，把班里所有學生按標準分到水平均衡的學習互助小組內，共同將好的經驗組內分享，意在通過生生互動讓學生學習的活力得到激發，營造充滿生命力的課堂。但我們要注意的是，同學合作不是為了一幫一，而是小組內所有同學間的互助、互惠、互贏！

案例1：用代入法解下列方程組：

x+2y=2?①x-2y=4?②

是否可以不用代入法解出方程？

（讓學生思考，小組內同伴相互交流，小組代表發言。 ）

思考：1.相同未知數的系數有何特點？

2.不用代入法是否也可以消元？如果可以，有幾種方法？

發現：①+② 可消去x;

①+② 可消去y。

總結：解方程組始終要圍繞“消元思想”進行，觀察上面的方程組不難發現，可將方程①和方程②的兩邊分別進行相加得到2x=6或者相減得到4y=-2，就可以消去一個元，直接得到易解的一元一次方程，解出未消去的元，就可以再往回代入解出消去的元，得出方程組的解。當我們發現方程組中兩個二元一次方程存在一個元的系數互為相反數或系數相等的時候，就可以將兩個方程的兩邊分別相加或者相減，消去這個未知數，得到一個一元一次方程，稱這種方法為加減消元法。

在本題中，小組內能夠解決的問題，同學可以互相交流自己的想法，會的同學可以將自己的方法教給不會的同學，得出小組內同學共同認可的答案，讓小組代表答出本小組的觀點，相互進步。

學習好的同學在將自己的想法講給別的同學聽時，不單單是付出，更多的是收獲。當你把別人不懂的問題給別人講明白時，你不僅有一種成就感，更有一個難得的檢驗自己的機會。與你搭檔的伙伴實際上是你應該感謝的“傾聽者”，別人認真地傾聽你的解答也是在給你搭建展示的舞臺。你在給別人講解的過程中不但把已有知識記得更牢固，而且思路更清晰，口才更流利，表達能力更強，幫人改正錯誤等于幫自己防范錯誤，利人利己。一個問題自己能看明白不算是真正地理解，只有給別人講明白了才算真正地達到了目的，努力讓每位同學都能“學進去，講出來”。想讓組內互助發揮出最佳效果，充滿學習動力，就需要制定有效的評價模式，讓組與組之間一較高下。

二、組際競爭，力爭上游

小組之間開展競爭學習時，同等學力的小組自然不甘示弱，小組內同學興趣愛好各不相同、各有所長就發揮了極大的作用，每位同學都懷揣著對自己小組的歸屬感和認同感，背負著小組的共同利益，都想為自己的小組爭得榮譽，滿足自身的成就需要。在滿足成就需要的驅使下，小組間成員會變得更加默契，合作無間。當然，能夠達成高效率的小組內成員合作離不開教師正確的引領，所以實際教學過程當中，教師需要對每個教學環節精益求精，充分地調動學生的積極性，點燃學生心中的勝負欲，善于使用各種激勵措施，外部激勵在做出教學評價時不可或缺，一個小小的獎勵可以達到“四兩撥千斤”的效果，所以教師根據教學需要靈活性、創造性地使用競爭機制，充分調動學生的積極性，優化課堂教學效果。

案例2：利用乘法公式求下列代數式的值。

（教師激勵措施：先把四個題目全做對的小組得到積分獎勵。）

已知a+b=5，ab=6，求下列各式的值。

前兩個小題對于牢固掌握了完全平方公式的同學來說很簡單;第三小題容易在對（a-b）2開平方時，遺漏答案;第四小題則難度有所提升，學生難以通過題干已知條件轉化到a4+b4，同時也要借助于第一問中的a2+b2對其平方，再進行轉化或者通過題干和第三小題直接解出a、b，也可以解出答案。想要完全把四道題目做正確，需要小組內組員的精誠合作，以最快的速度解決問題。在關乎小組榮譽時，組與組之間的競爭意識迅速增長，能積極有效地讓每位學生都投入到解題中來。

平時教學中也是如此，當教師拋出具有爭議性或挑戰性的問題時，各組的熱情都很高，每組組長要在參與討論的同時，為本組組員分配任務，記錄討論結果，保證活動有序進行，各小組成員要進行自主探究，動腦思考、查閱資料并進行組內合作交流，在自己的努力和團隊的協作之下解決問題，獲取新知并享受到合作的快樂。這樣不僅可以最大程度地提高學生的學習趣味和學習的積極性，而且能提高學生的學習效率，收到更好的學習效果。

三、組間互補，共同進步

教育的理念始終是為了每一位學生的發展，雖然把班級分為一個個的小組，但最終還是為了讓每一位學生都能夠成人成才。人與人的特質不同，組與組也是一樣，任何時候都要群策群力才能收到最好的效果。深度教學下同學們的單一學習轉化為教學的多邊互助，小組合作互補學習，班里每位學生都得到了平等交流的機會，注重學生參與和學生知識形成的過程，聽明白，想明白，說明白。所有人互幫互助，互通有無，共同進步。小組與小組之間既要有競爭，也要有合作，互相之間取長補短，才能更好地進步，獲得全面且均衡的發展。

案例3：小明、小亮兩人約好同時從相距2.4千米的兩地相向而行，小明步行出發每分鐘可走80米，小亮騎自行車出發，8分鐘后兩人相遇。小亮騎自行車每分鐘行多少米？（盡量思考多種方法）

思路1：單位不一致，先進行單位換算：2.4千米=2400米（以下思路均是）。先求出小明總共走了多少米，然后用總路程減去小明走的路程，得到小亮騎自行車所行的路程，再用路程÷時間得出小亮騎自行車的速度。

解法1：小明走的路程?80×8=640（米）

小亮騎自行車的路程?2400-640=1760（米）

小亮騎自行車的速度?1760÷8=220（米/分鐘）

綜合算式：（2400-80×8）÷8=（2400-640）÷8=1760÷8=220（米/分鐘） 。

思路2：先用兩地總路程÷總時間，可以得到小明和小亮的速度之和，用兩人的速度之和減去小明步行的速度，就可以得出小亮騎自行車的速度。

解法2：小明和小亮速度之和?2400÷8=300（米/分鐘）

小亮騎自行車的速度?300-80=220（米/分鐘）

綜合算式：?2400÷8-80=300-80=220（米/分鐘）

思路3：由題意得出等量關系“小明和小亮的速度之和×相遇所用時間=兩地間總路程”，列一元一次方程解決。

解法3：設小亮騎自行車每分鐘行x米。

（80+x）×8=2400

80+x=2400÷8

x=2400÷8-80

思路4：由題意得出等量關系“小明步行路程+小亮騎自行車行駛路程=兩地間總路程”，列一元一次方程解決。

解法4：設小亮騎自行車每分鐘行x米。

80×8+8x=2400

8x=2400-80×8

8x=1760

x=220

本題可以通過算術的方法與列方程的方法解決，并且方法多種多樣，一個小組得出的解法不全面，由其他小組繼續補充，發散所有小組內同學的思維，集思廣益，讓所有同學掌握解決同一數學題的多種方法，分析解法的優劣，找到適合自己最優的方法，加強分析、解題的能力，對于提高成績有著很大的益處。

深度教學下的生生互動，讓每一位同學都能夠有機會成為一名小老師，同學之間學會了互相督促和進步，更容易去發現同學在學習過程所存在的問題，也更容易讓學生來糾正學生的問題。要讓不會的同學主動地去問會的同學要主動去把不會的同學教會，由點帶面，你追我趕，從班主任掌控全班學生向學生相互監督學生、相互要求進步、主動管理自己轉變。班主任可以真正起到并且只需要起到引導者的作用，學生才能真正在教育的雙邊活動中占據主體地位，認識到學習是自己的首要任務，學生也在互助互動的過程中不斷地提高自己明辨是非、自我教育的能力，真正地讓自己得到全面且均衡的發展。

參考文獻：

[1]吳仁英.合作學習中的生生互動研究[D].濟南：山東師范大學， 2005.

[2]于春燕.引入小組競爭評價機制?打造小學英語高效課堂[J]. 新課程（小學）， 2014（5）：164-165.