單側揭露后側受壓膠結充填體穩定性分析
王瑞鵬 金愛兵 吳振坤 高永濤 張 金
(1.北京科技大學土木與環境工程學院,北京100083;2.金屬礦山高效開采與安全教育部重點實驗室,北京100083;3.山東金鼎礦業有限責任公司,山東淄博255000)
目前國內地下金屬礦山開采大多向安全、高效和清潔方向發展。階段空場嗣后充填采礦法以礦石回采效率高、貧化率低、有效改善采場地壓和充分利用尾礦等頗多優勢,在國內外金屬礦山被廣泛地推廣使用。在實際回采二步驟礦柱時,一步驟采場充填體的臨空區側處于豎向暴露狀態,另一側會受到非膠結充填體的側壓作用,充當“人工礦柱”的作用,以改善二步驟采場地壓,因此,保證一步驟采場膠結充填體的穩定性是階段空場嗣后充填采礦法順利實施的關鍵[1]。
針對單側暴露狀態下充填體強度合理確定問題,國內外學者主要采用的方法有解析方法、工程類比法、數值模擬和現場監測。加拿大Mitchell等[2]根據物理模型試驗中不同尺寸和強度的單側豎向揭露膠結充填體的穩定情況,歸納提出了一種基于極限平衡法的解析計算模型;Li[3]在經典解析方法(1982)的基礎上,考慮了充填成拱作用,得出了不同高寬比充填體的廣義修正Mitchell法;王 等[4]根據礦山實際膠結充填體力學參數,利用數值模擬得出不同回采順序開采時采場圍巖的應力和位移變化規律;于世波等[5]通過現場實時監測和數值模擬相結合,研究了充填體與圍巖變形之間的時空變化規律,構建了覆巖移動控制的三維力學模型;曹帥等[6]采用二維平面應變理論,通過半逆解法求解側壓作用下膠結充填體礦柱應力,并揭露采場寬度和高度對水平應力和剪應力影響規律,但其并未考慮圍巖與充填體之間的摩擦作用。已有的研究成果在一定程度上優化了充填體的強度設計,但存在一定缺陷,在非膠結充填體的側壓作用下的單側臨空充填體穩定性判斷方面研究成果極少。本研究充分考慮圍巖與充填體之間的摩擦作用,建立膠結充填體在側壓作用下的三維力學模型,探究充填體穩定性與后側非膠結體受壓作用、自身尺寸、充填體與圍巖之間有效摩擦力和頂部荷載之間關系。
1 充填體與圍巖之間相互作用
1.1 接觸面影響
充填體在地下采礦過程中發揮“人工礦柱”的作用,防止采場頂板的塌落和改善地壓,為采礦活動提供安全作業環境。充填體對圍巖所發揮的作用主要表現為支撐作用、阻止圍巖變形、吸收和轉移圍巖應力。在實際的采礦工程中,由于受到采礦爆破活動和節理交錯發育等因素的影響,暴露出的巖壁面絕大多數均為粗糙不規則。充填體與圍巖之間接觸面的粗糙程度直接影響充填體內部的應力分布。
1.2 側壓作用
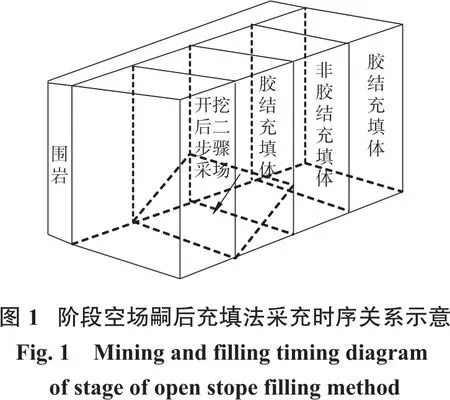
實際采充時序過程中,一步驟充填體一側的二步驟礦柱回采完畢后進行非膠結充填,隨后回采一步驟充填體的另一側相鄰二步驟礦柱,詳細的采充時序關系如圖1所示。此時,單側暴露膠結充填體后壁在非膠結充填體的側壓作用下產生呈線性分布的水平推力,進而影響膠結充填體穩定性[7-9]。因此,單側暴露充填體的穩定性僅考慮充填體自穩能力是不足的,充填體與圍巖之間產生的摩擦和非膠結充填體的側壓作用也是決定性因素。
2 膠結充填體力學模型分析
2.1 假設條件和力學模型
依據極限平衡理論和安全系數確定充填體強度方法在實際工程中是具有指導性意義的[10-12]。假設二步驟采場非膠結充填體的側壓力與充填體埋深成正比例關系,其中,γ2(kN/m3)視為比例系數,即非膠結充填體的容重,此為最保守的受力狀態;充填體與采場頂板接觸較為理想,且整個采充時序過程中各個工序較為及時。
根據經典Mitchell解析法中單側揭露膠結充填體的滑動破壞模式,在考慮后側非膠結充填體的側壓力作用下,充填體與圍巖之間產生的剪切力方向可能發生改變[12-16],設其方向與水平面夾角為β,膠結充填體的長度、高度和寬度分別以L、H、B表示,膠結充填體底部潛在滑移面與水平面之間夾角為α,則前壁揭露—后壁受壓條件下膠結充填體三維力學模型如圖2所示。
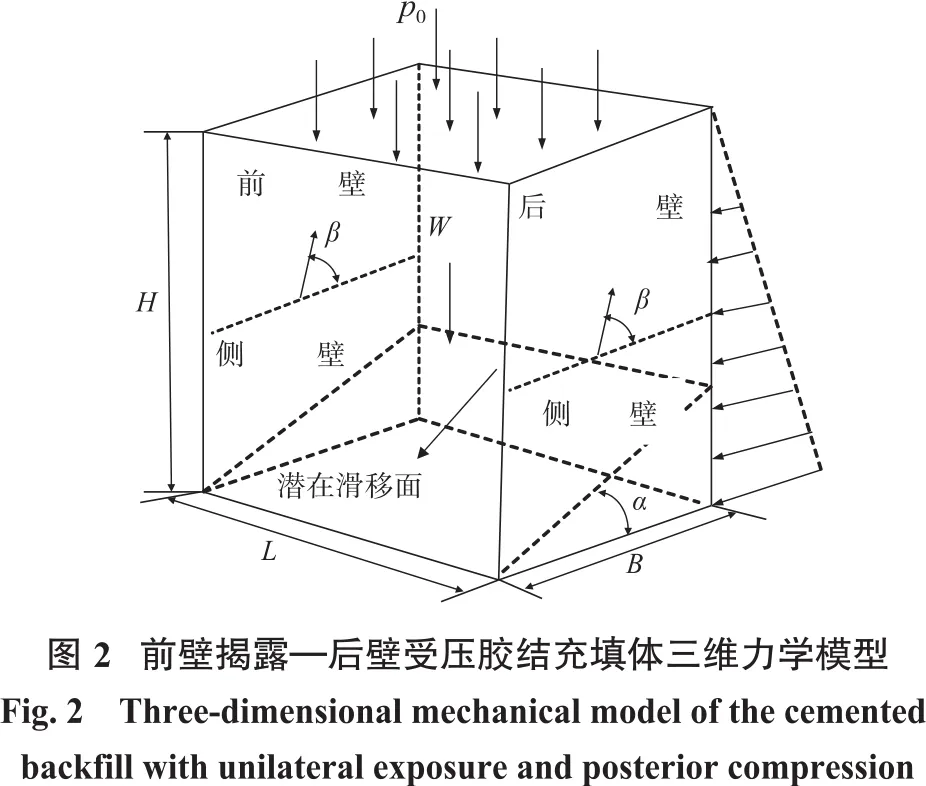
2.2 膠結充填體穩定性解析推導
設一步采膠結充填體容重為γ1,二步采非膠結充填體容重為γ2,膠結充填體后壁受到側壓作用力為p1,膠結充填體上端部所受豎向荷載為p0,膠結充填體與圍巖接觸面之間剪切力方向與水平方向夾角為β(由于膠結充填體后壁受側壓作用,剪切力方向可能發生改變,不再為豎直方向),根據文獻[12]研究,β取值為45°-0.5?。
膠結充填體楔形滑動體自重可表示為

式中,H*表示充填體楔形滑動體的有效高度,可根據下式計算:
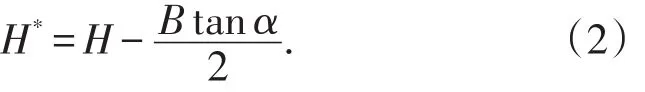
一步驟采場充填體埋深h處垂直于膠結充填體與圍巖接觸面的水平正應力大小[17]為
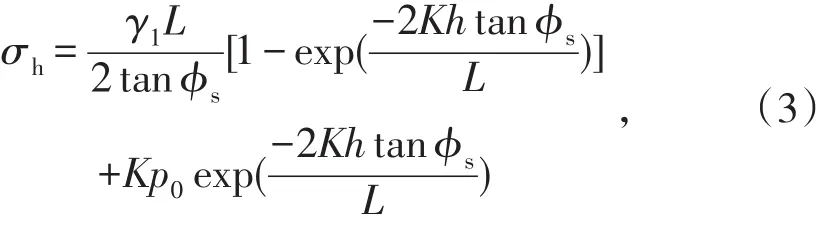
式中,K為側向壓力系數,可根據下式計算:
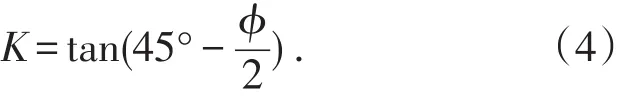
膠結充填體與圍巖接觸面之間剪切應力服從庫倫準則:
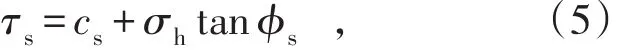
式中,cs為膠結充填體和圍巖接觸面之間的黏聚力;?s為膠結充填體和圍巖接觸面之間的內摩擦角,具體取值可根據下式計算:

式中,c為膠結充填體黏聚力;?為膠結充填體內摩擦角;rs為折減系數,取值范圍為0.25~1.0,本文取0.4;ri為折減系數,取值范圍為0.6~1.0,本文取1[12]。
膠結充填體與圍巖接觸面之間剪切力為
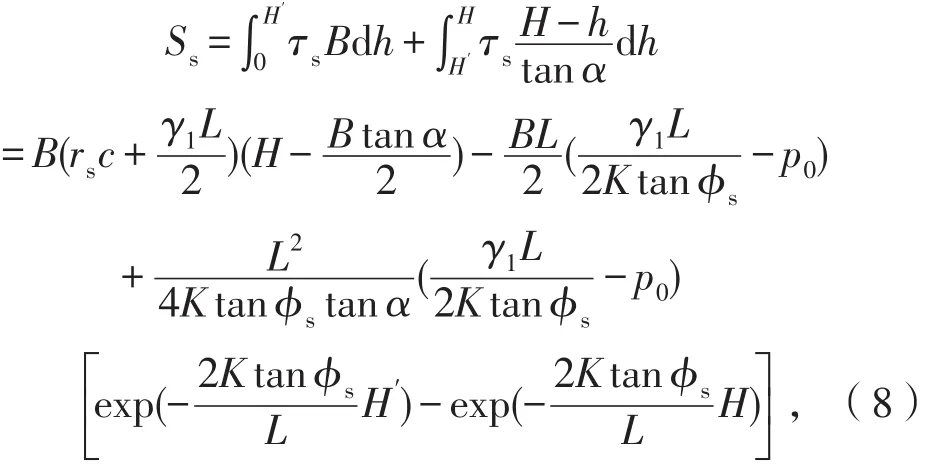
式中,H′=H-Btanα。
膠結充填體豎向合力為

膠結充填體產生的側壓作用力為
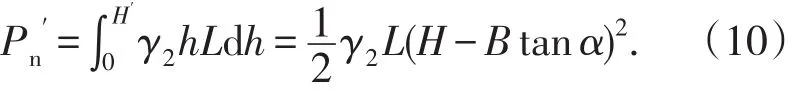
膠結充填體水平方向合力為
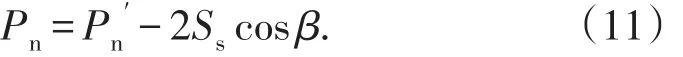
根據極限平衡力學理論,膠結充填體楔形滑動體的安全系數為
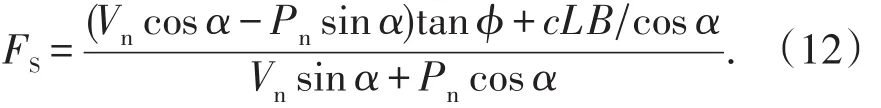
3 工程算例分析
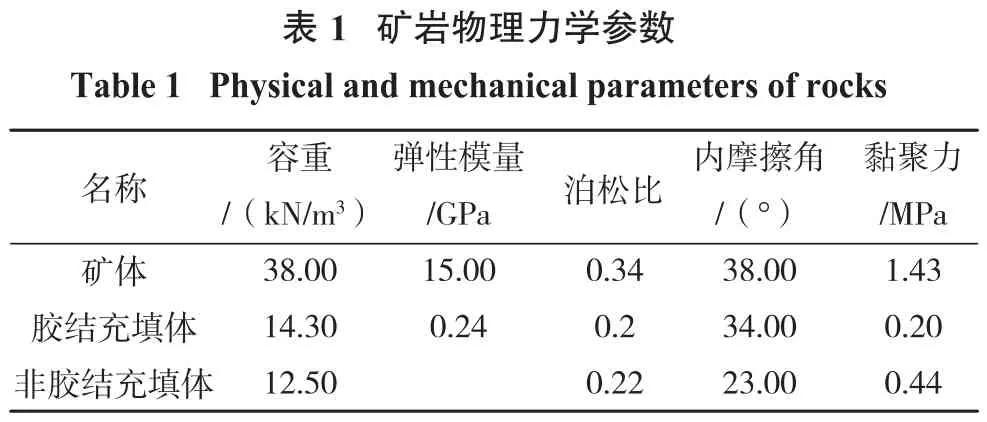
山東王旺莊鐵礦主要采用階段空場嗣后充填法,中深孔爆破方式進行落礦開采,礦體埋藏深度范圍為310~530 m,分4個中段水平進行開采,年產量現已達到250萬t,礦石品位高,圍巖堅固性較強,隨著一步采礦柱逐漸減小,目前正處于二步驟采礦試驗階段。礦體、膠結充填體和非膠結充填體的物理力學參數見表1。
?
3.1 安全系數分析
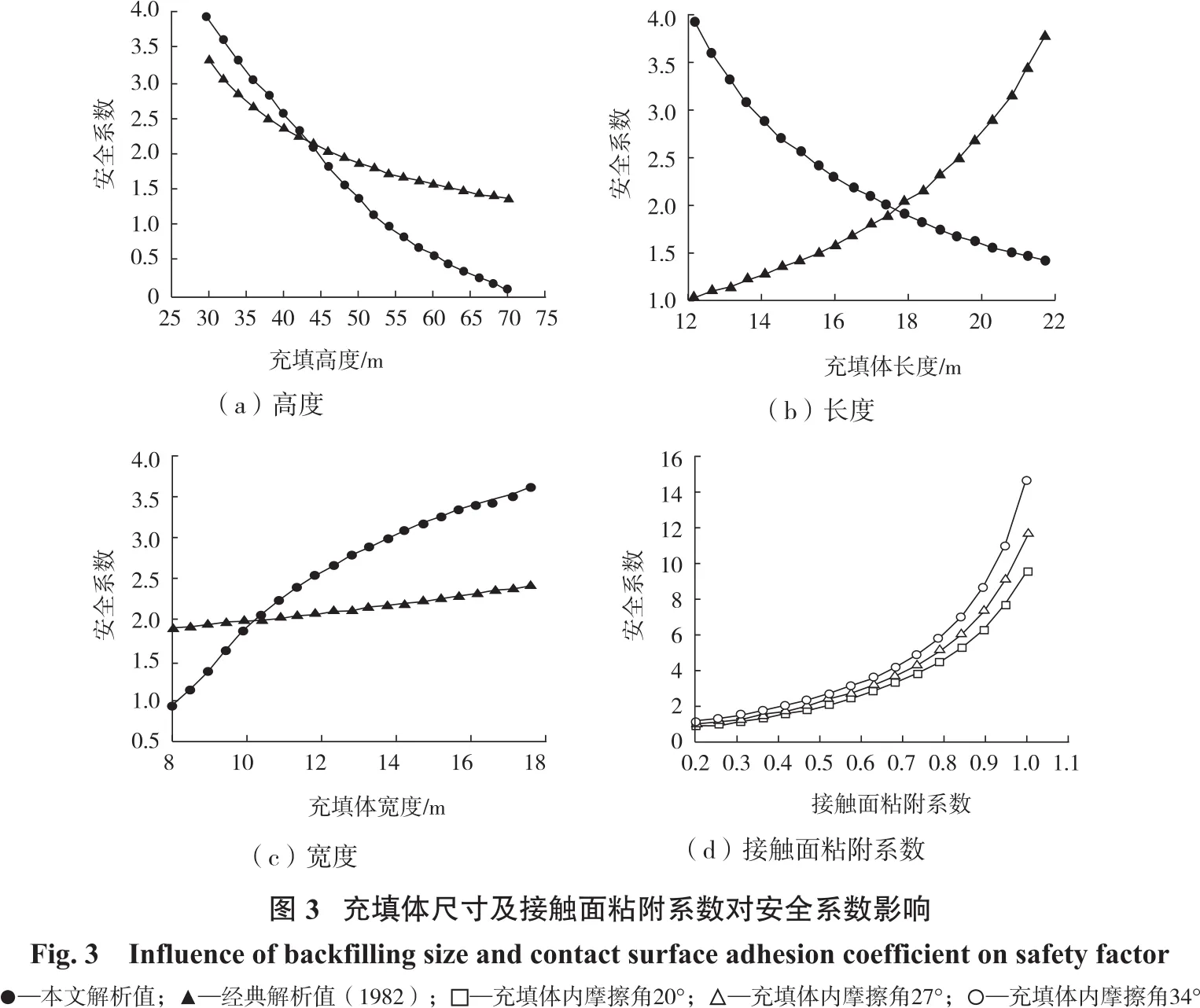
一步驟采場膠結充填體尺寸以及圍巖與充填體接觸面粘附系數對充填體安全系數的影響分布規律如圖3所示。
觀察圖3(a)發現,充填體的安全系數與充填體高度呈負相關,且本文解析值與經典Mitchell解析值(1982)呈現的趨勢相同;充填體高度為70 m,前者安全系數值接近于0,后者安全系數為1.36;前者曲線斜率絕對值較后者大,下降較為明顯。這也表明經典Mitchell法在充填體穩定時所需的大黏聚力存在局限性。
觀察圖3(b)發現,充填體的安全系數(本文解)與充填體長度呈負相關,而經典解結果與之相反,原因是經典解并未考慮后側受壓因素和圍巖與充填體接觸面產生的水平摩擦力因素。充填體長度小于17.7 m,前者安全系數大于后者,充填體長度大于17.7 m,前者安全系數小于后者,原因是充填體后側壓產生的水平推力(長度大于17.7 m)大于圍巖與充填體接觸面產生的水平摩擦力,降低充填體穩定性。
觀察圖3(c)發現,充填體的安全系數與充填體寬度呈正相關,且本文解析值與經典Mitchell解析值(1982)呈現的趨勢相同;充填體寬度小于10.4 m,前者安全系數小于后者,充填體寬度大于10.4 m,前者安全系數大于后者,原因是充填體后側壓產生的水平推力(長度大于10.4 m)小于圍巖與充填體接觸面產生的水平摩擦力,增強充填體穩定性。
觀察圖3(d)發現,充填體的安全系數隨圍巖與充填體接觸面粘附系數增大而增大;充填體的安全系數隨內摩擦角的增大而增大,原因是接觸面粘附系數越大,圍巖與充填體之間的有效摩擦力越大,即增強了充填體穩定性。
3.2 黏聚力分析
一步驟采場膠結充填體尺寸以及圍巖與充填體接觸面粘附系數對充填體所需內聚力(FS=1)影響分布規律如圖4所示。
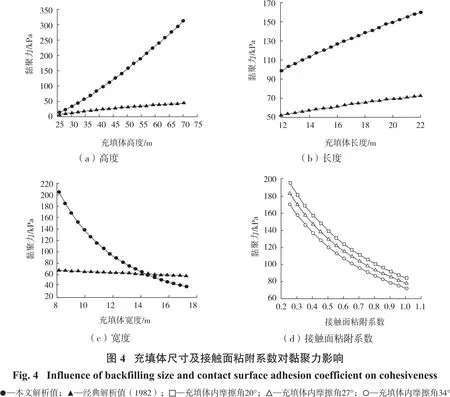
觀察圖4(a)~(c)發現,本文解中充填體高度、長度、寬度因素對充填體所需黏聚力(FS=1)產生的影響呈現的趨勢與經典法均相似;在圖4(a)、(b)中前者充填體所需黏聚力(FS=1)均大于后者,原因是充填體后側受壓因素存在;充填體寬度大于14.8 m時,前者充填體所需黏聚力(FS=1)均小于后者,原因是圍巖與充填體接觸面產生的摩擦力效應大于后側壓效應,即增強了充填體的穩定性。
觀察圖4(d)發現,充填體所需內聚力(FS=1)隨圍巖與充填體接觸面粘附系數和內摩擦角增大而減小,原因是接觸面粘附系數越大,圍巖與充填體之間的有效摩擦力越大,減弱了充填體發生滑移模式破壞。
3.3 頂部外荷載分析
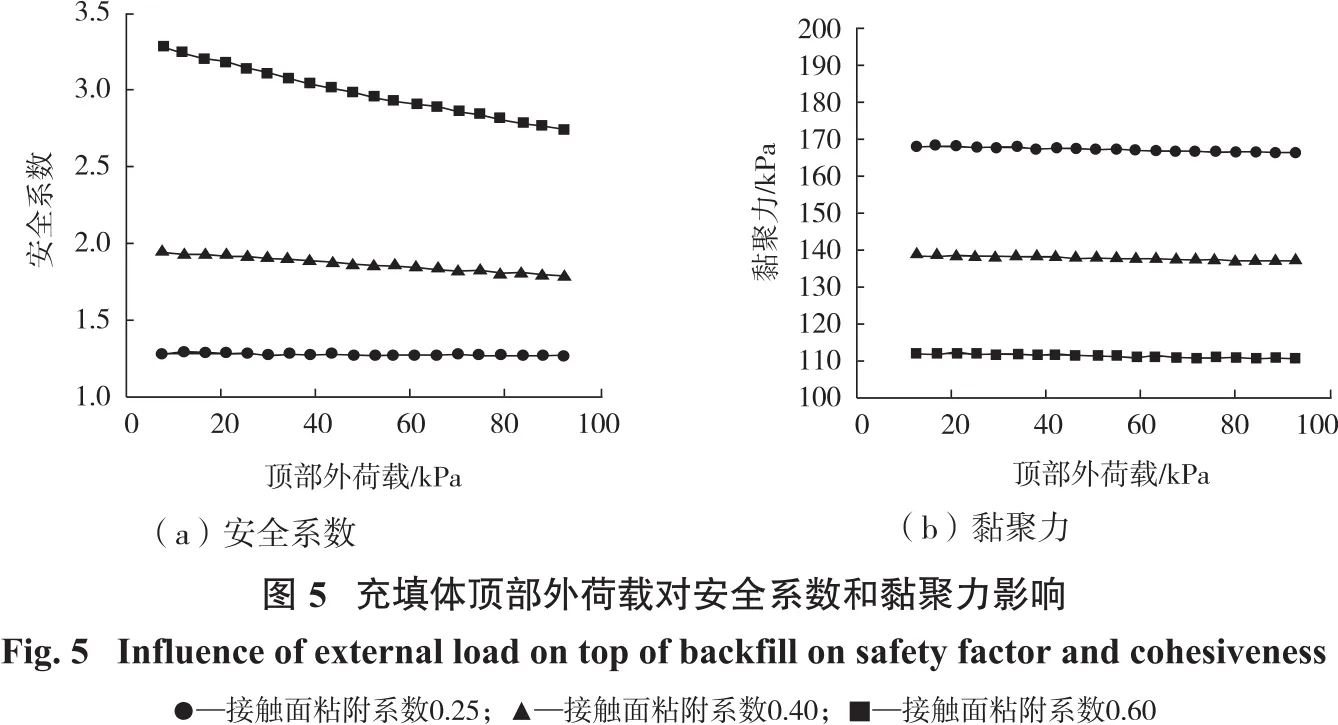
一步驟采場膠結充填體上部表面所受外荷載大小對充填體安全系數和所需黏聚力(FS=1)影響分布規律如圖5所示。
觀察圖5發現,充填體安全系數和所需黏聚力(FS=1)隨頂部外荷載增大幾乎呈線性減小,其中,安全系數隨頂部外荷載因素變化(接觸面粘附系數為0.6)的曲線斜率絕對值較大,因此,應當考慮膠結充填體上表面所受到的外荷載(可能來源于上部覆巖、采礦活動所需的機械設備以及后期新充填料的料漿等)影響。
4 結論
(1)在空場嗣后充填法中,根據采充時序過程中膠結充填體、圍巖和非膠結充填體三者之間力學作用關系,建立了更加符合現場實際的膠結充填體單側揭露后側受壓狀態下的三維力學模型,克服了經典法求解充填體穩定時所需的大黏聚力的局限性。
(2)充填體暴露面長度是充填體保持穩定的主導性因素;充填體的穩定性隨頂部外荷載增大而降低,同時隨膠結充填體內摩擦角的增大而增強。
(3)膠結充填體在后側受壓狀態下,設計充填體強度僅視為自立性人工礦柱模型是不足的,應當考慮后側非膠結體受壓作用、自身尺寸、充填體與圍巖之間有效摩擦力和頂部外荷載。
(4)探討了接觸面粘附系數對后側受壓膠結充填體安全系數和所需黏聚力的變化規律,該比例系數仍需后續更多試驗測試進行深入研究。

