針對特定輻射源識別的高精度符號同步方法

潘一葦，彭華，李天昀，王文雅

?

針對特定輻射源識別的高精度符號同步方法

潘一葦，彭華，李天昀，王文雅

（信息工程大學信息系統工程學院，河南 鄭州 450001）

對于特定輻射源識別的預處理環節，現有符號同步方法存在時延估計方式不妥和插值計算精度不足的問題。針對該問題，提出一種高精度的符號同步方法。對于時延估計，采用2步估計的方式，先由前向算法得到粗估計值，再利用解調得到的發送符號通過局部搜索得到精確值。對于插值計算，利用窗化法對插值濾波器進行優化設計，改善了濾波器的抗混疊特性，提高了計算精度。仿真實驗表明，與常規符號同步算法相比，該算法能有效解決以上問題，且能在輻射源識別中取得更優的識別效果。

特定輻射源識別；高精度；符號同步；時延估計；插值濾波器

1 引言

特定輻射源識別（SEI, specific emitter identification），即通過提取射頻信號上能夠體現輻射源個體差異的細微特征，實現對目標個體的識別。由于射頻指紋（RFF, radio frequency fingerprinting）特征不依賴通信內容，且難以偽造，因而在無線網絡安全和通信偵察對抗等民用和軍事領域均具有重要的應用價值。

SEI的本質是模式識別的問題：接收信號經過預處理后，先提取細微特征，再根據先驗信息完成分類識別，其中，特征提取是問題的核心。現階段，利用積分雙譜[1]、分形理論[2]和時頻分析[3-4]等方法直接對接收信號進行特征提取，所提特征容易受到調制信息的影響。為了克服該影響，Brik等[5]提出無源輻射裝置識別系統（PARADIS, passive radiometric device identification system），從解調所得的星座點上提取6種調制域特征，對138個無線設備的識別率超過了80%；文獻[6]將機器學習引入星座誤差的特征提取，改善了識別效果；文獻[7]推導并分析了I/Q不平衡失真條件下的基帶信號模型，利用幾何分析的方法提取RFF特征；黃淵凌等[8]建立了描述發射機相位噪聲特性的自回歸滑動平均（ARMA, auto-regressive and moving average）模型，通過估計ARMA參數構建特征，從而完成了個體識別。文獻[5-8]均是采用先解調再處理的方式，將特征提取的對象轉化為解調所得的星座點，然后將解調獲得的發送符號作為先驗信息，通過對比解調所得的星座點與理想星座點的差異，實現細微特征的提取，有效避免了調制信息的干擾。然而，由于對預處理環節的忽視，這類方法直接采用常規的解調算法，有些算法并不滿足SEI力求精細準確的要求，在預處理環節人為地引入了不必要的誤差，從而影響特征提取和分類識別的效果。

本文針對預處理環節中的符號同步，首先指出將現有方法直接應用于SEI的預處理環節會面臨時延估計方式不妥和插值計算精度不足的問題。對于時延估計，本文采用2步估計的方式，先由前向算法得到粗估計值，再以解調獲得的發送符號為輔助通過局部搜索得到精確值。對于插值計算，本文在詳細分析插值模型的基礎上，對插值濾波器進行優化設計并靈活地增加抽頭個數。仿真實驗表明，本文算法能夠有效解決上述2個問題，且能在SEI應用中取得更優的識別效果。

2 現有符號同步方法存在的問題

全數字符號同步可以分為時延估計和插值校正這2個部分。盡管關于符號同步的研究已經相當成熟，但將現有方法直接應用于SEI的預處理環節仍會面臨以下2個問題。

1) 時延的估計方式不妥

時延估計的方法主要分為前向和反饋2類。前者容易受到符號速率估計準確度和發射電路晶振穩定度的影響，估計誤差較大；后者存在hang-up現象，同步速度較慢。在實際應用中，我們通常采用前向與反饋相結合的方式進行符號同步，然而這種方式并不適用于通信輻射源的細微特征提取。這是因為：反饋結構會自適應調整時延參數，解調所得的星座點將趨于標準化，這就抹除了不同個體之間的細微差異，影響了識別的效果。

2) 插值的計算精度不足

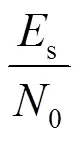
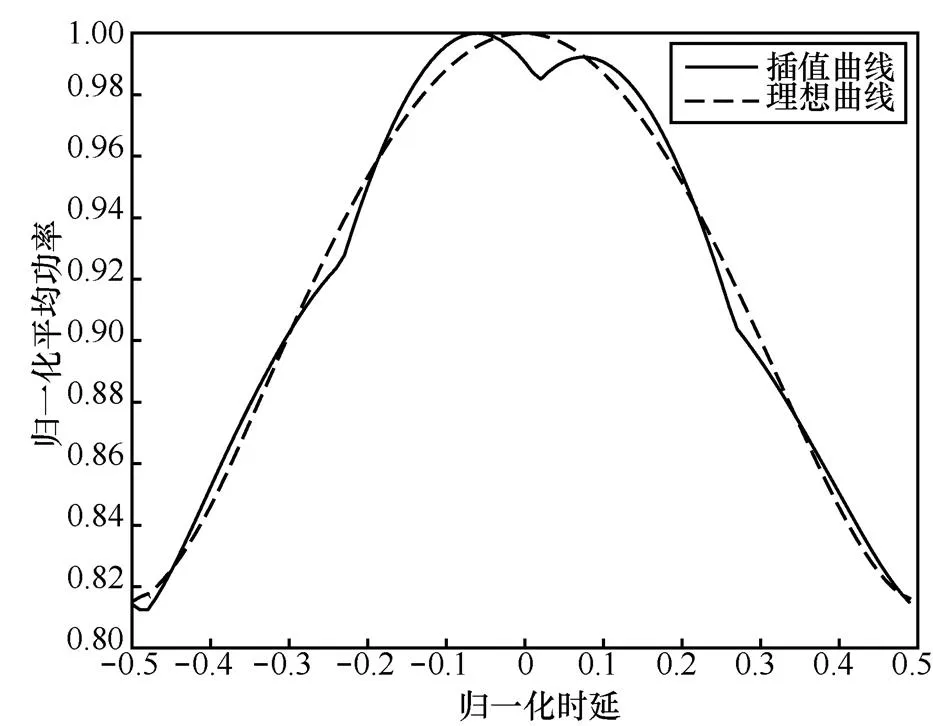
圖1 分段拋物線插值造成的失真

3 改進算法

設頻偏、相偏均為0，則經過匹配濾波后的基帶復信號可以表示為

由于反饋結構會影響識別效果，本文算法采用前向結構。現有的前向方法均采用盲估計的方式，即使在部分發送符號已知的情況下，只要能夠實現解調，便不會苛求時延估計的精度。然而對于SEI，所關注的并非信號解調，而是不同個體之間的細微差異。考慮到信號的信噪比普遍較高，可以近乎無誤碼解調，因此，為了更準確地提取細微特征，本文算法利用解調獲得的發送符號提高時延的估計精度是必要且可行的。

文獻[10]給出了數據輔助的時延估計準則，即

3.1 優化插值算法

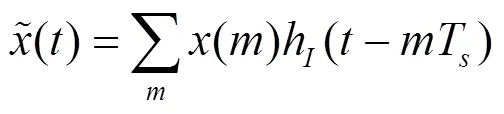
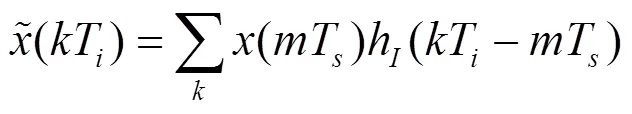
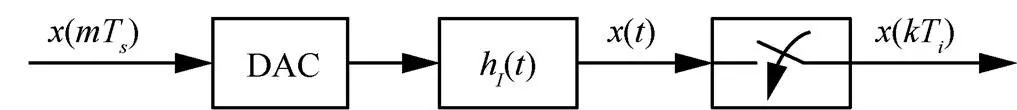
圖2 插值模型

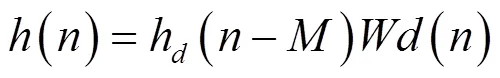
在實際應用時，可以根據實際需求選擇不同類型的窗函數，以漢明窗為例，有

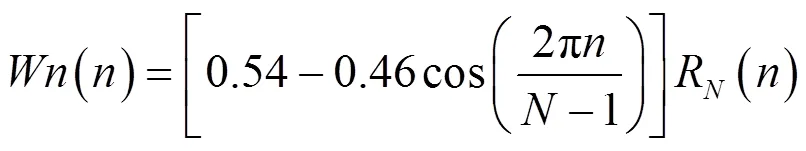
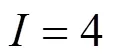
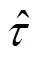
3.2 設定搜索步長

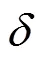
由于在實際系統中，CRB很難精確獲得，本文采用時延估計的修正克拉美羅界[13]（MCRB, modified Cramer-Rao bound）為

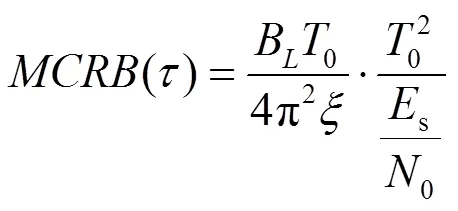
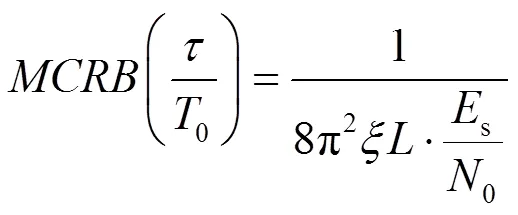
因此，搜索步長可以設定為

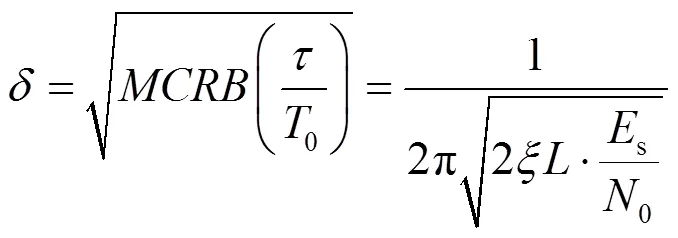
即時延估計標準差的最小值。

3.3 縮小搜索范圍

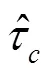
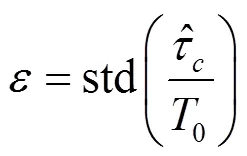
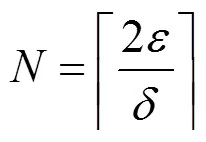
搜索次數由所用前向算法的估計性能與MCRB共同決定，一般來說，在實際應用中遍歷搜索次數不會超過10次，因此，增加的計算量也并非不可接受。

3.4 算法流程

至此，根據圖3所示的原理，本文算法的流程總結如下。

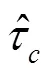
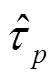
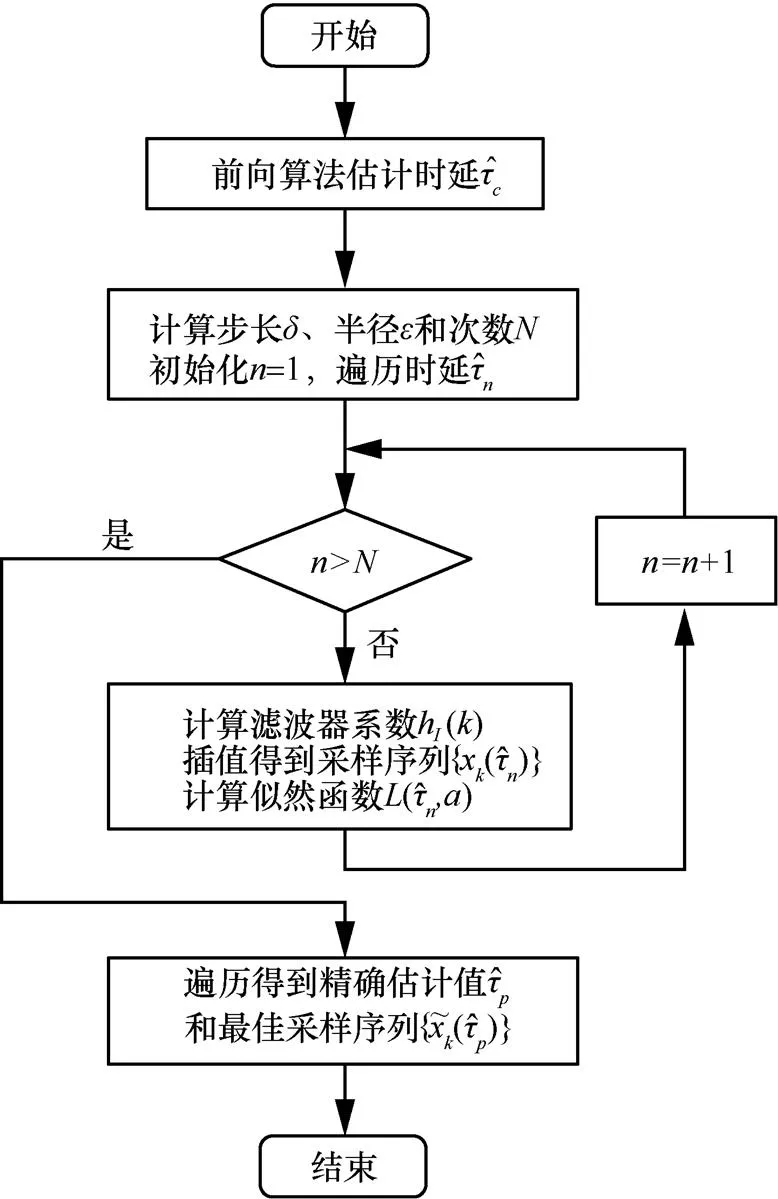
圖3 本文算法原理

4 仿真實驗與性能分析

4.1 插值計算精度的仿真實驗

插值算法的計算精度采用解調所得星座點的方差，描述為

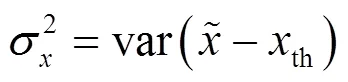
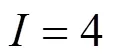
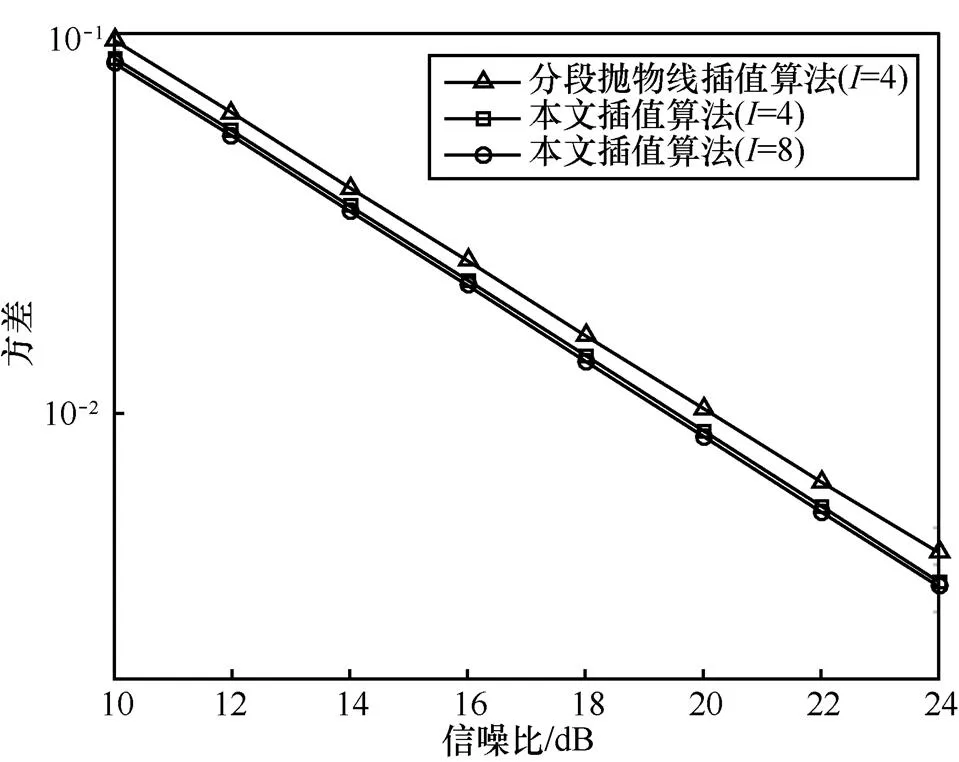
圖4 3種插值算法的方差與信噪比的關系

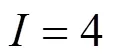
4.2 時延估計精度的仿真實驗

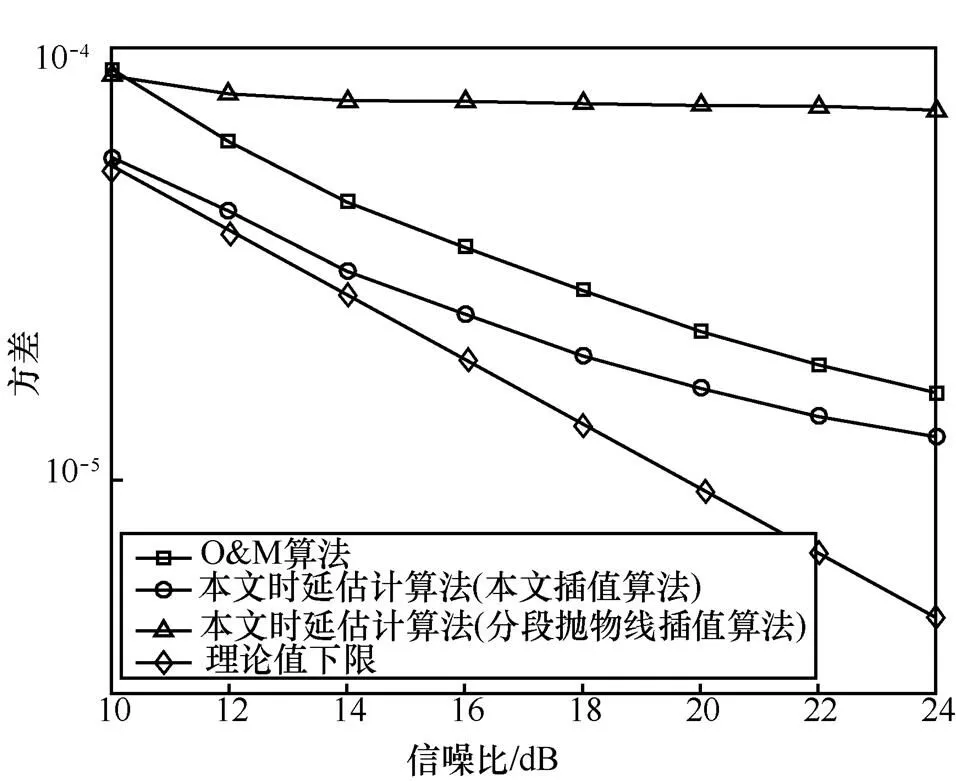
圖5 3種時延估計算法的方差與信噪比的關系

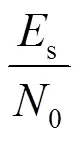
4.3 輻射源識別的仿真實驗

4.3.1 仿真信號

為了使實驗易于理解且更具可重復性，本節采用文獻[7]中的I/Q不平衡模型產生仿真信號。根據上述模型，攜帶I/Q不平衡畸變的基帶復信號可以表示為

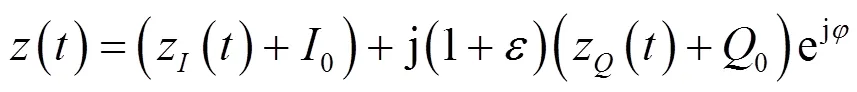
實驗首先根據式(15)仿真產生5個不同的輻射源，其畸變參數設定如表1所示。在每個信噪比下，每個輻射源包含1 000個信號樣本，其中，500個用于訓練，500個用于測試。采用文獻[5,7]中的方法提取細微特征：文獻[5]方法的特征向量由相位錯誤、幅度錯誤、錯誤矢量幅度和原點偏置等組成；文獻[7]的特征向量由上述4個畸變參數的估計值組成。在特征提取完成之后，采用基于徑向基（RBF, radial basis function）核函數的支持向量機（SVM, support vector machine）進行分類識別，分類器使用默認參數。

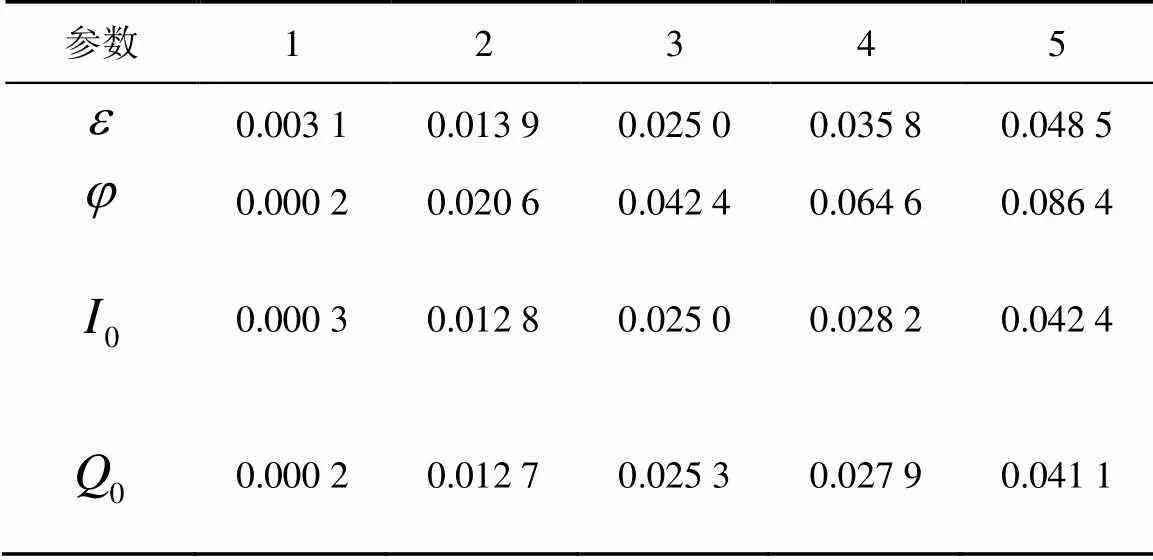
表1 5個輻射源的畸變參數

在接收信號的預處理環節，本節分別對常規符號同步算法（O&M算法估計時延、分段拋物線插值計算最佳采樣序列）和本文符號同步算法進行對比，在得到實際的星座點之后，進行特征提取和分類識別。圖6給出了上述2種符號同步算法的識別率對比。

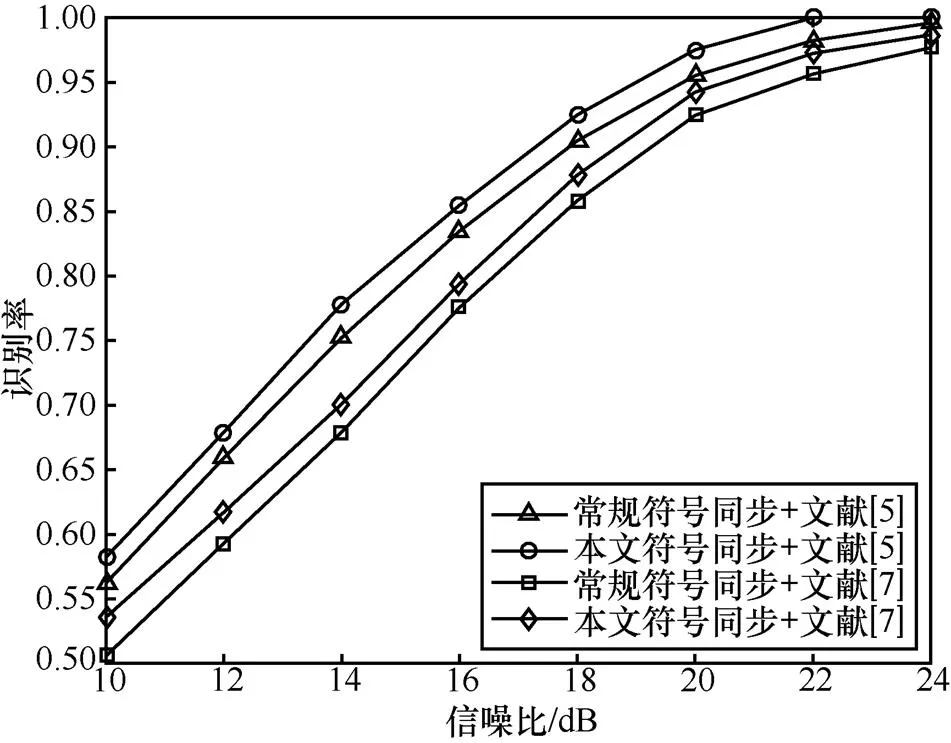
圖6 2種符號同步算法的識別率對比

由圖6可以看出，盡管分別采用了文獻[5]和文獻[7]的方法提取細微特征，但在相同條件下，與常規符號同步算法相比，本文符號同步算法均能夠帶來約2%~3%識別率的提高，這是因為本文算法在時延估計精度和插值計算精度這2個方面均做出了針對性的改進，較好地解決了現有方法遇到的問題，得到的實際星座點能夠更好地保持輻射源固有的個體差異，從而提高了個體的識別率。值得注意的是，雖然實驗中采用的是文獻[5]和文獻[7]的特征提取方法，但本文所提的高精度符號同步算法通用于任何以信號解調為基礎的特征提取算法。

4.3.2 實際信號

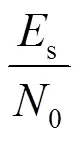
由于樣本的頻偏波動較大，為了避免其對特征提取算法的干擾，在實驗過程中，先對每個樣本估計并去除頻偏。采用文獻[5]的PARADIS提取細微特征，并利用RBF-SVM進行分類識別。在預處理環節，分別利用常規符號同步算法和本文符號同步算法進行對比。表2和表3分別給出了2種符號同步算法的識別結果。為了方便觀察，圖7給出了分別采用上述2種符號同步算法得到的部分特征的分布圖，這里僅選取了相位錯誤、原點在I軸和Q軸上的偏置這三維特征。

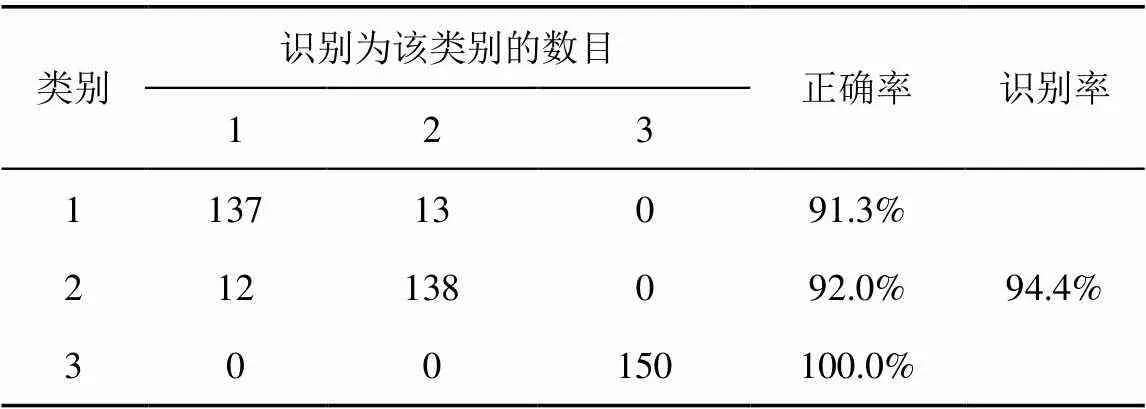
表2 常規符號同步算法的識別結果

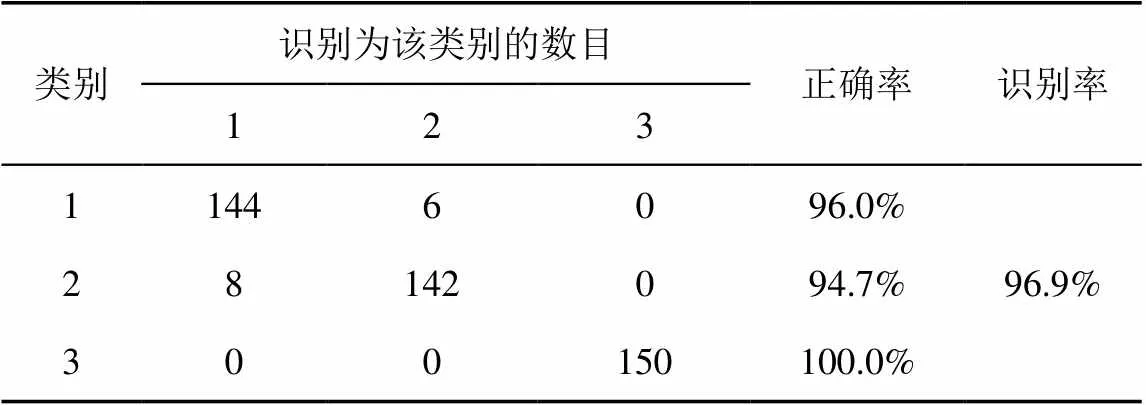
表3 本文符號同步算法的識別結果

由圖7可以看出，與常規符號同步算法相比，由本文算法得到的部分特征的分布呈現出了更明顯的類內聚、類間散的特點，取得了更好的識別結果。這是因為本文算法提高了符號同步的處理精度，減弱了人為引入的處理誤差，更好地保持了輻射源的個體特征。表2和表3的識別結果證明本文算法具有較好的實際效果。

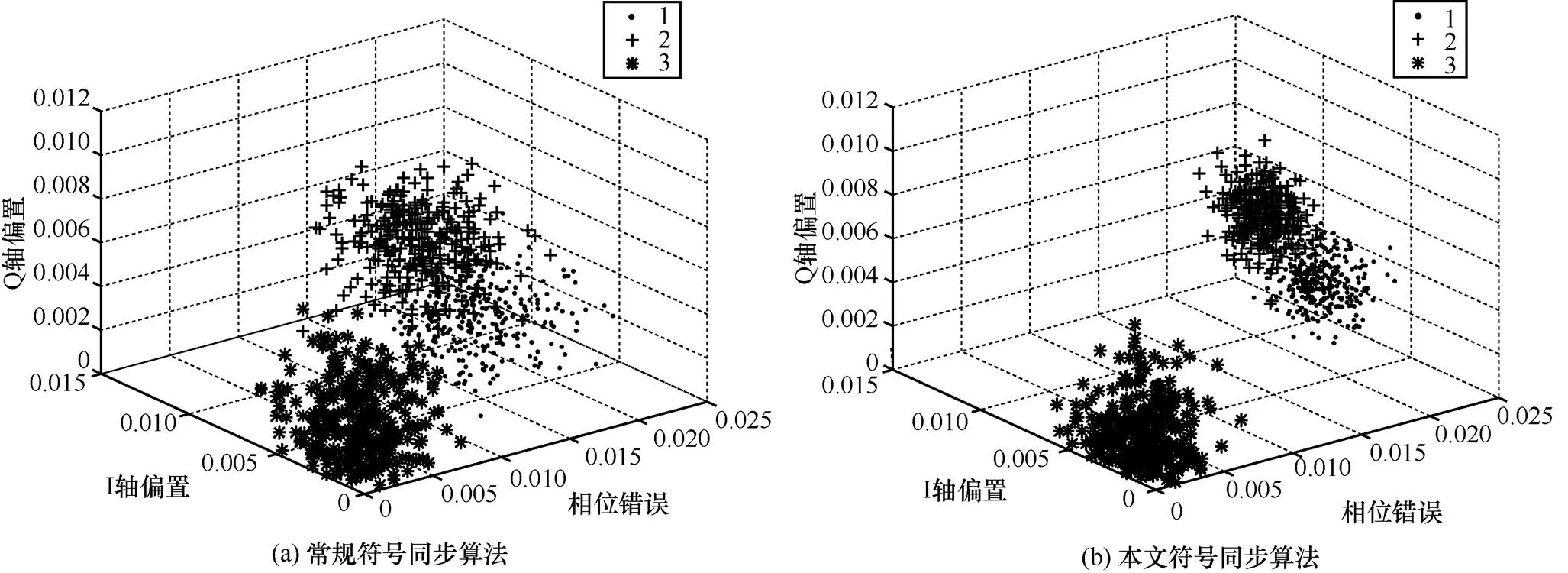
圖7 部分特征的分布

5 結束語

本文針對現有符號同步方法直接應用于SEI預處理環節面臨的問題，分別通過優化插值濾波器的設計和采用數據輔助的方式，提高了插值計算和時延估計的精度，更適用于提取輻射源的細微特征。仿真結果表明，在相同條件下，本文算法能夠帶來約2%~3%識別率的提高。

雖然本文只涉及解調過程的符號同步環節，但是載頻、符號速率等參數的估計以及載波同步等環節同樣需要引起重視，SEI的預處理流程有待規范統一。

[1] 蔡忠偉, 李建東. 基于雙譜的通信輻射源個體識別[J]. 通信學報, 2007, 28(2): 75-79.

CAI Z W, LI J D. Study of transmitter individual identification based on bispectra[J]. Journal on Communications, 2007, 28(2): 75-79.

[2] 韓潔, 張濤, 王歡歡, 等. 基于3D-Hibert能量譜和多尺度分形特征的通信輻射源個體識別[J]. 通信學報, 2017, 38(4): 99-109.

HAN J, ZHANG T, WANG H H, et al. Communication emitter individual identification based on 3D-Hibert energy spectrum and multi-scale fractal features[J]. Journal on Communications, 2017, 38(4): 99-109.

[3] BERTONCINI C, RUDD K, NOUSAIN B, et al. Wavelet fingerprinting of radio-frequency identification (RFID) tags[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4843-4850.

[4] ZHANG J, WANG F, DOBRE O A, et al. Specific emitter identification via Hilbert-Huang transform in Single-Hop and relaying scenarios[J]. IEEE Transactions on Information Forensics & Security, 2016, 11(6): 1192-1205.

[5] BRIK V, BANERJEE S, GRUTESER M, et al. Wireless device identification with radiometric signatures[C]// ACM International Conference on Mobile Computing and Networking. 2008: 116-127.

[6] HUANG Y L, ZHENG H. Radio frequency fingerprinting based on the constellation errors[C]// Communications. 2012:900-905.

[7] 王大海. 衛星通信輻射源細微特征提取技術研究[D]. 鄭州: 解放軍信息工程大學, 2015.

WANG D H. Research on the extraction technology of satellite communication transmitter fine features[D]. Zhengzhou: PLA Information Engineering University, 2015.

[8] 黃淵凌, 鄭輝. 一種基于相噪特性的輻射源指紋特征提取方法[J]. 計算機仿真, 2013, 30(9): 182-185.

HUANG Y L, ZHENG H. Emitter fingerprint feature extraction based on characteristics of phase noise[J]. Journal of Computer Simulation, 2013, 30(9): 182-185.

[9] ERUP L, GARDNER F M, HARRIS R A. Interpolation in digital modems II Implementation and performance[J]. IEEE Transactions on Communications, 1993, 41(6): 998-1008.

[10] GOETHALS K, MOENECLAEY M. PSK symbol synchronization performance of ML-oriented data-aided algorithms for nonselective fading channels[J]. IEEE Transactions on Communications, 2002, 43(234): 767-772.

[11] GARDNER F M. Interpolation in digital modems I Fundamentals[J]. IEEE Transactions on Communications, 1993, 41(3): 501-507.

[12] 李天昀, 許漫坤, 葛臨東. 取鄰抽取任意倍數采樣率變換算法[J]. 數據采集與處理, 2012, 27(2): 254-258.

LI T Y, XU M K, GE L D. Conversion algorithm between arbitrary sampling rate based on neighbor decimation[J]. Journal of Data Acquisition&Processing, 2012, 27(2): 254-258.

[13] D'ANDREA A N, MENGALI U, REGGIANNINI R. The modified Cramer-Rao bound and its application to synchronization problems[J]. IEEE Transactions on Communications, 1994, 42(234): 1391-1399.

[14] OERDER M, MEYR H. Digital filter and square timing recovery[J]. IEEE Transactions on Communications, 1988, 36(5): 605-612.

High-precision symbol timing algorithm for specific emitter identification

PAN Yiwei, PENG Hua, LI Tianyun, WANG Wenya

Institute of Information Systems Engineering, Information Engineering University, Zhengzhou 450001, China

The existing symbol timing algorithms have the problems that the method of delay estimation is improper and the calculation precision of the interpolation is insufficient for the pretreatment of specific emitter identification. A high-precision symbol timing algorithm was proposed to solve these problems. Aiming at the former problem, a two-step estimation method was adopted, rough estimation of delay was firstly obtained by the forward algorithm, and then the accurate value was acquired through local search with the demodulated symbols. For the latter problem, a window-based approach was used to design an interpolating filter which could optimize the anti-aliasing characteristics and improve the calculation accuracy. Simulation results show that the proposed algorithm can effectively solve the above problems and achieve better recognition results in the radiation source recognition compared with the conventional symbol timing algorithm.

specific emitter identification, high precision, symbol timing, delay estimation, interpolating filter

TN911.7

A

10.11959/j.issn.1000?436x.2018132

潘一葦（1990?），男，山東青島人，信息工程大學博士生，主要研究方向為通信信號處理、特定輻射源識別等。

彭華（1973?），男，江西萍鄉人，信息工程大學教授、博士生導師，主要研究方向為軟件無線電和通信信號處理。

李天昀（1979?），男，江西萍鄉人，信息工程大學副教授、碩士生導師，主要研究方向為軟件無線電、通信信號處理等。

王文雅（1991?），女，湖北天門人，信息工程大學碩士生，主要研究方向為通信信號處理。

2017?12?25：

2018?04?09

國家自然科學基金資助項目（No.61401511）

The National Natural Science Foundation of China (No.61401511)