內(nèi)部熱耦合塔的傳熱研究

方 靜，刁夢宇，李春利，劉 慶，趙睿琛

（河北工業(yè)大學(xué) 化工學(xué)院，天津 300130）

精餾是目前工業(yè)上廣泛應(yīng)用的分離單元之一，同時也是高能耗、低熱力學(xué)效率的化工操作單元。分離過程的能耗占化工行業(yè)總能耗的40%～60%，而精餾所需的能耗約為分離過程總能耗的95%，熱力學(xué)效率僅為5%～10%。內(nèi)部熱耦合塔（HIDiC）由于塔間的內(nèi)部熱量耦合作用，在降低了冷凝器和再沸器熱負(fù)荷的同時，也增強了精餾操作過程中的可逆性，提高了熱力學(xué)效率，可節(jié)能30%～60%［1］。1986年，Nakaiwa等［2-3］在對HIDiC的理論研究和實驗研究中證明了HIDiC具有出色的節(jié)能效果。Campbell等［4］通過增強精餾操作過程的可逆性，證明了HIDiC具有較高的熱力學(xué)效率及巨大的節(jié)能潛力。Xu等［5-8］對HIDiC的傳熱系數(shù)進行了實驗研究，得出總傳熱系數(shù)隨兩塔間傳熱推動力的增大而減小的規(guī)律。Iwakabe等［9］將HIDiC用于多組分的分離，驗證了它具有較高的能量效率。

本工作以中試規(guī)模的同軸HIDiC為研究對象，計算了傳熱過程中兩塔段間的實際傳熱量，并根據(jù)模擬數(shù)據(jù)分析了兩塔段由于傳熱產(chǎn)生的內(nèi)回流量和蒸汽增量，考慮到這部分流量的增加會形成熱阻阻礙熱量傳遞等因素，確定了該塔的最佳操作壓縮比。

1 HIDiC的實驗研究

1.1 實驗裝置與實驗步驟

HIDiC實驗裝置見圖1，塔的各項參數(shù)見表1。

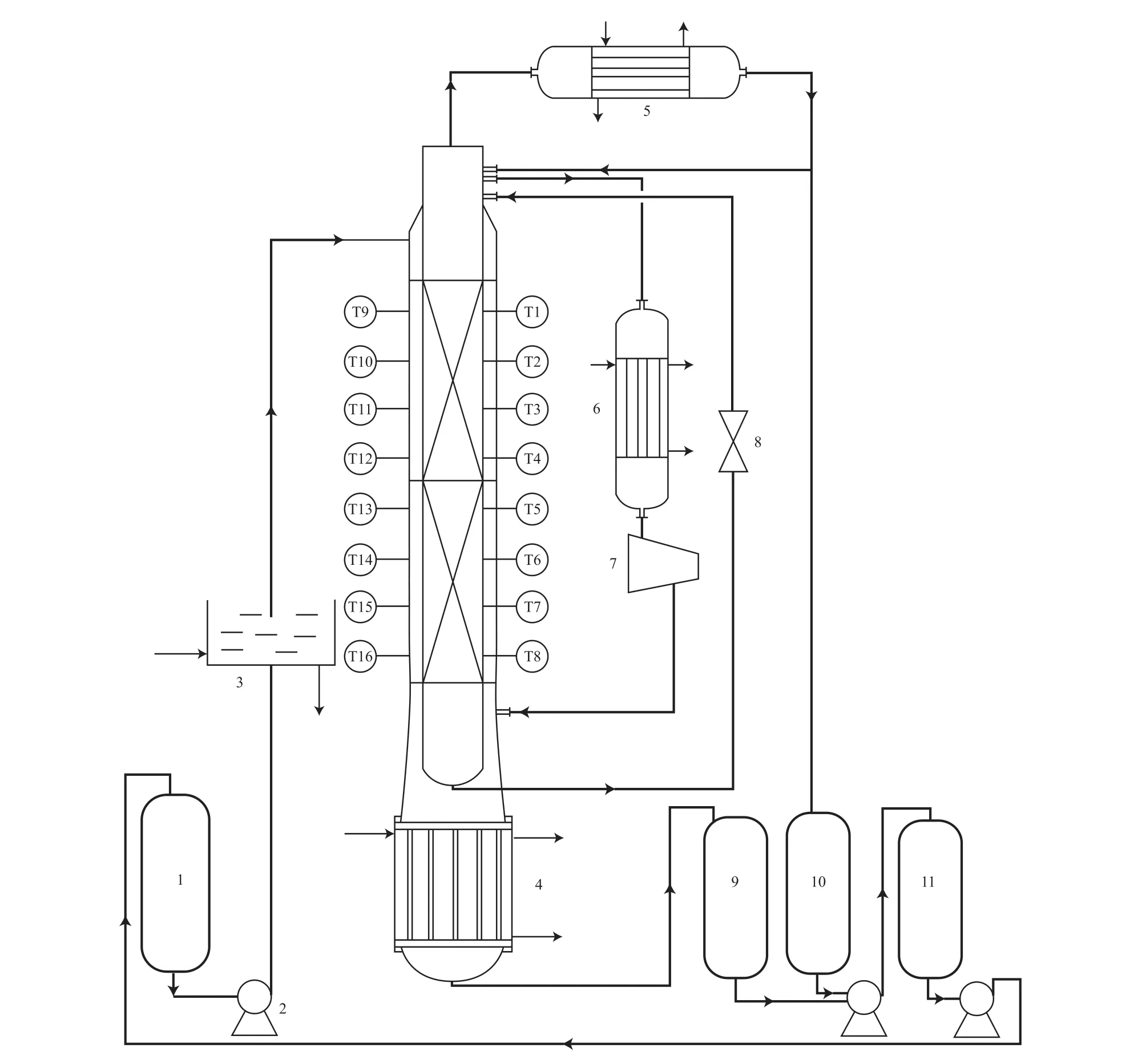
圖1 HIDiC實驗裝置Fig.1 Internally heat-integrated distillation column(HIDiC) experimental setup.

本研究以乙醇-水為待分離物系。兩塔段均采用304不銹鋼材質(zhì)，原料經(jīng)進料齒輪泵打入提餾段頂部，精餾段塔頂產(chǎn)品經(jīng)冷凝器冷凝，一部分回流到精餾段頂部，一部分采出到輕組分罐，塔釜產(chǎn)品直接采出到重組分槽；內(nèi)塔和外塔之間的傳質(zhì)通過壓縮機和節(jié)流閥完成，提餾段頂部氣相經(jīng)預(yù)熱器、壓縮機后，被加壓到精餾段底部，內(nèi)塔底部液相經(jīng)減壓閥被送入外塔進料板處，精餾段壓力必須足夠高，以提供有效的換熱溫差。該裝置共安裝了16個測溫點，精餾段有8個測溫點（T1～T8）、提餾段有有8個測溫點（T9～T16）。本實驗的各項操作參數(shù)見表2。實驗最終實現(xiàn)了在壓縮比1.4～2.6下穩(wěn)定操作的基礎(chǔ)上進行連續(xù)進料和采出，產(chǎn)品純度通過氣相色譜儀測定。

表1 HIDiC的主要參數(shù)Table 1 Main parameters of HIDiC

表2 實驗條件參數(shù)Table 2 Parameters of experiment

1.2 內(nèi)部熱耦合對溫度和溫差的影響

在連續(xù)操作狀態(tài)下，通過改變壓縮機排氣跟蹤值來調(diào)節(jié)精餾段與提餾段之間的壓縮比，當(dāng)壓縮比為1.5～2.6（步長為0.1）時，記錄全塔各溫度測量點的溫度，繪制HIDiC的溫度分布圖，結(jié)果見圖2。

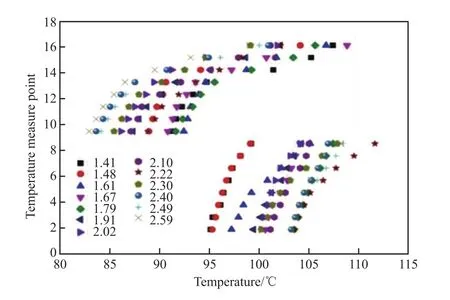
圖2 不同壓縮比下全塔的溫度分布圖Fig.2 Diagram of temperature distribution at different compression ratios.

從圖2可看出，由于精餾段為高壓操作，它的溫度整體高于提餾段，并且在同一壓縮比下，精餾段各測溫點的溫度相對于提餾段變化平緩。這主要是由于整個精餾段的內(nèi)壁作為該傳熱過程中的換熱面，在內(nèi)外塔傳熱溫差的推動下，精餾段的內(nèi)部均勻地向外散熱；而實際過程中提餾段除了接收精餾段放出的熱量外，塔釜還集中通過高溫蒸汽給塔內(nèi)供熱，致使該塔段內(nèi)壓降較大，約為5 kPa。表3以壓縮比2.6為例，給出了各塔板上輕組分的質(zhì)量組成（該結(jié)果為與實驗操作條件保持一致時的模擬結(jié)果）。從表3可看出，精餾段內(nèi)各塔板上的汽液平衡濃度的變化幅度相對于提餾段較小，這也是造成兩塔段內(nèi)溫度變化趨勢不同的原因之一。

根據(jù)實驗數(shù)據(jù)繪制了不同壓縮比下兩塔段對應(yīng)測溫點（見圖1）間的溫差，如圖3所示。由圖3可見，壓縮比小于1.7時，第一對測溫點位置處的溫差為負(fù)，即在該位置熱量從提餾段傳向精餾段，這主要由于壓縮比較低時，精餾段增溫較少，會低于通過再沸器直接蒸汽加熱的提餾段。并且，壓縮比為1.7時，有各別對應(yīng)溫度點的溫差剛好為0。為了實現(xiàn)有效的正向傳熱推動力，在后續(xù)對HIDiC傳熱的分析中，將該塔的可壓縮比范圍縮小到 1.8～2.6。

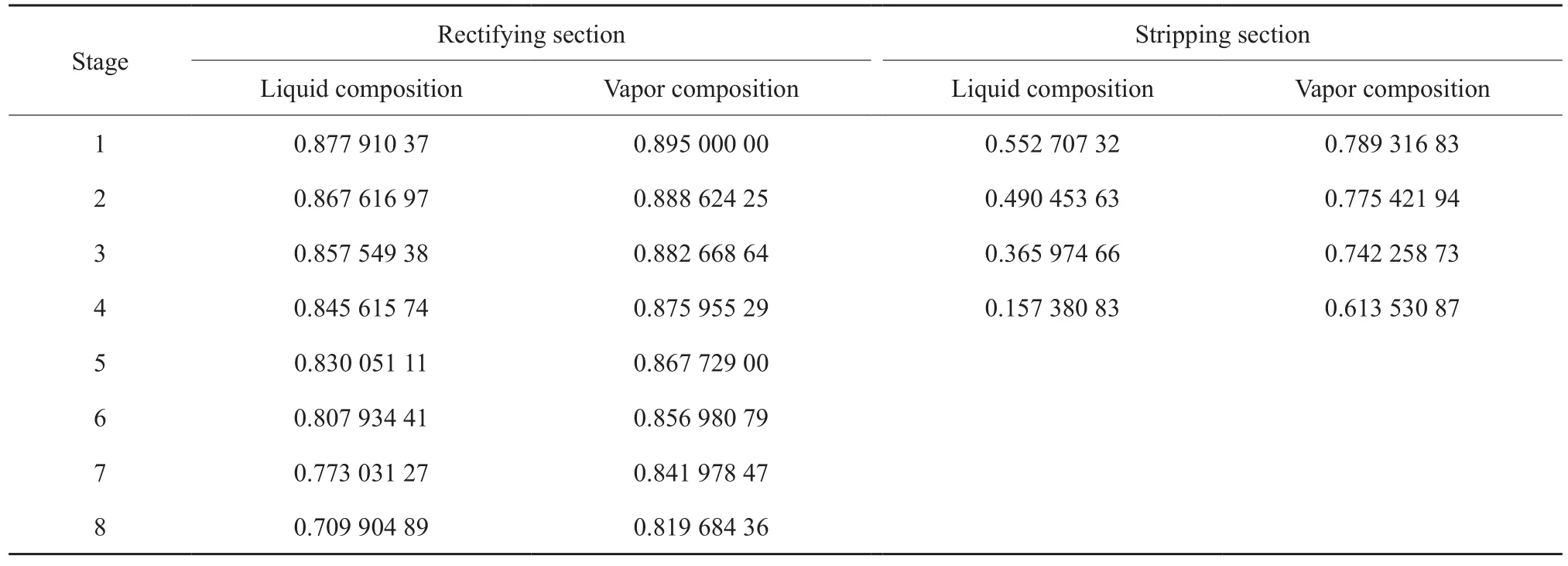
表3 乙醇-水物系在壓縮比2.6時塔板上的質(zhì)量組成Table 3 The mass composition of the ethanol-water system on the column tray at the compression ratio of 2.6

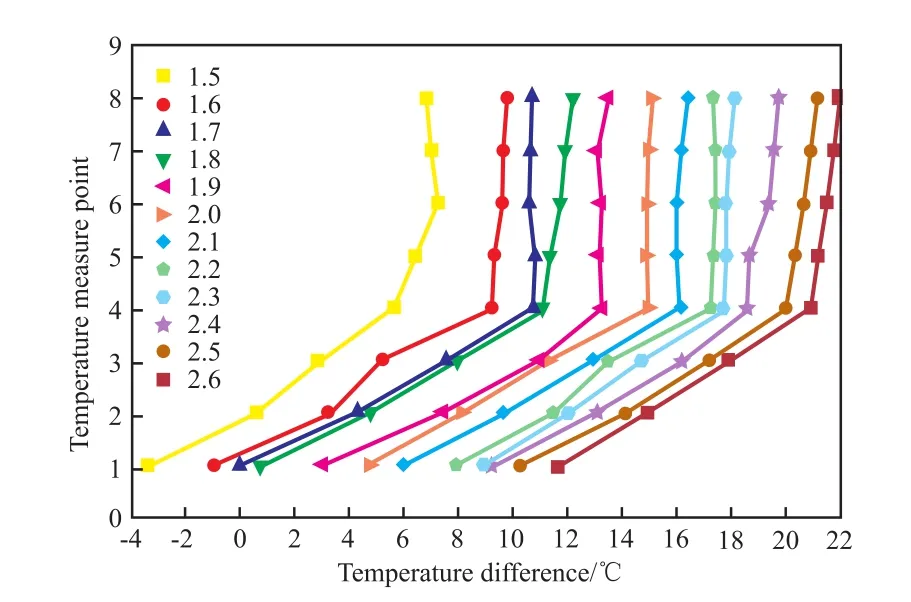
圖3 精餾段與提餾段對應(yīng)溫度測量點間的溫差Fig.3 Temperature differences between the corresponding temperature measurement points of rectifying section and stripping section.

1.3 全塔熱量損失的計算

本工作同時測量了塔身保溫層最外部的溫度，由此可計算全塔的熱損失。本實驗裝置的熱損失主要是提餾段向環(huán)境散熱導(dǎo)致的熱量散失，可用式（1）和式（2）計算。考慮到散熱過程為大空間自然對流傳熱，根據(jù)本實驗裝置的結(jié)構(gòu)尺寸，可按照豎直圓管處理，對流傳熱系數(shù)的計算公式見式（3）和式（4）。定性溫度下空氣的物理性質(zhì)［10］見表4，提餾段的相關(guān)計算參數(shù)見表5。經(jīng)計算可得，整個塔身（不包含管道）的散熱面積為7.56 m2、定性溫度為34 ℃、系數(shù)C與n分別為0.135和1/3，最終得到的自然對流傳熱系數(shù)為4.75 W/（m2·℃），則該塔向環(huán)境散失的熱量，即熱損失Qloss，為1 005.48 W。

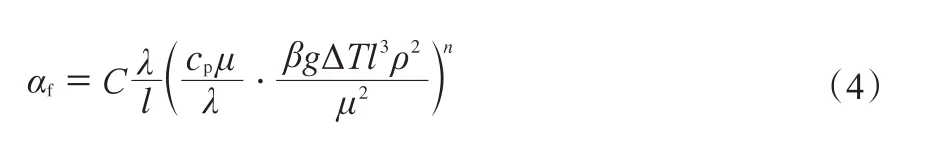
式中，Ad為散熱面積，m2；d為加保溫層后提餾段的直徑，m；l為塔高（不加封頭），m；Qloss為熱損失，W；αf為傳熱系數(shù)，W/（m2·℃）；ΔT為保溫層與環(huán)境之間的溫差，℃；tm為定性溫度，℃；tI為保溫層溫度，℃；tE為環(huán)境溫度，℃；β為1/T，按理想氣體計算，K-1；C，n為公式系數(shù)；λ，μ，ρ，cp分別為空氣的導(dǎo)熱系數(shù)、黏度、密度和熱導(dǎo)率，相應(yīng)數(shù)值在表4中列出；g為氣體常數(shù)，取8.314 J/（mol·K）。

表4 定性溫度下空氣的物理性質(zhì)［10］Table 4 Physical properties of atmosphere under the qualitative temperature［10］

表5 提餾段的相關(guān)計算參數(shù)Table 5 Calculation parameters of stripping column section

1.4 內(nèi)部熱耦合對傳熱量的影響

獲取了不同壓縮比下兩塔段的總傳熱量和對數(shù)平均溫差后，可計算兩塔段之間的總傳熱系數(shù)。在此值得注意的是，HIDiC的總傳熱量與塔釜熱負(fù)荷的關(guān)系與有中間換熱器的精餾過程相同［11］，即完成相同分離任務(wù)時，HIDiC的再沸器熱負(fù)荷與總傳熱量之和等于傳統(tǒng)精餾塔的再沸器熱負(fù)荷，見式（5）。在確保傳統(tǒng)精餾塔與HIDiC達(dá)到相同分離要求的前提下，通過Aspen Plus軟件模擬，可得到傳統(tǒng)塔再沸器的負(fù)荷。

式中，QR′eb為再沸器熱負(fù)荷，kW；QReb為傳統(tǒng)精餾塔再沸器的負(fù)荷，kW；QT為HIDiC兩塔段間的總傳熱量，kW。

考慮到實驗時的熱損失，QT應(yīng)按式（6）計算：

其中，QR′eb通過式（7）計算：

式中，m為蒸汽冷凝水的質(zhì)量流量，kg/s；r為水的汽化潛熱，kJ/kg；c為水的比熱容，kJ/（kg·℃）；Δt′為蒸汽的進出口溫差，℃。

由于提餾段在各壓縮比下的操作壓力大致相同，實驗中所測得的保溫層外表面溫度在不同操作條件下均一致，因此不同操作條件下的熱損失也一致，均取1.3節(jié)的計算值1 005.48 W。將測量得到的一系列再沸器熱負(fù)荷和熱損失代入式（6），可得到壓縮比的變化對總傳熱量的影響，如圖4所示。從圖4可看出，壓縮比小于2.0時，隨著壓縮比的增大，總傳熱量逐漸增大；壓縮比大于2.0后，總傳熱量略有下降，變化不大。實驗中出現(xiàn)的熱阻將在后續(xù)模擬中給出。

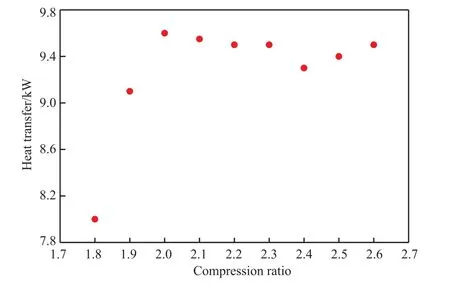
圖4 壓縮比對總傳熱量的影響Fig.4 Effects of compression ratios on amount of total heat transfer.

2 HIDiC的模擬研究

2.1 模擬步驟及方法

在運用Aspen Plus對HIDiC進行模擬之前，首先對滿足進料條件和分離要求、同時符合總進料板數(shù)和進料位置等的常規(guī)精餾塔進行設(shè)計。對于HIDiC的模擬，首先會有一個僅使用壓縮機提高精餾段壓力，但兩塔段之間還沒有進行熱量耦合的虛擬過渡階段，稱為絕熱HIDiC。最后是加入熱量耦合的同軸HIDiC。模擬中傳熱量的指定通過軟件中的heater and cooler模塊和pump-around模塊實現(xiàn)。

目前常用的分配方式主要有換熱量平均分配和熱溫匹配兩種［12-13］。由于在HIDiC中沿塔高從上到下每對測溫點之間的溫差變化很大，而傳熱系數(shù)是物系的物性參數(shù)，各物性參數(shù)又是溫度的函數(shù)，所以全塔各對應(yīng)測溫點間的傳熱系數(shù)不是一個定值，且每對塔板之間的換熱量也不相同，因此上述兩種熱量分配方式均存在一定的誤差。本工作不采用上述兩種熱量分配方式，而是致力于通過計算的方式確定每對測溫點之間的總傳熱系數(shù)，并用于兩塔段之間換熱量的計算以及后續(xù)HIDiC的傳熱研究。

2.2 傳熱模型的建立與驗證

本工作采用一種以乙醇-水物性數(shù)據(jù)為基礎(chǔ)計算HIDiC傳熱量的方法［14-18］。因為精餾段和提餾段內(nèi)氣相和液相均處于飽和狀態(tài)，兩塔段間的熱量耦合促使內(nèi)塔向外塔傳熱，這一行為會使兩塔段內(nèi)的流體發(fā)生相變，所以精餾段和提餾段內(nèi)的對流給熱系數(shù)分別為冷凝給熱系數(shù)和沸騰給熱系數(shù)，它們的計算見式（8）～（10）。其中，各物性參數(shù)均為溫度的函數(shù)，溫度值可通過實驗測得。

精餾段的冷凝對流給熱系數(shù)的計算：

當(dāng)（GaPrK″）＜ 1015時，

當(dāng)（GaPrK″）＞ 1015時，

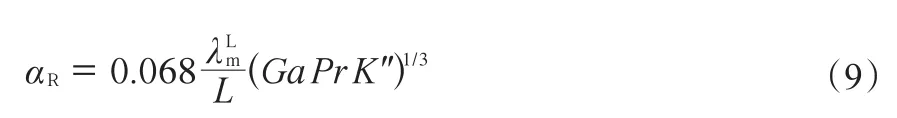
式中，αR為冷凝對流給熱系數(shù)，W（/m2·K）；為冷凝液的導(dǎo)熱系數(shù)，W（/m·K）；為冷凝液的黏度，Pa·s；為冷凝液的密度，kg/m3；L為換熱面的長度，m；Δt為精餾段與提餾段對應(yīng)位置上的溫差，℃；Ga為無量綱數(shù)，K″為無量綱數(shù)為冷凝液的普朗特數(shù)。

提餾段的沸騰對流給熱系數(shù)的計算：

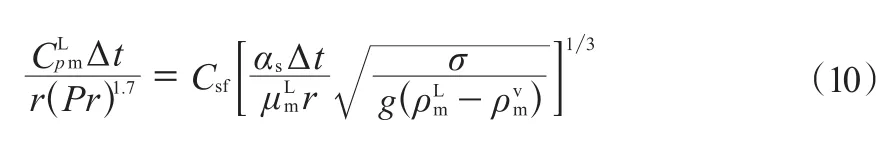
式中，αS為沸騰對流給熱系數(shù)，W（/m2·K）；為飽和蒸汽的密度，kg/m3；σ為氣-液界面的表面張力，N/m；Csf為組合常數(shù)。

該塔對應(yīng)位置間的傳熱系數(shù)可由式（11）得到。

式中，ki為對應(yīng)位置間的傳熱系數(shù)，W/（m2·K）；δ為精餾段厚度，m；λw為精餾段塔壁的導(dǎo)熱系數(shù)，W/（m2·K）。

對應(yīng)位置間的傳熱量Qi可由式（12）進行計算。

式中，Ai為對應(yīng)傳熱位置的面積，m2，Ai=πdiLp；di為精餾段的塔內(nèi)徑，m；Lp為有效換熱長度，即塔內(nèi)填料高度，為2.8 m。實驗中一共8組測溫點，則每個對應(yīng)傳熱位置的面積Ai為總面積的1/8，進而得到塔段間的總傳熱量QT：

將計算得到的精餾段與提餾段對應(yīng)測溫點間的換熱量帶入Aspen plus軟件進行模擬，模擬的主要參數(shù)與連續(xù)實驗操作參數(shù)保持一致，并采用Wilson熱力學(xué)模型。以壓縮比2.2為例，將模擬得到的溫度與實驗溫度進行對比，結(jié)果見圖5。從圖5可看出，模擬得到的溫度值與實驗值在誤差允許范圍內(nèi)吻合良好，推測誤差原因是實驗中環(huán)形壁流現(xiàn)象以及液膜自上而下厚度變化的影響。擬合結(jié)果表明計算傳熱量的方法在一定范圍內(nèi)切實可行，對傳熱分析的模擬準(zhǔn)確有效。

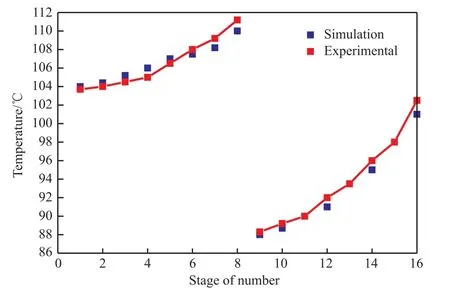
圖5 溫度的模擬值與實驗值的對比Fig.5 Simulation and experimental temperature comparison chart.Compression ratio was 2.2.

2.3 HIDiC塔段內(nèi)汽液相流量的變化

同軸式HIDiC加入傳熱后，由于塔間的熱耦合作用，從精餾段取熱，使得精餾段內(nèi)塔板上的上升蒸汽部分冷凝，冷凝后的液體又返回該塔板并流向下一層塔板，這樣進入上層塔板的汽相流量相應(yīng)減少，流入下一層塔板的液相流量相應(yīng)增加。所以從整體看，會出現(xiàn)從精餾段底部塔板到頂部塔板汽相流量依次下降，從頂部塔板到底部塔板液相流量依次增加的情況。而且隨著壓縮比的增大，兩塔段間的傳熱溫差增大，熱量耦合作用增強，精餾段給出的熱量愈多，汽液相流量的變化幅度愈大。提餾段與之類似，熱耦合的作用是為其供熱，塔板上的下降液體部分蒸發(fā)，使得上升到上一層塔板的汽相流量增多，下降到下一層塔板的液相流量減少。所以從整體看，就會出現(xiàn)從提餾段底部塔板到頂部塔板汽相流量依次增大，從頂部塔板到底部塔板液相流量依次減少的情況。同樣地，熱耦合作用隨壓縮比增大逐漸增強，提餾段接收的熱量愈多，塔內(nèi)汽液相流量的變化幅度愈大。兩塔段汽液相流量的變化如圖6所示。由圖6可見，在任意的N-1，N，N+1三塊塔板上，汽相（V）和液相（L）流量在兩塔段中呈現(xiàn)不同的變化情況，在精餾段內(nèi)流量的變化情況為L＜L′＜L″，V＜V′＜V″；在提餾段內(nèi)流量的變化情況為L＜L′＜L″，V＞V′＞V″。

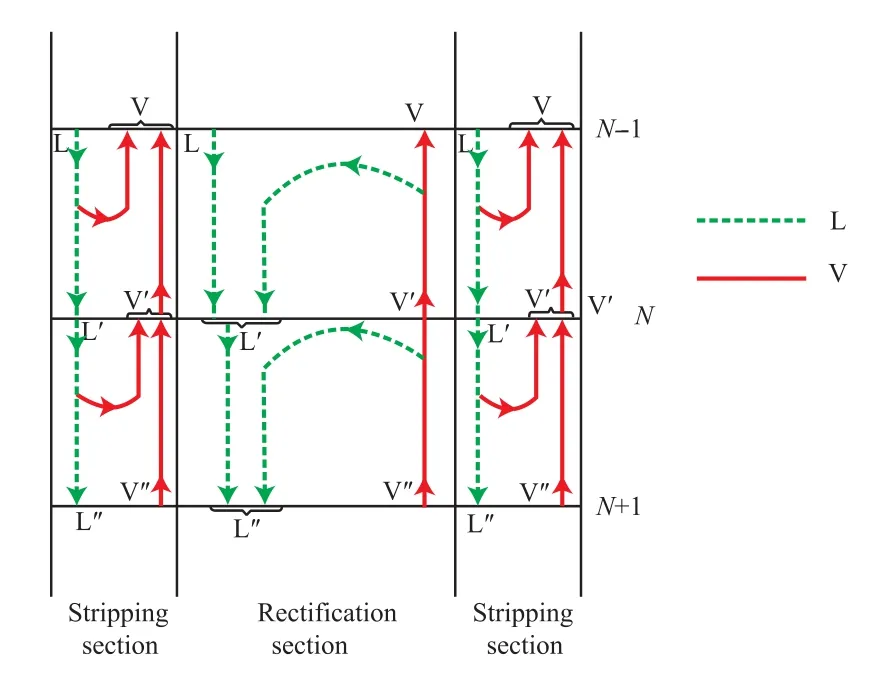
圖6 HIDiC中兩塔段汽液流量的變化Fig.6 The vapor and liquid flow changes in the two column sections of HIDiC.

本工作認(rèn)為與絕熱HIDiC相比，精餾段每塊塔板上的液相增量之和即為該塔段由于熱耦合作用產(chǎn)生的內(nèi)回流量，提餾段每塊塔板上的汽相增量之和即為該塔段由于熱耦合作用產(chǎn)生的蒸汽增量。HIDiC在不同壓縮比下的內(nèi)回流量和蒸汽增量如圖7所示。由圖7可見，隨著壓縮比的增大，精餾段的內(nèi)回流量和提餾段的蒸汽增量均不斷增大。

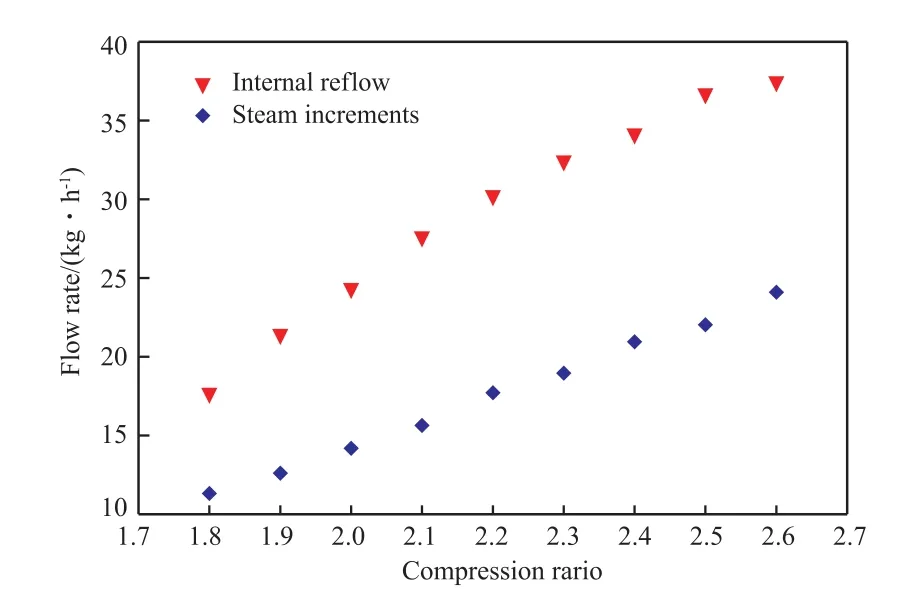
圖7 HIDiC在不同壓縮比下的內(nèi)回流量和蒸汽增量Fig.7 The internal reflow and steam increments of HIDiC at different compression ratios.

2.4 總傳熱量的模擬值與實驗值的對比分析

將不同壓縮比下總傳熱量的計算值與實驗值進行對比，結(jié)果如圖8所示。從圖8可看出，壓縮比小于2.2時，總傳熱量的計算值略小于實驗值，并且兩者吻合度較好；當(dāng)壓縮比大于2.2時，計算值顯著大于實驗值，且兩者的差距隨壓縮比的增大而增大。產(chǎn)生這種現(xiàn)象的原因有兩個：1）隨壓縮比的增大，兩塔段間的溫差增大，傳熱推動力增大，相應(yīng)地傳熱量的計算值也增大；2）在實際操作中，壓縮比增大，傳熱量也增大，表現(xiàn)為內(nèi)回流量和蒸汽增量的增大。而內(nèi)回流量增大，精餾段塔壁上的液膜增厚，會在一定程度上增大傳熱過程中的熱阻；提餾段內(nèi)蒸汽增量增大，當(dāng)汽化速率大于液體流向內(nèi)壁的速率時，內(nèi)壁表面會出現(xiàn)“干點”，甚至形成一層氣膜，阻礙熱量傳遞。由于在計算過程中，兩塔段內(nèi)傳熱出現(xiàn)的這部分熱阻未被考慮，因此在實際過程中，壓縮比較大時傳熱量趨于平緩甚至略有下降，所以當(dāng)壓縮大于2.2時，總傳熱量的計算值大于實驗值且隨著壓縮比的增大而增大。

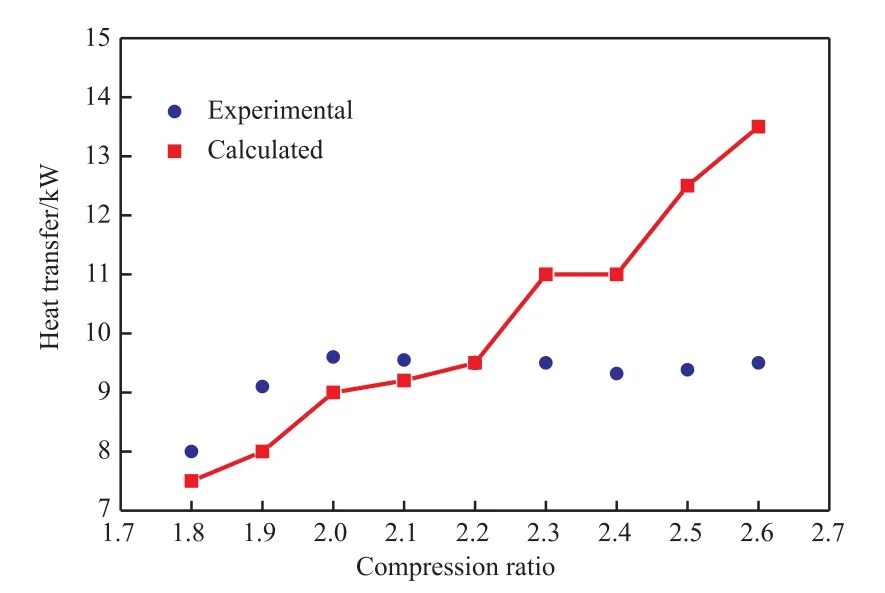
圖8 不同壓縮比下總傳熱量的計算值與實驗值的對比Fig.8 Comparison between calculated and experimental value of total heat transfer at different compression ratios.

由于HIDiC節(jié)能的根本原因是兩塔段間的傳熱使塔頂和塔釜的熱負(fù)荷減少，在一定壓縮比范圍內(nèi)，塔間傳熱量隨壓縮比的增大不斷增加的同時，塔頂和塔釜熱負(fù)荷減小。但考慮到在實際操作中，塔壁兩側(cè)的熱阻也隨壓縮比的增大不斷增加，總能耗也會相應(yīng)增大。綜合各因素，將最佳操作壓縮比定為2.0。

3 結(jié)論

1）以中試規(guī)模的同軸HIDiC為研究對象，選用乙醇-水為待分離物系，分別進行了實驗研究和模擬研究。實驗結(jié)果表明，兩塔段內(nèi)的溫度及塔間對應(yīng)位置間的溫差均隨壓縮比的增大而增大。壓縮比小于1.8時，精餾段的整體溫度并不比提餾段高，為了確保實現(xiàn)精餾段向提餾段傳熱的正向推動力，將該塔的可操作壓縮比范圍縮小到1.8～2.6。考慮熱損失，計算出的該塔實際傳熱量在壓縮比小于2.0時隨壓縮比的增大明顯升高，再繼續(xù)增大壓縮比傳熱量趨于不變。

2）將通過傳熱模型計算得到的傳熱量進行模擬，模擬結(jié)果表明，精餾段的內(nèi)回流量和提餾段的蒸汽增量都隨壓縮比的增大而增加。精餾段內(nèi)回流量的增大、塔壁上液膜的增厚，會在一定程度上增大傳熱過程中的熱阻；提餾段不斷接收熱量，內(nèi)壁下降的液體逐漸發(fā)生汽化，當(dāng)汽化速率大于液體流向內(nèi)壁的速率時，內(nèi)壁表面會出現(xiàn)“干點”，甚至形成一層氣膜，同樣會阻礙熱量的傳遞。綜合考慮熱阻及能耗等因素，將該塔的最佳操作壓縮比定為2.0。

符 號 說 明

Ad散熱面積，m2

Ai對應(yīng)傳熱位置的面積，m2

C，n公式系數(shù)

Csf組合常數(shù)

冷凝液的等壓熱容，J/（kg·K）

c水的比熱容，kJ/（kg·℃）

cp空氣的熱導(dǎo)率，kJ/（kg·℃）

d加保溫層后提餾段的直徑，m

di精餾段的塔內(nèi)徑，m

第一個極小極大值問題是文獻[4]中敘述的在分析一個二人紙牌博弈時得到的，當(dāng)時并未用到極小極大值術(shù)語。此后在1865年法國數(shù)學(xué)家德哈特在他的《概率的數(shù)學(xué)理論史》中曾提到過這個問題，但這在當(dāng)時并未引起概率論專家的注意。極小極大問題的解和思想，一直到1921年才又一次被著名的法國數(shù)學(xué)家波萊爾在研究零和博弈時發(fā)現(xiàn)。此后以美國數(shù)學(xué)家盧密斯的完全代數(shù)方法的極小極大值定理的證明為開端，在數(shù)學(xué)界發(fā)起了一場進一步證明極小極大值定理的運動，直到1928年馮諾依曼正式提出和證明了極小極大值定理，此后，這一定理的證明和求解方法又進一步得到了完善[5]。

Ga，K″ 無量綱數(shù)

g氣體常數(shù)，8.314 J/（mol·K）

ki對應(yīng)位置間的傳熱系數(shù)，W/（m2·K）

L換熱面的長度，m

Lp有效換熱長度，m

l塔高（不加封頭），m

m蒸汽冷凝水的質(zhì)量流量，kg/s

Pr普朗特數(shù)

Qi對應(yīng)位置間的傳熱量，kW

QReb傳統(tǒng)精餾塔再沸器的負(fù)荷，kW

QR′eb再沸器熱負(fù)荷，kW

QT兩塔段間的總傳熱量，kW

r水的汽化潛熱，kJ/kg

ΔT保溫層與環(huán)境之間的溫差，℃

tm定性溫度，℃

tI保溫層溫度，℃

tE環(huán)境溫度，℃

Δt精餾段與提餾段對應(yīng)位置上的溫差，℃

Δt′ 蒸汽的進出口溫差，℃

αf傳熱系數(shù)，W/（m2·℃）

αR冷凝對流給熱系數(shù)，W/（m2·K）

αS沸騰對流給熱系數(shù)，W/（m2·K）

β1/T，T為熱力學(xué)溫度（按理想氣體計算），K-1

δ精餾段厚度，m

λ空氣的導(dǎo)熱系數(shù)，W/（m·℃）

λw精餾段塔壁的導(dǎo)熱系數(shù)，W/（m2·K）

冷凝液的導(dǎo)熱系數(shù)，W/（m·K）

μ空氣的黏度，Pa·s

冷凝液的黏度，Pa·s

ρ空氣的密度，kg/m3

冷凝液的密度，kg/m3

飽和蒸汽的密度，kg/m3

σ氣-液界面的表面張力，N/m