考慮交通信息的PHEV電量消耗軌跡預測與跟隨算法研究
王 旭,杜光乾,黃 勇,田光宇
(清華大學 汽車安全與節能國家重點實驗室, 北京 100084)
由于現階段純電動汽車尚存在行駛里程短、電池價格高、使用壽命短、充電不方便等問題,因此發展插電式混合動力汽車(plug-in hybrid electric vehicle, PHEV)成為新能源汽車發展的重要組成部分[1-3]。從2011年到2016年,我國PHEV銷量從2 580輛增長至9.8萬輛, PHEV已表現出有效的節能減排能力。由于存在多個能量源且其最優工作區間不同,使得PHEV的性能與能量管理策略緊密相關。現有的策略主要是基于經驗制定的規則[4-5],其節能效果受工況的影響大,因此PHEV的燃油經濟性依然存在提升空間。隨著汽車智能化、網聯化成為必然趨勢,汽車部件及系統的控制策略可與多信息系統相結合[6]。若能將實時自車信息、道路信息以及交通信息等有效整合到PHEV的能量管理策略中,則可大幅提升PHEV的工況適應性,從而提升燃油經濟性。
根據能量管理策略是否以建立數學模型為基礎,PHEV的策略可以分為基于規則和基于優化兩種[1,7-9]。基于規則的策略通常根據工程師的經驗制定,根據其規則是否以模糊數學為基礎,可以分為確定規則的策略和模糊規則的策略[5,10-13]。基于優化的策略則需要建立數學模型,利用優化方法進行求解,主要有基于極小值原理的策略[14-15]和基于動態規劃(dynamic programming, DP)的策略[16-17]。DP算法將復雜問題分解為簡單子問題并層層求解,是解決復雜優化問題的常見方法之一[16]。Brahma等[18]在給定工況上運用DP算法求解了串聯混合動力汽車的能量管理問題。針對DP算法需要工況已知和計算量大的問題,Gong等[19]結合ITS系統提出了雙尺度的DP算法,與傳統的DP算法相比增加了在線應用能力,并且提升了3.7%的燃油經濟性。
本文旨在利用ITS提供的多種信息設計PHEV的能量管理策略。由于目前ITS尚未完全普及,因此有必要首先搭建能獲得自車、交通、道路數據的駕駛員在環仿真平臺,從而為算法的研究提供基礎。在研究電池電量消耗與交通擁堵等級的關系時發現二者顯著相關,因此可依據交通擁堵等級預測電量消耗軌跡。首先在剩余行程的尺度上利用各路段的交通擁堵等級預測車速,通過DP算法求解得到各路段的可用電量;然后在當前路段的尺度上利用多種信息更準確地預測車速,并結合該路段的可用電量求解得到最優電量消耗軌跡;最后通過算法跟隨該軌跡從而實現在線控制,并驗證了算法的有效性。
1 獲取ITS數據的仿真平臺
由于難以獲得現實中ITS的各信息,本文在清華大學汽車安全與節能國家重點實驗室的模擬駕駛實驗系統的基礎上搭建了仿真環境進行駕駛員在環仿真實驗,以期獲得自車數據、交通數據和道路數據等,以便開展基于ITS的能量管理算法研究。
1.1 仿真環境
為了盡量還原真實的駕駛場景,需要搭建仿真道路環境和交通環境。前者包括道路、路口、交通指示燈以及路邊景觀等,本文定義了23個平均長度為3 km的路段,共22個路口。后者指行車隊列中各車的運行方式,主要包括頭車和跟車的車速和安全距離模型。行車隊列如圖1所示。
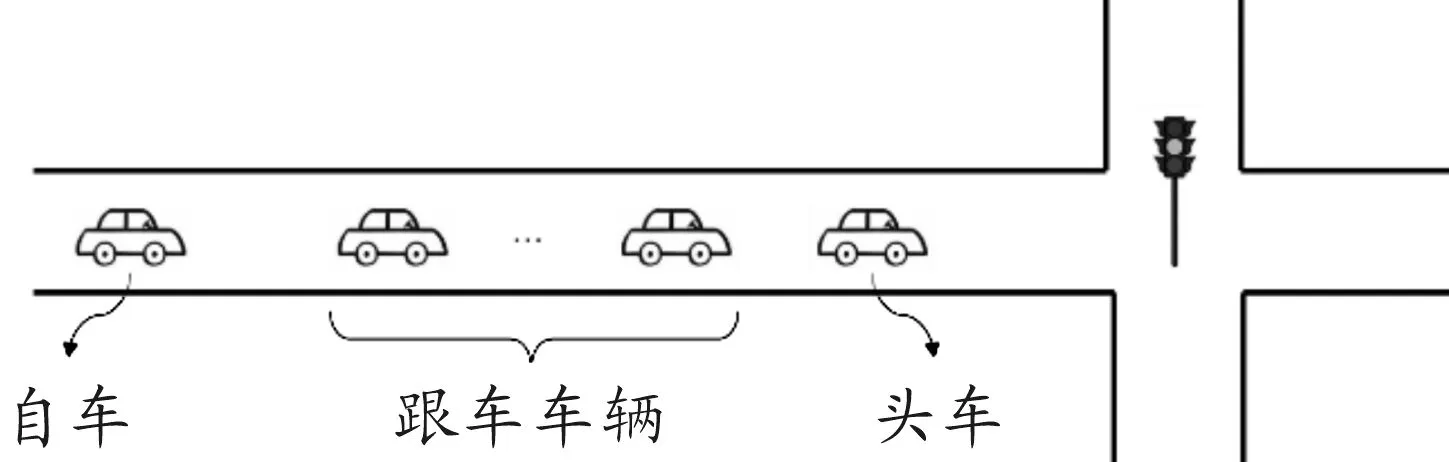
圖1 行車隊列示意圖
1.2 仿真實驗
基于上述駕駛模擬系統和仿真環境,本文設計了7條具有不同交通環境的路線并進行了駕駛員在環仿真實驗,獲得了對應的7組實驗數據,其中每組數據包括圖2中的8個信號。以下的策略研究將以該7組數據為研究基礎。
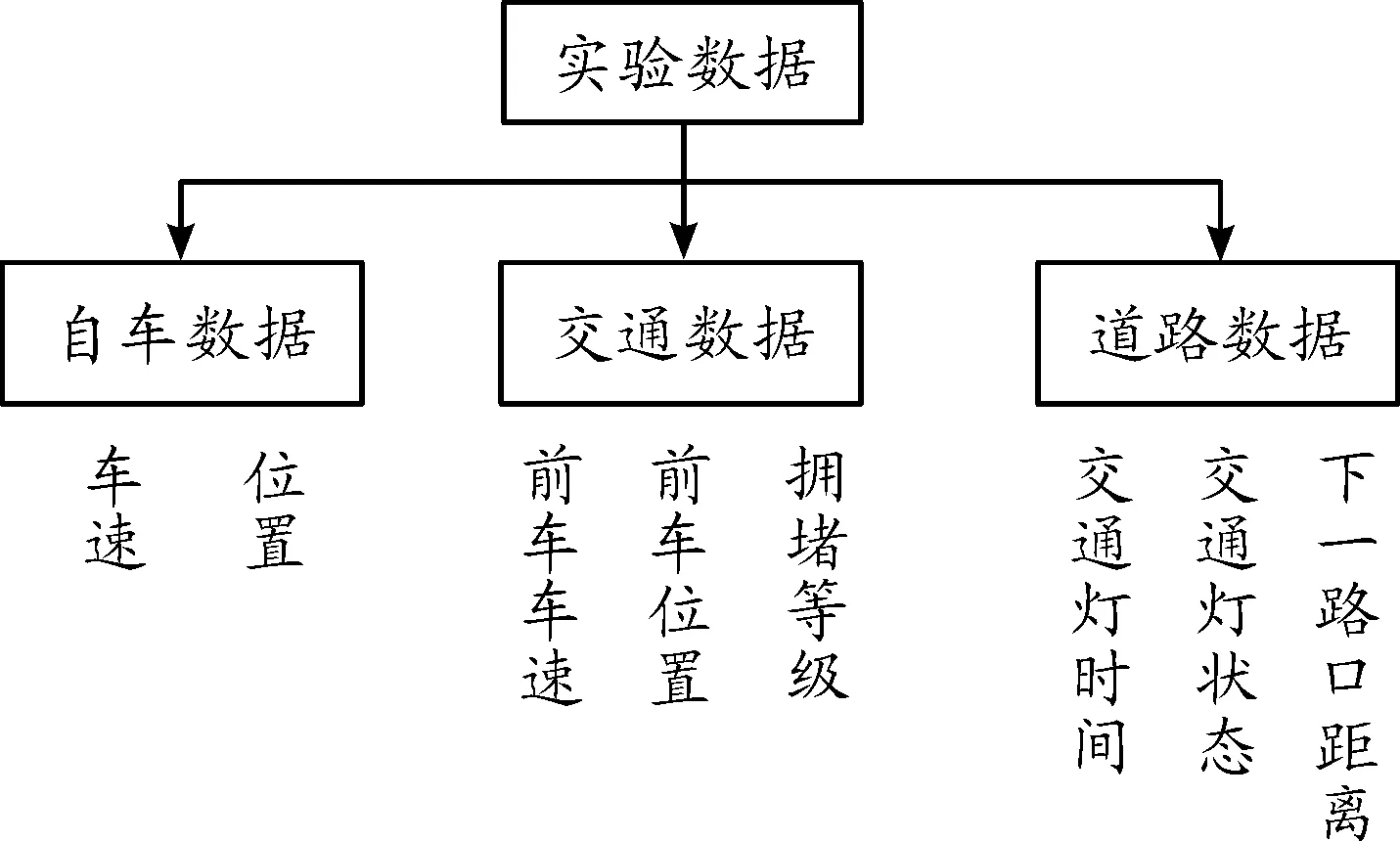
圖2 實驗中采集的數據
圖2中的交通擁堵等級的定義參照北京市交通擁堵評價體系,如表1所示,共分為5個等級,即通過計算各路段的平均車速獲得其交通擁堵等級。

表1 交通擁堵等級定義
2 問題建模與求解
本文所研究的并聯式PHEV的動力系統結構簡圖如圖3所示,其工作模式包括發動機模式、純電模式、混動模式和制動能量回收模式。為設計基于ITS的在線策略,可先利用DP算法求解全局最優解并探索規律,再設計在線自適應策略。
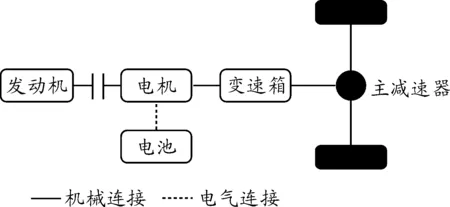
圖3 并聯式PHEV動力系統結構簡圖
2.1 能量優化問題模型
本文選取動力電池組的SOC作為狀態量,驅動電機輸出功率Pm(t)作為控制變量。能量優化問題的目標函數如式(1)所示。
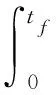
(1)
其中:poil表示油價;Coil表示發動機的燃油消耗速率(L/h),主要依據發動機萬有特性圖獲得;pele表示電價;Cele=VocIb表示動力電池的耗電功率,Ib(t)為電池電流。由Rint模型有:
(2)
其中:Pb(t)為電池輸出功率;Voc(t)為電池的開路電壓;R(t)為電池內阻。根據SOC的定義可得其變化率為式(3)所示,其中Qb是電池的標稱容量。
式(1)所示的優化問題存在的約束條件包括:始末點狀態量確定的等式約束、過程中控制量和狀態量因物理原因導致的不等式約束,且存在等式約束,如式(4)所示,其中Pbus為整車需求功率,Pengine為發動機的輸出功率。
Pbus(t)=Pengine(t)+Pm(t)
(4)
2.2 動態規劃求解
DP將復雜問題分解為簡單子問題并層層求解,是解決復雜優化問題的常見方法之一。由于上述能量優化問題高度非線性,難以解析求解,但可數值求解。將式(1)改寫為:
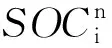
通過正向求解可以得到原問題的最優解,其求解過程如圖5所示。
對實驗所獲得的7個線路的數據采用DP算法得到其最優SOC變化軌跡,其中線路1的最優SOC變化軌跡如圖6所示。
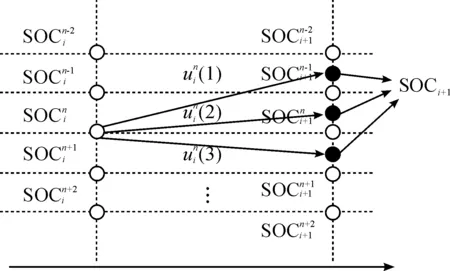
圖4 動態規劃倒序求解示意圖
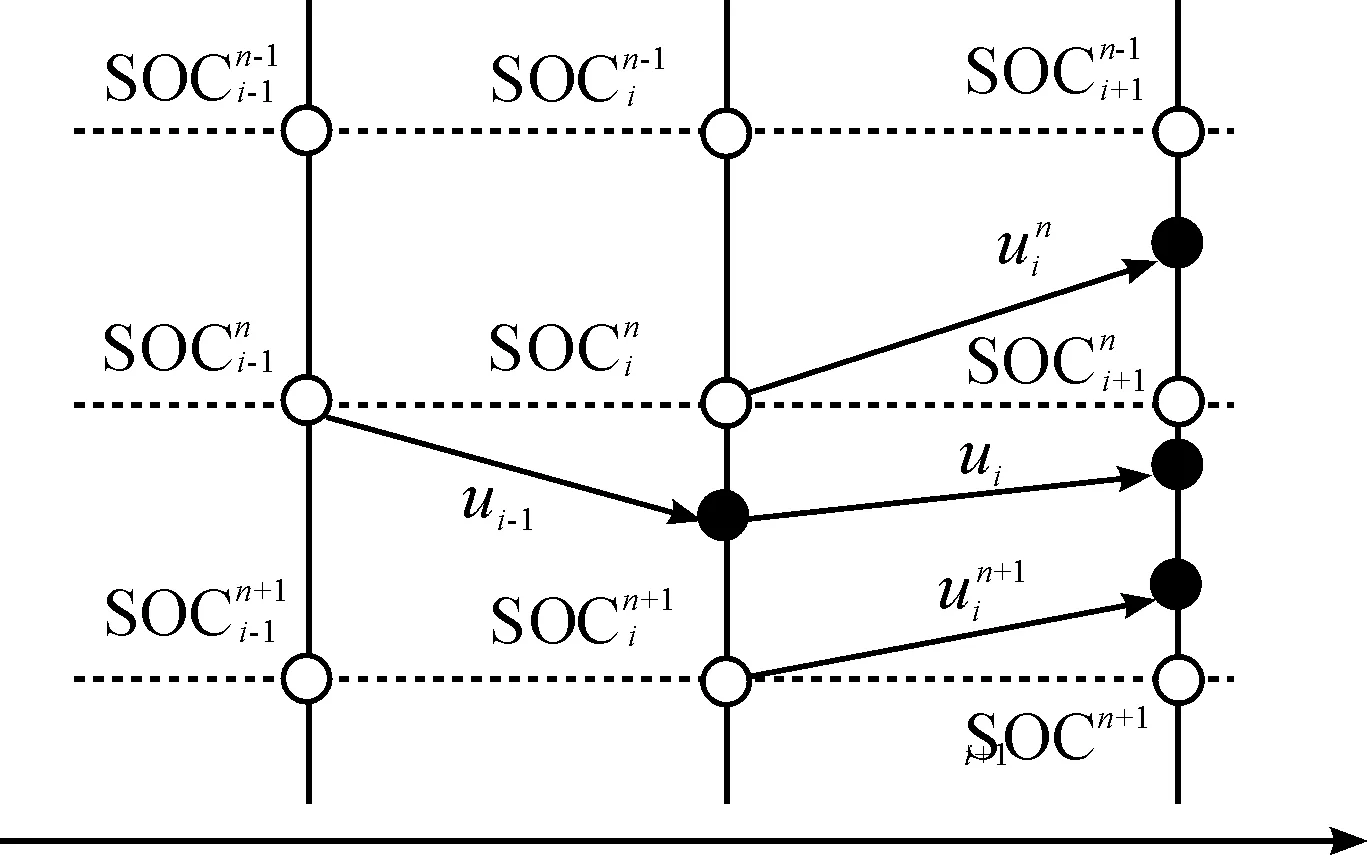
圖5 動態規劃正向求解示意圖
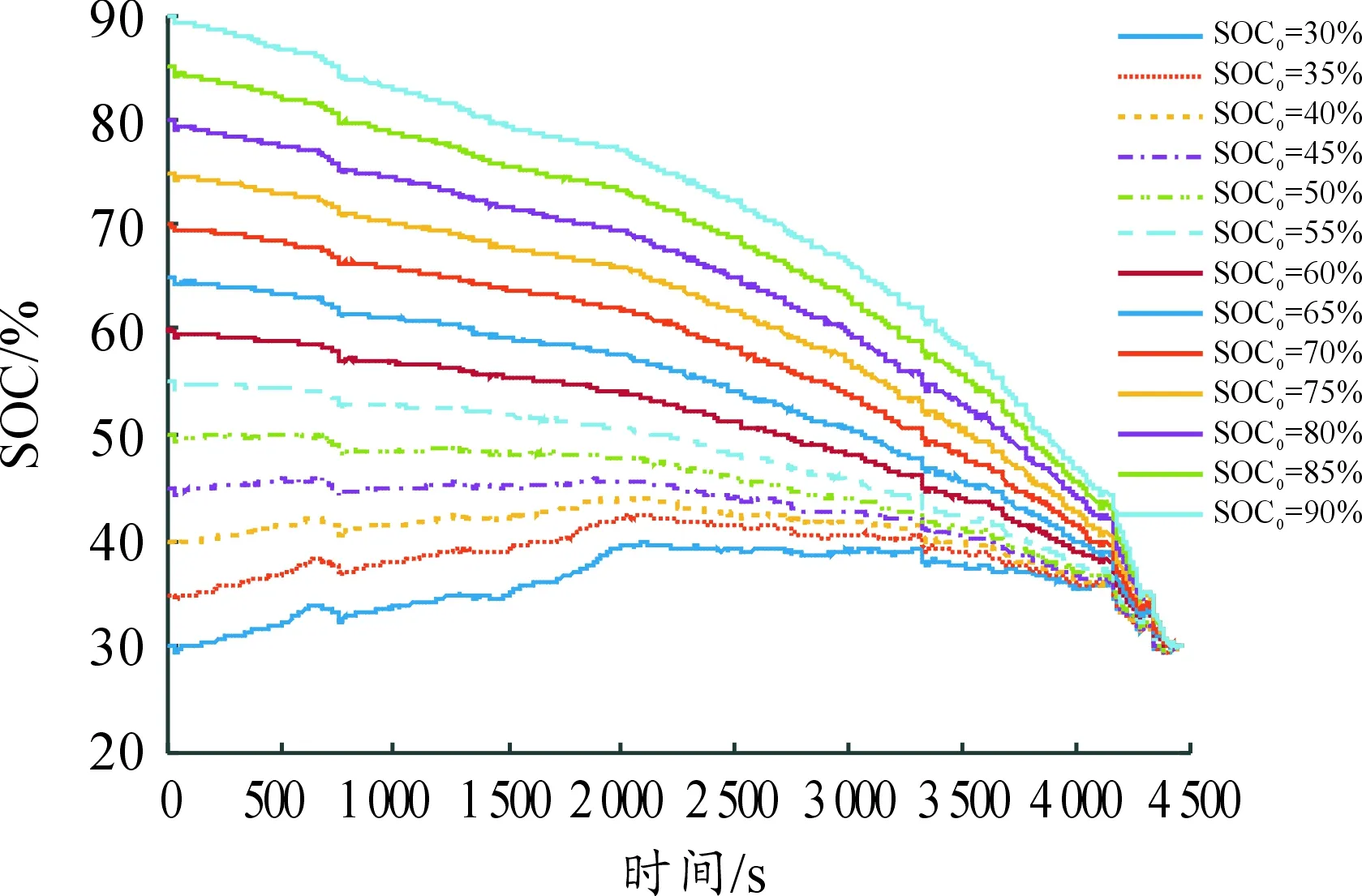
圖6 線路1的最優SOC變化軌跡
在利用箱線圖定性分析各初始SOC下的電池電量變化速率與交通擁堵等級的關系時發現二者顯著相關,以SOC0=0.9時的結果為例,如圖7所示,交通擁堵等級越高,即平均車速越大,電池電量變化速率越大。再利用Spearman相關系數定量研究不同初始SOC下二者的相關性,發現相關系數均在0.612 7~0.710 7之間,進一步表明電池電量變化與交通擁堵等級之間的相關性。
3 多信息電量消耗軌跡預測算法
雖然電池電量變化與交通擁堵等級之間存在相關性,但直接根據交通擁堵等級預測電量消耗軌跡難以收斂,而車速序列是判斷交通擁堵等級的依據,也是獲得電量消耗軌跡的來源。因此,本文一方面利用剩余行程各路段的交通擁堵等級預測對應路段的車速,然后利用DP算法求解出剩余行程的最優電量消耗軌跡,從而得到各路段的可用電量。另一方面,利用當前路段的可用電量和多種實時信息可更準確地預測出當前路段的車速,并利用DP算法求解出當前路段的電量消耗軌跡,在線控制時則跟隨該軌跡。在訓練上述2個車速預測模型時,利用從仿真平臺上采集的前6條線路的數據,將第7組數據用于驗證算法的有效性。
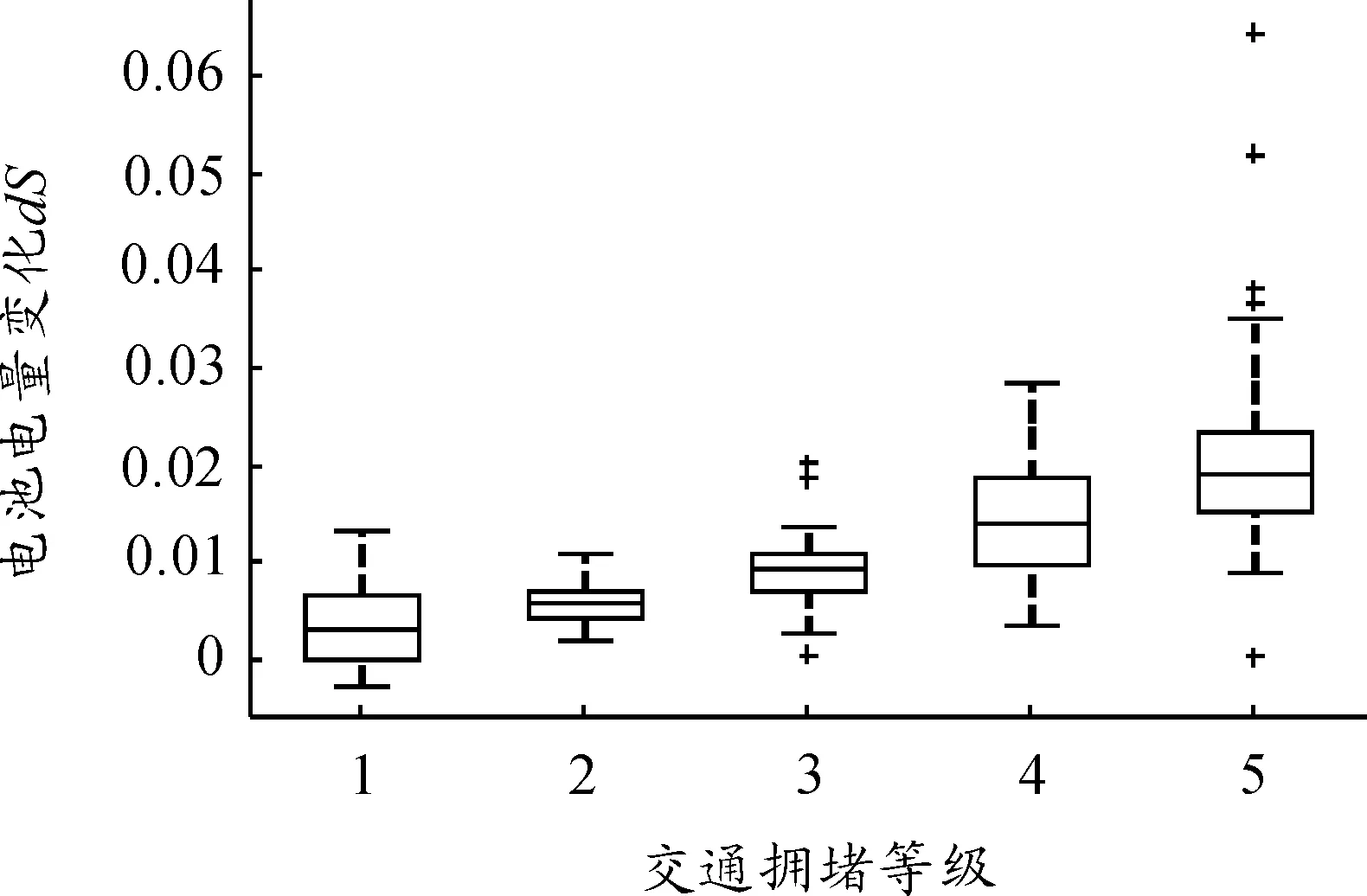
圖7 SOC0=0.9時電池電量變化與交通擁堵等級關系
3.1 剩余行程電量分配算法
為了預測剩余行程的車速序列以分配各路段的電池電量,本文設計的復合NARX網絡模型如圖8所示,其由3個NARX網絡模型構成。相對于單NARX網絡模型,該復合模型在長時間預測時不會產生振蕩。
由于在根據各路段的交通擁堵等級預測車速時并沒有在線的前幾秒車速可以利用,因此本文隨機選取該交通擁堵等級下的歷史工況片段的初始5 s車速作為初始數據,然后輸入至第1個NARX網絡模型中以預測其后的30 s的車速。然后,將此刻已有的35 s車速輸入到第2個NARX網絡模型中,從而預測此后20 s的車速。第3個NARX網絡模型則以此前的55 s的車速為輸入,預測當前路段剩余里程的車速序列。
通過從前6組仿真數據中提取的各交通擁堵等級下的工況數據,訓練上述復合NARX網絡模型,得到了與不同交通擁堵等級相對應的復合車速預測模型。在線應用時則先從ITS中獲取各路段的擁堵等級,然后利用對應的車速預測模型預測各路段的車速序列,并組成剩余行程的車速序列,最后利用DP算法計算出電量消耗軌跡,從而獲得各路段的電量分配結果。
為了研究通過上述剩余行程電量分配算法分配電池電量的效果,對比了所預測的工況和采集的第7組工況所對應的全局最優SOC軌跡,結果如圖9所示,二者的變化趨勢幾乎一致,但預測工況對應的SOC軌跡存在累積誤差,表明僅依據交通擁堵等級可以獲得良好的全程電量分配結果。

圖8 復合NARX網絡模型
雖然通過上述電量分配算法實現了良好的全程電量分配,但當車輛行駛在當前路段時,可進一步利用更多的實時信息,如前車車速、跟車距離、交通燈狀態及自車歷史車速等,以提高當前路段上車速預測的準確性。
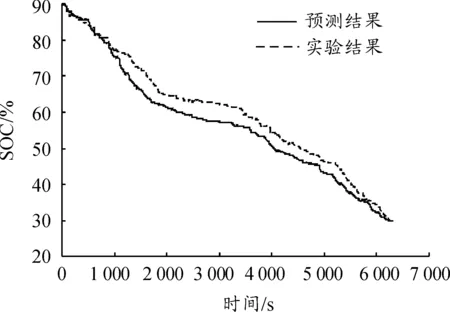
圖9 預測工況與實驗工況最優SOC變化對比
3.2 當前路段電量消耗軌跡預測算法
針對當前路段上不同階段的特點,本文設計了3階段車速預測算法,一方面避免了預測時長有限的問題,另一方面充分結合了不同階段的特點,算法結構如圖10所示。
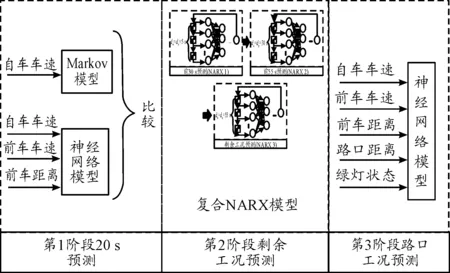
圖10 3階段區間路段車速預測算法
當車輛行駛在當前路段上時,其自車車速、自車位置、前車車速和前車距離均會影響未來短時間的車速。利用這些信息作為未來20 s車速預測神經網絡模型的輸入,得到了比只以自車車速為依據的Markov模型更好的車速預測結果,該神經網絡模型的預測結果如圖11所示。
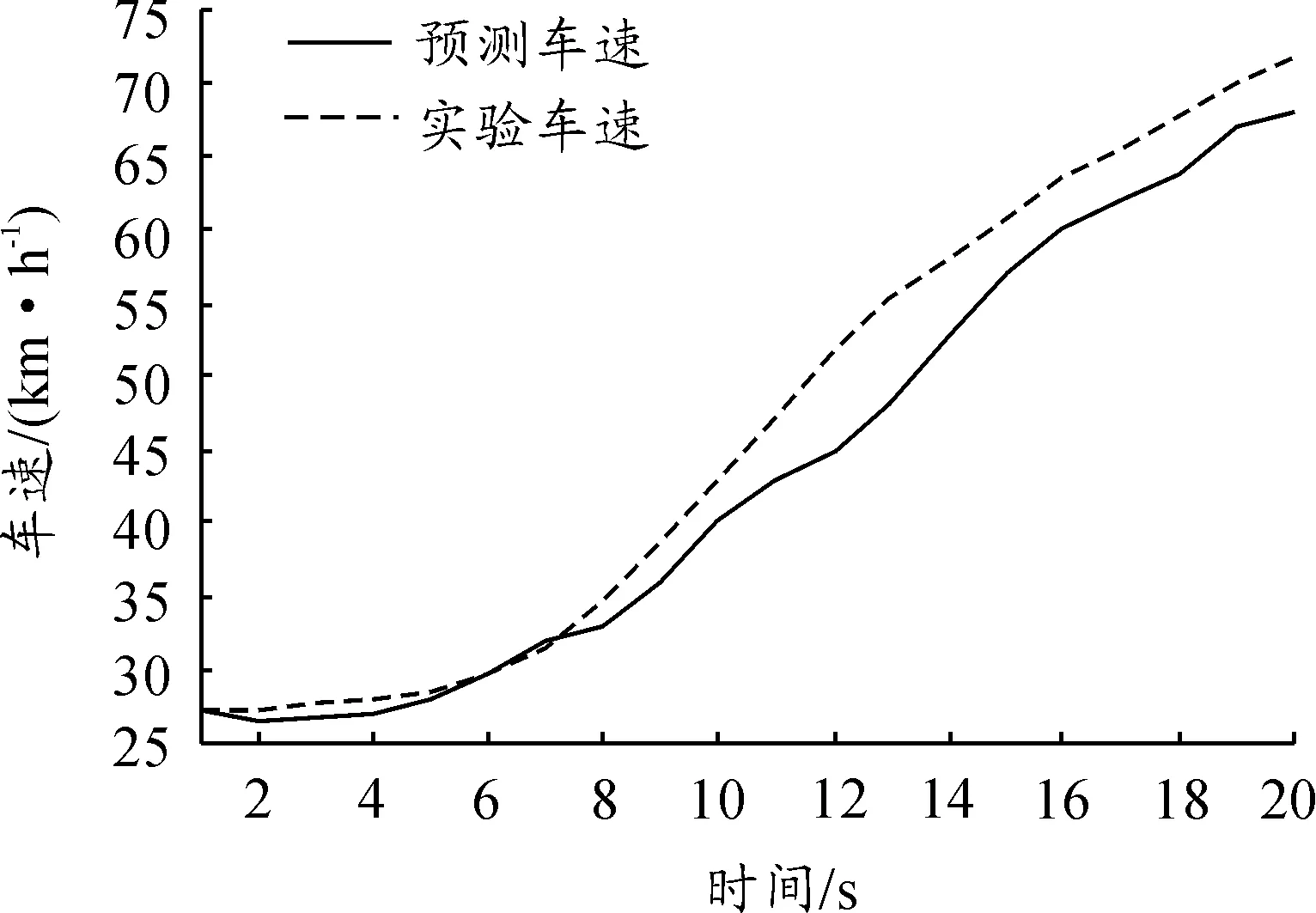
圖11 第1階段神經網絡模型預測結果
以第1階段神經網絡模型預測的20 s車速為輸入,利用本文3.1節中的復合NARX網絡模型作為第2階段的車速預測模型。圖12展示了分階段的車速預測與不分階段的車速預測(僅復合NARX模型預測)的結果對比,可以看出:基于上述2個階段的車速預測模型的預測結果與實驗結果相當,同時優于無第1階段的模型。
第3階段由于接近路口,因此在第1階段輸入參數的基礎上增加了與路口距離及交通燈狀態2個輸入,建立了神經網絡模型。對比采用第1階段和第3階段模型進行車速預測的結果,發現新增的2個輸入在車輛接近路口時能明顯地改善車速預測效果,結果如圖13所示。
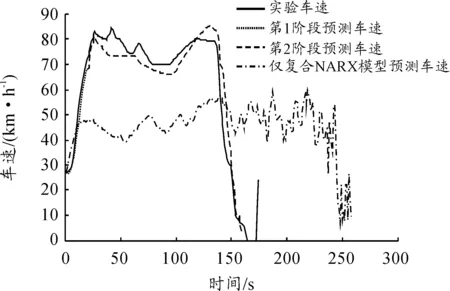
圖12 第2階段復合NARX網絡模型預測結果

圖13 第3階段神經網絡模型預測結果
由于融合了更多實時交通信息和道路信息,上述3階段區間路段車速預測算法比圖8中的復合NARX網絡模型在區間路段上預測的車速更加接近實驗數據。由于預測出了當前路段的車速序列,且由本文3.1節中的剩余行程電量分配算法可以得到當前路段結束時的SOC,因此可以再次利用DP算法得到當前路段的最優SOC軌跡,并以此作為參考曲線用于設計在線能量管理策略。
4 電量消耗軌跡跟隨算法
4.1 算法介紹
在計算最優電量消耗軌跡的過程中,本文未研究DP的運算復雜度,在線應用時可以考慮借助云計算平臺完成上述計算任務。由于交通擁堵等級的變化較慢,因此在實施本文3.1節所描述的剩余行程電量分配算法時可每隔2個路段計算1次。本文3.2節中的分3個階段的當前路段電量消耗軌跡預測需要更高的實時性,因此可以每隔15 s實施一次。
由本文第3節可獲得最優電量消耗軌跡,在線能量管理策略則可依據實際SOC與該曲線的偏離情況和整車需求功率的大小決定動力系統的工作模式和功率分配。當實際SOC大于參考的SOC一定值時,可以在滿足需求功率的條件下盡量多耗電。當實際SOC小于參考的SOC一定值時,可以在滿足需求功率的條件下發電且保證發動機工作在高效區間內。
4.2 算法性能分析
利用線路7的數據驗證所設計的電量消耗軌跡跟隨算法的性能,以SOC0=0.9為例,對比離線DP得到的最優電量消耗軌跡、預測出的電量消耗軌跡、在線電量消耗軌跡跟隨算法的結果及CDCS策略的電量消耗軌跡,如圖14所示,表明跟隨算法與最優電量消耗軌跡相近。
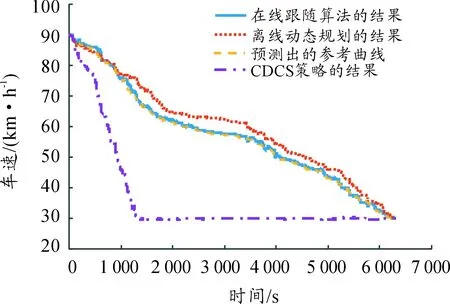
圖14 SOC0=0.9時多種策略SOC軌跡比較
利用線路7的數據,對比不同SOC0下各算法的油耗,計算出DP算法與本文提出的跟隨算法相對CDCS策略的節油率,如表2所示。
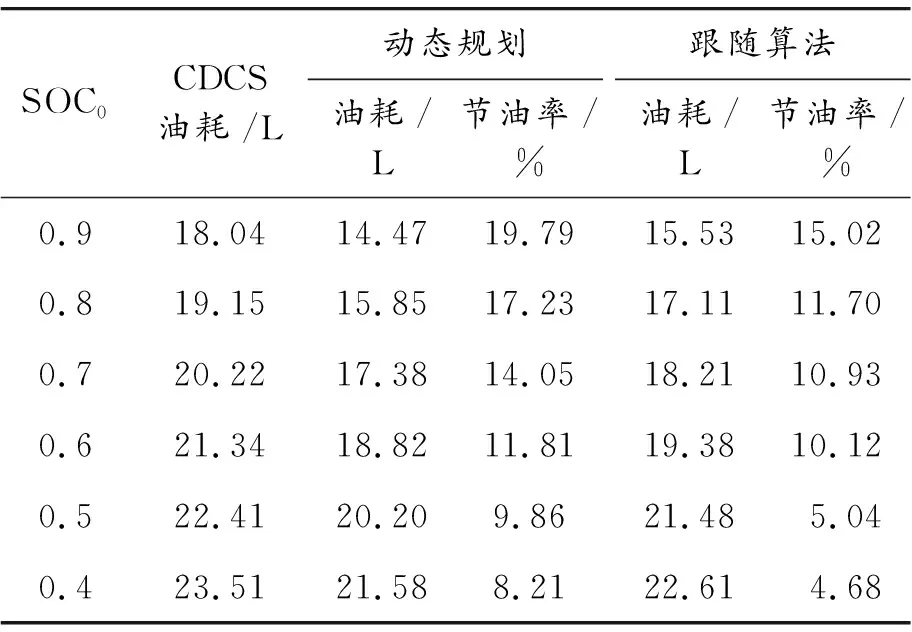
表2 不同算法和SOC0下的油耗計算結果
從表2可以看出:本文所提出的基于ITS的電量消耗軌跡跟隨算法相對于CDCS策略能穩定地降低油耗,且與動態規劃得到的最優解相近。
5 結論
本文設計了考慮多種交通信息的插電式混合動力汽車電量消耗軌跡預測與跟隨算法,即首先利用各路段的道路擁堵等級進行車速預測并獲得各路段的電量分配結果,然后在當前路段的尺度上利用更多信息進行車速預測,并結合路段可用電量得到參考SOC軌跡。在線應用時則以實際SOC值與參考SOC值的偏差進行反饋調節,使得車輛的真實SOC軌跡跟隨參考軌跡。基于該電量消耗軌跡預測與跟隨算法,仿真得出相比于CDCS策略其節油率最多可達15.02%,并接近動態規劃算法的全局最優解。

