基于Star-ccm+的某水冷電機控制器熱仿真及分析

賴晨光，呂 寶，陳 祎，胡 博

(重慶理工大學 汽車零部件先進制造技術教育部重點實驗室， 重慶 400054)

隨著再生能源的日益枯竭和排放規定的限制，開發新能源汽車已是大勢所趨。電動汽車的電機控制器中的IGBT模塊作為驅動系統中的關鍵部件其散熱性能直接影響電機的輸出性能及電驅動系統運行的可靠性，電機的頻繁啟動和關閉會使IGBT功率模塊產生大量的熱，若不能及時把熱量傳遞出去將會造成IGBT被擊穿，控制器被燒毀，嚴重影響了控制器的質量和可靠性[1]。目前，常用電機控制器的冷卻方式為水冷和自然風冷。風冷散熱效果遠低于水冷，對于高功率控制器來說更是如此。控制器的散熱元件主要有風冷散熱器[2]、冷板散熱器[3]、熱管散熱器[4-5]等，目前大多數學者只針對控制器中的IGBT模塊進行仿真分析，對冷卻系統的改進較少，因此本文針對控制器水道內的不同高度、不同形狀的擾流塊對水流均勻性、壓降及IGBT溫度產生的影響進行研究，得到了擾流塊不同高度及形狀之間的規律，為前期開發和優化提供參考。

1 控制器功率模塊傳熱分析

電機控制器的主要發熱部件為IGBT模塊，其結構布置如圖1所示。在IGBT下方除了導熱硅膠和鋁基板外設置了1個1 mm深的冷卻水槽，其下方為電容模塊。冷卻水槽直接和鋁基板進行對流傳熱，而IGBT的熱量是通過熱傳導將熱量傳遞給導熱硅膠再經鋁基板被冷卻介質帶走。冷卻水槽內加裝有擾流塊，其目的為：一是破壞固體表面的邊界層，增加冷卻液的湍動能以帶走更多的熱量；二是使水流更加均勻地分布以增加散熱均勻性。根據傳熱學第二定律，在有溫度差異時，熱能會從溫度高的地方自發地傳遞到溫度低的地方[6]。傳熱方式分為3種：熱傳導、熱對流、熱輻射，其導熱規律由傅里葉定律給出[7]。熱傳導表達式為

Q=-λΑdt/dx

(1)

式中： Q為熱傳導熱流量; λ為材料導熱系數; A為垂直于導熱方向的截面積;dt/dx為溫度t在x方向的變化率。冷卻水道和鋁基板之間的換熱為對流換熱，對流換熱可用牛頓冷卻公式表達：

Q=-αAΔt

(2)

式中：Q為對流換熱量;α為對流換熱系數;A為有效對流換熱面積; Δt為固體表面與冷卻液之間的溫差。

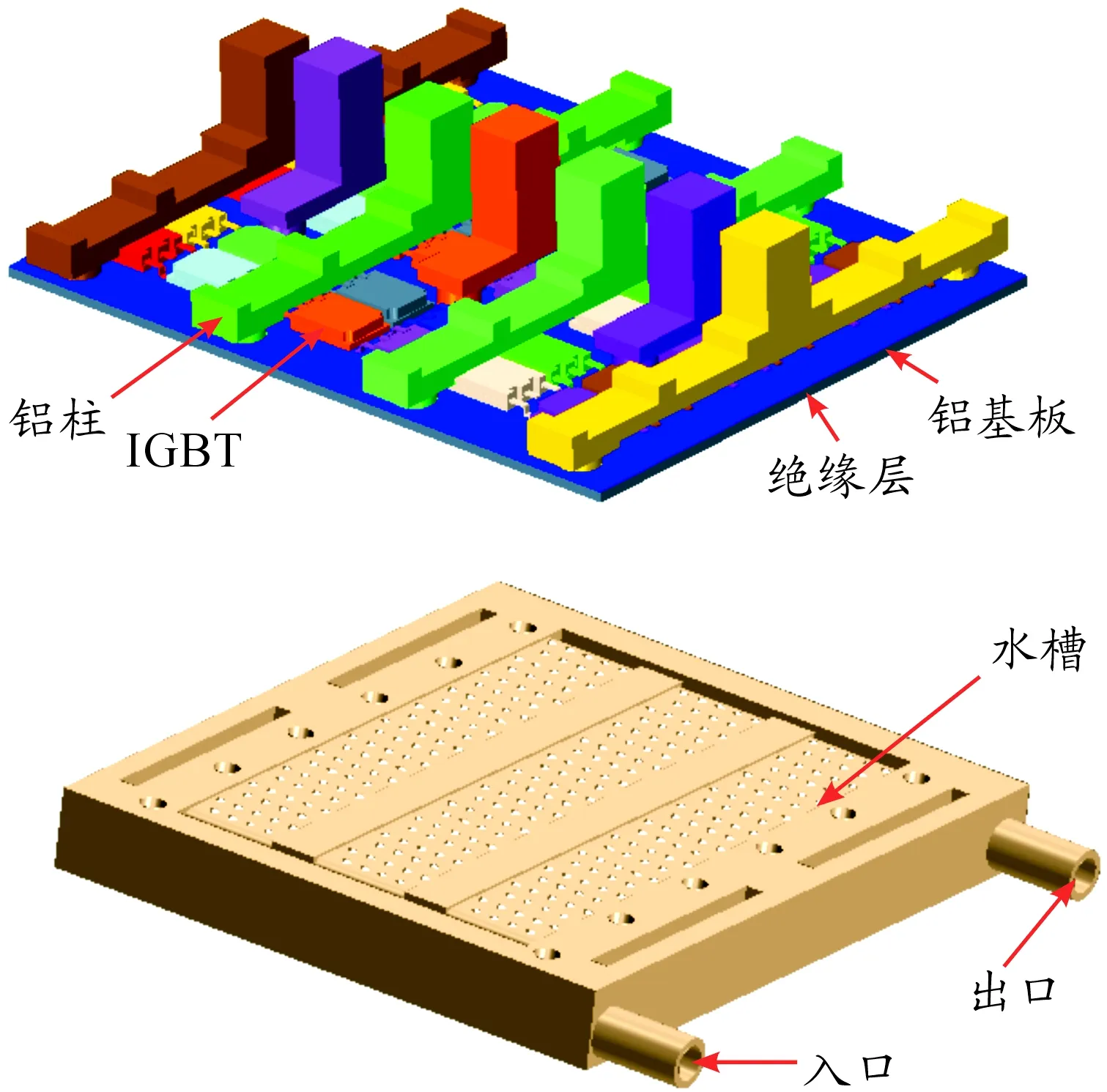
圖1 控制器內部結構分布

2 幾何建模及網格劃分

2.1 幾何模型建立

通過三維軟件CATIA建立了本文所研究的模型，如圖2所示。該控制器由水道、鋁基板、絕緣層、IGBT、鋁柱(正負極和三相線板)、外殼、底板等組成，絕緣層的厚度為0.4 mm。為防止水流直接沖擊內流道造成能量損失，在入口處進行拔模減緩水流的沖擊。水道內的擾流塊由正方形、菱形、圓臺、平鋪4種方式組成，并按照4、5、4、5方式進行排列，如圖3所示。

圖2 幾何模型

圖3 擾流塊排列方式

2.2 網格劃分

由于該控制器模型尺寸較小，故在進行面網格操作時采用“三角形+四邊形” 網格策略，使其更貼合以避免失真。控制器外殼網格尺寸設為8 mm，內部部件IGBT、鋁基板及鋁柱網格尺寸設為2 mm，絕緣層和擾流塊網格尺寸為0.2 mm。體網格采用切割體網格策略，最終生成68.5萬個面網格、48萬個體網格。

2.3 網格無關性驗證

在穩態計算過程中為消除網格質量和數量對計算結果帶來的誤差，需進行網格無關性驗證[8]。本文采用相同質量的4種不同網格尺寸對控制器進行仿真計算，結果如表1所示。隨著網格數的增加，IGBT的溫度差值最大為0.127 ℃，誤差為0.15%，管道總壓降最大差值為961 Pa，誤差為2.51%。水道內各個支口的質量流量也是檢驗網格無關性的重要參數。如圖4～6所示，通過不同網格尺寸計算出的支口速度幅值變化較小，且3個支道進口面積相同，最大誤差為2.8%，三者最大誤差都小于仿真允許誤差5%，滿足網格無關性要求。考慮仿真精度和計算時間成本，選取網格數為48萬的網格進行計算。

表1 網格無關性驗證

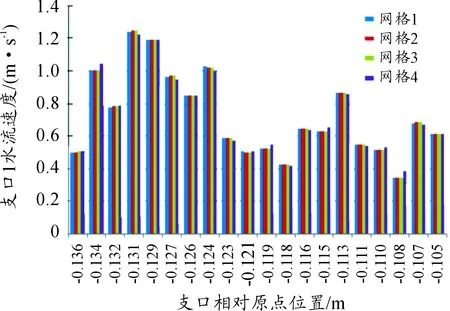
圖4 水道A支口速度分布

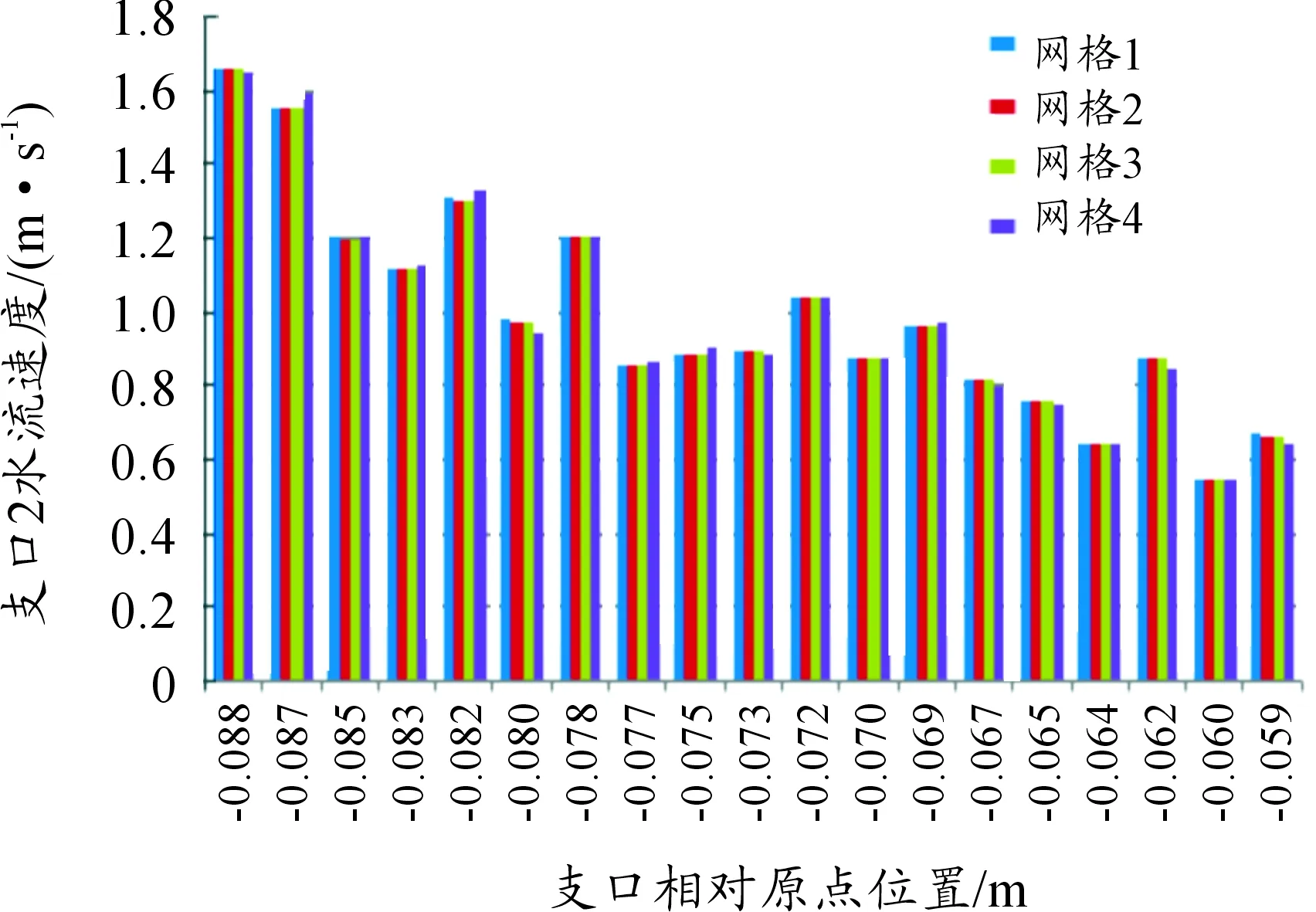
圖5 水道B支口速度分布

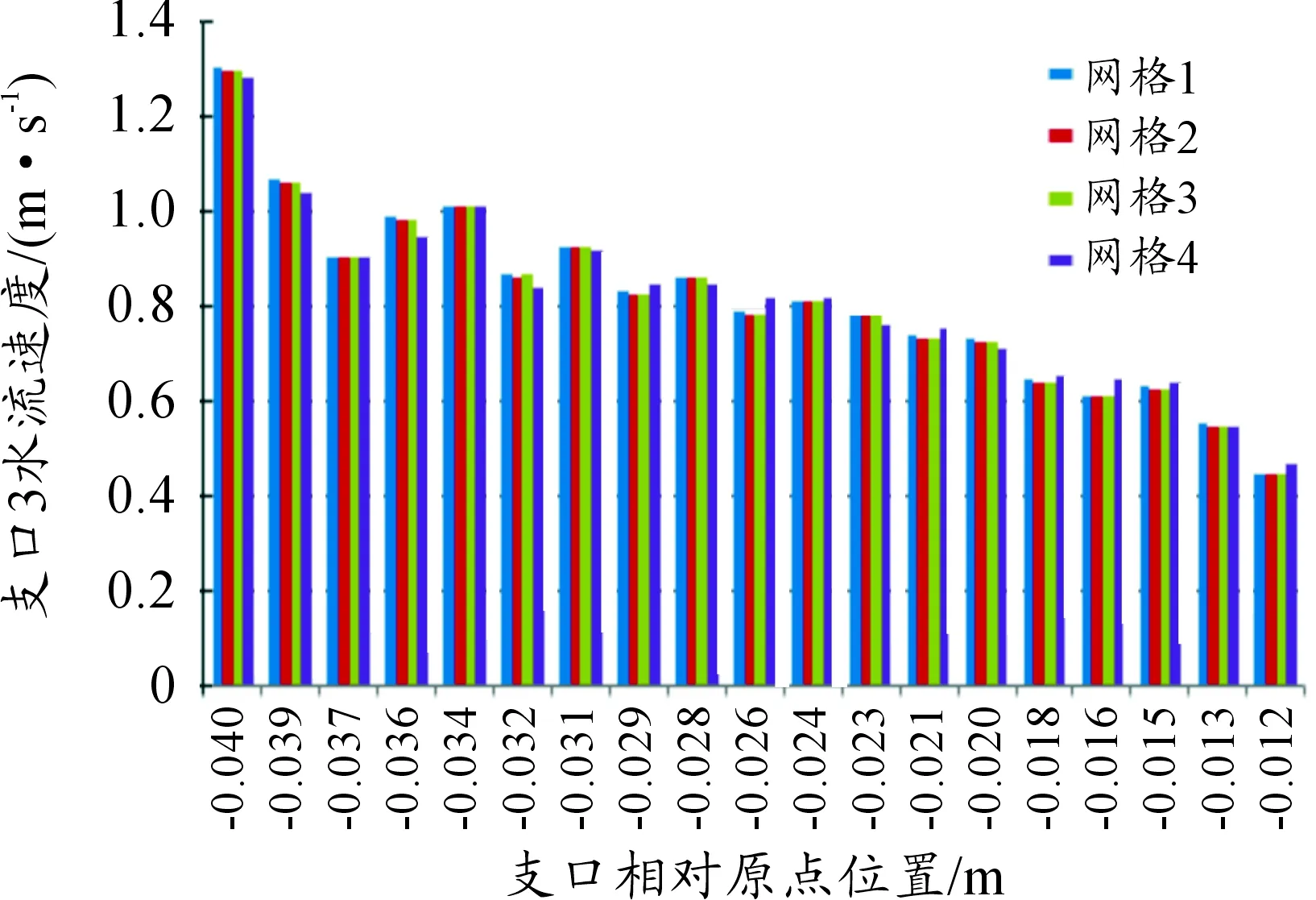
圖6 水道C支口速度分布

3 數值計算及分析

3.1 邊界條件及求解器設置

本研究選取穩態計算的數值模擬方法。IGBT單個熱功率為53.5 W，共36個，冷卻液采用50%乙二醇，絕緣層采用導熱系數較高的絕緣橡膠，其余部件采用壓鑄鋁，各部件材料屬性見表2。初始溫度為50 ℃，入口設置為質量流量進口，大小為0.176 kg/s；出口設置為壓力出口，相對壓力設置為0 Pa；流場的湍流模型選用可實現的k-ε湍流模型，流場求解器基于couple算法，開啟能量方程和重力場。

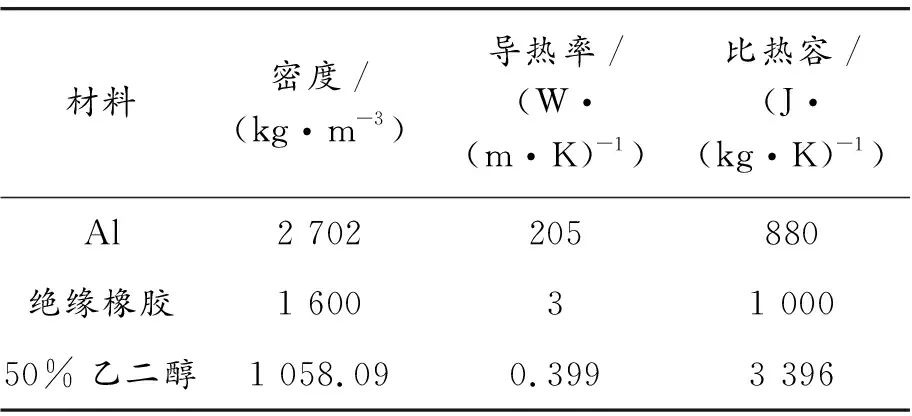
表2 材料屬性

3.2 仿真結果分析

本次仿真模型選取高度為0.7 mm的正方形擾流塊，通過Star-ccm+軟件自帶的后處理器，求得溫度場和流場的分布情況。圖7為整個控制器的溫度場云圖，從標尺可以看出最高溫度為79.826 ℃，最大溫升為29.826 ℃，溫度分布梯度較為明顯地沿y軸方向依次增大，出入口溫度溫差為2.8 ℃，最高溫度出現在主要熱源IGBT上。如圖8所示，沿y軸第3排的IGBT平均溫度高達78 ℃，主要由于其排列較為緊密導致溫升變大，沿x負半軸方向溫度依次升高是由于水道截面變小使得第3列IGBT的溫度較高。絕緣層靠近出口處溫度為52.357 ℃，接近初始溫度，其最大溫升為25 ℃，貼合IGBT處溫度最高的情況，如圖9所示。圖10為速度矢量圖，最大速度為3.47 m/s，出現在入口處。由于擾流塊的作用使得流道內的水流產生局部加速，能帶走更多的熱量，并且3個支道的水流分布較為均勻，避免了功率器件局部過熱的發生。流道壓力呈順壓梯度分布，隨著動能的變化壓力損失逐漸變大，在支道出入口冷卻液速度的變化是由于橫截面的改變導致其壓力波動較大，出入口處總壓降為 30 759.7 Pa，如圖11所示。從水道流線圖12可看出：水流無斷流產生，冷卻液都能夠順利通過水道，冷卻液在出口處呈螺旋狀流出。這主要是由于勢能的增加和液體沖擊水道壁面造成流體改變方向發生旋轉，便于冷卻液流出水道。

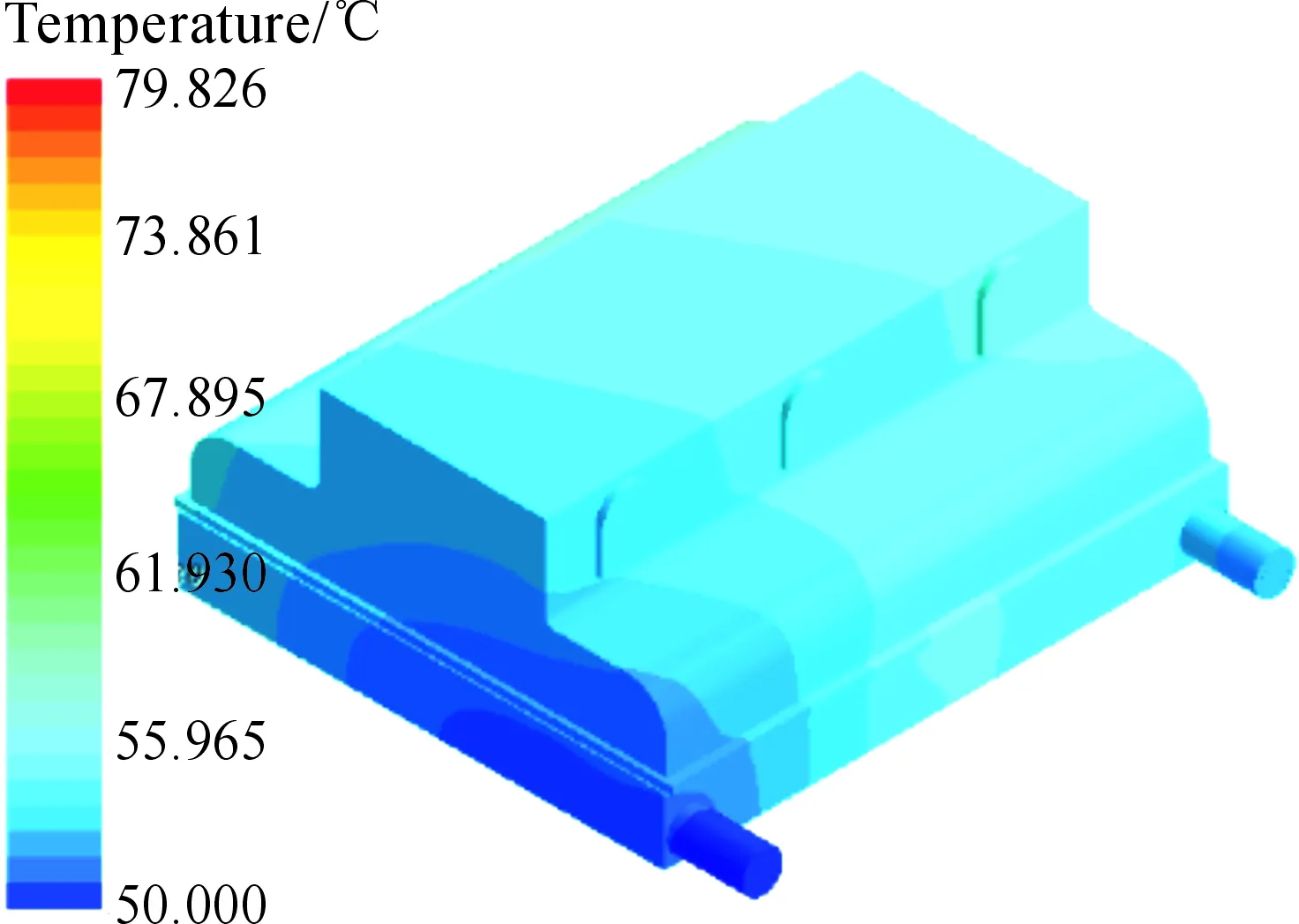
圖7 控制器溫度云圖

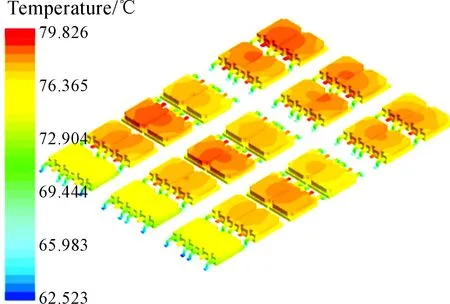
圖8 IGBT溫度云圖

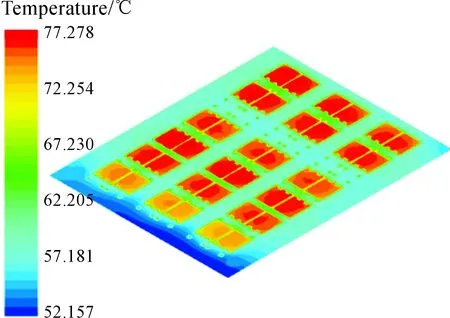
圖9 絕緣層溫度云圖

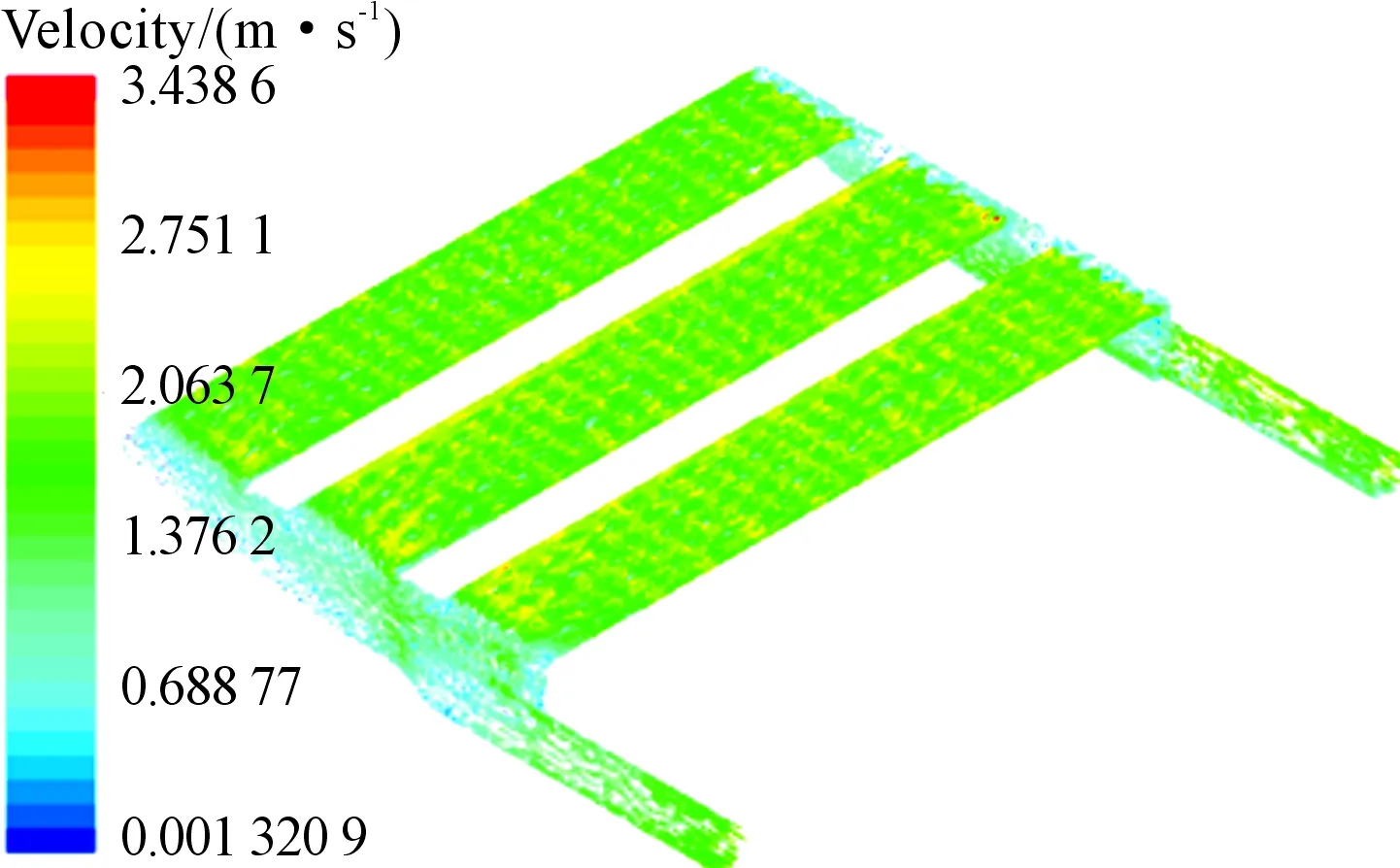
圖10 水道速度云圖

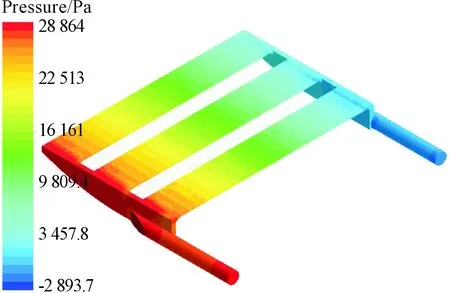
圖11 水道壓力云圖

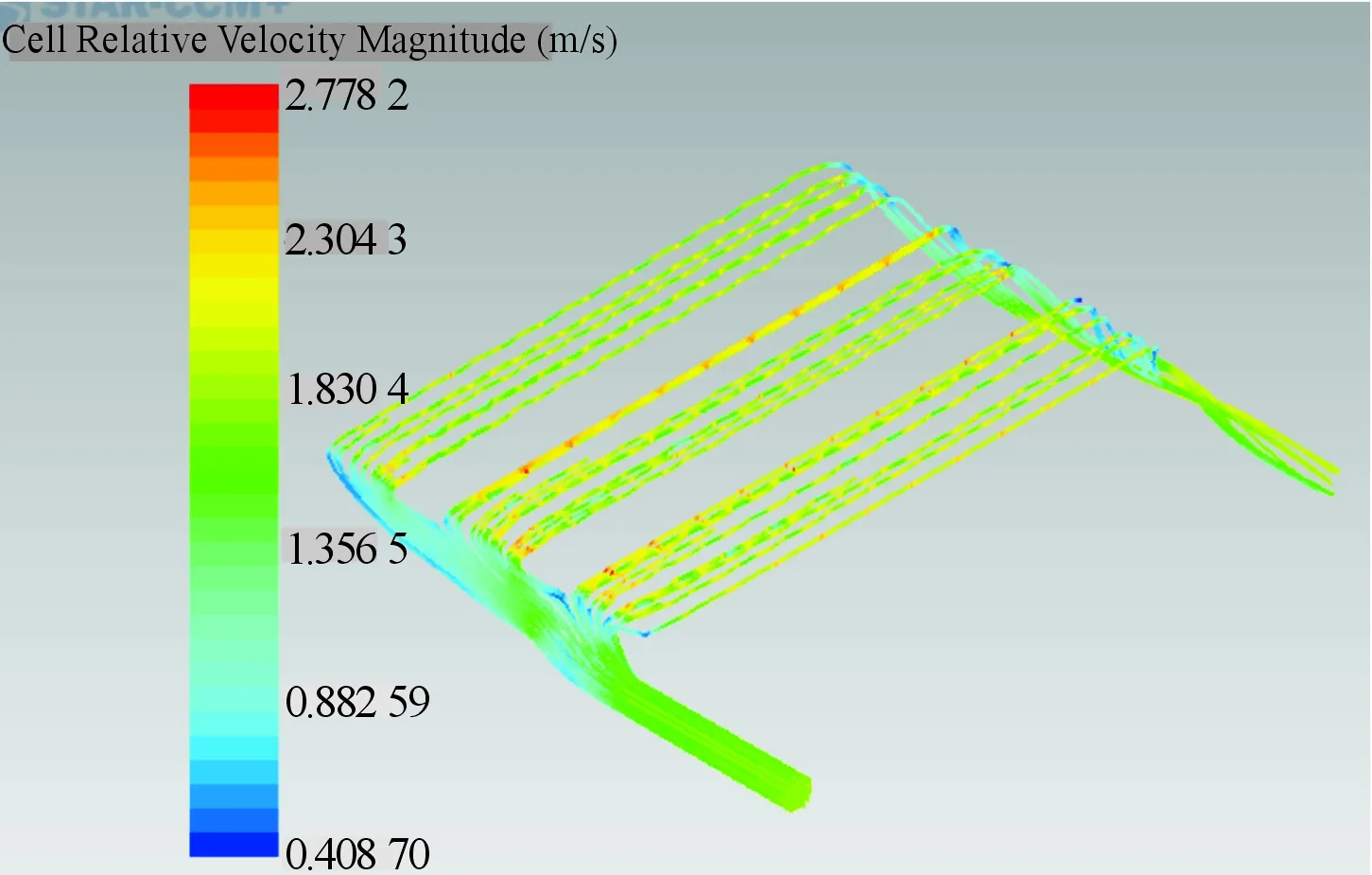
圖12 水道流線云圖

從以上分析結果可知：IGBT的溫度遠低于其可容許的最大溫限125 ℃，避免了熱害的發生并保證充分熱余量，水道的均勻性也較為理想，故此散熱結構能較好地滿足需求。

3.3 擾流塊不同高度參數下控制器整體數值模擬結果

本文選用的擾流塊最低高度是在滿足現有工藝基礎上制定的，水槽總高度為1 mm，擾流塊最小高度為0.6 mm，在模型、擾流塊、流量相同情況下，對不同高度的擾流塊分別進行模擬仿真。擾流塊模型高度如圖13所示，仿真結果如表3所示。

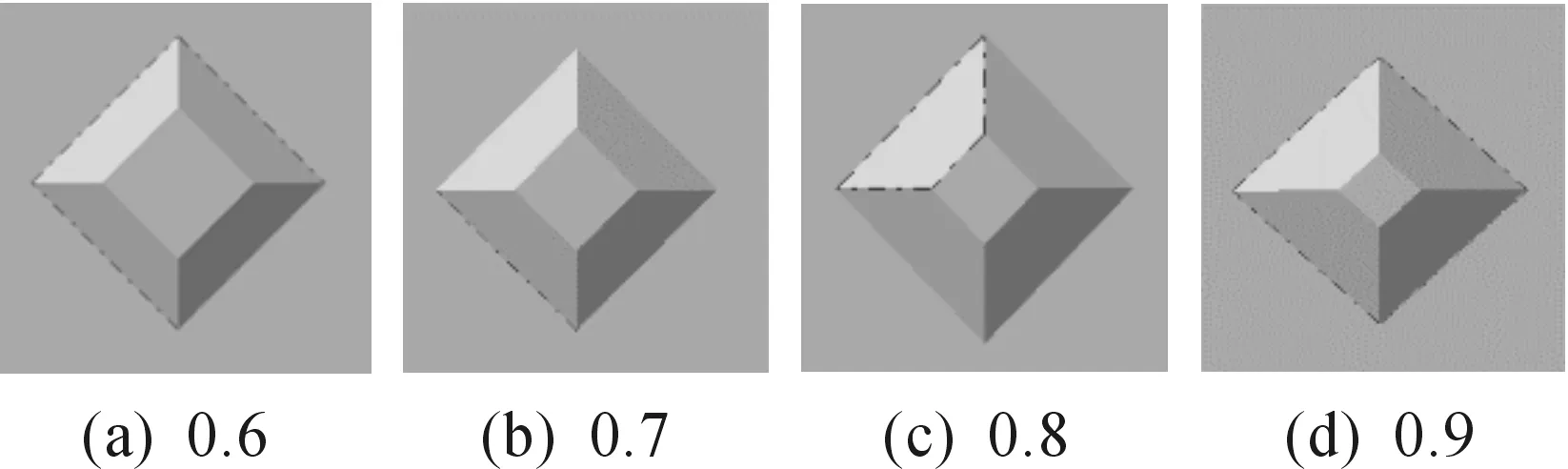
圖13 擾流塊模型高度(mm)

表3 不同高度擾流塊仿真結果

由表3數值模擬結果可知:隨著擾流塊高度增大，熱源IGBT的最大溫差為0.465 ℃，最大誤差為0.58%。擾流塊高度的增加使得可供冷卻液流過的橫截面積減小，但在相同流量下增強了冷卻液流動的速度，提高了散熱效率。隨著擾流塊高度的增加，控制器水道內的壓降也急劇變大，最大壓差為19 649.7 Pa，從滿足散熱性能和成本兩方面考慮，擾流塊的高度應選取0.7 mm最為合適。

3.4 不同擾流塊參數下控制器整體仿真結果

根據上述分析結果，選取0.7 mm作為擾流塊的高度，建立了如圖14所示的體積相同的擾流塊模型，保證了冷卻液所流過的橫截面相同。將3種擾流塊與無擾流塊水道進行對比，仿真結果如表4所示。

圖14 不同擾流塊模型

由表4可以分析得到:擾流塊的形狀對熱源溫度影響較小，最大溫差為0.23 ℃，相對IGBT來說溫差可忽略不計，但在未安裝擾流塊的水道中IGBT的溫度最高達到82.975 ℃，最大溫度誤差為3.79%，說明水道中安裝擾流塊有利于控制器的散熱。對比3種擾流塊可以發現：菱形的壓降最小，圓臺次之，正方形擾流塊的壓降最大。這是由于菱形比圓臺和正方形的迎水面都小，對水流的阻礙較小，使得壓力損失變小。對比速度數據得出正方形擾流塊的速度最大，其原因是迎水面的變大引起流體經過表面時發生分離得以加速。從速度跡線圖15可看出：加裝擾流塊和未加裝擾流塊的水道水流流動趨勢相同，但圓臺擾流塊在第3支道口處出現了斷流，會影響散熱效果，而未安裝擾流塊的水道水流速度較小且水道兩側的水流與中間相比流速更小，這樣會引起IGBT局部溫度過高。從圖16對比3種擾流塊對水流均勻性的影響發現：菱形擾流塊的均勻性相對較差，正方形擾流塊次之，圓臺最好，但是圓臺的斷流會影響散熱效果。總體分析來看：菱形擾流塊在滿足散熱性能和工藝要求下能達到工程要求。

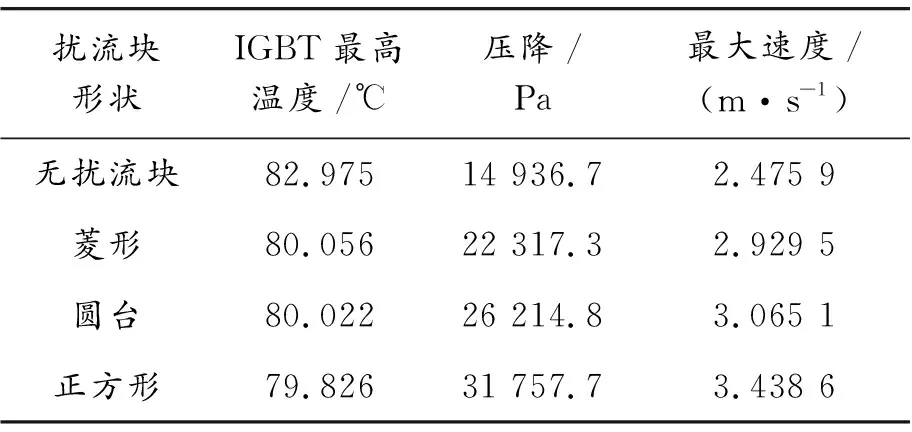
表4 不同擾流塊數值模擬結果

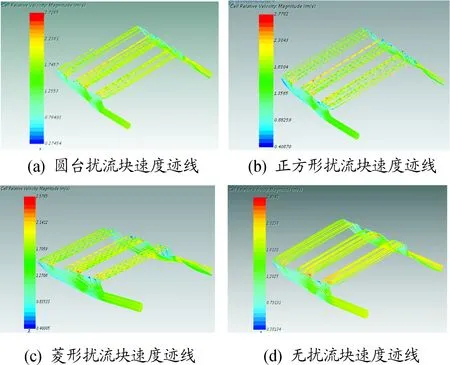
圖15 不同擾流塊速度跡線

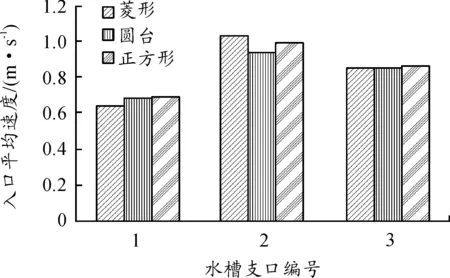
圖16 不同擾流塊平均流速

4 結論

1) 在保證網格質量相同的情況下，采用不同網格尺寸仿真結果變化較小，滿足網格無關性小于5%的要求。

2) 在滿足工藝要求的情況下，不同高度的擾流塊對IGBT溫度影響較小，但對速度和壓降影響較為明顯。

3) 擾流塊加裝與否對IGBT溫度影響較大，但不同形狀的擾流塊對IGBT溫度無明顯影響。