3x+1問題的證明

鮮 明， 周訓(xùn)偉，鮮 子

(1.遼寧省撫順市地理信息局， 遼寧 撫順 113008；2.北京聯(lián)合大學(xué) 北京市信息服務(wù)工程重點實驗室， 北京 100101；3.遼寧省撫順市圖書館， 遼寧 撫順 113006)

3x+1問題[1]是L.Collatz于1937年提出的一個數(shù)學(xué)猜想，也稱為Collatz問題、3x+1映射、Hasse’s 算法、角谷問題等。盡管有人[2]聲稱證明了3x+1問題，但一直不被人們所接受。M.R.Feix 和J.L.Rouet[3]，M.Chamberland[4]提出的方案也無效。文獻[5-13]只是階段性成果。E.Belaga[14]甚至懷疑3x+1問題的可證性。與此不同，本文將3x+1問題等價地變換成全奇項3x+1序列，由此導(dǎo)出等項方程式，將歸納法用于該等項方程式，最終證明3x+1問題為真。

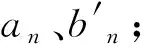
1 3x+1問題與全奇項3x+1序列

3x+1問題可用自然語言描述如下：從任意給定的正整數(shù)n出發(fā)，當它為偶數(shù)時就除以2，當它為奇數(shù)時就乘3加1；對每次所得結(jié)果重復(fù)上述運算，最終必能得到奇數(shù)1。例如：n=52，其運算結(jié)果為：26、13、40、20、10、5、16、8、4、2、 1。

稱上面的描述為3x+1問題的原始描述，為更清晰地描述并最終解決3x+1問題，引入“去偶”概念。設(shè)n=2ir，其中r∈No，i≥0，將n變?yōu)閞的過程稱為去偶過程或去偶運算，簡稱去偶。用“β()”表示去偶函數(shù)，即：β(n)=β(2ir)=(2ir)/2i=r。當n∈No時，β(n)=n。

根據(jù)上述定義可知：對于任一正整數(shù)n來說，必有β(n)∈No， 因此可以簡化3x+1問題。盡管3x+1問題所提出的被考察對象為任意正整數(shù)，但據(jù)3x+1問題的原始描述可以知道，假設(shè)從給定的“正整數(shù)n出發(fā)”，而當n=2ir(r∈No)時，需先進行i次除以2而得到r的工作，亦即首先要完成一個“去偶過程”。因此，可以把被考察對象n(n∈N)變?yōu)閞(r∈No)，而這種變化決不會對3x+1問題的本質(zhì)產(chǎn)生任何影響。

根據(jù)去偶概念，3x+1問題可簡述為：從任一正奇數(shù)r出發(fā)，反復(fù)進行乘3加1再去偶的運算，必在有限步驟內(nèi)得到奇數(shù)1。

不難理解，當把每一次乘3加1再去偶所得的結(jié)果順次記錄下來時，必然會得到一個每項均為奇數(shù)的序列(或數(shù)列)， 這種序列就是全奇項3x+1序列。

全奇項3x+1序列定義如下：

定義1 若序列E滿足如下關(guān)系：

e1∈No,e2=β(3e1+1),…,en+1=β(3en+1),…，

則稱E為全奇項3x+1序列。

例1 設(shè)全奇項3x+1序列E的第1項e1=11,于是有：

e2=β(3e1+1)=β(3×11+1)=β(2×17)=17;

e3=β(3e2+1)=β(3×17+1)=β(22×13)=13;

e4=β(3e3+1)=β(3×13+1)=β(23×5)=5;

e5=β(3e4+1)=β(3×5+1)=β(24×1)=1;

e6=β(3e5+1)=β(3×1+1)=β(22×1)=1;

……

即該全奇項3x+1序列E為：11，17，13，5，1，1，…。

請注意，e6，e7，以及其后的各項之值借助重復(fù)下述計算模式而得到：1乘3加1等于4,4被22除等于1。

不難看出，上述全奇項3x+1序列E從第5項開始，以后各項的值均等于1。

當把3x+1問題轉(zhuǎn)換為全奇項3x+1序列后就會發(fā)現(xiàn)，解決3x+1問題的關(guān)鍵在于證明下述的命題(稱之為證明目標)：所有的全奇項3x+1序列必然存在一個其值等于1的項。

為了敘述方便再給出如下定義：

定義2 若序列B中的項bi與項bj(i≠j)相等，則bi和bj均被稱為序列B中的相等項；若序列B有相等項，則B被稱為等項序列。

由此定義可知：如果項bi是序列B的相等項，那么，在B中必存在項bj(i≠j)使得bi=bj。

2 等項方程式

接著研究全奇項3x+1序列有相等項的充要條件。 考慮到可讀性問題，將把“必要條件”和“充分條件”作為2個定理分別給出。在此之前，先作如下定義：

定義3 設(shè)a0,a1,…,ak∈No.，再設(shè)a1=(3a0+1)/2i1,a2=(3a1+1) /2i2,…,ak=(3ak-1+1) /2ik，

那么稱i1,i2,…,ik為a0的k個連續(xù)成項指數(shù)，簡稱a0的k連指。

顯然，任意奇數(shù)a的k連指均為正整數(shù)。

例2 ① 求3的3連指；② 求1的k連指。

解

① 令a=3，那么a1=(3a+1)/2i1=(3×3+1)/21=5∈No，于是i1=1。同理i2=4，i3=2。

② 仿照①可求得1的k連指，即i1=i2=…=ik=2。

由例2可知：當一個奇數(shù)被給定時，它的k連指也一同被給定。

定理1 設(shè)全奇項3x+1序列E的第i項ei的k連指為i1,i2,…,ik，若ei=ei+k，則

ei=(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/(2i1+i2+…+ik-3k)

(1)

證明由k連指的定義可知:

ei+1=(3ei+1)/2i1

(2)

ei+2=(3ei+1+1)/2i2

(3)

……

ei+k=(3ei+k-1+1)/2ik

將式(2)代入式(3)得

ei+2=(32ei+3+2i1)/ 2i1+i2

同理：

ei+3=(33ei+32+3·2i1+2i1+i2)/ 2i1+i2+i3

……

ei+k=(3kei+3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/ 2i1+i2+…+ik

由ei=ei+k知：

ei=(3kei+3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/ 2i1+i2+…+ik

2i1+i2+…+ikei=3kei+3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1

2i1+i2+…+ikei-3kei=3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1

ei=(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1) /( 2i1+i2+…+ik-3k)

證明完畢。

定理2 若全奇項3x+1序列E有項ei滿足關(guān)系：

ei=(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/(2i1+i2+…+ik-3k)

其中i1,i2,…,ik為ei的k連指，則ei=ei+k。

證明由

ei=(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/(2i1+i2+…+ik-3k)

得：

(2i1+i2+…+ik-3k)ei=3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1

2i1+i2+…+ikei-3kei=3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1

2i1+i2+…+ikei=3kei+3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1

ei=(3kei+3k-1+3k-2·2i1+…+ 3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/ 2i1+i2+…+ik

(4)

另外，因序列E是全奇項3x+1序列，且i1,i2,…,ik為ei的k連指 (即i1,i2,…,ik分別為3ei+1,3ei+1+1,…,3ei+k-1+1中因子2的個數(shù))，所以又得到如下k個等式：

ei+1=(3ei+1)/2i1

ei+2=(3ei+1+1)/2i2

……

ei+k=(3ei+k-1+1)/2ik

仿定理1的推證過程得到：

ei+k=(3kei+3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)/ 2i1+i2+…+ik

(5)

由式(4) (5)得ei=ei+k。證明完畢。

接著用符號“x”來表示ei.于是式(1)變?yōu)槿缦碌男问剑?/p>

x=(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1) /( 2i1+i2+…+ik-3k)

(6)

由定理1和2可直接得到：

推論1 全奇項3x+1序列E有相等項x當且僅當x由式(6)給出。

該推論給出了任意全奇項3x+1序列有相等項的充要條件，其正確性不容置疑。但在表達上卻不太明確，為此再作如下闡述：由于式(6)是一個等式，可以把它看作以x及i1,i2,…,ik為變元的方程式(稱之為等項方程式)，并把x∈No,且i1,i2,…,ik為x的k連指這樣的解稱為特征解。

由定理1可知：當任意全奇項3x+1序列E有相等項x時，x必可表為式(6)，這意味著任意全奇項3x+1序列E有相等項，則等項方程式有特征解。同理，由定理2可得：等項方程式有特征解，則任意全奇項3x+1序列E有相等項。于是有如下推論：

推論2 任意全奇項3x+1序列有相等項的充要條件是式(6)有特征解。

推論1與推論2顯然是等價的，但推論2的表達更加明確。

不得不提的是等項方程式與圓周率π=c/d(c為圓的周長，d為直徑)之間有著驚人的相似之處。我們知道刻劃一個圓最重要的參數(shù)是圓的半徑r，可是π卻與r無關(guān)，這就使得本是一個圓的圓周率π便成了所有圓的圓周率。與此類似，刻劃序列的最重要參數(shù)是序列的項，而等項方程式卻與任意全奇項3x+1序列的項無關(guān)，因而也就使得等項方程式有無特征解這個本是某個全奇項3x+1序列有無相等項的判定條件卻成了所有全奇項3x+1序列有無相等項的判定條件。這一結(jié)果深刻地揭示出推論2的重要作用，并為3x+1問題的最終解決奠定了堅實的基礎(chǔ)。

3 最終證明

定理3 等項方程式

x=(3n-1+3n-2·2i1+…+3·2i1+i2+…+in-2+2i1+i2+…+in-1) /( 2i1+i2+…+in-3n)

(7)

僅有如下特征解：x=1，且i1=i2=…=in=2。

證明用數(shù)學(xué)歸納法證明。

第1步驗證n=1的情況。當n=1時，x=1 /( 2i1-3)。顯然，僅有i1=2使得x=1。由此可知，n=1時定理成立。

第2步假設(shè)n=k時，式(7)僅有如下特征解：

x=1，且i1=i2=…=ik=2

(8)

第3步證明當n=k+1時，

x=(3k+3k-1·2i1+…+3·2i1+i2+…+ik-1+2i1+i2+…+ik) /( 2i1+i2+…+ik+1-3k+1)

(9)

僅有如下特征解：x=1，且i1=i2=…=ik+1=2。

由歸納假設(shè)可知，僅有i1=i2=…=ik=2時可使得：

(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1) /( 2i1+i2+…+ik-3k)=1

3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1=2i1+i2+…+ik-3k

(10)

由式(9)可得

x=(3(3k-1+3k-2·2i1+…+3·2i1+i2+…+ik-2+2i1+i2+…+ik-1)+2i1+i2+…+ik) /( 2i1+i2+…+ik+1-3k+1)

(11)

將式(10)代入式(11)得：

x=(3( 2i1+i2+…+ik-3k)+2i1+i2+…+ik) /( 2i1+i2+…+ik+1-3k+1)

x=(4·2i1+i2+…+ik-3k+1) /( 2i1+i2+…+ik+1-3k+1)

( 2i1+i2+…+ik+1-3k+1)x=(4·2i1+i2+…+ik-3k+1)

2i1+i2+…+ik(2ik+1x-4)=3k+1(x-1)

(12)

由式(12)可知：當i1,i2,…,ik∈N時必有：( 2ik+1x-4)=0且(x-1)=0；ik+1=2且x=1。

從以上推證過程可知，僅當i1=i2=…=ik=2且ik+1=2時，x=1。

這樣就證明了式(9)僅有如下特征解：

x=1，且i1=i2=…=ik+1=2

(13)

證明完畢。

定理4 3x+1問題為真。

給出如下兩種證法：

證法1 由定理1的證明可知，只要假設(shè)全奇項3x+1序列E有相等項x，且x的k連指為i1,i2,…,ik，就能得到等項方程式。由推論1與定理3可知序列E有相等項1。由序列E的泛指性可知任意全奇項3x+1序列必有相等項1。所以，證明目標為真。故該定理成立。

證法2 定理3告訴我們，式(6)必有式(8)給出的特征解。由推論2知任意全奇項3x+1序列必有相等項。定理3還告訴我們，所有的相等項均等于1。所以，任意全奇項3x+1序列中有其值等于1的項。于是證明目標為真。故該定理成立。

證明完畢。

注釋1對幾個質(zhì)疑的簡單解答

本文完成后曾受到學(xué)界一些學(xué)者和朋友的質(zhì)疑，盡管這些質(zhì)疑最終并不正確，但是在這些質(zhì)疑的背后卻隱藏著諸多深層次問題。下面是對這些質(zhì)疑的討論。

1 對數(shù)學(xué)歸納法的理解

質(zhì)疑1 在定理3的證明中對數(shù)學(xué)歸納法的應(yīng)用不正確。

該質(zhì)疑有3種觀點：一是認為應(yīng)該對式(8)是式(6)的唯一特征解給出證明；二是認為將式(10)代入式(11)是不能被允許的；三是認為由定理3給出的問題不能用數(shù)學(xué)歸納法來證明。

以上質(zhì)疑，問題出在質(zhì)疑者對數(shù)學(xué)歸納法的理解不正確。為了對癥下藥，筆者只好在此重述數(shù)學(xué)歸納法的基本原理和思想。

數(shù)學(xué)歸納法說到底是邏輯學(xué)中假言推理肯定式一個最經(jīng)典的應(yīng)用，所以要理解數(shù)學(xué)歸納法必須知道假言推理肯定式這一基本邏輯規(guī)則。假言推理肯定式可表述為：若A則B為真，且A為真，則B為真。這里的“為真”相當于我們常說的“成立”，“ 若A則B”相當于“A是B的充分條件”。除此之外，還應(yīng)該知道數(shù)學(xué)歸納法的第2步和第3步在干什么。數(shù)學(xué)歸納法的第2步：假設(shè)p(k)為真。第3步：推出p(k+1)為真。顯然，這2步加在一起是在完成若p(k)則p(k+1)為真的證明。

另外，由于任意具有真理性的結(jié)論被推出，其所有前提只能是定理或事實，所以在這一過程中既沒有確定p(k)為真(因為p(k)為真是被假設(shè)的)，也沒有確定p(k+1)為真(因為p(k+1)為真是在假設(shè)p(k)為真的基礎(chǔ)上得到的，不能被視為具有真理性的結(jié)論)，那么，p(n)為真是怎樣得到的呢？

推出p(n)為真的過程是：因為已經(jīng)證明了若p(k)為真則p(k+1)為真，那么，當k=1時便有：若p(1)為真則p(2)為真，由于已驗證p(1)為真，根據(jù)假言推理肯定式得p(2)為真。同理，當k=2時，可得p(3)為真，…，以此類推，當k=n-1時，可得p(n)為真。

當我們對數(shù)學(xué)歸納法的推理過程有清晰的認識后就會發(fā)現(xiàn)：① 式(8)是式(6)的唯一特征解是歸納假設(shè)，而假設(shè)是不需要證明的；② 式(10)是由歸納假設(shè)推出的結(jié)果，將式(10)代入式(11)是一種合理的等價替換，不存在不可代入的問題；③ 由于數(shù)學(xué)歸納法本質(zhì)上是假言推理，而假言推理對象并不存在特殊要求，所以定理3完全可用數(shù)學(xué)歸納法來證明。

2 對列方程解應(yīng)用題的討論

質(zhì)疑2 由定理2不能得出“若等項方程式有特征解則全奇項3x+1序列E有相等項” 這一結(jié)果。

為了讓得出過程更加清晰，我們采用了在不依據(jù)定理2的情況下得到以上結(jié)果的方法來完成對質(zhì)疑的回答。

考察中學(xué)數(shù)學(xué)課本中列方程解應(yīng)用題的相關(guān)內(nèi)容。中學(xué)課本中的應(yīng)用題有一個共同特點：針對所給問題總可以列出一個或多個方程來與問題相對應(yīng)。因而這類問題又被稱為可列方程問題。

當針對應(yīng)用題(或可列方程問題)列出與之對應(yīng)的方程后，在我們面前就產(chǎn)生了2個對象：一個是所給的應(yīng)用題(稱原問題)，另一個是列出的方程(稱所列方程)。于是，出現(xiàn)了2個需要問的事情：① 求原問題的解為什么可以通過求所列方程的解來實現(xiàn)？② 所列方程的什么解或哪些解才是原問題的解？為了回答這些問題先來看一個例子。

問題1 已知一整數(shù)的平方與一正整數(shù)之和等于3，求這2個數(shù)。

解設(shè)所求的整數(shù)為x，所求的正整數(shù)為y，由題意得

x2+y=3

(14)

在這里，問題1是原問題，方程式(14)是所列方程。表面上看這兩者差別很大，沒有共同之處，然而它們卻有著完全相等的成分。因為x被設(shè)定為一整數(shù)，所以x2便可以讀作“一整數(shù)的平方”。同理，y可以讀作“一正整數(shù)”，于是方程式(14)可以讀作“一整數(shù)的平方與一正整數(shù)之和等于3”。由此我們看到了問題1與式(14)之間的相互重合的現(xiàn)象。這一重合現(xiàn)象告訴我們，求原問題的解完全可以通過求所列方程的解來實現(xiàn)。

另外，單從方程的角度看，式(14)的x和y可以為任意實數(shù)或復(fù)數(shù)。但是，要使得式(14)與問題1之間具有重復(fù)性(即同一性)，其中的x必須為整數(shù)，y必須為正整數(shù)。這里的x、y被稱為變元，對變元x或y的設(shè)定條件稱為約束條件。這樣，更準確地說只有在所有變元滿足約束條件的情況下，所列方程與原問題之間才具有同一性。既然在這種情況下這兩者同一，那么，這兩者的解必然相同。剩下的問題只需要我們弄清在這種情況下所列方程的解是一些什么樣的解就可以了。

所謂方程的解，從形式上看就是對相關(guān)變元的一次取值。對于所列方程而言，若每個變元的取值均滿足其對應(yīng)變元的約束條件，那么這樣的解(稱有效解)就是該所列方程的變元在滿足約束條件的情況下的解。由此可知，所列方程的所有有效解均是原問題的解。

通過求解方程(14)可得該方程的3個有效解：

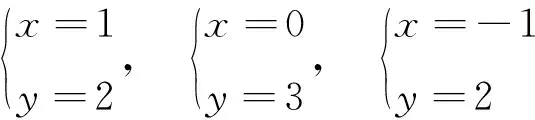
不難驗證這些有效解都是問題1的解。顯然如下結(jié)論成立：

結(jié)論1 原問題有解當且僅當所列方程有有效解。

根據(jù)以上討論來再次證明若等項方程式有特征解則全奇項3x+1序列E有相等項。

證明由定理1的證明可知，只要假設(shè)全奇項3x+1序列E有相等項x，且x的k連指為i1,i2,…,ik，就能得到等項方程式。這一事實告訴我們，求全奇項3x+1序列E的相等項這個問題是可列方程問題(即應(yīng)用題)。這時，求全奇項3x+1序列E的相等項是原問題，等項方程式是所列方程。由結(jié)論1知，若等項方程式有有效解則全奇項3x+1序列E有相等項。由于等項方程式的特征解就是它的有效解，于是所證結(jié)論成立。

以上證明(事實上給出了推論2的第2種證法)讓我們更加清楚地看到等項方程式的特征解與全奇項3x+1序列E有相等項之間的直接聯(lián)系，從而可以消除對“等項方程式有特征解則全奇項3x+1序列E有相等項”的正確性的懷疑。其實，結(jié)論1的成立本身就意味著推論2的成立。

然而，在此又有人提出質(zhì)疑，他們認為“假設(shè)全奇項3x+1序列E有相等項x”預(yù)設(shè)了“全奇項3x+1序列有相等項”這一前提，因而是不被允許的。對此作如下簡單解釋：

此質(zhì)疑不能成立的直接理由是： 如果“假設(shè)全奇項3x+1序列E有相等項x”真的預(yù)設(shè)了“全奇項3x+1序列有相等項”，那么，按照質(zhì)疑者的說法，那就必須在確認了“全奇項3x+1序列E有相等項”之后才能“假設(shè)全奇項3x+1序列E有相等項x”，亦即必須在確認了“全奇項3x+1序列E有相等項”之后才能“假設(shè)全奇項3x+1序列E有相等項”。這顯然是不合理的，這種說法直接否認了假言推理的合法性。

從數(shù)學(xué)歸納法的討論中看到：要實現(xiàn)對“若A則B為真”的確立，可采取假設(shè)A為真推出B為真的方法來完成。一般來講，這被假設(shè)對象A應(yīng)該滿足如下要求：若A不必然為假(或真)，則可以假設(shè)A為真(或假)。如果A必然為真再假設(shè)A為假，或者如果A必然為假再假設(shè)A為真都是沒有意義或錯誤的。因為，A必然為假(或真)等價于：“事實”上A為假(或真)，如果此時再“假設(shè)”A為真(或假)，這時的“事實”與“假設(shè)”必然矛盾。而前提中存在矛盾的任何推理其結(jié)果都是沒有意義的。

根據(jù)以上討論可知“假設(shè)任意全奇項3x+1序列E有相等項x”是合理的。因為至目前為止在所能驗證的全奇項3x+1序列中均有相等項，即“任意全奇項3x+1序列E有相等項”不必然為假，所以可以假設(shè)它為真。然而，如果某一天有人發(fā)現(xiàn)某全奇項3x+1序列無相等項，那么在那時就不能再“假設(shè)任意全奇項3x+1序列E有相等項x”為真了，因為那時“任意全奇項3x+1序列E有相等項”必然為假。一句話，在發(fā)現(xiàn)某全奇項3x+1序列無相等項之前上述假設(shè)是合理的、有意義的或被允許的；在發(fā)現(xiàn)某全奇項3x+1序列無相等項之后上述假設(shè)是不合理的、無意義的或不被允許的。同時，這一結(jié)果背后還蘊含著一個深刻的道理：事實與定理﹑公理等在推理過程中具有同等重要的地位和作用。

還有一些不具討論價值的質(zhì)疑就不在此一一解答了。

注釋2K連指的特征與序列的循環(huán)性

本注釋給出了幾個具有參考價值的結(jié)果，有興趣的讀者可以一讀。

為了方便討論，把定義3中的a0稱為ak的k級前項，ak稱為a0的k級后項。當k=1時，稱a0為ak的直接前項，ak為a0的直接后項。

由定義3可知，ak-1=(2ikak-1) /3，稱此式為前項關(guān)系式。

定義4 設(shè)前項關(guān)系式中的ak∈No。若有ik使得ak-1∈No，則稱ak為序中項，否則稱ak為序始項。

引理1 ① 若奇數(shù)a≡0(mod 3),則a為序始項。② 若奇數(shù)a≡1(mod 3),則a為序中項。當i分別為2,4,…,2n時，a有n個不同的直接前項，這n個不同的直接前項的1連指分別為2,4,…,2n。③ 若奇數(shù)a≡2(mod 3),則a為序中項。當i分別為1,3,…,2n-1時，a有n個不同的直接前項，這n個不同的直接前項的1連指分別為1,3,…,2n-1。

證明只證③。設(shè)b=(2ia-1) /3。 因為a≡2(mod 3),令a=3k+2。當i=2n-1時，

2ia-1=22n-1(3k+2) -1=22n-13k+22n-1

由于22n≡4n≡1(mod 3),所以，2ia-1=22n-13k+22n-1 ≡0(mod 3)，且b=(2ia-1) /3∈No。

由此可知b是a的前項。于是a為序中項。同時，(2a-1) /3，(23a-1) /3,…,(22n-1a-1) /3這n個不同的直接前項的1連指分別為1,3,…,2n-1。證明完畢。

由引理1可知任意一個序中項必有無窮多個(k級)前項。

定義5 如果兩個長度相同的序列A：a1,a2,…,an和B：b1,b2,…,bn滿足條件a1=b1,a2=b2,…,an=bn則稱A和B為相同序列，用A=B表示，否稱A和B為不相同序列，用A≠B表示。

引理2 設(shè)序列A：a1,a2,…,an和B：b1,b2,…,bn，A≠B。u1,u2,…,ur為互不相同的r個數(shù)，v1,v2,…,vs為互不相同的s個數(shù)。那么，如下的r+s個長度為n+1的序列為互不相同的序列：

T1：u1,a1,a2,…,an

T2：u2,a1,a2,…,an

…

Tr：ur,a1,a2,…,an

Tr+1：v1,b1,b2,…,bn

Tr+2：v2,b1,b2,…,bn

…

Tr+s：vs,b1,b2,…,bn

證明當1≤i≤r，r

結(jié)論2 設(shè)a為序中項，那么a的任意兩個不同的k級前項的k連指是不同的。

證明為了提高可讀性，以7為例來證明此結(jié)論。

由引理1可知，7的直接前項為：9,37,149，…，(7·22n-1)/3，….，它們對應(yīng)的1連指分別為：2,4,6，…，2n，….。7的直接前項中每個序中項如：37,149….又有直接前項。37的直接前項有：49,197,789，…，(37·22n-1)/3，…。對應(yīng)的1連指為：2,4,6，…，2n，…。149的直接前項有：99,397,1 589，…，(149·22n-1)/3，…。對應(yīng)的1連指為：1,3,5，…，2n-1，…。如此等等。

為了讓問題清晰化，把每個序中項的直接前項用線段連接起來就得到如圖1所示的1顆無窮樹，稱這棵樹為7的k級前項樹。為了方便，把根節(jié)點7稱為樹的第0層，它的上一層為第1層，…，以此類推。第1層包含了7的所有直接前項，第2層包含了7的所有2級前項，…，第k層包含了7的所有k級前項。樹中帶括號的節(jié)點為序始項。

另外，樹中的每個節(jié)點均為奇數(shù)，而每個奇數(shù)必有唯一1連指與之對應(yīng)。把圖1中的奇數(shù)換成它對應(yīng)的1連指就得到圖2。圖2被稱為7的k連指樹。

由圖1可得到7的k級前項的全奇項3x+1序列。例如，7的3級前項1 045，與它直接相連的下層節(jié)點為49，與49直接相連的下層節(jié)點為37，與37直接相連的下層節(jié)點為7。于是得到全奇項3x+1序列的前4項：1 045,49,37,7。

與此同時，利用圖2可得到1 045的3連指。其方法如下。先找到1 045在圖1中的位置，為第3層的第3位，再找圖2中相應(yīng)位置上的數(shù)，該數(shù)為6。 與6直接相連的下層節(jié)點為2，與2直接相連的下層節(jié)點為4。于是得到1 045的3連指：6,2,4。

下面來指明7的k級前項的k連指是互不相同的。圖2中第1層的每個數(shù)是互不相同的，所以7的1級前項的1連指是互不相同的。根據(jù)圖2和引理2可知7的所有2級前項的2連指互不相同。同理，當7的k級前項的k連指互不相同時，由引理2可證，7的k+1級前項的k+1連指互不相同。

顯然，按照生成圖1的方法可以得到任意奇數(shù)a的k級前項樹。接著，按照生成圖2的方法可以得到a的k連指樹。不難看出，a的k連指樹與7的k連指樹具有相同的性質(zhì)，所以任意奇數(shù)a的k級前項的k連指是互不相同的。證明完畢。

圖1 7的k級前項樹

圖2 7的k級連指樹

定義6 若全奇項3x+1序列A的第1項為序始項，則稱A為完整序列，否則稱A為不完整序列。

定義7 若序列B是序列A去掉前k項后形成的序列，則稱B是序列A的子序列。

在結(jié)論2的證明中知道7的直接前項有：9,37,149，等等。不難看出：37=4×9+1，149=4×37+1，9 ≡0(mod 3)，37 ≡1(mod 3)，149 ≡2(mod 3)。

事實1 任意一個序中項a的直接前項中至少有一個序中項。

引理3 若奇數(shù)a≡r(mod 3),則4a+1 ≡r+1(mod 3)。(證明從略)

引理4 設(shè)a1=(2ia-1)/3∈N。那么，若a2= 4a1+1則a2=(2i+2a-1)/3∈N。

證明a2=4a1+1=4(2ia-1)/3+1=(4·2ia-4 +3)/3=(2i+2a-1)/3∈N。證明完畢。

引理4清楚地指明了a的兩個相鄰的直接前項a1和a2的相互關(guān)系。

結(jié)論3 任意不完整序列必為完整序列的子序列。

證明設(shè)A：a1,a2,…,an…為不完整序列。由定義6知a1為序中項，設(shè)a1的直接前項為v1，于是必有全奇項3x+1序列B：v1,a1,a2,…,an…，且A是B的子序列。

若v1≡0(mod 3)，則B是完整序列，結(jié)論成立。

若v1≡2(mod 3)，令v2=4v1+1。由引理3知v2≡0(mod 3)。 由引理4與v1是a1的直接前項知，v2是a1的直接前項。這時有完整序列B：v2,a1,a2,…,an…。于是結(jié)論成立。

若v1≡1(mod 3)，令v3=4(4v1+1)+1。由引理3知，v3≡0(mod 3)，于是B：v3,a1,a2,…,an…是完整序列。結(jié)論成立。

證明完畢。

大家知道，序列A：a1,…,ai -1,ai,…,ai+ k-1,ai,…,ai+ k-1,…被稱為(循環(huán)長度為k的)循環(huán)序列。循環(huán)序列有如下重要性質(zhì)：

性質(zhì)1 設(shè)B是A的子序列。那么：① 若A是循環(huán)序列則B是循環(huán)序列；② 若B是循環(huán)序列則A是循環(huán)序列。

對于全奇項3x+1序列A而言，如果A有相等項則A是循環(huán)序列，反之亦然。

下面命名兩種序列。若A的第1項為a則稱A為首a序列。若A的第1項是a的(k級)前項，則稱A為a的(k級)前項序列。于是有：

事實2 首a序列必為a的前項序列的子序列。

例如：全奇項3x+1序列A：9,7,11,17,…和B：7,11,17,…。A,B分別為首9序列和首7序列，且A分別是7,11,17,…的前項序列。由于A是7的前項序列，所以首7序列B是A的子序列。

結(jié)論4 設(shè)A是a的一個前項序列，那么若A為循環(huán)序列則a的所有前項序列為循環(huán)序列。

證明由題設(shè)與事實2可知，首a序列為A的子序列。由A為循環(huán)序列和性質(zhì)1的①知，首a序列為循環(huán)序列。由于a的任意前項序列均以首a序列為子序列，所以由性質(zhì)1的②知，a的任意前項序列為循環(huán)序列。證明完畢。

由于全奇項3x+1序是無窮序列，所以它的每一項均有后項，后項還有后項，以致于使得序列向右端無限延伸。與此同時，對于a的某前項序列而言，當a的前項為序中項時，由事實1知，a的前項還有前項，前項還有前項，以致于使得序列向左端無限延伸。即有如下事實：

事實3 在a的前項序列中至少存在一個向左右兩端無限延伸的序列A。

我們知道任意兩個無窮小的極限相等且為0，這已成為人們的共識，因此有如下公理：

公理1 同屬于一個集合的兩個無窮大的極限相等。

結(jié)論5 任意全奇項3x+1序列為循環(huán)序列。

證明只證任意序中項a的任意前項序列為循環(huán)序列。

根據(jù)事實3可設(shè)A是a的前項序列中向左右兩端無限延伸的序列。

先證A必為循環(huán)序列。在A中有無窮多個a的前項和無窮多個a的后項。若在a的前項中存在相等項或在a的后項中存在相等項，那么A為循環(huán)序列。若在a的前項中不存在相等項且在a的后項中也不存在相等項，那么A的左右兩端必然為無窮大，且這兩個無窮大均為序中項。由公理1知A中有相等項，即A為循環(huán)序列。

由結(jié)論4與A為循環(huán)序列知，a的所有前項序列為循環(huán)序列。

證明完畢。

顯然，由結(jié)論5和定理3可得3x+1問題的又一新的證法，所以本注釋頗具參考價值。

致謝

感謝崔同慶教授對研究的鼓勵與關(guān)心。