利用二部圖生成概念格

竇林立，展正然

形式概念分析又稱概念格[1-2]，是由德國Wille教授在20世紀80年代首次提出的，它提供了一種支持數據分析和知識處理的數學工具[3-4]。近些年來，國內外各位學者提出了許多的構造算法。例如：Godin等[5]提出了概念格的漸進生成算法；Ho[6]提出了基于概念格的概念聚類算法；張文修等[7]給出了在保持格同構的條件下建立概念格的屬性約簡的方法；Elloumi等[8]基于模糊形式背景建立了一個多層次的約簡理論。

近幾年許多學者從圖論方面對概念格進行研究。例如：Amilhastre 等[9]與 Berry 等[10-12]將二部圖與概念格進行了交叉研究；李立峰等[13-14]利用弦二部圖和鏈圖對概念格進行表示；張濤等[15-17]利用屬性樹和屬性拓撲圖來表示形式背景，簡化了形式背景的表示結構，并提出了基于樹圖的屬性約簡算法。本文通過二部圖的極大完全子圖的概念來生成概念格，給出了基于二部圖的深度優先的概念格的迭代算法。

1 基本概念

本節主要介紹概念格與二部圖的基本知識。關于概念格的更多內容參見文獻[1,18]，有關圖論的詳細內容參見文獻[19-20]。

1.1 概念格

定義1 1)在形式概念分析中，一個形式背景是一個三元數組，其中O是對象集合，M是屬性集合，I是O與M之間的一個二元關系。用表示“對象有屬性” 。對于及， 定 義 ：，。則形式背景的概念定義為元素對，其中，，，。概念的外延是A，內涵是B。

通過上述兩種方法約簡形式背景后，就可以有效地減少形式背景中屬性集合中的元素個數，從而降低生成概念格的難度，更迅速地生成概念格。

表1 形式背景(O,M,I)Table 1 Formal context (O,M,I)

表2 約簡后的形式背景(O,M,I)Table 2 Reduced formal context (O,M,I)

1.2 圖論

由概念格和二部圖的定義可知，每個形式背景都對應一個二部圖，其中二部圖的頂點集為，頂點與之間有一條邊當且僅當與滿足關系I。

下面用具體實例來說明以上定義。

例2 圖1是例1中約簡后的形式背景表2對應的二部圖，圖2是表2對應的概念格，原形式背景表1對應的概念格即為圖3。

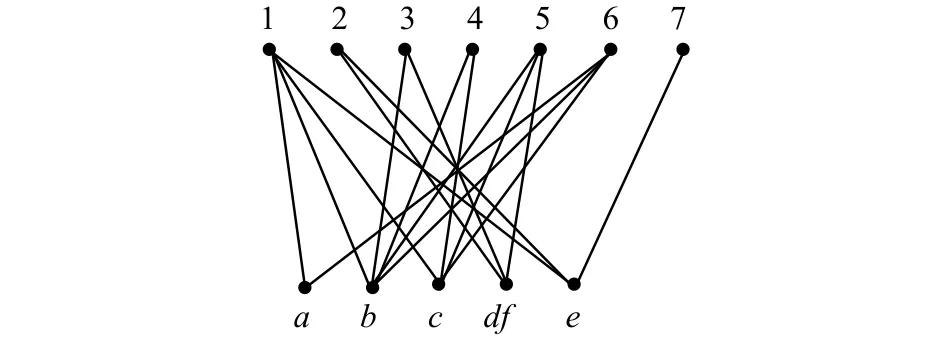
圖1 表2對應的二部圖Fig. 1 Bipartite graph for table 2

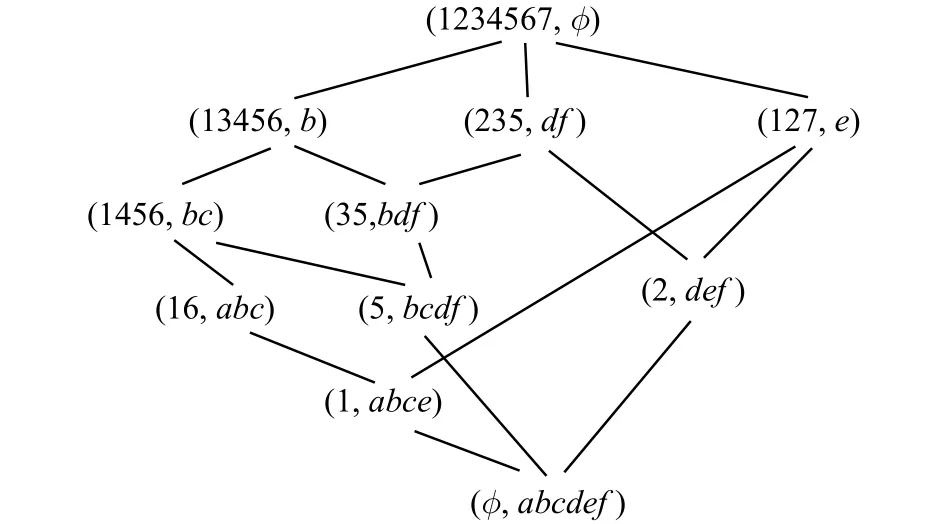
圖2 表2對應的概念格Fig. 2 Concept lattice for table 2

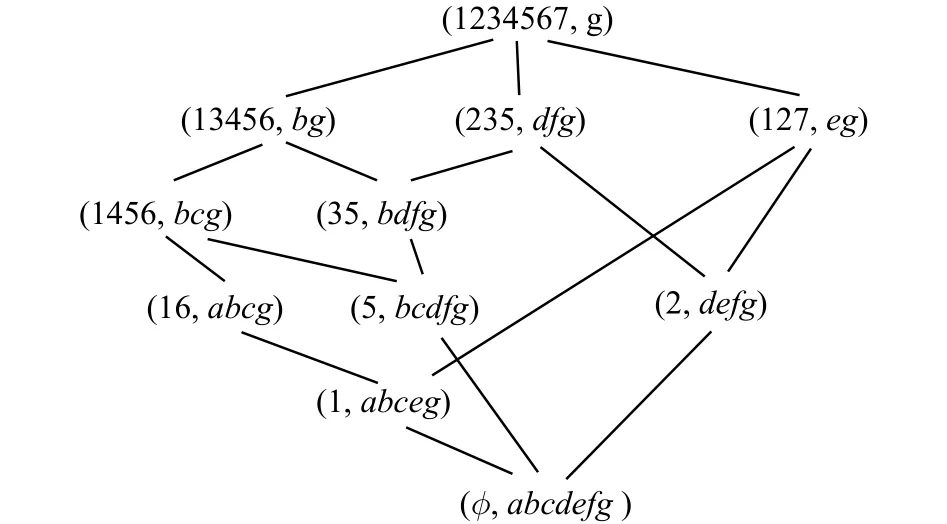
圖3 表1對應的概念格Fig. 3 Concept lattice for table 1

2 利用二部圖生成概念格

形式背景中的數據，在很多情況下，對象的個數較大，而屬性的個數則相對較少，在這種情況下，基于屬性來生成概念格，可以有效地減少算法的執行時間。本文基于屬性，利用二部圖子圖和鄰集的知識來生成概念格。

本節中的形式背景是指約簡后的形式背景，二部圖也指約簡后的形式背景所對應的二部圖。

首先給出二部圖的極大完全子圖的定義。

定義4 若 S 是二部圖 G 的子圖，且 S是完全二部圖，對任意的 v ∈V(G)?V(S)， G 由 V (S)∪v導出的子圖 G [V(S)∪v]不是完全二部圖，則 S稱為二部圖G的極大完全子圖。

下面給出二部圖的極大完全子圖與概念的對應關系。

證明 由概念格的定義知充分性顯然成立。

下面的定理2和定理3就是利用二部圖的極大完全子圖得到頂層概念 (O ,?)的直接子概念。

定理2 形式背景 K =(O,M,I)對應的二部圖為G=(O,M;E)，i 為圖 G 的頂點集 M 中度數最大的頂 點 ， N(i)=P ，則i 與 P 構 成 的 G 的 導 出 子 圖G[P∪i]是 G 的極大完全子圖，即 (P ,i)為概念，且(P,i)為頂層概念( O ,?)的直接子概念。

證明 用反證法。假設 G [P∪i]不是 G的極大完全子圖，即存在 o ∈O?P ，有 S1=(P∪o,i;E1)為完全二部圖，或存在 m ∈M，有 S2=(P,i∪m;E2)為完全二部圖。若有第一種情況，則頂點 i 與 P ∪o相鄰，此與 N (i)=P矛盾。若有第二種情況，由完全二部圖的定義知 i ∪m與P中每個頂點都相鄰，如果m的鄰集恰好為P，則i與m應約簡為im，與i和m是兩個頂點矛盾；如果m的鄰集包含P，即至少存在 o1∈O ，使 m 與 P ∪o1相鄰，則 m 的度數大于i的度數，此與i為 M 中 度數最大的頂點矛盾。因此，G[P∪i]是G的極大完全子圖，即 (P ,i)為概念。且其為頂層概念 (O ,?)的直接子概念，因為不存在概念 C ，使(P,i)＜C ＜ (O,?)。

定理3 若 j 是形式背景 K =(O,M,I)對應的二部圖 G =(O,M;E)的頂點集 M 中除i外度數最大的頂點， N (j)=P?。若 P?? P ，則 (P?,j)為頂層概念(O,?)的直接子概念；若 P?? P ，則以 P?為外延的概念應為 (P ,i)的子概念。

證明同定理2。

證明 (P ,i)為形式背景 K 的概念， ( Q,j)為形式背景 K?的概念，前文已證。下證 (Q ,i∪j)為形式背景 K 的概念，即需證 G Q,i∪j 為二部圖 G 的極大完全子圖。

用反證法。假設 G Q,i∪j 不是二部圖 G 的極大完全子圖，那么可能有下列兩種情況：1）至少存在 o ∈P?Q,使 G Q∪o,i∪ j為完全二部圖；2）至少存在 m ∈M?i?j ，使 G Q,i∪ j∪m為完全二部圖。如果出現第一種情況，由完全二部圖的定義知在圖 S 中頂點 j 與 Q ∪o中的每個頂點相鄰，此與在形式背景 K?中 N (j)=Q矛盾。如果出現第二種情況，由完全二部圖定義知在圖S中m與集Q中的每個頂點相鄰，那么m在S中的鄰集必包含j在S中的鄰集，這與形式背景已約簡且j是S的頂點集中 度數最大的頂點相矛盾。所以為形式背景K的概念，并且不能找到集合B，使，因此 (Q ,i∪j)是( P ,i)的直接子概念。

根據定理4可以通過求 G 的導出子圖的概念來簡化形式背景，并求出 (P ,i)的直接子概念。這樣經過反復的分解和約簡，使形式背景越來越簡化，同時也能求出的所有子概念。

因此便能生成頂層概念的所有直接子概念以及它們各自的子概念。這便是基于二部圖的深度優先的概念格的迭代算法。

基于二部圖的深度優先的概念格的迭代算法：

1) 最頂層概念為 (O ,?)，標號為1。

2) 形式背景 K =(O,M,I)(約簡后)，其對應的二部圖為 G =(O,M;E)，取屬性M中度數最大的頂點i ， N (i)=P ，則 (P ,i)為頂層概念 (O ,?)的直接子概念，標號為21。

3) 畫出 G 的導出子圖 S1=G[P∪(N(P)?i)](約簡后)，其對應的形式背景為 K1。取二部圖 S1的屬性集 N (P)?i 中度數最大的頂點 i1， N (i1)= P1，則(P1,i1)為形式背景 K1的概念， ( P1,i∪i1)為形式背景K 中概念 (P ,i)的直接子概念，標號為31。

4) 畫出 S1的導出子圖S2=S1[P1∪(N(P1)?i1)](約簡后)，其對應的形式背景為 K2，取二部圖 S2的屬性集 N (P1)?i1中度數最大的頂點 i2， N (i2)=P2，則 (P2,i2)為形式背景 K2的概念，故 (P2,i∪i1∪i2)為形式背景K中概念 (P1,i∪i1)的直接子概念，標號為41。繼續下去，直到 Pl為 單點集，則(Pl,i∪i1∪i2···∪il)為形式背景K的倒數第二層概念，它由導出子圖Sl生成，其直接子概念為最底層概念 (? ,M)，標號為 (l +2)1，最底層概念 (? ,M)的標號為 l+ 3。

5) 從標號為 r1 的概念回到生成它的導出子圖Sr?2，考察二部圖 Sr?2的屬性集中未考慮過的度數最大的頂點 ir?2?。如果 N (ir?2?)=Pr?2?是已生成的概念的外延，且當此已生成概念的內涵包含i∪i1∪i2···∪ir?2?時，說明以 Pr?2?為外延的概念及其子概念已生成，則不必再考慮此頂點；而當此已生成概念的內涵等于時，則是的直接子概念，且此概念及其子概念已生成(已標號)，此頂點也不必再往下考慮。如果 Pr?2?不 是 已 生 成 概 念 的 外 延 ， 則 (Pr?2?,ir?2?)是(Pr?1,ir?1)的直接子概念，標號為 (r ?1)2，然后按步驟3）和步驟4）的方法畫出 Sr?2的導出子圖Sr?1?=Sr?2[Pr?1?∪ (N(Pr?1?)? ir?1?)]，接著再取未考慮過的最大度數頂點生成概念，直到倒數第二層概念。

3 實例

下面通過例3來具體說明此方法如何產生概念格。

例3 形式背景同例1，其中的對象O={1,2,3,4,5,6,7}表示1班至7班共7個班級，屬性M={a,b,c,d,e,f,g}表示班級特色，其中a表示團結，b表示紀律嚴明，c表示學風端正，d表示衛生環境好，e表示干部隊伍過硬，f表示英語四六級通過率高，g表示課余活動豐富。

下面用基于二部圖的深度優先的概念格的迭代算法來生成概念格。

1) 最頂層概念為 (1 234567,?)，標號為1。

2) 畫出形式背景(約簡后)所對應的二部圖G，其屬性中度數最大的頂點為 b ，N(b)={1,3,4,5,6}，故 (1 3456,b)為 (1 234567,?)的直接子概念，標號為21。

3) 畫出 G 的由 P ={1,3,4,5,6}和 N (P)?b={a,c,df,e}導出的子圖 S1，二部圖 S1的屬性集中度數最大的頂點 c ， N (c)={1,4,5,6}，故 (1 456,bc)為(13456,b)的直接子概念，標號為31。

4) 畫出 S1的由 P1={1,4,5,6}和 N (P1)?c={a,df,e}導出的子圖 S2，二部圖 S2的屬性集中度數最大的頂點 a ， N (a)={1,6}，故 (1 6,abc)為 (1 456,bc)的直接子概念，標號為41。畫出 S2的由 P2={1,6}和N(P2)?a={e}導出的子圖 S3，二部圖 S3的屬性集中度數最大的頂點 e ， N (e)={1}，故 (1 ,abce)為(16,abc)的直接子概念，標號為51。此時 P3={1}為單點集，故 (1 ,abce)為倒數第二層概念，其直接子概念只有 (? ,abcdef)， ( ?,abcdef)為最底層概念，標號為6。

5) 從標號為51的概念 (1 ,abce)開始返回到生成它的二部圖 S3，其屬性集中除 e外無其他頂點。所以返回到標號為41的概念 (1 6,abc)的二部圖 S2，其屬性集中除 a 外還有頂點 d f 和 e 。先看 d f，N(df)={5}，未出現過以5為外延的概念，故(5,bcdf)為 (1 456,bc)的直接子概念，標號為42，此時P2?={5}為單點集，故 (5 ,bcdf)為倒數第二層概念，其直接子概念只有 (? ,abcdef)。再看 e ， N (e)={1}，已出現過以1為外延的概念 (1 ,abce)，且其內涵 a bce真包含 b ce，故此處不再考慮。

現在返回到生成標號為31的概念 (1 456,bc)的二部圖 S1，其屬性集中除 c 外還有頂點 a ,df,e。其中N(a)={1,6}， N (e)={1}，已出現過以16和1為外延的概念 (1 6,abc)和 (1 ,abce)，且其內涵真包含 a b和be ，故此二頂點不再考慮。而 N (df)={3,5}，未出現過以35為外延的概念，故 (3 5,bdf)為 (1 3456,b)的直接子概念，標號為32。然后接著畫出 S1的由P1?={3,5}和N(P1?)?df={c}導出的子圖 S2??，二部圖S2??的屬性集中度數最大的頂點為 c ， N (c)={5}，已出現過以5為外延的概念 (5 ,bcdf)，此概念的內涵恰好為 b cdf ，則 (5 ,bcdf)也為 (3 5,bdf)的直接子概念，此頂點不再考慮。

現在返回到生成標號為21的概念 (1 3456,b)的二部圖 G ，其屬性集中除 b外 ，還有 a、 c 、 d f 和 e。其中N(a)={1,6}，N(c)={1,4,5,6}，已出現過以16和1456為外延的概念 (1 6,abc)和 (1 456,bc)，且其內涵真包含 a和 c，故此二頂點不再考慮。 N (df)={2,3,5}，未出現過以235為外延的概念，故 ( 235,df)為(1234567,?)的直接子概念，標號為22。然后接著畫出 G 的由 P?={2,3,5}和 N (P?)?df = {b,c,e}導出的子圖 S1?，二部圖 S1?的屬性集中度數最大的頂點為b，N(b)={3,5}，已出現過以35 為外延的概念 (3 5,bdf)，此概念的內涵恰好為 b df ，則 (3 5,bdf)也為(235,df)的直接子概念，此頂點不再考慮。 S1?的屬性集中除 b 外，還有 c 和 e ， N (c) = {5}，已出現外延為5的概念 (5 ,bcdf)，且其內涵真包含 c df，故此頂點不再考慮。 N (e)={2}，未出現過以2為外延的概念，故(2,def)為 (2 35,df)的直接子概念，標號為33。此時其外延 P1?={2}為單點集，其直接子概念只有(?,abcdef)。

返回二部圖 G 中的屬性 e ， N (e)={1,2,7}，未出現過以127為外延的概念，故 (1 27,e)為(1234567,?)的直接子概念，標號為23。接著畫出G的由P??={1,2,7}和N(P??)?e={a,b,c,df}導出的子圖 S1??，二部圖 S1??的屬性集中 a 、b 、c的鄰集相等，約簡后屬性集中度數最大的頂點為 a bc 和 d f ， N (abc)={1}，N(df)={2}，已出現過以1和2為外延的概念(1,abce)和 (2 ,def)，其內涵恰好為 a bce 和 d ef，則(1,abce)和 (2 ,def)也為 (1 27,e)的直接子概念，此二頂點不再考慮。

到此已生成所有概念，見圖4。其概念格見圖3。

圖4 生成概念格的過程Fig. 4 Process of generating concept lattice

4 結束語

本文結合圖論的內容，將概念格的形式背景和一個二部圖相對應，利用二部圖的極大完全子圖來尋找概念，并且同時得到概念之間的父子關系，最終構造出概念格。此方法同時生成Hasse圖，簡單直觀，能夠快速生成概念格。基于概念格的形式背景與圖論內容的高度關聯性，二者之間其余理論的相互應用是我們下一進努力的方向。