非線性布爾網絡系統模糊建模與動態性能分析

呂紅麗，宋玉晶，段培永

1965年，Zadeh[1]首次提出基于模糊集合的模糊數學概念。1974年，Mamdani[2]首先將模糊數學理論應用于工業控制中，實現了對鍋爐和蒸汽機的模糊控制，使模糊控制從理論走向實際應用。1985年，日本學者Takagi等[3]又提出了以線性精確數學表達式為模糊規則后件的T-S模糊模型，將模糊控制系統與線性控制系統有效地結合起來。隨后國內外學者基于T-S模糊模型，研究了非線性系統的大量控制問題，得到了豐富的模糊控制理論研究成果[4-9]。在T-S模糊模型的基礎上，Feng等[5-6]提出了模糊動態模型(fuzzy dynamical model)。其主要思想是，構造一組線性模型，分別描述系統的動態特性，通過局部線性模型的加權組合得到系統的全局非線性動態模型。文獻[10]中提出了一種離散時間模糊控制系統，將非線性離散時間系統作為模糊控制系統的后件部分，分析了系統的動態性能。

1969年，Kauffman[11]首先提出布爾網絡模型，布爾網絡是關于布爾狀態變量的一種簡單的邏輯動力系統，是當前學者專家們共同關心的熱點問題。針對布爾網絡研究缺少有效的數學工具問題，程代展教授在文獻[12]中首次提出矩陣半張量積方法。這種方法將邏輯運算轉換成代數運算，使得許多經典的處理量變過程的數學工具可直接用來分析邏輯動態系統。在文獻[13]中，程代展教授將這種方法應用于布爾網絡，將邏輯動態控制系統轉化為普通離散時間系統，提出了一系列關于布爾網絡的新理論。隨后在文獻[14-17]中研究了布爾網絡系統的能控能觀性等性質，形成了布爾控制網絡分析設計的完整理論框架。之后，學者們在控制理論方面對線性布爾網絡系統做了大量的深入研究[18-23]，但是沒有針對非線性布爾網絡系統進行分析和研究。

為了解決非線性布爾網絡的數學建模與分析問題，利用模糊動態模型的非線性特點，將模糊動態模型和布爾控制網絡相結合，建立了模糊動態布爾網絡系統的局部模型和全局模型，并且分別分析了系統局部模型和全局模型的能控性、能觀性和穩定性。

1 預備知識

1.1 數學符號說明

為了敘述方便，文中用到的記號列表如下：Mm×n表示所有 m ×n矩 陣的集合，?表示矩陣的張量積 ； Col(A)(Row(A))為 矩 陣 A 的 列(行)集 合 ；Col(Ai)(Row(Ai))為矩陣 A 的 第 i 列(行)；記 δin是單位矩 陣 In的 第i 列 ； Δn=δin|i=1,2,···,n；Dk={0,1,···,k?1},k≥2。記邏輯變量：真 ～ T?1，假 ～ F?0，則D={0,1}；f:Dn→D 稱 為 邏 輯 函 數 ； L ∈ Mn×r,稱L 為邏輯矩陣，如果 C ol(L)? Δm,m×r維邏輯矩陣全體記為 Lm×r；設矩陣 L ∈ Mn×r。其[中， C ol(L)]? Δn,稱L 為邏輯矩陣，可簡記為 L =δni1i2···ir；矩陣B ∈ Mm×n為 布 爾 矩 陣 ， 如 果B中(bi,j)∈D,m×n維布爾矩陣全體記為 Bm×n。

1.2 模糊動態模型

模糊動態模型是非線性復雜系統模糊建模中一種典型的模糊建模方法。模糊動態模型每條規則的后件部分是一種狀態空間形式的局部線性系統，因此對于局部的線性模型可以采用線性系統的理論體系去研究，然后通過模糊推理得到全局意義下的模糊控制系統的分析和設計。

一個m個輸入n個輸出的非線性系統，其模糊s控制器可表示為 Σ ∈ f(y1×y2···×yn× x1× x2···× xm)，其中 {xi}是模糊控制器的輸入，論域為 Exi, { yi}是模糊控制器的輸出，論域為 Eyj。將模糊變量 xi,yj按照隸屬度函數進行模糊化, Exi={xi1,xi2,···,xiαi},i=1,2,···,m，分別對應于“負大”“負中”·· ·是基于隸屬度的模糊集 合 ； Eyj={y1j,y2j,···,yβjj},j=1,2,···,n,分 別 對 應 于“負大”“負中”·· ·是基于隸屬度的模糊集合。

假設總共有 N 條模糊規則，則第 k條模糊規則為 Rk, k =1,2,···,N，其模糊規則為

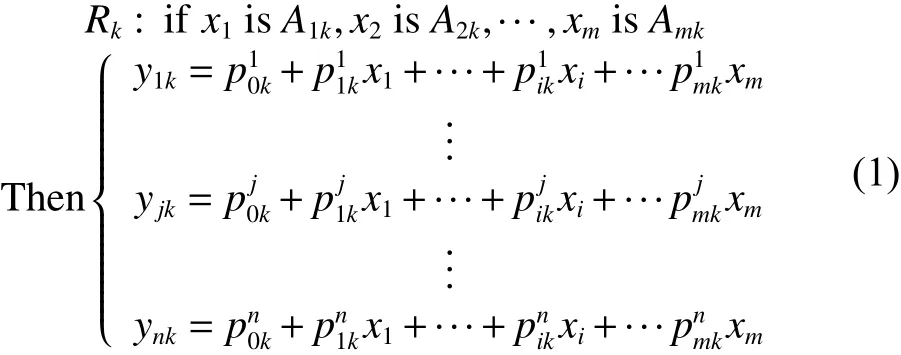
式中： Aik是一個模糊集合； yjk是第 k條模糊規則的第 j 個輸出， j =1,2,···,n ；是第 k條模糊規則結論中第 j 個輸出的線性多項式函數中變量 xi項的系數，一般為常數項，特別的通常可以歸一化為1。

對 于 第 k 條 規 則 Rk，如 果 已 知 輸 入x1=x?1,x2=x?2, ···,xm=x?m,則 在結 論部 分的 輸出 yjk可 以由線性多項式函數計算得到：

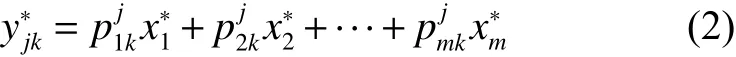
每條規則的激活度 μi為

式中： μAik(x?i)表示論域中第i 個元素對 Aik的隸屬度，∧是取小運算。

模糊動態模型的輸出 yj是由所有 k條規則(k=1,2,···,N )的輸出加權平均得到的。模型的輸出為

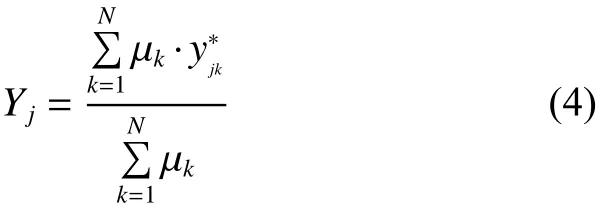
1.3 邏輯的矩陣表示

矩陣的半張量積是中科院系統所程代展教授在文獻[12]中提出的一種新的矩陣乘法，即設A ∈ Mm×n,B ∈ Mp×q：

1)如果 n =p,則稱A與B滿足等維數關系；

2)果 n =tp (記為 A ?tB )，或者)，則稱 A與 B滿足倍維數關系，否則稱一般維數關系。矩陣乘積在倍維數關系下的一種推廣如定義1。

定義1[13]設 X 為 n =pq 維行向量,Y 為 p 維列向量。將X等分成 X =(X1,X2,···,Xp)，這里Xi∈Rq,i=1,2,···,p 。那么， X 和 Y 的半張量積記作X?Y,定義為一個行向量：

類似的，

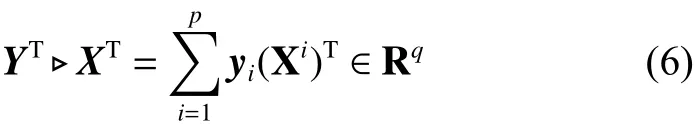
為一列向量。

普通矩陣乘法是半張量積的特殊形式，普通矩陣乘法具有的性質，對于半張量積幾乎都成立，此外還具有一些特有的性質。

定理1[13]設 f (x1,x2,···,xn)為一個邏輯函數，在向量形式下 f :Δ2n→ Δ則存在唯一的邏輯矩陣Mf∈ L2×2n，稱為 f的結構矩陣，使得

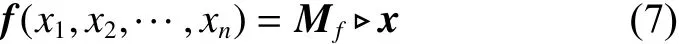
式中 x =?ni=1xi。常用的邏輯算子及其結構矩陣分別為

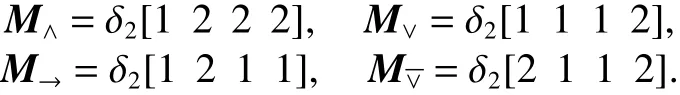
1.4 布爾 (控制)網絡

定義2[13]1)布爾網絡的動態方程為

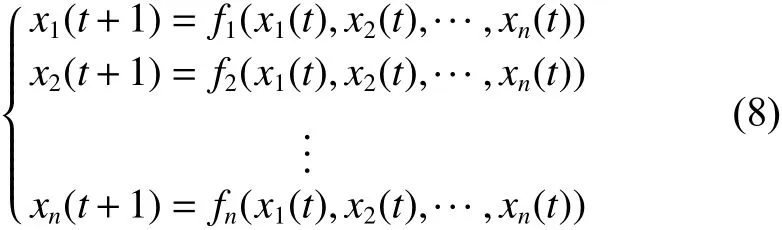
式中： fi:Dn+m→ D,i=1,2,···,n;為邏輯函數；xi(t)∈D,i=1,2,···,n為狀態變量。

2)布爾控制網絡是指一個含有輸入輸出的布爾網絡，其動態方程為

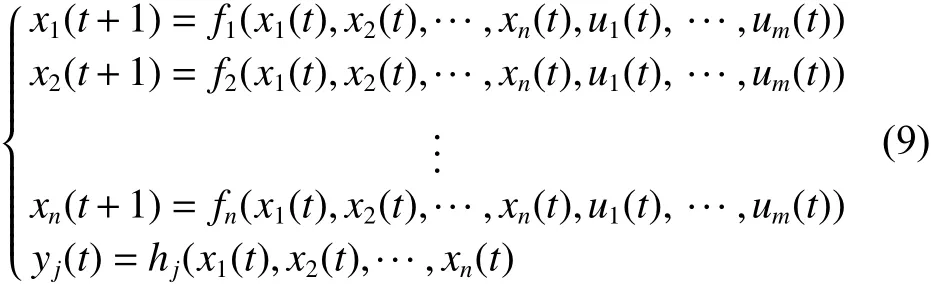
式 中 ： xi(t)∈D, i = 1,2,···,n 為 狀 態 變 量 ；ui(t)∈D,i=1,2,···,m 為控制變量； yi(t)∈D,i=1,2,···,p為輸出變量；fi:Dn+m→ D,i=1,2,···,n;hi:Dn→ D,i=1,2,···,p 為邏輯函數。

定理2[13]利用向量表達式

1)布爾網絡的動態方程式(8)可表示為

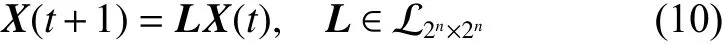
2)布爾控制網絡的動態方程式(9)可表示為

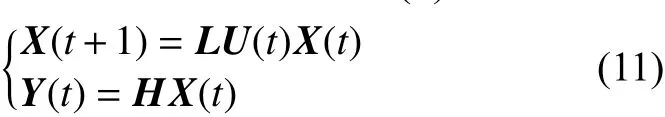
2 非線性布爾網絡系統的基本概念

定義3 1)一個多輸入多輸出的非線性布爾網絡系統可以表示成模糊動態布爾網絡模型(fuzzy dynamic Boolean network model，FDBNM)，即

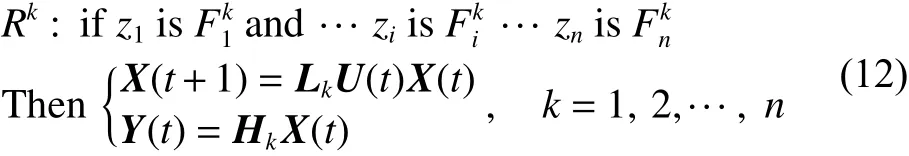
簡記為

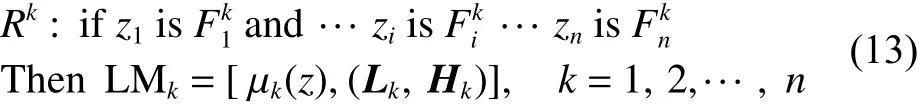
2)第 k個FDBNM為

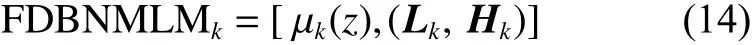
式中： μk(z)是模糊推理集合 Fk的隸屬函數；Fk=(Lk,Hk)為局部模型的結構矩陣， ( Lk,Hk)也稱為FDBNM的第 k個子系統。

這里,Rk,k=1,2,···,N 為系統的第 k條模糊規則，也稱為第 k個模糊子系統，N為總的模糊規則數； z1,z2,···zn為規則前件語言變量；為模糊集，其隸屬度函數設為三角形函數，記作；(X(t+1),Y(t))是系統的輸出； U (t)是輸出部分布爾控制網絡的控制變量； ( Lk,Hk)為系統的結構矩陣。

對 給 定的輸 入 信 號 z1=z?1,z2=z?2,···,zn=z?n,利用三角形隸屬函數將其模糊化，對每條規則的激活度采用max-min方法：

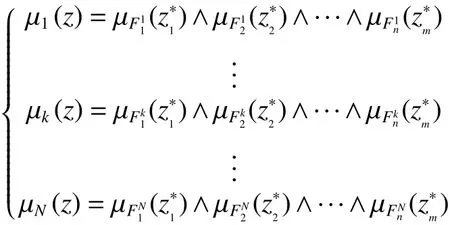
3)使用加權平均法解模糊，可得FDBNM的全局模型為

簡記為

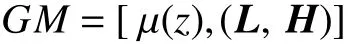
定義4 1)對于模糊動態布爾網絡控制系統的局部模型式(14)， G 固定，如果存在控制變量，能使方程式(14)從初始狀態 X (U,0)=X0到達終端狀態 X (U,t)=Xd,則稱 Xd從 X0經過t步是能控的。如果存在控制變量 U ,使式(14)能從任意初始狀態到達 X (T)=Xd，則稱模糊動態布爾網絡控制系統的局部模型是能控的。

2)對于模糊動態布爾網絡控制系統的全局模型式(15)，如果存在控制變量 U0，能使方程式(15)從初始狀態 X (U,0)=X0到達終端狀態,則稱 Xd從 X0經過t步是能控的。如果式(15)能從任意初始狀態 X0到達 X (T)=Xd，則稱模糊動態布爾網絡控制系統的全局模型是能控的。

定義5 1)對于模糊動態布爾網絡控制系統的局部模型式(14)，對任意給定的初始狀態如果至少存在一個布爾控制序列，使初始狀態能由輸出序列唯一地確定，則稱局部模型是狀態能觀測的。

2)對于模糊動態布爾網絡控制系統的全局模型式(15)，對任意給定的初始狀態如果至少存在一個布爾控制序列，使初始狀態能由輸出序列唯一地確定，則稱全部模型是狀態能觀測的。

定義6 1)對于模糊動態布爾網絡控制系統的局部模型式(14)，如果經過固定步數，存在一個不動點 Xe，使得對于局部模型的任意的初始狀態都有，則稱系統的局部模型是能穩定的。

2)對于模糊動態布爾網絡控制系統的全局模型式(15)，如果經過固定步數，存在一個不動點Xe，使得對于全局模型的任意的初始狀態都有, 則稱系統的全局模型是能穩定的。

3 非線性布爾網絡系統動態性能分析

系統局部模型的布爾控制網絡系統(14)的結構矩陣可以等分為 2m塊[13]，即

式中： B lki(Lk)是矩陣 Lk的第i 個 n ×n的 塊； Bi∈ L2n×2n，i=1,2,···,2m。令

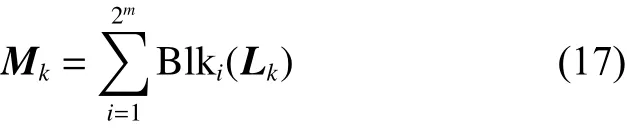
3.1 能控性

首先引用布爾矩陣的布爾乘法及布爾冪的定義[13]。

1)設 α ,β,αi∈ D,i=1,2,···,n ， 則 布 爾 加 法 定義為

2)設 A =(aij)∈ Bm×n,B=(bij)∈ Bn×p，則布爾乘法定義為

3)設 有定義，則布爾冪定義為A?A

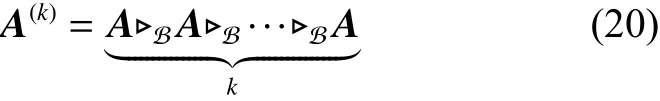
對于模糊動態布爾網絡控制系統的局部模型式(14)，定義能控性矩陣為[13]

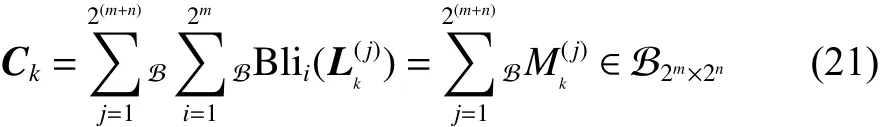
定理3 1)當且僅當矩陣 Ck＞0時，局部模型式(14)是能控的。

2)當且僅當矩陣 C ＞0時，全局模型式(15)是能控的，即

證明 通過數學歸納法來證明。

當 j =1時，由式(17)知，當 Mk＞0時，存在一個控制序列使狀態 X0到 Xd,顯然局部模型式(14)是能控的；假設當 j =k′時，式(14)能控 ，則 當 j=k′+1時因為Mk＞0,可知 Ck＞0，且存在控制序列使局部模型式(14)能控。

3.2 能觀性

為了找到能觀性矩陣，對于第k個局部模型，定義一組矩陣集合[13]:?ki∈ L2p×2n,i=0,1,2···其表達式為

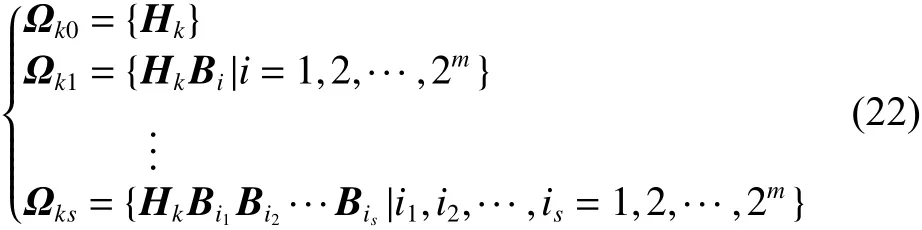
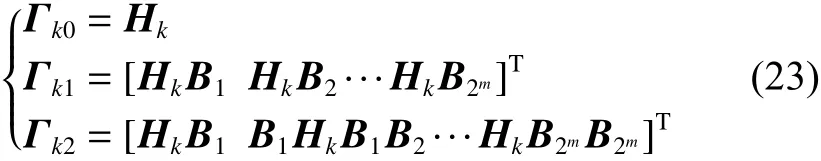
令

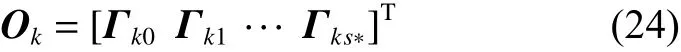
式中 Ok稱為系統局部模型式(14)的能觀測矩陣。

定理4 1)設系統局部模型式(14)是能控的，那么局部模型式(14)是能觀的，當且僅當

2)設系統全局模型式(14)是能控的，那么全局模型式(17)是能觀的，當且僅當

證明[16]對給定的狀態 X0，可以觀測 H X0，因為系統是能控的，所以使用不同的控制序列 Ui，可以觀測 H LUi，故 H LUi1LUi2···LUisX0是可觀測的。因為 s ≥k0，沒有增加之前集合的線性獨立的行數，線性獨立行數對初始狀態的辨識是無用的，只有當包含所有不同列，即時，初始狀態才能辨識，全局模型是能觀測的。

3.3 穩定性

對于布爾系統式(8)和布爾控制系統式(9)記χ=Dn為它們的狀態空間。點 X ∈χ可以表示為X=[x1,x2,···,xn]T,邏輯映射 F :χ → χ，邏輯映射形式為[13]

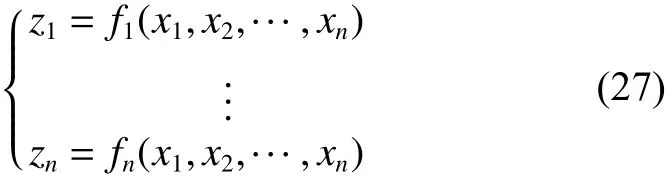
簡記為 Z =F(X),X ,Z∈χ。

定義7[13]邏輯映射 F 的關聯矩陣 I( F)=(bij)是一個 n ×n矩陣，定義為

記X=[x1,x2,···,xn]T,F=[f1,f2···,fn]T，則式 (14)對應的布爾網絡的邏輯映射可簡記為

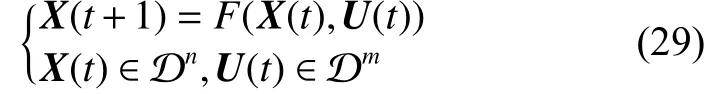
同理式(15)對應的布爾控制網絡的邏輯映射可簡記為

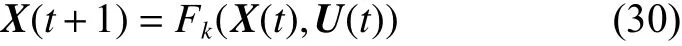
式中 X (t)∈Dn,U(t)∈Dm。

定理5[13]1)設 ξ是式(14)的一個不動點，則X(k)∨ˉξ≤I(Fk)j×(X(0)∨ˉξ),如 果 存 在 j ＞0,使 得[I(Fk)](j)=0，則稱局部模型是能穩定的。

2)設 ξ 是式(15)的一個不動點，則X(k)∨ˉξ≤I(F)j×(X(0)∨ˉξ),如果存在 j ＞0,使得 [I (F)](j)=0，則稱全部模型是能穩定的。其中

證明[14]①必要性：如果系統的局部模型是穩定的，即系統是收斂的，則 T 步后(T為極短的時間段)，所有的狀態收斂到 ξ，所以當 j ＞T時成立。

②充分性：假設存在 j ＞0,使 [I (Fk)](j)=0成立，那么對于任意的 X 有 Fkj(X)=ξ， X (t)∈Dn。故對任意步數 t ≥j,Fkt(X)=Fkj(Fkt?j(X))=ξ ，得證。

同理可證全局模型時系統的穩定性。

4 實驗仿真

根據第3節介紹的模糊動態布爾網絡控制系統，本節選取多輸入多輸出模糊模型進行非線性模糊建模及其能控性、能觀性分析。

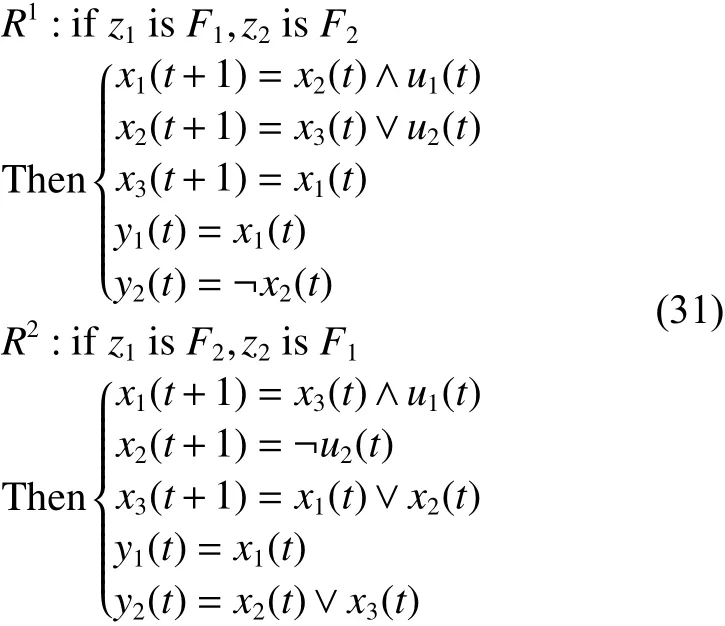
其代數表達式為

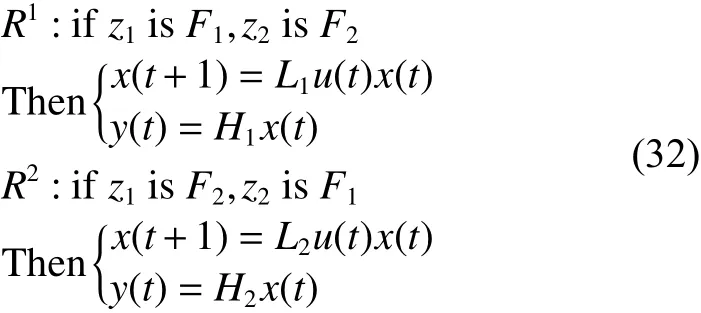
則整個系統模糊狀態方程可表示為式(15)，其中

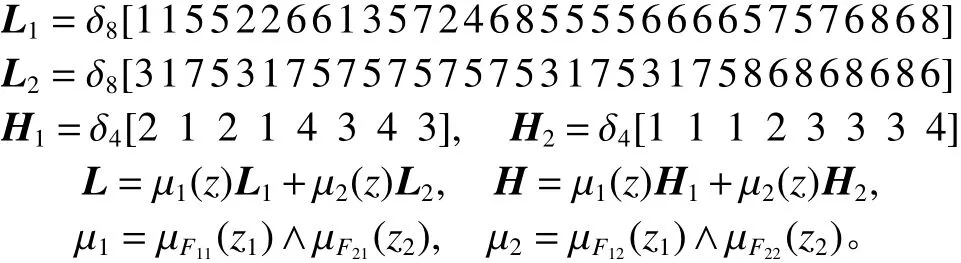
由選取的模糊模型，規則1和規則2時的狀態變量、輸入變量和輸出變量的初始狀態可分別設為

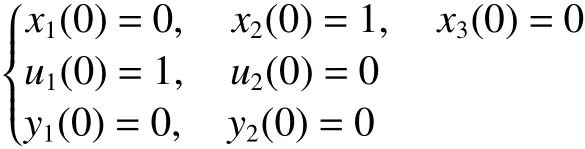
4.1 能控性

由式(16)，將規則1時的結構矩陣等分為4塊：

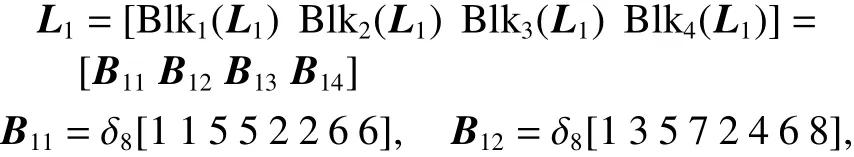
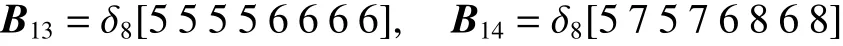
則

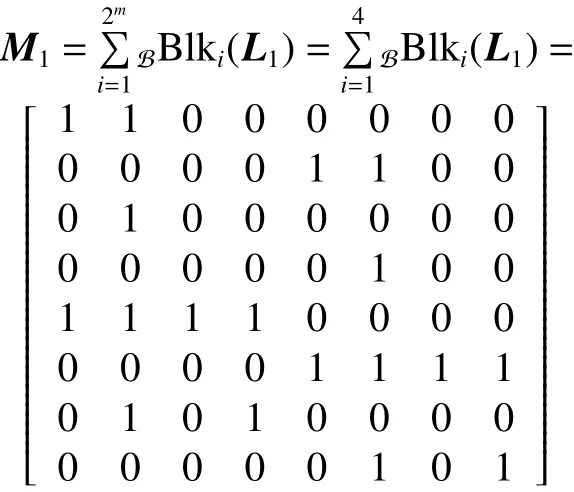
其能控性矩陣為

故規則1時的局部模型是可控的。

由MATLAB仿真知，規則1時控制變量和狀態變量的關系如圖1(a)所示。

同理，規則2時有：

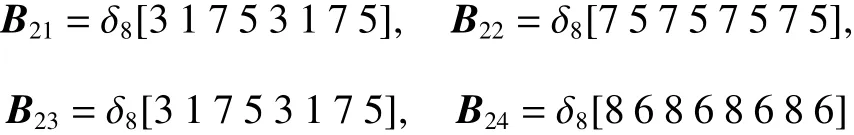
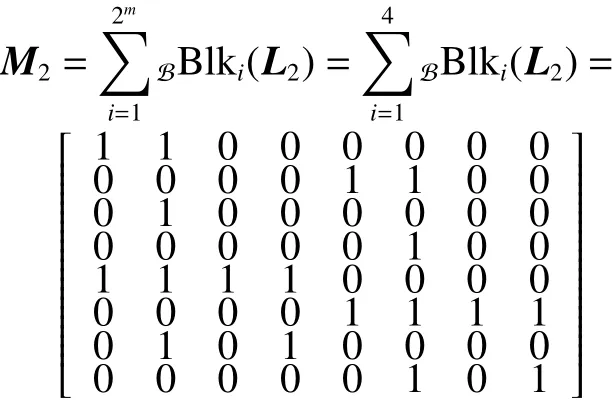
其能控性矩陣有

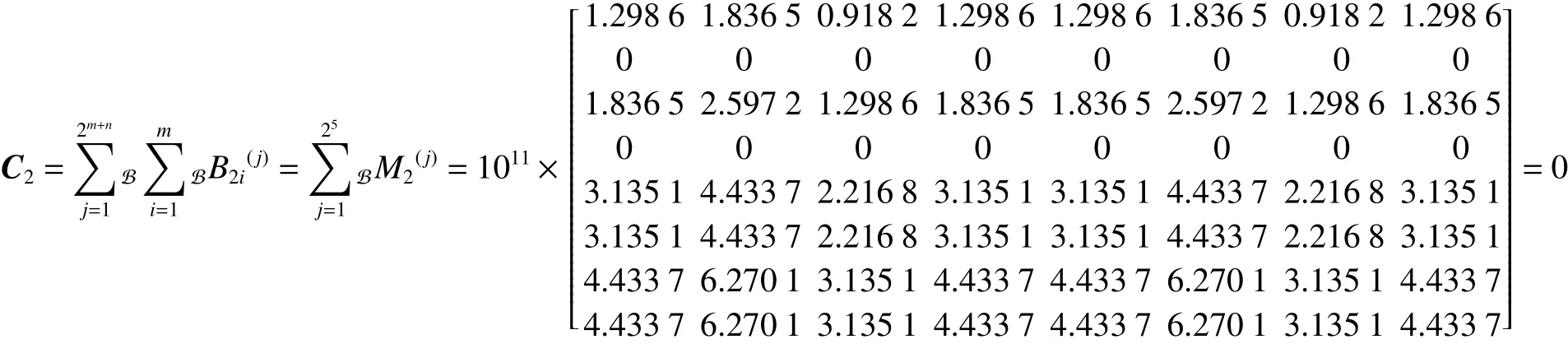
故規則2時的局部模型是不可控的。

由圖1可知，規則1時的局部模型是可控的，規則2時的局部模型是不可控的，與實驗計算結果是一致的。

4.2 能觀性

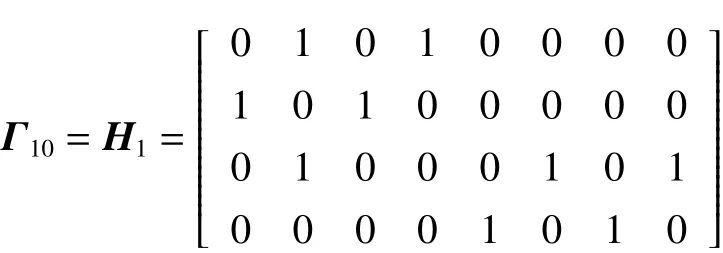
Γ12為64×8維的布爾矩陣，由于篇幅的限制，上式中只列出了一部分。

Γ13為256×8維的布爾矩陣，由于篇幅的限制，上式中只列出了一部分。

O1為340×8維的布爾矩陣，由于篇幅的限制，文中只列出了一部分。

可得，Rank (O1)-7＜23=8。

由MATLAB仿真知，規則1時輸出變量和狀態變量的關系如圖2所示。由圖2知，雖然規則1時的局部模型是能控的，但是是不能觀測的；規則2時的局部模型是不可控的，故也是不能觀測的，與實驗計算結果是一致的。

4.3 穩定性

規則1時，式(33)對應的布爾網絡的邏輯映射為 X (t+1)=F1(X(t)),X∈D3。

關聯矩陣為

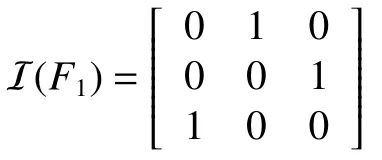
[I(F1)](5)=I(F1)≠0， 即 [I (F1)](k)≠0,則 規 則1下的局部模型是不穩定的。

規則2時，式(31)對應的布爾網絡的邏輯映射為 X (t+1)=F2(X(t)),X∈D3。

關聯矩陣為

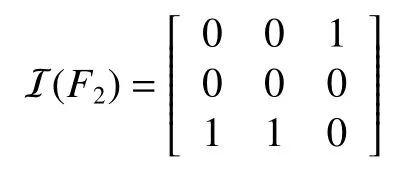
[I(F2)](3)=0，則規則2下的局部模型是穩定的。

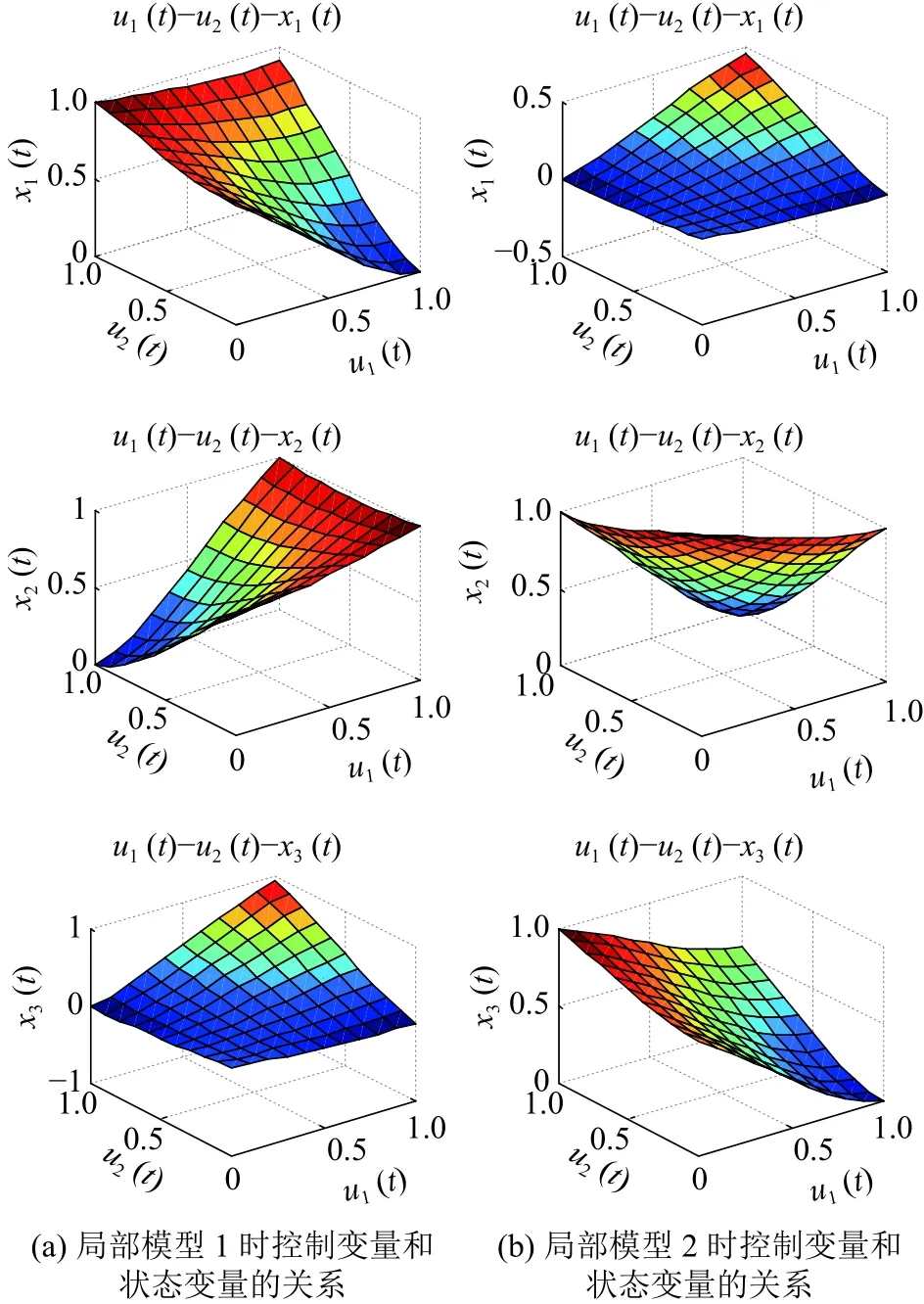
圖1 控制變量和狀態變量的關系Fig. 1 Schematic diagram of relationship between the control variables and state variables

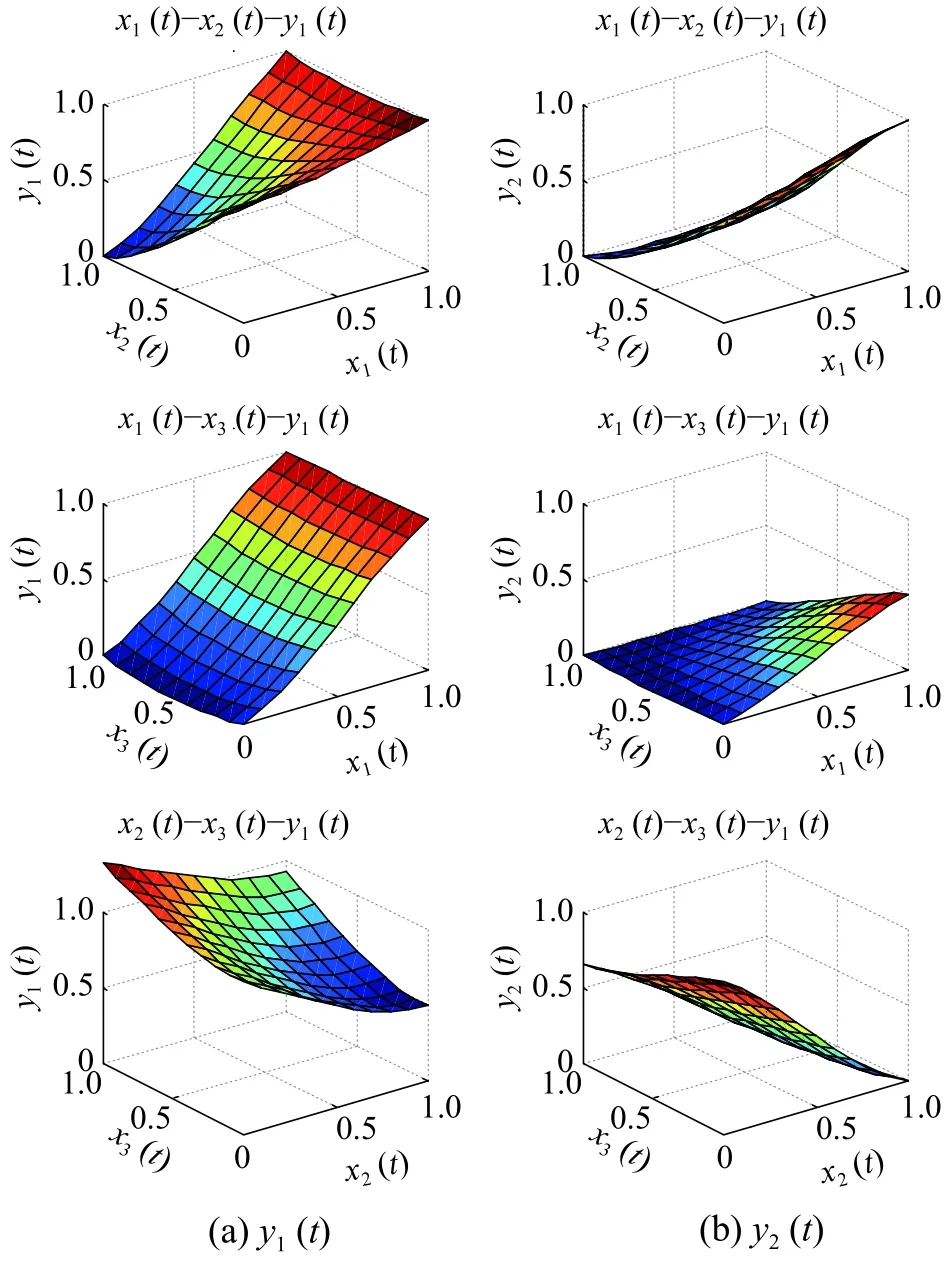
圖2 輸出變量和狀態變量的關系Fig. 2 Schematic diagram of relationship between the output variables and state variables under rule 1

綜上分析，整個系統模糊狀態方程可表示為式 (15)，其中，取 μ1=1,μ2=0,則L=L1,H=H1,F=F1,C=C1＞0,Rank(O)=Rank(O1)=7＜23=8, 因此系統的全局模型是能控不能觀且不穩定的。

5 結束語

通過具體實例仿真分析可知，對于布爾網絡系統，可以實現非線性模糊建模和動態性能分析。利用模糊動態模型的非線性特點，將模糊動態模型和布爾控制網絡相結合，分別建立了模糊動態布爾網絡控制系統的局部模型和全局模型，并且對其能控性、能觀性和穩定性進行了分析。