采煤機搖臂傳動系統的優化設計

任 聰

（山西霍爾辛赫煤業有限責任公司， 山西 長治 046600）

引言

搖臂作為采煤機械工作時的動力傳動部件，其可靠性直接影響著采煤機是否能夠正常工作，因采煤機位于一線綜采面，其工作環境極端的惡劣使采煤機的搖臂傳動系統經常會因劇烈震蕩或者過載而受到損害，嚴重影響著煤礦的正常生產，因此對采煤機的搖臂傳動系統進行優化設計，提高其工作的可靠性具有重大的意義。

1 搖臂傳動系統的可靠性模型

以某采煤機的搖臂傳動系統為研究對象，其傳動系統主要由一個一級行星減速系統及一個三級直齒輪減速系統構成，根據其結構組成，其搖臂傳動系統的可靠性模型如圖1所示。

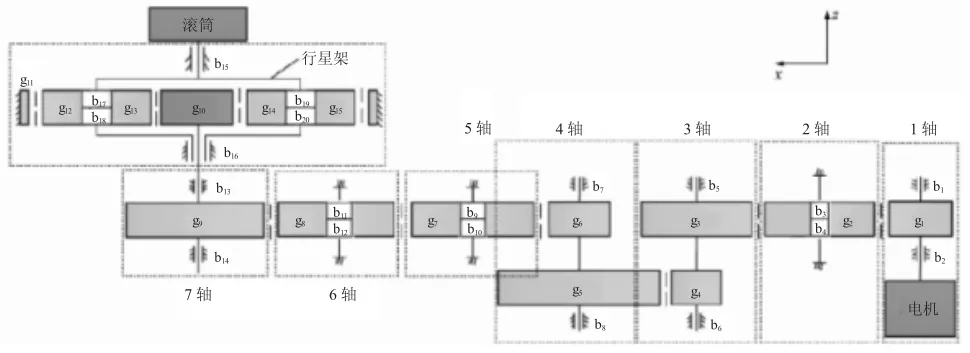
圖1 搖臂傳動系統的可靠性模型

整個系統的運動學方程可表述為[1-2]：

式中：M為傳動系統的質量矩陣；A為阻尼矩陣；k為剛度矩陣；u為系統的節點位移向量；Fu為外激勵向量。為了便于對其運動學方程進行分析，利用瑞利阻尼確定黏性阻尼項Cs，其表達如下：

其中：

式中：ω1、ω2分別為搖臂傳動系統的第一階和其第二階轉速，ξ1、ξ2則分別為其對應的第一階和第二階的模態阻尼比。

2 搖臂傳動系統的疲勞可靠性模型

采煤機工作狀態是切割下來的小碎屑狀的煤塊與大塊狀的煤塊交替掉落的過程，且無規律可循，在這個交替沖擊的過程中會不斷引起采煤機的截齒載荷不規律的波動，進而導致采煤機滾筒端部所承受的載荷是隨機波動的載荷[3]。假設采煤機工作的煤層為中硬度的煤層，根據破煤理論的相關知識及現場試驗測得的試驗數據，可計算出搖臂傳動系統行星架端部的隨機載荷的大小，如圖2所示。

圖2 行星架端部的隨機載荷大小的變化情況

將圖2所示的隨機載荷施加到建立好的采煤機搖臂傳動系統的有限元分析模型中，可得出采煤機搖臂傳動系統在工作情況下危險部分的應力圖譜，然后根據齒輪的S-N曲線可計算得出傳動齒輪的疲勞壽命，對試驗得到的樣本進行分析，可得出搖臂傳動系統的壽命N關于其結構參數的關系式[4]：

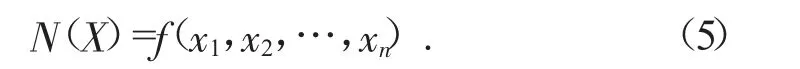
式中：X為傳動系統的基本隨機變量。

由此可得出傳動系統的疲勞壽命的函數g（X）為：

式中，N0為傳動系統的設計壽命。

3 搖臂傳動系統可靠性優化

搖臂傳動系統中的結構參數對于傳動系統整體的疲勞壽命有著顯著的影響作用，因此為了保證搖臂傳動系統工作的可靠性，必須依靠穩健優化的思想對其進行優化，其優化設計的數學模型可以用數學模型進行表述：

由于齒輪的中心距會影響到搖臂工作時候的采高范圍，而且齒輪的壓力角對于系統結構的疲勞壽命影響不大，因此只需對齒輪g1和行星輪齒寬、變位系數等參數進行優化，即：

式中：B1為齒輪g1的齒寬；B2為行星輪的齒寬；X1為

齒輪g1的變位系數；X2為行星輪的變位系數。

3.1 基于可靠度的目標優化方案（方案1）

方案1的數學表達式為：

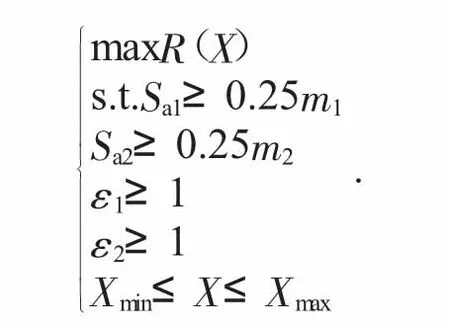
式中：Sa1為齒輪g1的齒頂厚度；Sa2為太陽輪的齒頂厚度；ε1為齒輪g1的重合度；ε1為行星輪的重合度；m1為齒輪g1的模數；m2為行星輪的模數。方案1能夠確保各結構設計參數都能在限定的值范圍內，齒輪的嚙合度大于1并且齒頂厚度大于經驗數值時，對搖臂系統的結構參數進行合理的優化。

3.2 基于靈敏度的目標優化方案（方案2）

方案2的數學表達式為[5]：

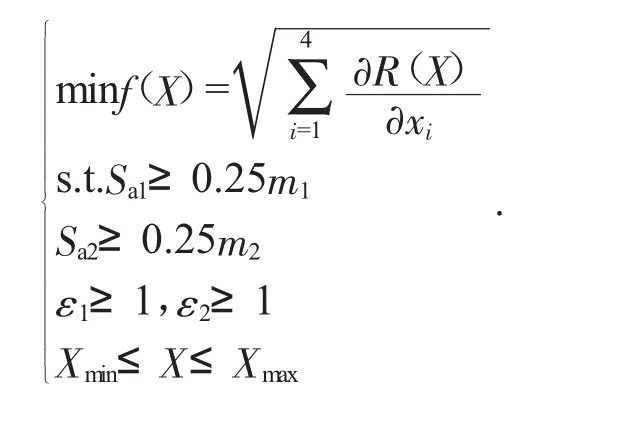
方案2是用搖臂運動系統的疲勞壽命的可靠度相對于其他參數的靈敏度來作為目標函數。

3.3 基于可靠穩定性的的優化方案（方案3）

方案3的數學表達式為：

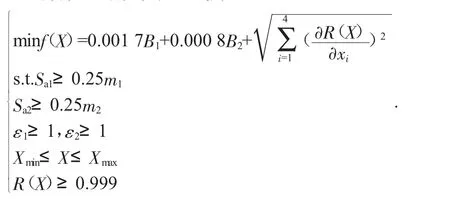
方案3是在綜合考慮了齒輪各影響因素的基礎上對系統的質量、穩定性、可靠性等進行的優化，相關因素考慮更為全面也更為接近于搖臂運動機構的實際工作狀態。

對以上3種優化方案，利用Matlab優化工具箱編制分析程序，分析結果如圖3所示。

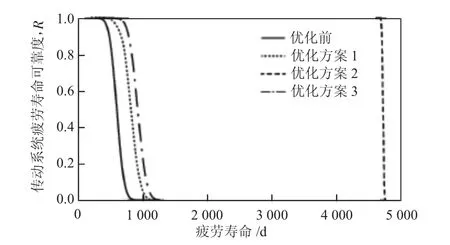
圖3 疲勞壽命可靠度對比曲線

由分析結果可以看出采用方案3，基于可靠穩定性的優化方案能夠大幅提高搖臂系統的抗疲勞強度。

4 結論

本文提出的基于可靠穩定性的優化方案，能夠在保證系統可靠性的前提下大幅提高系統工作的穩定性，對采煤機搖臂傳動系統的可靠性、穩定性的提升具有重大意義。