水工隧洞不同圍巖等級力學性能研究

王 順，賈 飛

(1.河北工業大學土木與交通學院，天津300401;2.西安理工大學水利水電學院，陜西西安710048)

隧洞是水工建筑物中極其重要的結構形式之一，特別是在水利工程的輸調水工程中。有些隧洞長度要達數十公里，埋深在幾千米之內，要穿越很多種不同的地質單元，遇到松散地層、斷層破碎帶、淺埋強風化、溶洞等地質情況。隧洞工程的工序繁多、技術復雜、施工比較困難，往往成為整個水利工程的控制性工程[1- 3]。隧洞的圍巖穩定及支護結構安全是保證隧洞安全、實現隧洞功能的關鍵因素[4- 6]。深埋地下隧洞工程具有工作年限長、工程規模大、工程重要性等級高等特點，一旦引發圍巖的穩定性問題將會給工程帶來災難性的破壞。因此，深入分析隧洞襯砌結構的穩定性，準確模擬隧洞圍巖與支護結構的變形、應力特點，并對圍巖條件差的危險洞段進行鋼拱架結構整體加固，是許多學者和工程技術人員研究的熱點[7- 10]。

針對隧洞的研究已取得了一定的成果，但大多局限于單一類型圍巖，然而在實際的工程環境中，有些地區地質條件復雜，圍巖等級明顯下降。因此，探究圍巖等級下降時對水工隧洞內力及變形產生的影響，有助于確保圍巖穩定及施工安全，為同類工程提供參考。

1 研究方法

1.1 工程概況

某土建工程主要有攔河壩、連接洞、取水口、低壓引水洞、調壓井、壓力豎井、壓力鋼管、地面廠房、尾水洞和進場公路。工程的基本特征要素如下：總水頭233 m，凈水頭194.40 m，設計流量26.0 m3/s，裝機容量48 MW(4×12 MW)，設計洪水位1 836 m，最高運行水位1 835.9 m，最低運行水位1 832.0 m。

該工程從取水口到沉沙池的連接渠道長約80 m。渠道采用低壓引水隧洞，洞長3 850 m，布置在左岸，鉆爆法施工，進口底高程(沉沙室后)1 818.7 m，出口底高程(接調壓井)1 804.0 m，最大埋深500 m，最小埋深40 m。進口和過溝拐點位置各布置1個施工支洞。引水隧洞斷面呈城門洞形，頂拱半徑1.5 m，底寬3.6 m，側墻高2.3 m。

根據GB 50086—2001《錨桿噴射混凝土支護技術規范》中不同圍巖級別劃分可知[11- 12]，該工程涉及到Ⅲ類圍巖和IV類圍巖。其中，Ⅲ類圍巖主要為層間結合良好的薄層和軟硬巖互層結構，以構造節理為主，節理面多數閉合，層間結合良好，約占總體圍巖1/3；IV類圍巖主要為層間結合不良的薄層和中厚層以及軟硬巖互層結構，部分張開層間有泥質填充，多數夾泥層間錯動明顯，結構結合能力相對較差，約占總體圍巖的2/3。

1.2 計算原理

Abaqus軟件擁有能夠真實反映圍巖性狀的本構模型，能夠平衡初始地應力，可以精確模擬接觸面的性狀等優點，并提供了解決復雜接觸關系的接觸面模擬功能，對巖土工程有很強的適應性[13]。由于計算要考慮到錨桿、地層變形和地層塑形應變，本次采用地層結構法進行分析計算。

初始自重應力場通常可以用有限元方法得到，但必須滿足平衡條件和屈服準則，工作量大，可能不收斂。鑒于丁文其[14]等提出新的方法在沉管中平衡地應力是可行的，此次應用于斷面更大的隧洞中，探究其方法的可行性。首先將重力荷載施加于圍巖，并根據實際工程施加邊界條件，通過計算得到重力荷載作用下的應力場，再將應力場導出重新定義為初始應力場，和重力荷載一并施加到原有限元模型中，即可得到初始應力場。在保證各節點初始位移為0的同時，既滿足平衡條件，又不違背屈服準則。

本次模擬施工采用軟化模量法。在支護和襯砌施工前，先將待開挖區單元的彈性模量降低(本方案中降低40%)，再根據施工順序，依次模擬應力釋放效應，噴錨支護的施加，最后再添加襯砌。

1.3 研究內容

本次模擬研究以引水隧洞為分析對象，主要包括：①利用丁文其等提出的方法進行地應力平衡，探究其方法用于隧洞的可行性；②基于Abaqus計算Ⅲ類和IV類圍巖等效位移、等效塑性應變、支護水平位移、支護豎直位移、支護軸力、支護彎矩和錨桿軸力，根據Abaqus計算云圖，取計算結果的最大值，描述其變化規律，分析最大內力及應變出現的原因；③就Ⅲ類和IV類圍巖計算結果進行對比分析，對內力及變形突出位置加以加固與防護，并提出相關建議，達到優化設計，安全穩定的目的。

1.4 計算假定

假定如下：①材料變形性質假定為各向同性；②圍巖按摩爾-庫倫理想彈塑性模型考慮，混凝土及錨桿按線彈性模型考慮；③初始應力場僅考慮自重作用；④不考慮地下水在開挖過程中的作用。

2 模型計算

2.1 計算工況及參數

本文對Ⅲ類和Ⅳ類圍巖采取相同的計算工況，即支護厚度15 cm，錨桿長度4 m，襯砌厚度30 cm，主要考慮圍巖垂直松動壓力、側向松動壓力、襯砌自重等荷載作用，進行有限元應力變形計算。根據工程地質勘察及設計成果，選取圍巖、噴射混凝土、混凝土底板、二次襯砌、錨桿的材料參數。計算參數見表1。

2.2 計算方法

本次模擬隧洞計算模型坐標規定為：X軸為斷面水平方向，向右為正；Y軸為斷面豎直方向，向上為正；模型的左、右兩側為水平位移約束，上、下邊界為垂直位移約束。為了更契合實際工程，IV類和Ⅲ類圍巖分別打5根、7根錨桿。模型采用四邊形單元進行網格剖分，模型共7 878個節點、7 802個單元。圍巖采用平面單元模擬，支護、襯砌和錨桿采用梁單元模擬，計算范圍是8倍的洞徑。地層結構法模型見圖1。

圖1 地層結構法模型

3 結果分析

3.1 圍巖變形

等效位移是3個方向的位移矢量和，是總位移，而且是相對位移。Ⅲ類和IV類圍巖等效位移分布見圖2。從圖2中可以看出，Ⅲ類和IV類圍巖等效位移分布圖都是左右對稱分布，最大位移都出現在隧洞底板中部，最大值分別為3.79×10-4、6.02×10-4m。

圖2 等效位移分布(單位：m)

等效塑性應變描述整個變形過程中塑性應變的累積結果。Ⅲ類和IV類圍巖等效塑性應變分布見圖3。從圖3中可以看出，Ⅲ類和IV類圍巖等效塑性應變分布圖都是左右對稱分布，區域數值大于0的地方，表示材料已經屈服。Ⅲ類和IV類圍巖最大塑性變形都出現在隧洞兩側中部，最大值分別為3.03×10-4、2.25×10-4，數值較小，未超過材料的破壞應變。

圖3 等效塑性應變分布

3.2 支護內力及變形

Ⅲ類和IV類圍巖支護水平位移見圖4。從圖4可知，Ⅲ類和IV類圍巖支護水平位移分布圖都不對稱，但支護兩側水平位移大小都一樣，只是方向相反而已。支護在外力的作用下由外側向內側產生變形，最大水平位移出現在支護兩側中部，最大值分別為2.27×10-4、2.86×10-4m。產生水平方向變形的主要原因是受到水平向圍巖壓力。

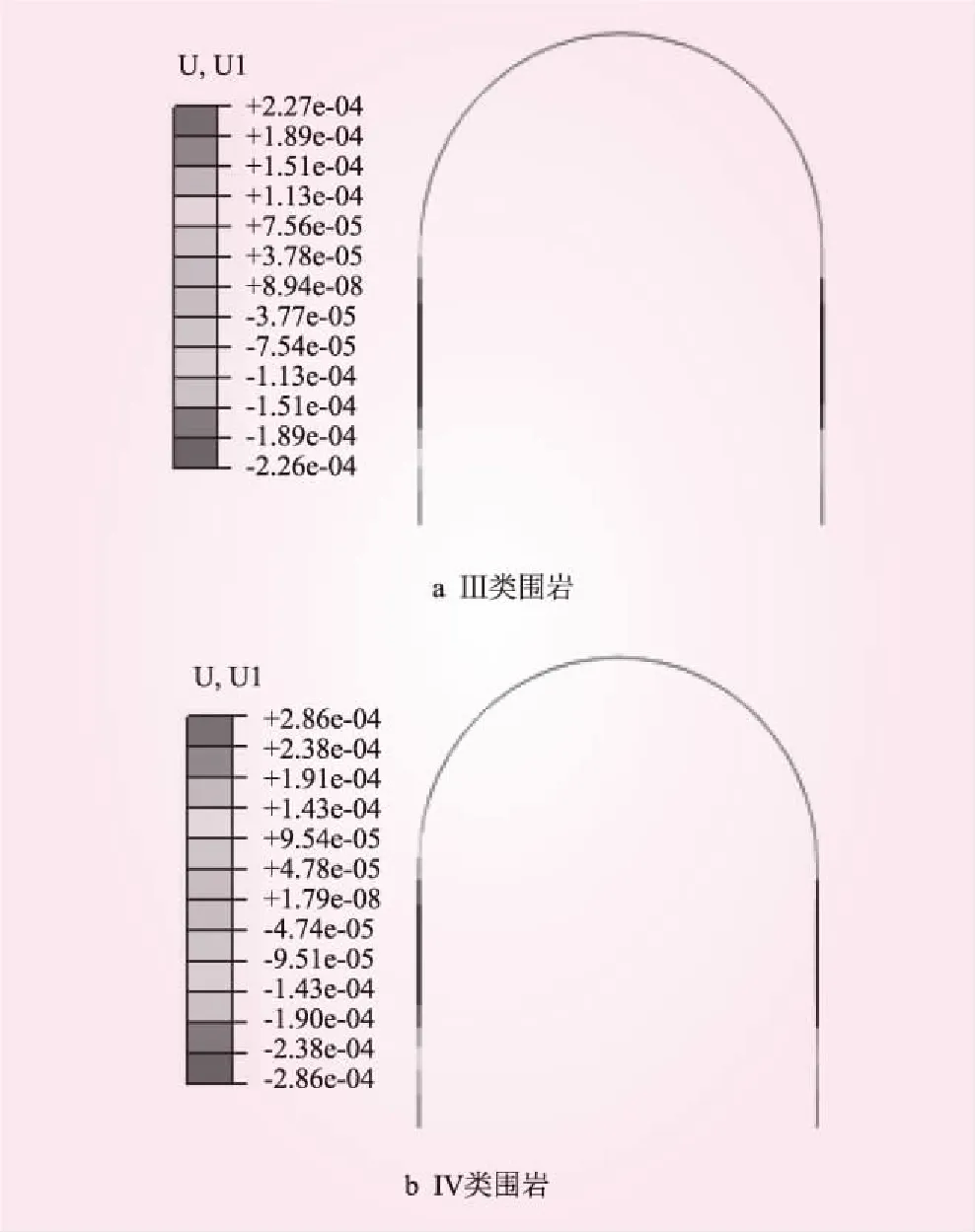
圖4 支護水平位移(單位：m)

Ⅲ類和IV類圍巖支護豎直位移見圖5。從圖5可知，Ⅲ類和IV類圍巖支護豎直位移分布圖都是左右對稱分布。最大豎直位移都出現在支護頂部，最大值分別為2.44×10-4、3.24×10-4m，方向向下。豎直向變形的主要原因是受到豎直向圍巖壓力和重力的共同作用。

由于水平方向荷載僅為圍巖壓力，水平方向變形相對于豎直方向較小。但總體來說，支護在水平方向和豎直方向變形量都很小，其主要原因是支護在圍巖與襯砌之間存在相互作用力，相互之間產生約束，從而使其變形受到了限制。

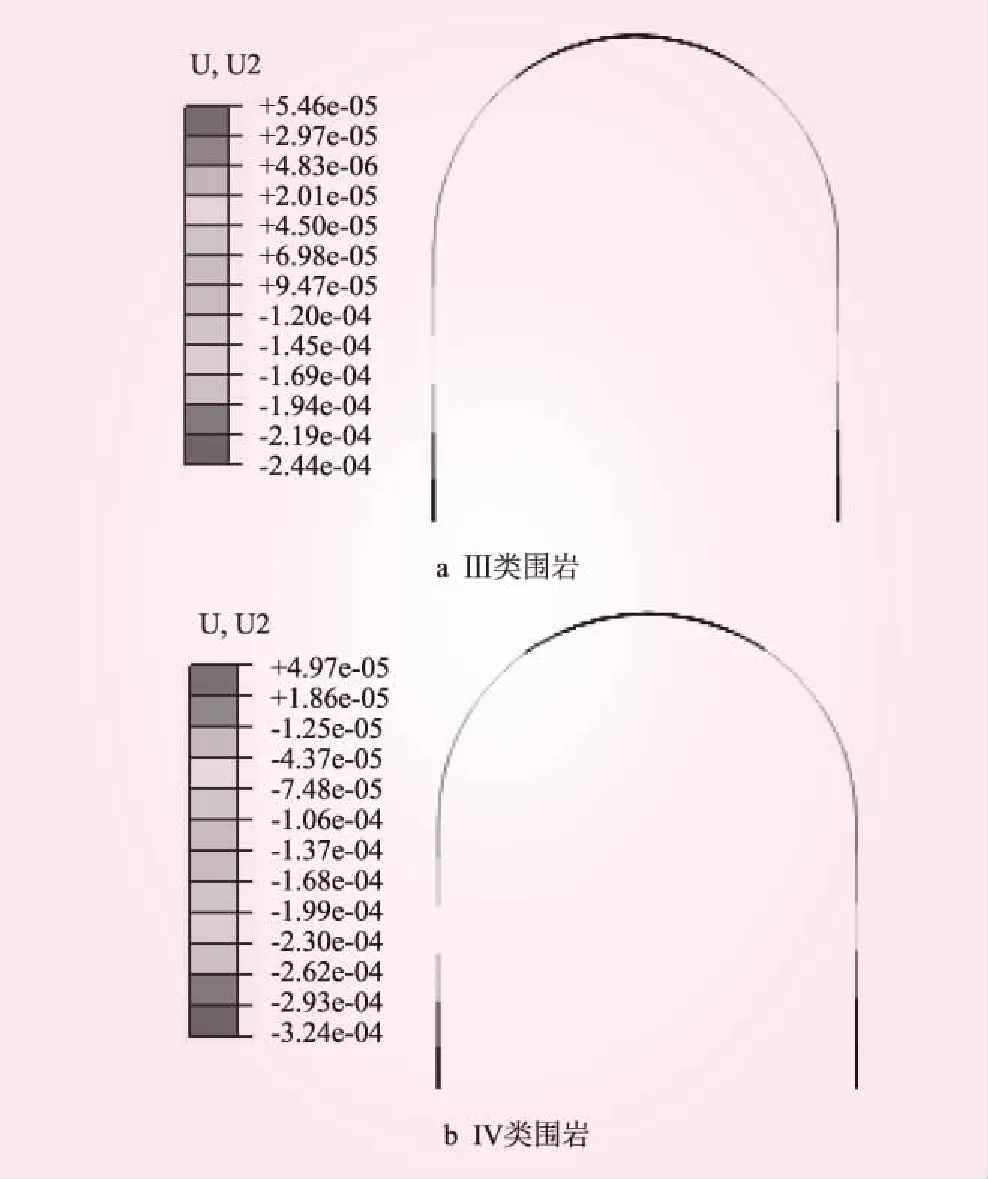
圖5 支護豎直位移(單位：m)

Ⅲ類和IV類圍巖支護軸力見圖6。從圖6可知，Ⅲ類和IV類圍巖支護軸力分布圖都是左右對稱分布，最大軸力出現在支護底部和中上部，分別為1.32×105、1.71×105N。在外部圍巖壓力和重力的共同作用下，整個支護結構都處于受壓狀態。

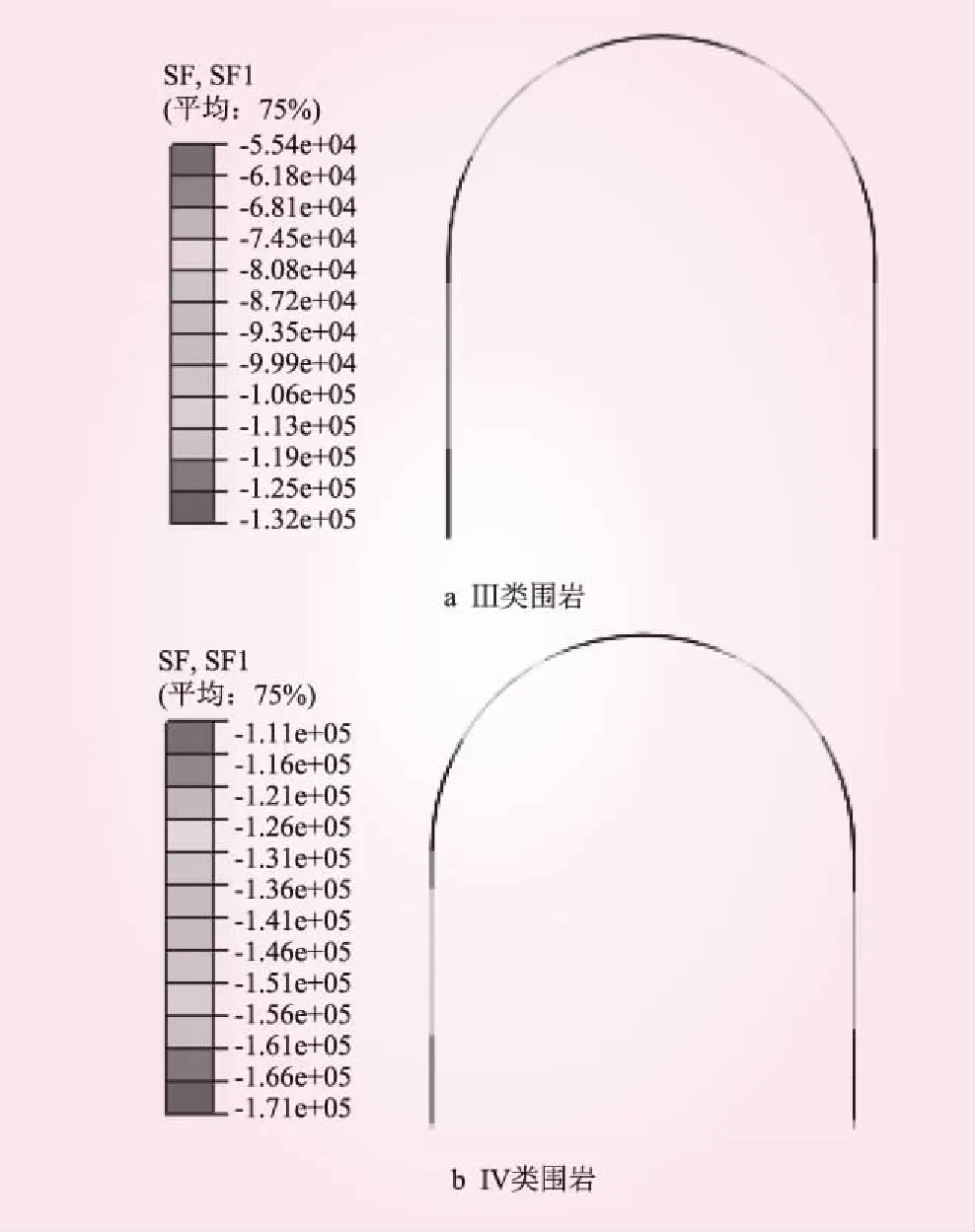
圖6 支護軸力(單位：N)

Ⅲ類和IV類圍巖支護彎矩見圖7。從圖7可知，Ⅲ類和IV類圍巖支護彎矩分布圖都是左右對稱分布，最大彎矩出現在支護底部，最大值分別為3.63×103、8.71×103N·m，所受彎矩方向既有向內也有向外。

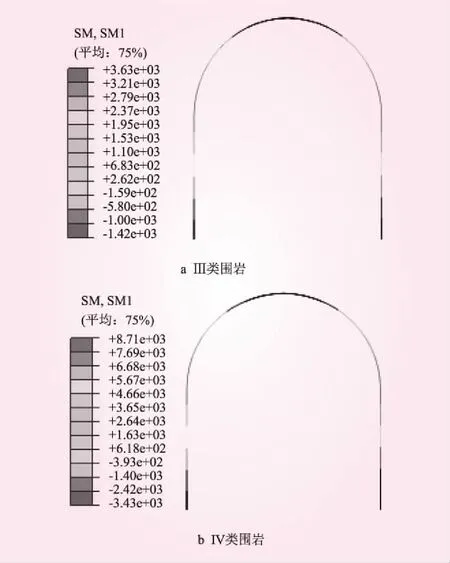
圖7 支護彎矩(單位：N·m)

3.3 錨桿內力

Ⅲ類和IV類圍巖錨桿軸力見圖8。從圖8可知，Ⅲ類和IV類圍巖整體錨桿軸力分布圖都是左右對稱分布，最大值都出現在錨桿底端，圖8a最下邊2根和圖8b最下邊4根錨桿底端軸力分別達到最大，最大值分別為3.52×104、4.2×104N。由于錨桿對支護拉力作用，整個錨桿處于受拉狀態，由外向內軸力逐漸增大。

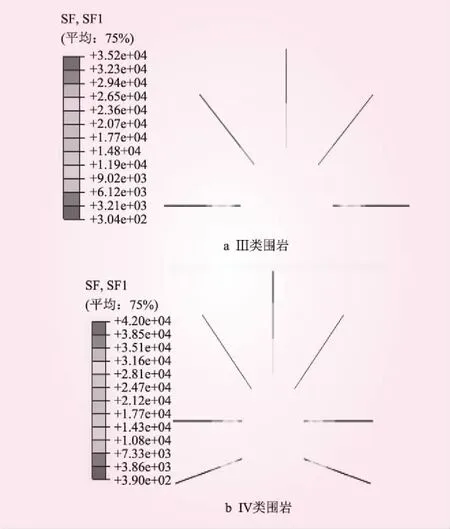
圖8 錨桿軸力分布(單位：N)

3.4 計算結果

Ⅲ類和IV類圍巖計算結果見表2。從表2可知：

表2 不同級別圍巖計算結果

(1)對于圍巖變形，隨著圍巖級別下降，最大等效位移增加了58.84%，但圍巖最大等效塑性應變減少了25.74%；對于支護變形，隨著圍巖級別下降，最大水平位移和最大豎直位移分別增加了25.99%、32.79%；對于支護內力，隨著圍巖級別下降，最大軸力和最大彎矩分別增加了29.55%、139.94%；對于錨桿內力，隨著圍巖級別下降，錨桿最大軸力增加了19.32%，增加率最小。

(2)雖然圍巖等級不同，但二維有限元計算得到的內力及變形分布規律相似，且大部分分布圖左右對稱。各內力區及變形區變化較小，最大值出現的位置幾乎沒有發生改變，可能與工程地質條件變化較小，圍巖級別相鄰，Ⅳ類圍巖比Ⅲ類圍巖多打了2根錨桿，使得Ⅳ類圍巖相應力學性能增加，變化趨勢不明顯等因素有關。可繼續增加圍巖種類，在圍巖打入錨桿數量一樣的情況下，得到更為系統的規律。由于洞室開挖造成巖體的臨空面易失穩，應力波動比較劇烈，導致軟弱、強度低的巖石破碎，破壞圍巖的整體性和連續性，使圍巖不能承受高的應力，不利于能量積累，容易出現應力降低帶。因此，隧洞工程要求圍巖等級不能太差。

4 結 語

本文基于地層結構法的三維有限元模型，利用了丁文其等提出的方法進行了地應力平衡，使得位移場基本為0，驗證了此種地應力平衡方法在斷面更大的隧洞中是可行的。與Ⅲ類圍巖相比，Ⅳ類圍巖除了圍巖最大等效塑性應變減少外，其他大部分內力及變形都會增加，尤其支護最大彎矩明顯增加，這個結果是Ⅳ類圍巖比Ⅲ圍巖多2根錨桿的前提下得出的，可見當錨桿數量取一樣時，增加得會更多。支護彎矩最大值出現的地方容易產生應力集中，可能會影響隧洞施工安全，所以在此區段應增加錨桿，以此來降低支護所承受的內力。