基于T-S型模糊加權的多模軟切換的風電機組變槳控制
侯濤,張強
(蘭州交通大學 自動化與電氣工程學院,甘肅 蘭州 730070)
風的間歇性和隨機性,增加了風電機組的控制難度,尤其是在額定風速以上,對于主動變槳型風力發電機組需要更加安全可靠的變槳控制策略。變槳系統作為變速恒頻風電機組的重要一部分,通常用在中、大型的風力發電系統中,其主要的控制目標是保持額定風速以上的功率恒定,限制風電機組的氣動轉矩和額外的功率吸收,減輕機組各部件的疲勞載荷[1-3]。目前變槳控制器廣泛使用的仍然是PI(D)控制器,此類控制器存在一些明顯的缺陷,如參數不能自動調整、參數依賴程度強、魯棒性低等[4-5]。國內、外專家學者在變槳控制中使用了一些更加先進的控制方法,如蜂群算法、滑模變結構、神經網絡等。蜂群算法取得了良好的魯棒性,但其穩定性差,當風電系統出現隨機干擾時,系統易出現不穩定[6];滑模變結構控制取得了良好的快速性和較強的魯棒性,但其存在高頻抖振問題,與神經網絡和模糊控制等相結合的改進算法設計變槳控制器,達到了一定的控制效果,也無法從根本消除這一問題[7-8];RBF神經網絡變槳控制器取得了較強的適應性,較好的魯棒性和動態性能,但其結構和參數確定較為復雜[9-10];這些控制方法較為復雜且難以硬件實現。模糊控制器擁有優良快速性與魯棒性,模糊自適應控制器可自動地在線調整參數,二者都是依據專家經驗設計而成,已相對成熟且已硬件實現;多模態控制比單一控制有更好的抗干擾性能;本文將以上兩種智能控制方式與傳統的PI控制相結合于多模態控制中,提出了基于T-S型模糊加權的多模軟切換變槳控制策略。將檢測到的發電機的轉速與其額定轉速進行比較,大偏差時利用模糊控制的快速性優勢迅速減小偏差、抑制偏差的快速變化;中等偏差時切換到模糊自適應PID控制,進行在線時時調整;小偏差時切換到PI控制,提高穩態精度。切換時根據發電機的轉速與其額定轉速的偏差大小及其變化率,利用T-S型模糊推理,使用加權平均法進行清晰化,輸出3種模態的權值,使用加權求和法合成輸出控制量。
1 風電系統數學模型
1.1 風速模型
風在流動的過程中具有很強的隨機性和突變性,為了準確描述風速的變化特性,本文采用風速的四分量模型[11-12],即將風速分解為基本風vb、陣風vg、漸變風vr和隨機風vn。其組合風vw可表示為
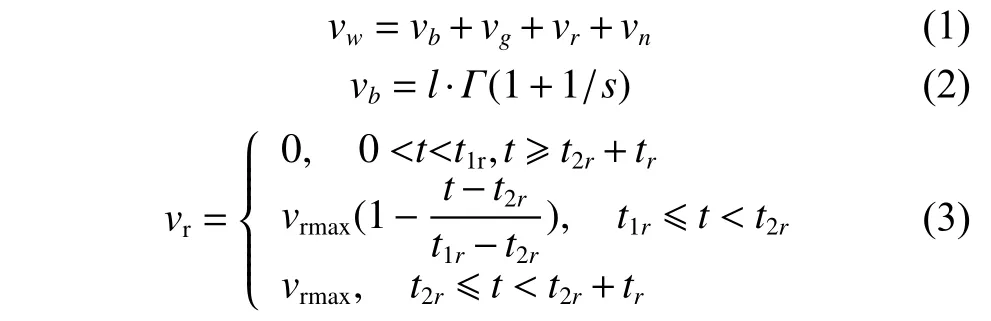
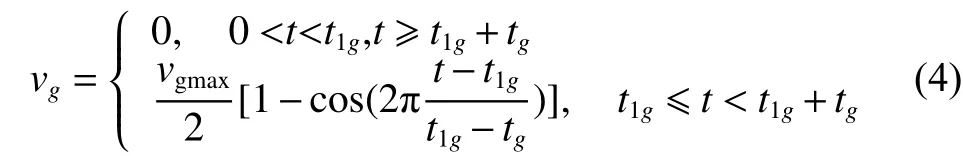

1.2 風力機數學模型
依據貝茲理論,風力機的數學模型[13-14]可表示為
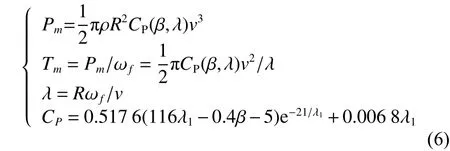
1.3 變槳執行機構數學模型
變槳的精度與靈敏度對功率有著很大的影響。其執行機構由伺服電機或液壓裝置驅動,可等效為一個一階慣性環節:
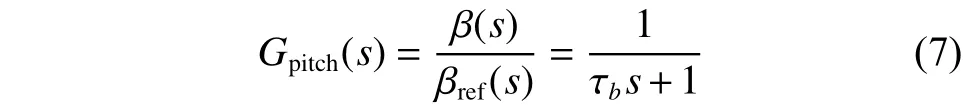
2 基于T-S型模糊加權的多模變槳控制策略
變槳控制是一種確保風電機組恒功率輸出的有效方法,減小額定風速以上風力發電機機組的過載,確保風電機組的最高效運行。通過控制槳距角限制風機的氣動轉矩,從而限制了額外功率的吸收,減輕了機組的疲勞載荷,使風電機組的機械功率保持恒定。在很多控制方案中,槳葉的轉速根據測量的風速實時修正,由于風在槳葉表面的每一點是不同的,故這種控制方案是不精確的。轉速與功率結合控制會造成轉速在最優運行點的輸出振蕩,降低了風電機組運行的可靠性[15-17]。本文通過測量發電機的轉速來對槳距角進行控制,限制風輪吸收的功率,以此來穩定機組的輸出功率。整體的控制框圖如圖1所示,ω為發電機的額定轉速,ω1為實測轉速。發電機的轉速與其額定轉速的偏差及其變化率經過T-S型模糊推理輸出3種控制模態的權值,將3種權值加權到對應的模態控制來實現多模軟切換,多模軟切換控制的控制策略就是在大偏差時利用模糊控制的快速性優勢迅速減小偏差、抑制偏差的快速變化,中等偏差時利用模糊自適應PID控制在線實時調整,在小偏差時切換為PI控制,提高控制的穩態精度。為了保證3種控制器之間的切換不會造成輸出量的振蕩,三者的切換采用基于T-S型模糊推理環節來實現,模糊推理采用加權平均法輸出各模態的權值,合成輸出采用加權求和法輸出控制量,確保3種控制之間的平滑過渡。合理的設置偏差的論域和模糊論域,能兼顧3種控制方法的優勢。
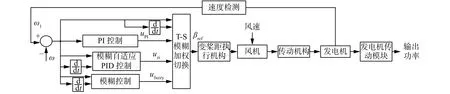
圖 1 T-S模糊加權變槳距控制框圖Fig. 1 Block diagram of T-S fuzzy weighted variable pitch control
2.1 模糊控制
模糊控制器采用二維模糊控制器。設發電機的轉速與其額定轉速的偏差為E,其變化率為EC。額定風速以上時,此時發電機的轉速高于額定轉速,偏差為正,采用單邊模糊控制。又知發電機的額定轉速為27.8 r/min=2.91 rad/s,E的基本論域為[0,8],EC 的基本論域為[–10,10],故設 E 的模糊論域為[0,4],EC的模糊論域為[–6,6]。工程應用中要求槳距角在0°~25°之間變化,且不考慮負值,設控制量U的基本論域為[0,30],其模糊論域為[0,5]。E、EC和U的隸屬函數類型均取為三角型,分別如圖2~4所示。設E的模糊子集,E C模糊子集,輸出的模糊子集。的模糊控制規則表如表1所示。
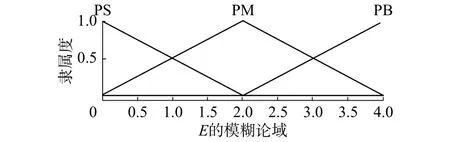
圖 2 E的隸屬函數Fig. 2 The membership of E
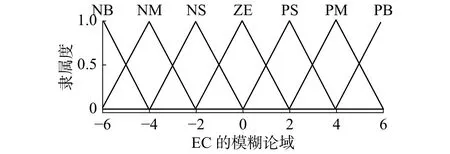
圖 3 EC的隸屬函數Fig. 3 The membership of EC
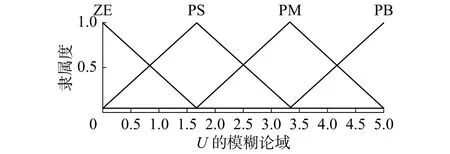
圖 4 U的隸屬函數Fig. 4 The membership of U
表 1 的模糊控制規則Table 1 The fuzzy control rule of
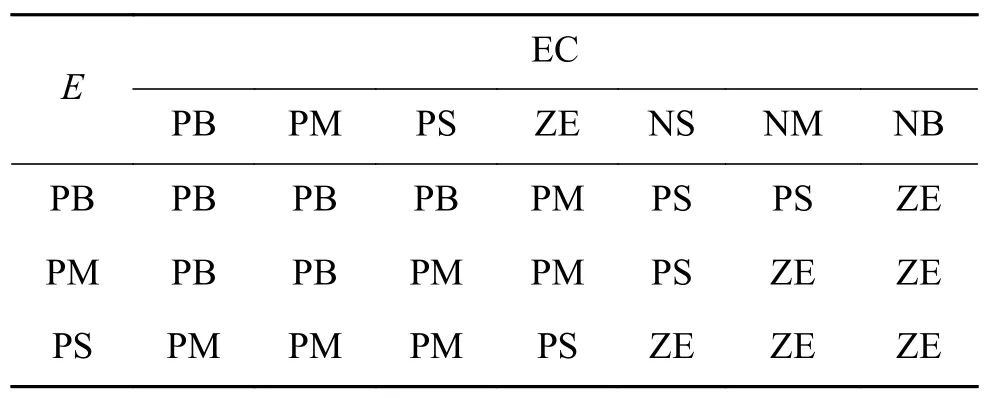
表 1 的模糊控制規則Table 1 The fuzzy control rule of
E EC PB PM PS ZE NS NM NB PB PB PB PB PM PS PS ZE PM PB PB PM PM PS ZE ZE PS PM PM PM PS ZE ZE ZE
2.2 模糊自適應PID控制
發電機的轉速與其額定轉速的偏差E及其變化率EC作為模糊自適應PID控制器的兩個輸入,利用模糊規則在線實時地調整PID的3個參數,實現對ΔkP、ΔkI、ΔkD參數的自整定。E和EC的基本論域與模糊論域同模糊控制的設置一樣。ΔkP、ΔkI、ΔkD的模糊論域分別設置為[–6,6],[–3,3],[–6,6],設 E 的模糊子集{PB,PM,PS},EC 模糊子集為{NB,NM,NS,ZE,PS,PM,PB},ΔkP、ΔkI、ΔkD的模糊子集分別設置為{NM,NS,ZE,PS,PM,PB},{NM,NS,ZE,PS,PM,PB},{NB,NM,NS,ZE,PS,PM,PB},E、EC、ΔkP、ΔkI、ΔkD的隸屬函數均為三角型,ΔkP、ΔkI、ΔkD的模糊控制規則表,如表 2~4 所示。
表 2 的模糊控制規則Table 2 Fuzzy control rule of
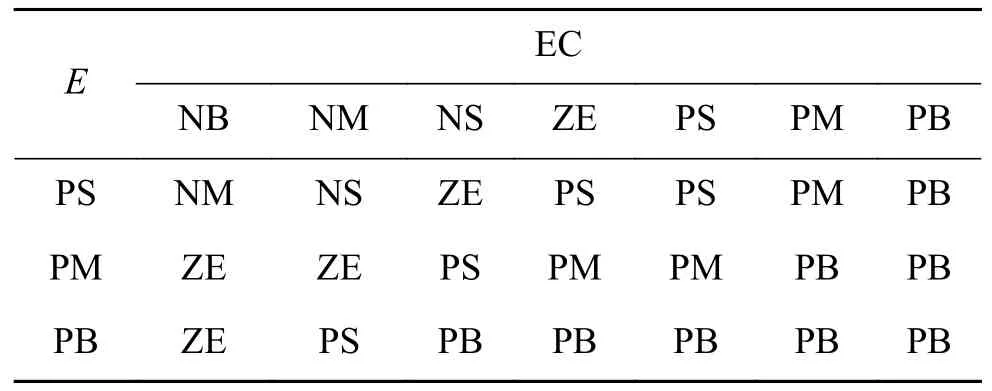
表 2 的模糊控制規則Table 2 Fuzzy control rule of
EC NB NM NS ZE PS PM PB PS NM NS ZE PS PS PM PB PM ZE ZE PS PM PM PB PB PB ZE PS PB PB PB PB PB E
表 3 的模糊控制規則Table 3 Fuzzy control rule of
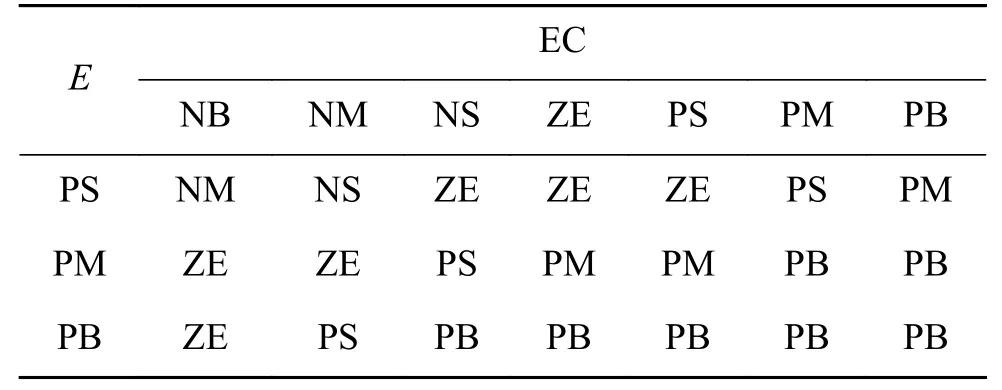
表 3 的模糊控制規則Table 3 Fuzzy control rule of
EC NB NM NS ZE PS PM PB PS NM NS ZE ZE ZE PS PM PM ZE ZE PS PM PM PB PB PB ZE PS PB PB PB PB PB E
表 4 的 模糊控制規則Table 4 Fuzzy control rule of
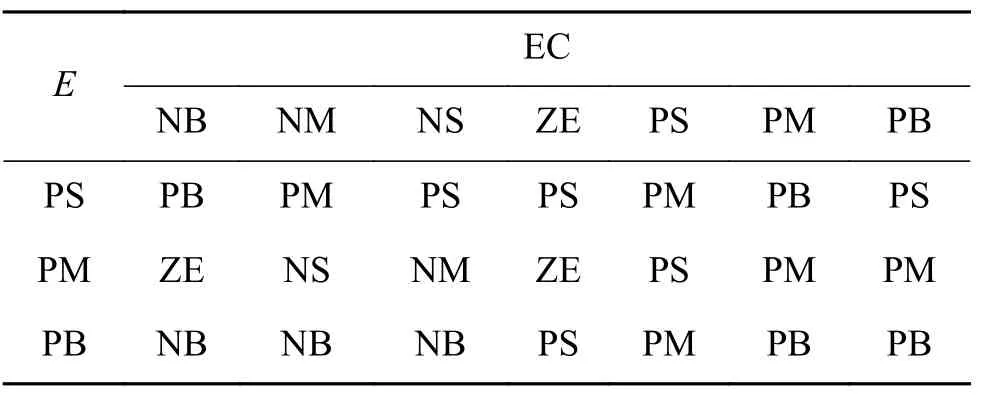
表 4 的 模糊控制規則Table 4 Fuzzy control rule of
EC NB NM NS ZE PS PM PB PS PB PM PS PS PM PB PS PM ZE NS NM ZE PS PM PM PB NB NB NB PS PM PB PB E
2.3 PI控制
PI控制是PID控制的一種特例,當系統的偏差較小時,采用PI控制可以使控制系統具有較好的穩態性能。
3 基于T-S型模糊加權的多模軟切換設計
3.1 設計原理
T-S型是一種適于表達復雜系統的動態特性,其輸出的隸屬函數可以是線性的或者是單點常數[18]。本文主要利用T-S型模糊推理的隸屬函數為單點常數使得其輸出為單點常數這一特點來實現軟過渡。區別于傳統的切換方法只在某一閾值進行切換,本文引入了偏差及其導數,在到達閾值的前幾個時刻,此時偏差小于設定的閾值,若偏差的變化率較大,本文使用的方法就進行了模態切換;同樣,在到達偏差的后幾個時刻,此時偏差大于設定的閾值,若偏差的變化率較小,本文使用的方法就不進行模態切換;具體的切換時刻由T-S型模糊推理實現,這也充分利用了模糊控制智能化的優勢。T-S型模糊加權多模切換設計的目的是利用T-S型模糊推理平滑多種控制模態的輸出,T-S型模糊加權切換的輸出為模態的權值。其基本思想是根據系統的轉速誤差信息,需要在3個模態之間進行切換時,引入轉速偏差和其導數進行模態切換判斷,應用T-S型模糊推理方法,清晰化采用加權平均法,得到切換過程中3個模態的權值,使用加權求和法將3個模態的權值加權到3個模態的輸出,從而平滑控制器的輸出,實現T-S型模糊加權多模軟切換。
3.2 模糊化
T-S型模糊加權算法的模態劃分取決于發電機的轉速與其額定轉速的偏差E及其變化率EC,利用這兩個量來確定T-S型模糊推理各模態的權值。由于風速處于額定風速以上,此時轉速高于額定轉速,偏差為正,故采用單邊模糊控制。選取發電機的轉速與其額定轉速的偏差E和偏差變化率EC的論域和模糊論域同前文模糊控制一樣,E的模糊子集為,EC的模糊子集為。
3.3 模糊推理
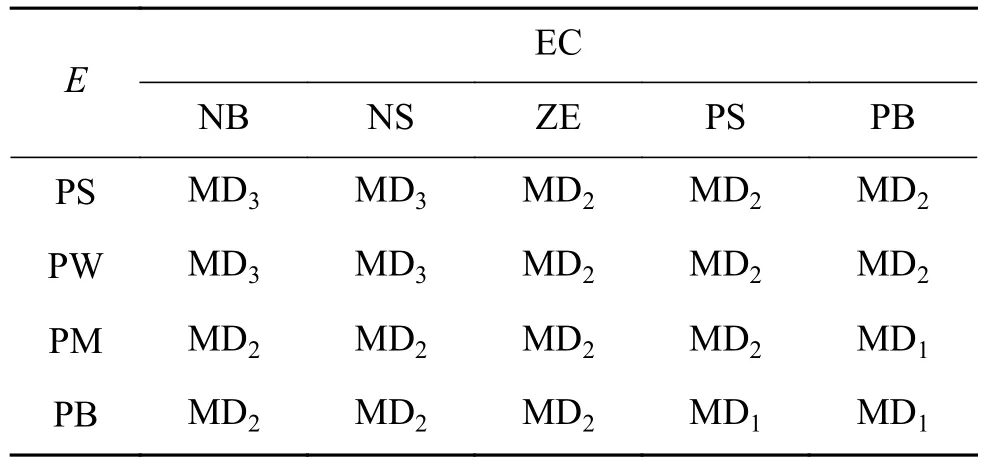
表 5 模態模糊規則描述Table 5 The description of modal fuzzy rule
3.4 去模糊化
T-S型模糊控制的去模糊化采用加權平均法,設第 i 條規則輸出的結果為,它的權重為,為規則數,則總輸出為
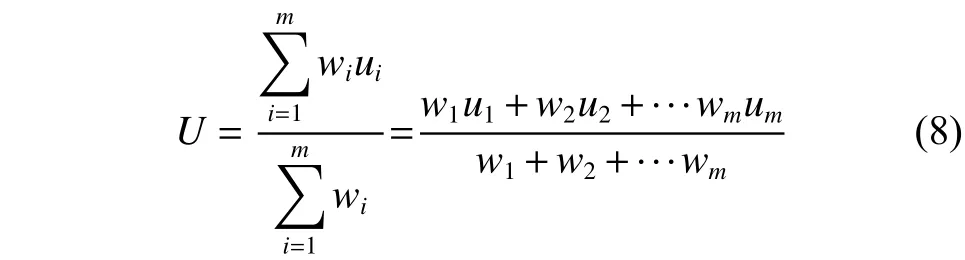
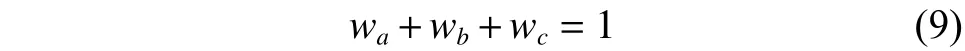
3.5 T-S型模糊切換合成輸出
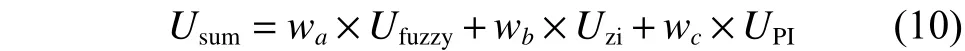
4 仿真分析與驗證
為了驗證所提方法的正確性及其控制性能,在SIMULINK下搭建了直驅永磁同步發電系統在單獨模糊控制、單獨模糊自適應PID控制、單獨PI控制以及基于T-S型模糊加權的多模軟切換控制的4種變槳控制模型,以階躍風速和組合風速分別作為系統的輸入,并將4種控制方法的仿真結果進行對比。風機的額定風速為,等效的轉動慣量為54 894 kg·m2,葉片半徑R為46.74 m,空氣密度為,發電機的額定功率P為2 MW,定子電阻為0.006 65 Ω,定子電感L為0.002 4 H,永磁體的磁鏈為1.67 Wb,極對數為60,轉動慣量為411 185。對于模糊控制,E、EC、U對應的量化因子分別為、、;對于模糊自適應PID控制,取其初始參數為,,;對于PI控制,取,。
利用SIMULINK中的模糊控制工具箱建立T-S型的模糊推理系統如圖5所示。
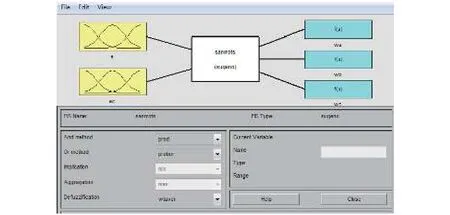
圖 5 T-S型模糊推理系統Fig. 5 The T-S fuzzy inference system
經過模糊規則設定,得到其輸出權值在ruler viewer如圖6所示。
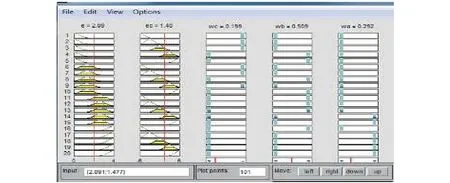
圖 6 ruler viewer中的權值輸出Fig. 6 The weight outputs in ruler viewer
由圖6可知,其權值輸出滿足式(9)。此時為中等偏差,偏差的變化率也中等,故模糊自適應PID控制的權值較大,模糊控制和PI控制的權值較小。
1) 階躍風速
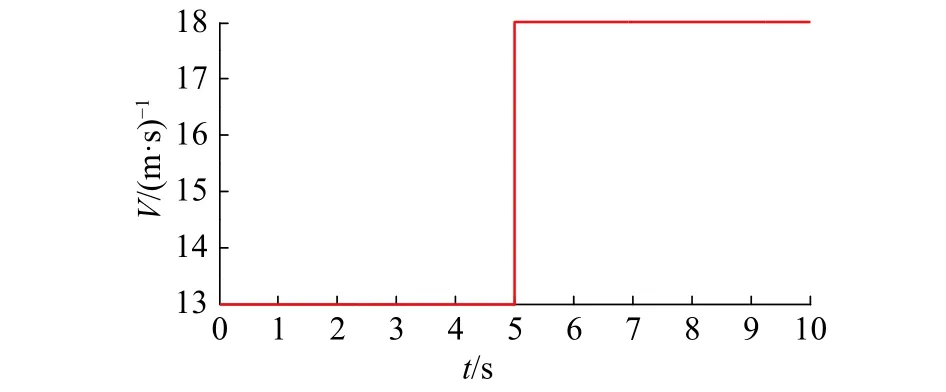
圖 7 風速Fig. 7 The curve of wind speed
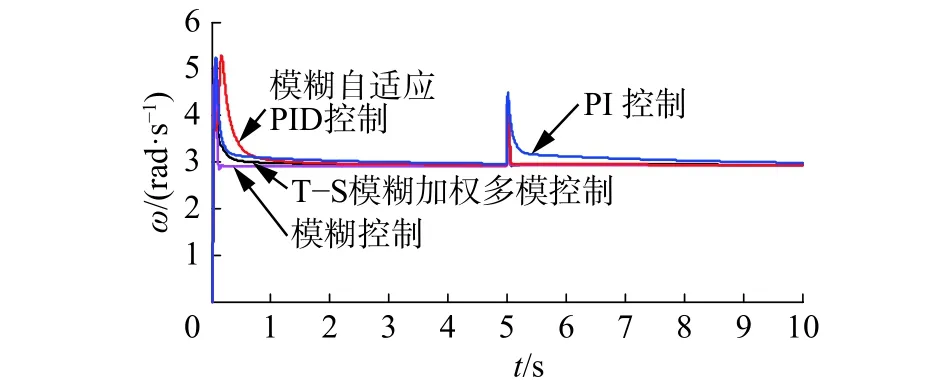
圖 8 轉速對比Fig. 8 The comparison of rotor speed
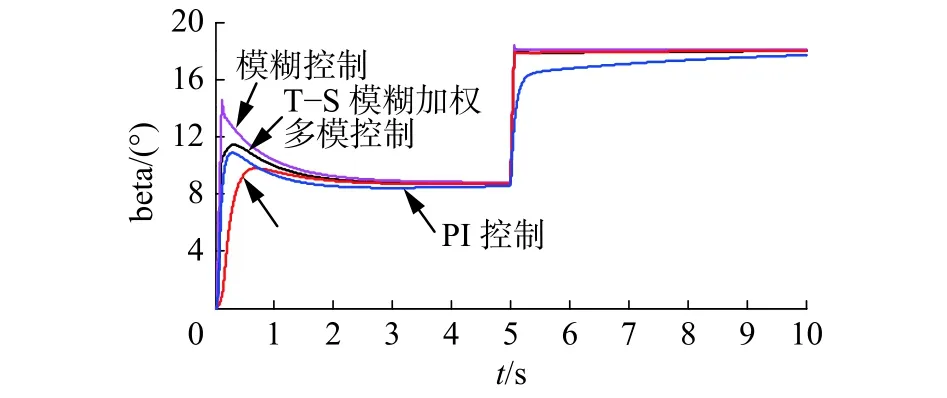
圖 9 槳距角對比圖Fig. 9 The comparison of pitch angle
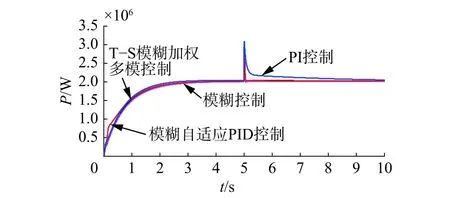
圖 10 輸出功率對比Fig. 10 The comparison of generator output power
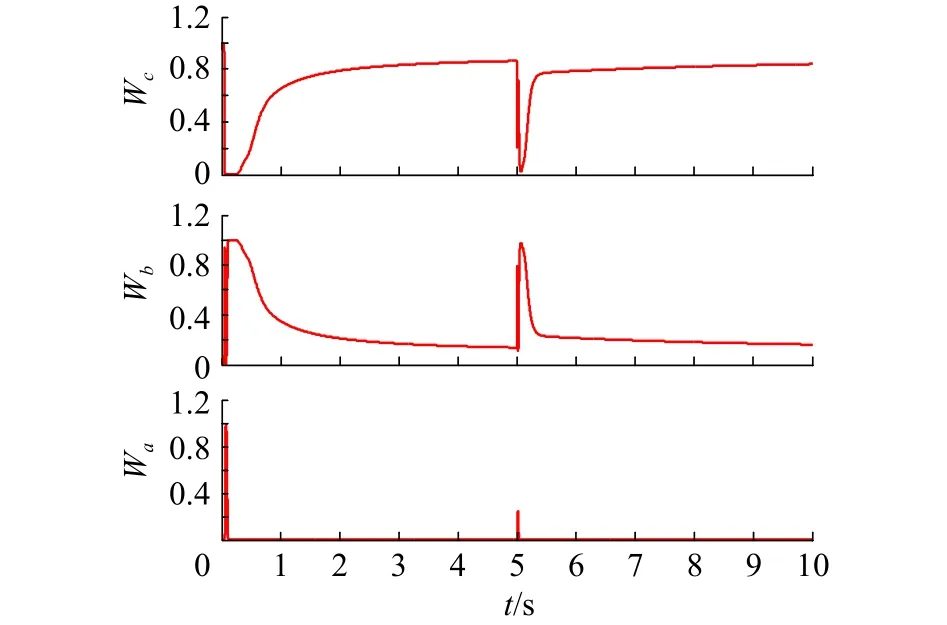
圖 11 T-S型模糊推理的權值輸出Fig. 11 The weight output of T-S fuzzy inference
2)組合風速
采用組合風速模型時,vn用式(11)代替:
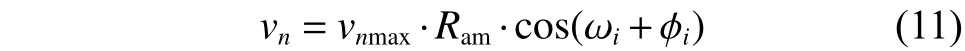
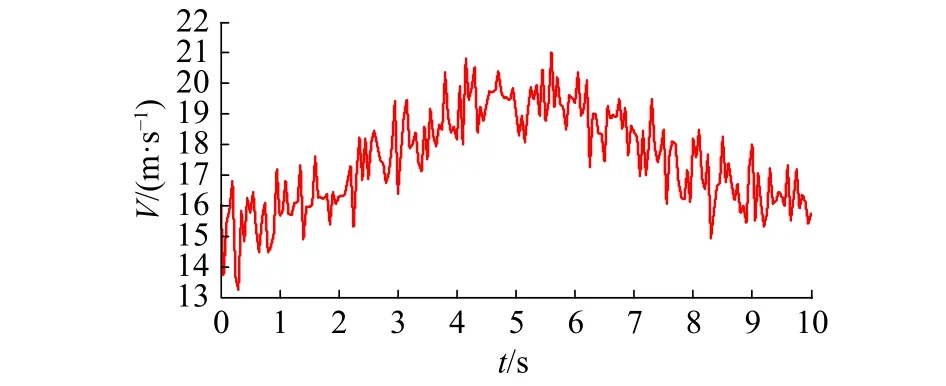
圖 12 風速Fig. 12 The curve of wind speed
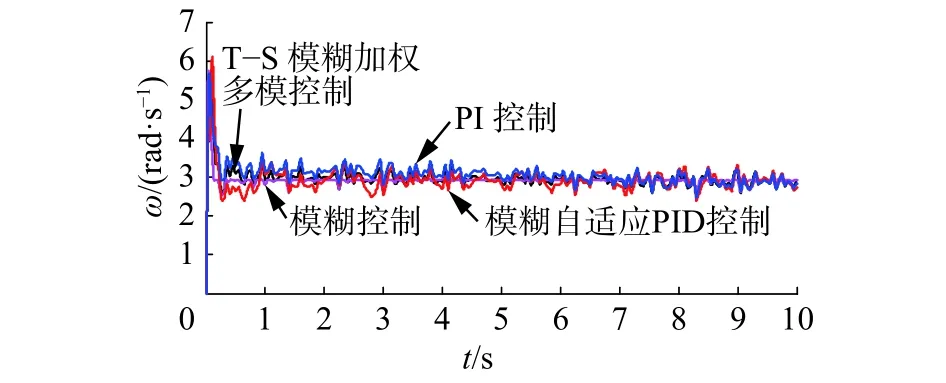
圖 13 轉速對比Fig. 13 The comparison of rotor speed
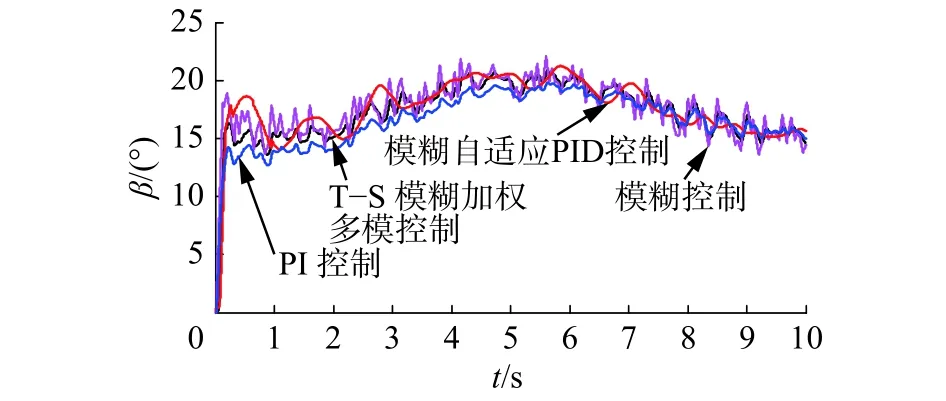
圖 14 槳距角對比Fig. 14 The comparison of pitch angle
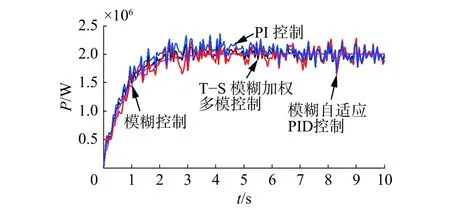
圖 15 輸出功率對比Fig. 15 The comparison of generator output power
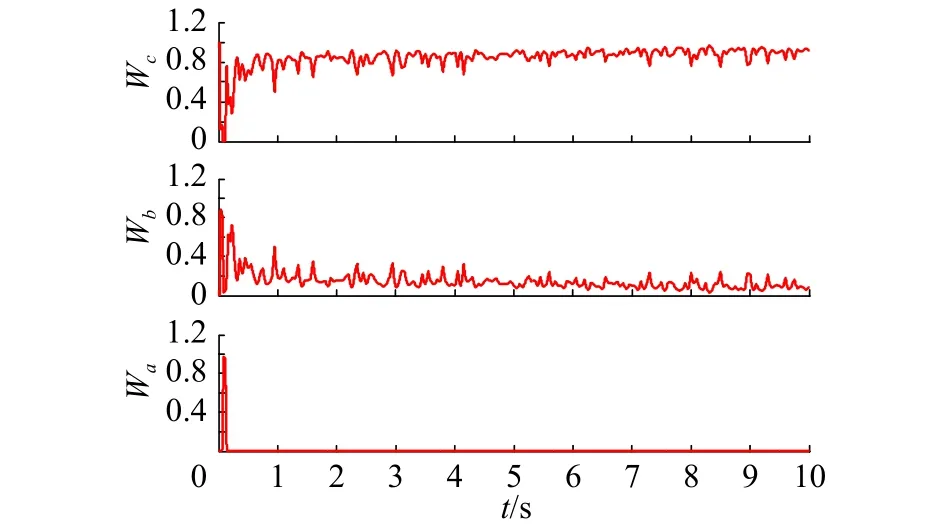
圖 16 T-S模糊推理的權值輸出Fig. 16 The weight output of T-S fuzzy inference
仿真結果表明:階躍風速和組合風速下,4種控制方法都能使發電機的輸出功率穩定在額定值附近。使用模糊控制時,輸出的功率與轉速波動更小,更加平穩,但當風速改變時,其槳距角響應過于迅速,超調量大且波動較大,導致槳距角執行機構的頻繁動作,增加了槳距角執行機構及風電機組各部件的機械疲勞載荷。所提出方法的綜合控制性能優于其他3種方法,通過改變槳距角可以使轉速較快地趨于穩定,即可以快速跟蹤發電機的額定轉速,功率也能穩定在發電機輸出的額定功率附近。與其他3種方法相比,調節槳距角更加地平滑、動作頻率更低,幅度更小;與模糊自適應PID與PI控制相比,減小了轉速的峰值,轉速與功率的脈動更小。階躍風速下,進入穩態后,在5 s突加擾動時,又表現出良好的抗干擾性能。
5 結束語
本文針對現有的變槳控制策略存在風電機阻額定風速以上恒功率運行時,槳距角執行機構的頻繁動作增加了風機各部分的機械疲勞載荷,影響發電機的輸出電能質量和機組的使用壽命等問題,研究了基于T-S型模糊加權的多模軟切換變槳控制方法。該方法兼顧了模糊控制、模糊自適應PID控制和PI控制各自的控制優勢,并利用TS型模糊推理來進行平滑過渡,實現了軟切換,克服了切換振蕩。仿真結果表明,所提出的方法具有更加優良的綜合控制性能,具有良好的動態性能、穩態性能和魯棒性。在兩種風速下,調節槳距角更加平滑,減緩了執行機構的頻繁動作,槳距角執行機構的疲勞載荷有效的減小了,從而降低了機組其他部分的機械載荷,延長了機組的使用壽命。從對比研究易知,4種方法都能跟蹤上發電機的轉速并維持在額定轉速,都能使發電機的輸出功率穩定在額定值(2MW)附近,但所提出的方法轉速的峰值更低,脈動更小,功率更加靠近額定值,功率脈動更小,更平穩。對于輸出功率的脈動,風電機組在并網時加入背靠背變頻器可以解決這一問題。此方法對于直驅變槳永磁同步風力發電系統,在額定風速以上的恒功率運行有一定的借鑒參考價值。

