水位上升對土坡穩定性的影響

柴學銳，孫冬梅，S. Semprich

(1.天津大學 水利工程仿真與安全國家重點實驗室，天津 300072；2.格拉茨技術大學 土力學及基礎工程研究所，奧地利 格拉茨 A-8010)

坡外部水位升高，岸坡土體內的地下水位也隨之發生改變，原來被氣占據的孔隙空間逐漸被水所補充，在這種“水驅替氣”的過程中，孔隙壓力的變化將影響岸坡的穩定性。因此，研究水位上升作用下岸坡的滲流場變化情況對進一步研究岸坡穩定性變化規律至關重要[1-2]。

水位上升作用下的岸坡是一種常見的飽和-非飽和土坡。在以往的飽和-非飽和滲流問題中，一般僅研究水相而忽略氣相流動，盡管這種僅考慮水相的方法簡單易行并且已經積累了一定經驗，但得出的結論與實際工況相比有很大出入。因此，為了更好地模擬非飽和區流體的運移規律，國內外有學者認為采用水-氣二相流模型分析飽和-非飽和滲流問題更符合實際[3-7]。

基于水-氣二相流模型，分析了水位上升過程中，飽和-非飽和土坡內滲流場的變化規律；采用Bishop簡化法[8]推導出同時考慮孔隙氣壓力、毛細壓力和坡外水壓力等貢獻的土坡安全系數計算公式，并計算了不同時刻邊坡的安全系數；分析安全系數的變化規律及各個力對安全系數的貢獻，為進一步研究水位上升作用下土坡的失穩機理提供理論依據。

1 水-氣二相流模型

近年來，多孔介質的多相流理論研究和應用越來越受到學者重視[9]。對于巖土工程滲流問題而言，通常認為滲流系統絕對恒溫，土體骨架不變形，處于平衡狀態的水相(l)和氣相(g)在多孔介質中流動，且滿足Darcy定律。

1.1 基本控制方程

當非飽和土體中流體的擴散作用忽略不計時，飽和-非飽和水-氣二相流模型的基本控制方程為

(1)

1.2 本構方程

1.2.1 毛細壓力-飽和度關系模型

近年來，許多學者均提出了毛細壓力和飽和度的關系模型，如Brooks and Corey(BC)模型[10]和Van Genuchten(VG)模型[11]等，其中BC模型的進氣值不具備連續性，而Van Genuchten(VG)模型不僅其表達形式簡單，且模型的關系曲線中進氣值和殘余水飽和度處過度平滑，因此在水-氣二相流模型中Van Genuchten(VG)模型得到廣泛應用

(2)

式中：pc為水相和氣相交界面處的毛細壓力，等于孔隙水壓力和孔隙氣壓力的差值；P0為進氣值；參數Sle為有效水飽和度，Sle=(Sl-Slr)/(Sls-Slr)，其中Sl為水飽和度，Slr為殘余水飽和度，Sls為飽和水飽和度；λ、ζ為模型的擬合參數，其值與土壤自身性質有關；Pmax為最大毛細壓力。

1.2.2 相對滲透率和飽和度關系

土體孔隙中同時存在氣相流體和水相流體，一種流體流動將會干擾另一種流體的流動，當水飽和度變化時，水相和氣相之間的交界面也將隨之變化，水流通道的彎曲度將會改變，導致相對滲透率發生改變。1976年，Mualem提出了相對滲透率和飽和度的關系表達式，將反應毛細壓力和飽和度關系的VG模型表達式帶入相對滲透率和飽和度的關系表達式中，可得到TOUGH2中相對滲透率和飽和度關系的改進模型，即VGM模型[12]

(3)

式中：krl為水相相對滲透率；krg為氣相相對滲透率；τ為迂曲因子，其取值大小與土體孔隙彎曲度有關，這里取0.5。

1.3 邊界條件處理方法

邊界條件實際上是指研究區域邊界所處的條件。在數學模型中，通過在滲流場邊界施加一薄層虛擬單元來實現各種邊界條件的數值模擬。其中，第一類邊界條件(Dirichlet條件)和第二類邊界條件(Neumann條件)為水-氣二相流模型根據液相和氣相劃分的邊界條件。

1.3.1 第一類邊界條件

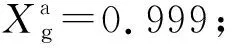
1.3.2 第二類邊界條件

第二類邊界條件主要用來描述系統與外界的流量交換情況，且第二類條件可以是常量，也可以是隨時間變化的量。將上升引起的加載作用等效為邊界單元上有一個流入的流量，該值可通過式(4)求解

(4)

式中：m為源匯項，流入為正；b為擬合系數，擬合系數的取值與土壤的性質有關；V為邊界單元的體積；C為邊界單元的壓縮性；ΔP為水壓力的變化量；Δt為水壓力變化所需的時間。以往的研究通常將水位變化過程等效為一系列特征水位，這種處理方法不能很好地模擬邊界上相態的轉變，而將水位上升過程等效為邊界單元上有一個流入的流量，可以實現水位的連續變化和邊界上相態的轉變。

1.4 初始條件

初始條件即為t=0時刻土體中各個狀態變量的分布情況。求解土體穩定滲流問題時，只需給出相應的邊界條件即可，不需給定初始條件，但是求解土體非穩定滲流問題時，除了給出邊界條件之外，還需給定初始條件。對于坡外水位上升作用下的非穩定滲流問題，迭代求解的時間取決于給定的初始條件的合理性，當初始條件接近真實值時，迭代收斂速度會加快，所需要的模擬時間會減少，因此初始條件的給出應該以接近實際物理意義為準則。

2 非飽和土坡穩定性分析方法

2.1 非飽和土坡抗剪強度公式

Fredlund等[13]認為非飽和土的抗剪強度由凈法向應力、基質吸力和有效黏聚力組成，由此提出了非飽和土的抗剪強度公式

τ=c′+(σn-pg)tanΦ′+(pg-pw)tanΦb

(5)

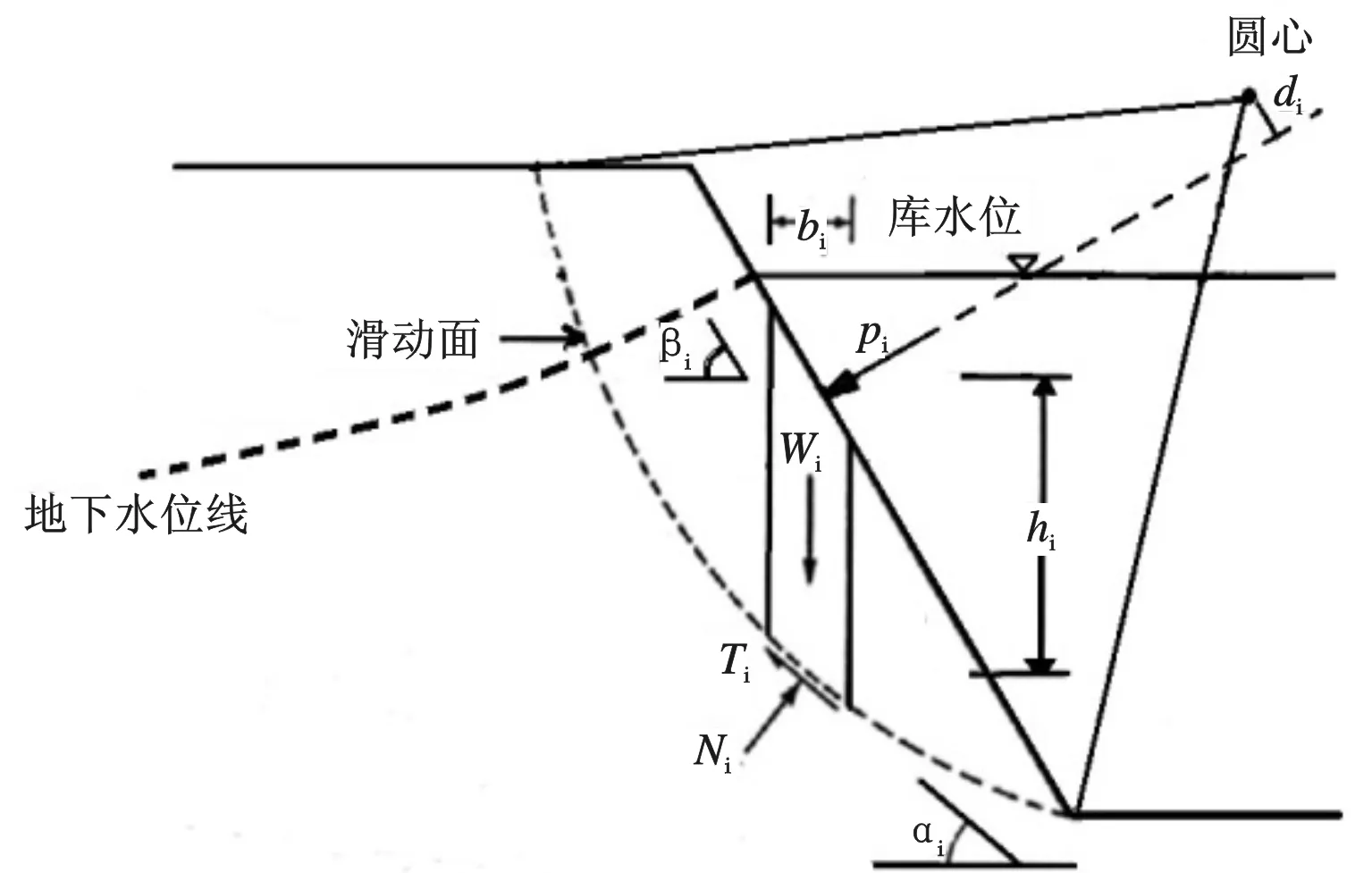
圖1 Bishop簡化法下的土條作用力Fig.1 Forces acting on a slice in simplified Bishop′s Method

式中：τ為非飽和土的抗剪強度；c′為有效黏聚力；σn為總法向應力；pg=pg-patm為孔隙氣壓力；pw=pw-patm為孔隙水壓力；Φ′表示有效內摩擦角；Φb表示抗剪強度隨基質吸力增加的曲線傾角；(σn-pg)為凈法向應力；(pg-pw)為基質吸力，其值等于負的毛細壓力[14]。

2.2 非飽和土坡安全系數計算公式

Bishop簡化法常用來計算某一危險圓弧滑動面上的安全系數。圖1為一均質非飽和土坡，土坡中任一土條i上的作用力如圖所示：bi為土條i的寬度；αi為土條i的底面與水平方向的夾角；βi為土坡側面與水平方向的夾角；Wi為土條i的重力；Ni為土條i底部的正法向應力；Ti為土條i底部的切向力；hi為土條i的高度；pi為作用在土條i上的坡外水壓力。

根據土條i在垂直方向上受力平衡

(6)

根據圓心力矩平衡

(7)

式中：di為坡外水壓力pi到圓心的垂直距離，R為半徑。

根據極限平衡條件，土條i底面的抗剪力Ti可表示為

(8)

則非飽和土坡圓弧滑動面上的安全系數F可表示為

(9)

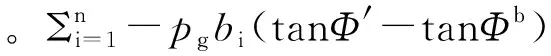
3 算例分析

3.1 算例說明

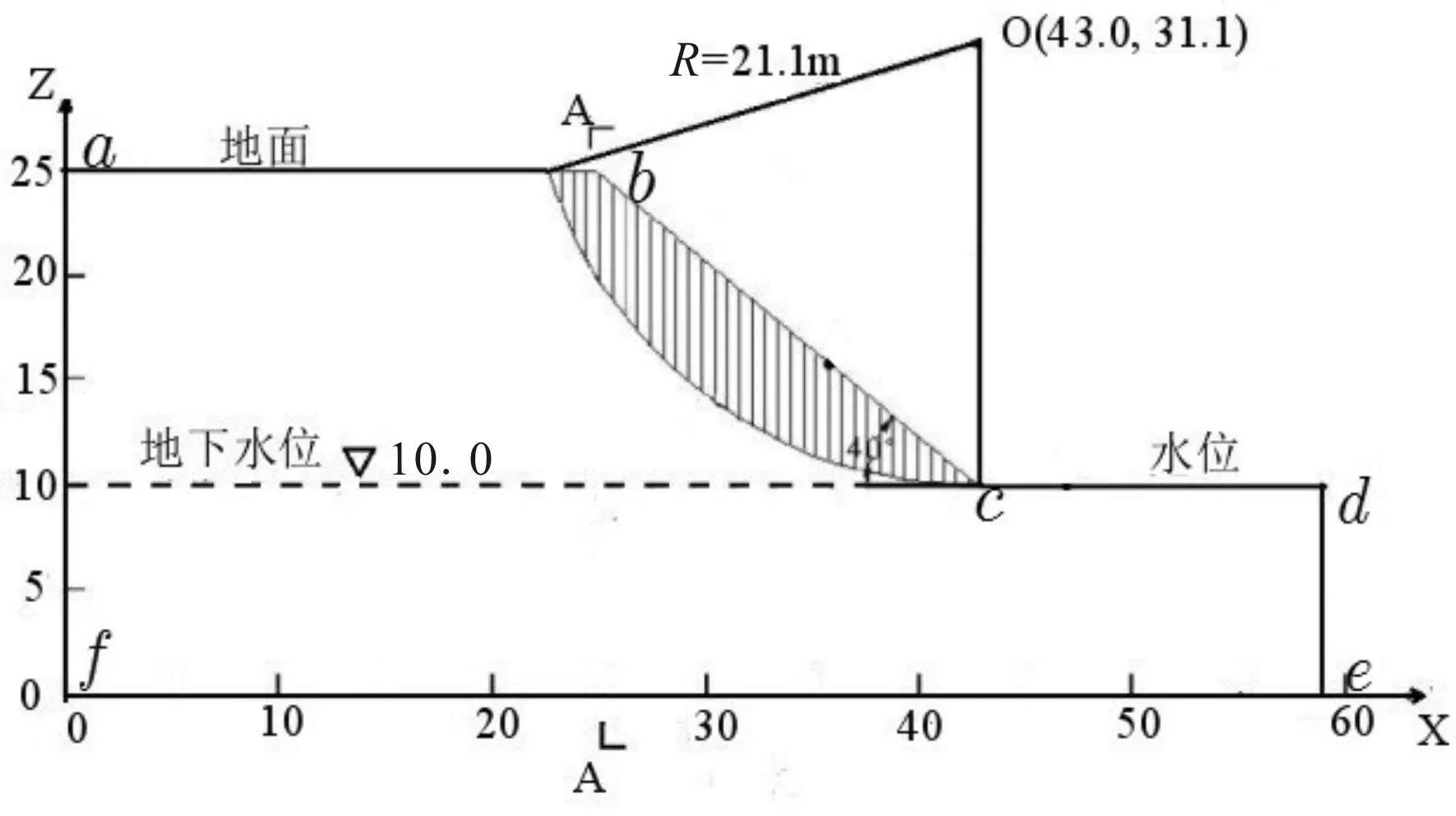
圖2 邊坡幾何形狀剖面圖(單位：m)Fig.2 Cross section of soil slope

圖2為一個各向同性的勻質土坡，該土坡長58.0 m，寬30.0 m，左側坡高25.0 m，右側坡高10.0 m，坡面傾角40°，坡內坡外的水位水平，且水位高程均為10.0 m。為了保證模擬結果的精確程度，對土坡進行網格剖分，若網格尺寸剖分過小，則計算時間較長且計算結果精度并未有明顯提升，若網格尺寸剖分過大，將導致模擬結果精確程度降低，因此，根據筆者已有經驗將網格剖分成水平方向上從0.5 m到1.0 m不等，垂直方向的網格尺寸均為0.5 m。在土體處于完全飽和的狀態下，采用Bishop簡化方法計算得到最危險圓弧滑動面的圓心坐標為(43.0，31.1)，半徑為21.1 m，且其中一條半徑與水平方向垂直。在該土坡上設置一個追蹤面A-A，該追蹤面處于土坡的中間偏左位置，其水平坐標是25.0 m。

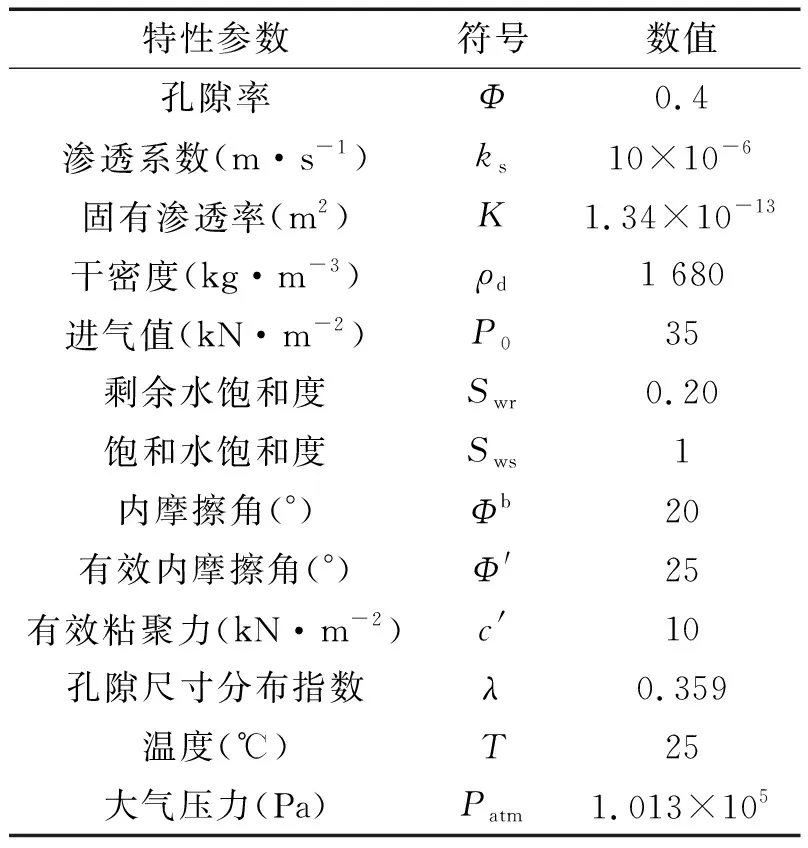
表1 土體特性參數Tab.1 Parameters of different soils

整個模擬過程中，設定研究區處于恒溫系統中，表1給出土體的特性參數取值。

3.2 滲流場分析

初始穩態的邊界條件包括地表(如圖2中ab邊所示)和坡外水位以上的右側邊界(如圖2中bc邊所示)為大氣邊界，坡外水位以下(如圖2中cd和de邊所示)為水相邊界，區域左側(如圖2中af邊所示)和底部(如圖2中ef邊所示)為不透水邊界，在此邊界條件下，運行模型直至毛細壓力與重力平衡。水位上升過程中，坡外水位在52 h內從10.0 m快速上升至21.2 m，上升速度為0.598×10-4m/s，該過程中，地表面和坡外水位以上的右側邊界仍為大氣邊界，區域左側和底部仍為不透水邊界，但原來在水位以上的右側氣相邊界隨著水位上升逐漸被水淹沒，轉變為水相邊界。

模擬過程中，在邊界單元上施加源匯項，以實現由于水位上升引起的加載作用導致的邊界單元上的水壓力變化和相態的轉變。初始的源匯項值可以通過式(4)計算得到，經過試算，得出水位上升過程的源匯項值為2.70×10-44kg/s。在邊界單元上施加源匯項處理水位上升引起的加載作用可以實現邊界單元上水壓力的連續變化，且比以往將水位上升過程簡化為一系列不連續的特征水位更符合實際。

在穩定滲流狀態下，各個物理量的分布狀態如圖3所示，非飽區的孔隙氣壓力水頭為0，孔隙水壓力水頭小于0，因此毛細壓力水頭小于0，在飽和區，孔隙氣壓力水頭等于孔隙水壓力水頭，毛細壓力水頭為0。觀察圖4，隨著坡外水位上升，坡外水逐漸流入土坡內部，原來被氣體填充的土壤孔隙逐漸被水填充，水飽和度逐漸增加，飽和區范圍逐漸上移，且毛細壓力水頭，孔隙水壓力水頭和孔隙氣壓力水頭均逐漸增加，其中接近土坡表面處的各物理量的變化更為顯著。由圖5表示的水位穩定后滲流場各個物理量分布情況可知，飽和區范圍繼續上移，非飽和區的水飽和度繼續增加，毛細壓力水頭、孔隙水壓力水頭和孔隙氣壓力水頭也進一步增加。

3-a 水飽和度3-b 毛細壓力3-c 孔隙水壓力3-d 孔隙氣壓力圖3 初始穩態滲流場狀態分布Fig.3 Distributions of water saturation, capillary pressure and pore pressures in initial steady state

4-a 水飽和度4-b 毛細壓力4-c 孔隙水壓力4-d 孔隙氣壓力圖4 52 h滲流場狀態分布Fig.4 Distributions of water saturation, capillary pressure and pore pressures in 52 h

圖6為追蹤面A-A在初始穩態，第52小時和第200小時的孔隙氣壓力、孔隙水壓力、毛細壓力和水飽和度分布情況。觀察圖6，水位上升以前，非飽和土體內的孔隙氣壓力為0，但是由于毛細壓力的存在，在飽和土和非飽和土的接觸面上孔隙氣壓力有一個微小的波動。水位上升過程中，隨著坡外水體流入土坡內部，孔隙氣壓力的大小逐漸增加，水位穩定后，坡外水體繼續流入土坡內部，土體內的孔隙氣壓力繼續增加。初始狀態下，土體內的孔隙水壓力水頭隨著高程的降低呈現線性增加的趨勢，在水位上升過程中和水位穩定后，隨著坡外水體流入土坡內部，孔隙水壓力水頭均在逐漸增加。毛細壓力為孔隙水壓力與孔隙氣壓力的差值，且在水位上升作用下，毛細壓力值逐漸增加。水位上升前，土坡的水飽和度隨高程的降低逐漸升高，在水位上升過程中和水位穩定后，由于坡外水流入土坡內部，土坡的水飽和度繼續增加。

圖6 初始穩態,第52小時和第200小時追蹤面A-A上的孔隙氣壓力、孔隙水壓力、毛細壓力和水飽和度分布情況Fig.6 Simulation results of pore-air pressure, pore-water pressure, capillary pressure and water saturation at section A-A at initial steady state, 52 h and 200 h

3.3 飽和-非飽和土坡穩定性分析

圖7為土坡安全系數隨時間變化過程，同時考慮孔隙氣壓力、毛細壓力、坡外水壓力和土體重力貢獻的安全系數的初始值為1.54，隨著水位的上升，安全系數逐漸增加，當水位升至21.2 m時，安全系增加至最大值2.67，水位穩定后，安全系數開始逐漸下降。不考慮孔隙氣壓力貢獻的安全系數明顯大于考慮孔隙氣壓力和毛細壓力貢獻的安全系數，其值從初始時的1.54上升到2.86后開始逐漸下降。不考慮毛細壓力貢獻的安全系數在三者中最小，其值從初始的1.06上升至2.21后開始逐漸下降。水位上升過程中，對土坡穩定性起主要作用的且有利于土坡穩定的坡外水壓力逐漸增加，使得安全系數逐漸增加；當水位穩定后，坡外水壓力保持不變，而不利于土坡穩定的孔隙氣壓力值逐漸增加使得安全系數逐漸降低。

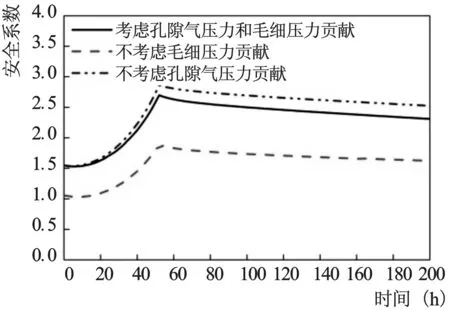
圖7 危險圓弧滑動面上安全系數 隨時間變化曲線Fig.7 Time evolution of the safety factors on the slip surface

圖8為水位上升過程中的各個力對安全系數的貢獻及作用在危險圓弧滑動面上的各個力隨時間的變化情況。由于土體自身重力在水位上升初期為1 640.40 kN/m，到模擬結束后為1 665.00 kN/m，上升了24.60 kN/m，較其自身而言，增加的重力可以忽略不計，因此土體自身重力對安全系數的貢獻幾乎不變，將不做詳細討論。

圖8-a為水位上升作用下毛細壓力對安全系數的貢獻隨時間變化的曲線及作用在危險圓弧滑動面上的總毛細壓力隨時間的變化規律。觀察圖8-a，作用在危險圓弧滑動面上總的毛細壓力值小于0，隨著水位上升毛細壓力值逐漸下降，當水位穩定后，毛細壓力值緩慢上升，因此毛細壓力對安全系數的貢獻先逐漸增加后逐漸減小，所以，安全系數圖像中不考慮毛細壓力貢獻的安全系數與考慮孔隙氣壓力和毛細壓力貢獻的安全系數的差值先逐漸增加后逐漸減小。

圖8-b為水位上升作用下孔隙氣壓力對安全系數的貢獻隨時間變化的曲線及作用在危險圓弧滑動面上總的孔隙氣壓力隨時間的變化規律。如圖8-b所示，水位上升過程中作用在危險圓弧滑動面上總的孔隙氣壓力先快速增加，即從0 kN/m增加至805 kN/m，由于孔隙氣壓力不利于邊坡穩定，總的孔隙氣壓力增加導致孔隙氣壓力對安全系數的不利貢獻從0上升至-0.16，當水位穩定后，總的孔隙氣壓力繼續由805 kN/m逐漸增加至1 068 kN/m，因此安全系數圖像中，不考慮孔隙氣壓力貢獻的安全系數與考慮孔隙氣壓力和毛細壓力貢獻的安全系數的差值先快速增加后緩慢增加。

圖8-c為水位上升作用下坡外水壓力對安全系數的貢獻隨時間變化的曲線及作用在危險圓弧滑動面上總的坡外水壓力隨時間的變化規律。水位上升過程中坡外水壓力從0 kN/m快速上升至960 kN/m，使得坡外水壓力對安全系數的貢獻從0快速增加至1.56，當水位穩定以后，由于坡外水位保持不變，因此作用在危險圓弧滑動面上總的坡外水壓力值始終為960 kN/m，坡外水壓力對安全系數的貢獻也始終穩定在1.56。

8-a 毛細壓力8-b 孔隙氣壓力8-c 坡外水壓力圖8 滑動面上各個力對安全系數的貢獻及各個力隨時間的變化過程Fig.8 Contributions to the safety factors from different kinds of pressures and different kinds of pressures acting on the slip surface

4 結論

通過建立水-氣二相流模型，研究了水位上升作用下土坡滲流場變化規律，并進一步分析了土坡穩定性變化規律，得到以下結論：

(1)將水位上升引起的飽和-非飽和滲流問題作為水-氣二相流問題研究更符合實際物理意義。從物理現象上來看，水位上升是土壤中“水驅替氣”的過程，因此，隨著水位上升，孔隙氣壓力、孔隙水壓力、毛細壓力和水飽和度均逐漸增加。

(2)岸坡的安全系數隨著水位的上升逐漸增加，水位穩定后，安全系數逐漸下降，且考慮孔隙氣壓力和毛細壓力貢獻的安全系數大于不考慮毛細壓力貢獻的安全系數，但小于不考慮孔隙氣壓力貢獻的安全系數。因此，毛細壓力的存在有利于土坡穩定，而孔隙氣壓力的存在不利于土坡穩定。

(3)水位上升作用下，毛細壓力逐漸減小，水位穩定后，毛細壓力逐漸增加，因此毛細壓力對安全系數的貢獻先逐漸增加后逐漸減小；水位上升過程中，孔隙氣壓力先快速增加，當水位穩定后，孔隙氣壓力緩慢增加，因此孔隙氣壓力對安全系數的不利貢獻先快速增加后緩慢增加；坡外水壓力逐漸增加后穩定不變，因此，坡外水壓力對安全系數的貢獻先逐漸增加后保持不變。