沉樁擠土效應對樁周土體徑向位移數值分析

李家華,單恒年,陳 祥

(中交第四航務工程勘察設計院有限公司，廣州 510230)

早在20世紀70年代，國內外學者就對沉樁擠土效應的研究做了大量的工作。歸納起來，可總結為以下幾種方法：圓孔擴張理論、應變路徑法、有限元分析法。目前對沉樁擠土效應的分析和解答大部分都是基于經典平面圓孔擴張理論[3]，在巖土工程領域中被廣泛地運用于沉樁引起的應力、孔壓和土體位移、原位測試(如旁壓試驗和靜力觸探)、爆破形成的彈坑等工程問題的分析中，另外常用的方法還有：應變路徑法、試驗方法、有限元數值模擬法等。沉樁過程樁土相互作用由于其涉及到幾何非線性、接觸非線性、材料非線性、大變形、本構模型等一系列的問題，僅僅憑借著理論公式的推導和試驗研究不足以滿足越來越精確的工程要求，以及實際施工過程中的復雜性。有限單元法(Finite Element Method)的出現，使有限元分析(Finite Element Analysis)成為了解決這些非線性復雜問題的一個有效途徑[4]。采用ABAQUS有限元分析軟件，首先建立合理的有限元模型，并與文獻中的離心試驗數據進行比較，證明模型的正確性和合理性，通過有限元模擬，研究沉樁過程中樁周土體的徑向位移變化規律。

1 沉樁有限元分析模型構建

有限元模型土體的尺寸及參數參照離心試驗來設置。假設樁徑為0.3 m,樁長為5.0 m，樁靴角度為60°，樁靴采用光滑過渡。為了減小土體邊界條件的影響，將土體的分析區域長度方向設為兩倍樁長即10 m，寬度方向設為一倍樁長即5 m，同時為了防止土體擠壓變形穿越軸線，要預留剛性小管間隙0.001 m。土體采用修正劍橋模型，模型近似尺寸設定為40，其他土體重要參數如表1所示。

表1 離心模型試驗土體參數Tab.1 Soil parameters of centrifuge test data

根據已有條件建立模型，1/2軸對稱有限元模型及網格劃分情況，模型采用Abaqus/Standard中的大變形計算，將沉樁簡化為平面軸對稱問題，通過控制分析步對樁頂施加向下位移進行模擬沉樁，最后從后處理中導出模擬結果，如圖1所示。

圖1 樁土模型(軸對稱1/2模型)Fig.1 Pile-soil model (axisymmetric 1/2 model)

1.1 土體本構模型

沉樁會使土體產生彈塑性區，即要考慮彈性區的本構模型也要考慮塑性區的本構模型。彈性部分，采用多孔介質彈性模型，它是一種非線性的各向同性彈性模型，可設置滲透系數，與孔壓單元一起使用。塑性部分，采用臨界狀態塑性模型(修正劍橋模型)。它能與彈性部分多孔介質彈性模型很好的聯合起來使用[5]，可以定義初始應力，求解孔隙水壓力的變化。模型采用相關聯流動法則，塑性勢面與屈服面相同，如果初始應力狀態點落在屈服面外側，Abaqus會自動調整初始屈服面的位置。

1.2 荷載邊界條件

在初始分析步ini(Gesostatic分析步)中設置Body Force(體力)為浮重度-9 kN/m3。對于單樁貫入的問題，樁的貫入通過樁頂參考點RP施加向下的位移來模擬，樁頂位移可在初始應力平衡后的后續分析步中施加，在初始分析步中，U1、U2及UR3均設置為0。另外，在土體中心線處的邊界條件設置也需要特別注意。本模型簡化為平面軸對稱問題來求解，因此不能發生穿越中心線的情況發生，但是遠離樁中心線可以發生擠土效應，簡單起見，采用一個很實用的方法來解決這個問題：在樁的底部加上一個直徑為1 mm的剛性小管，沿著小管的法線方向，不能承受拉力，可模擬土體開裂，阻止土體穿越中心線的位移產生。同時，還需要定義土體底面的水平和豎向位移均為0，定義土體右側的水平位移為0，土體左側的邊界條件由接觸條件來控制，無須設置，土體的邊界條件在初始分析步ini中定義生效。

1.3 平衡初始應力

定義初始應力需要注意兩個方面：首先是平衡條件，為了得到初始位移為0的狀態，應力場形成的等效節點荷載要和外荷載相平衡；其次是屈服條件，初始應力場若通過高斯點的應力狀態來施加，往往會出現一些高斯點的應力狀態落在屈服面之外，雖然在后續的計算當中，超出屈服面的應力可以通過應力來調整，但畢竟是不正確的，需要消耗大量的迭代，甚至可能出現不收斂的情況。基于以上兩方面條件，常用的平衡初始應力方法是[6]：首先將重力荷載施加于土體，并施加相應的實際工程荷載和邊界條件，計算在重力載荷下的應力場，再將此應力場定義為初始應力場與原重力荷載一起施加在有限元模型上，這樣就可以得到滿足平衡條件且不違背屈服準則的初始應力場，保證各節點的初始位移接近為0。若地表是水平的，則可以極大的減少定義初始應力的工作量。

1.4 接觸問題

由于接觸面的不連續約束及力學模型本身的非線性，在數值模擬中常常會出現不收斂的情況。Abaqus采用的主-從面接觸法，一個完整的接觸模擬首先需要定義主控面(master surface)和從屬面(slave surface)，然后再定義它們的接觸狀態，接觸屬性等。由于本模型絕大部分涉及到接觸問題，不允許土體穿透中心線，所以采用點對面的離散法，更易收斂。

1.5 網格ALE技術

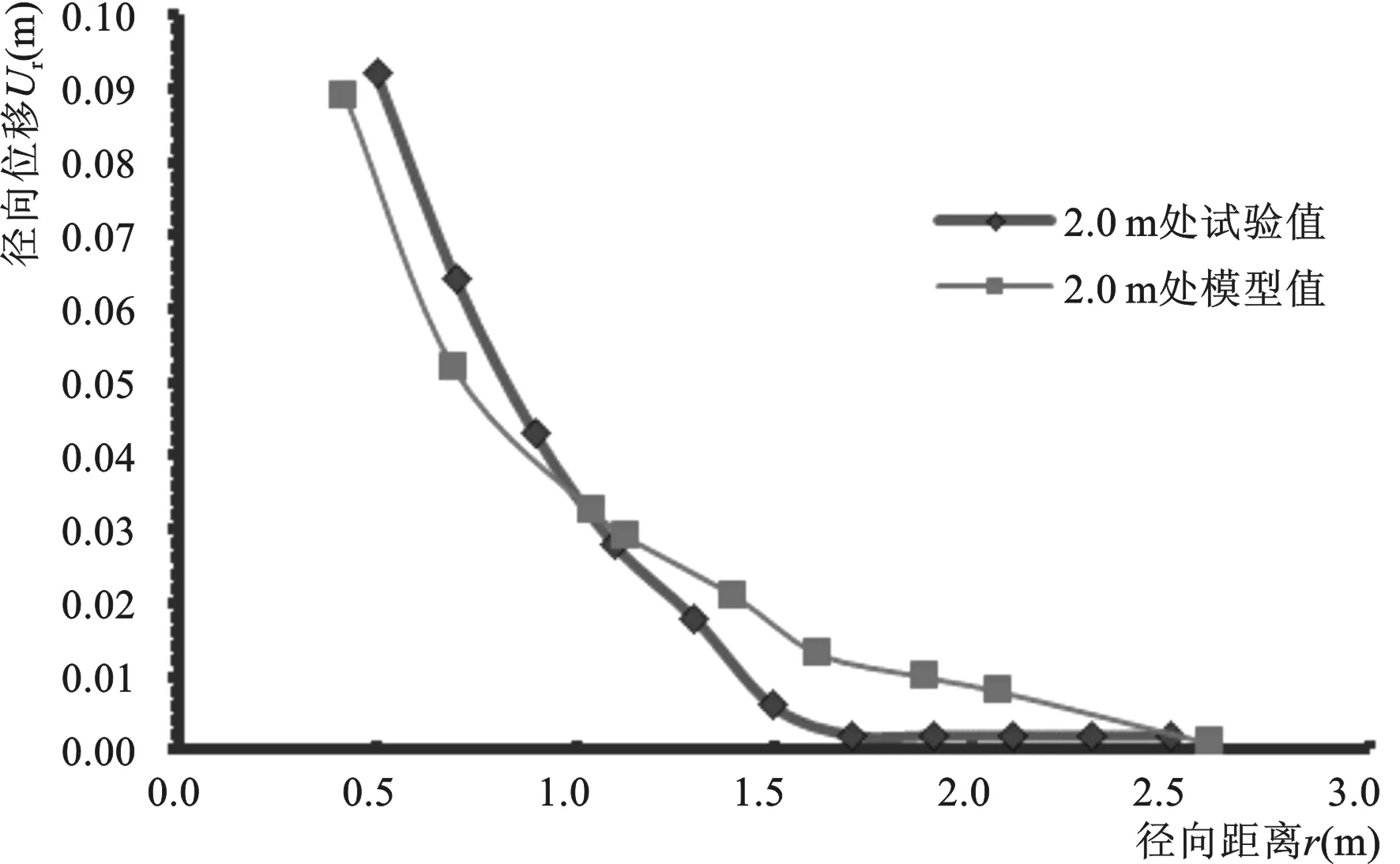
圖2 深度2.0 m處樁側土體水平位移試驗值 與模型值比較圖Fig.2 Comparison of horizontal displacement test value and model value of pile soil at depth 2.0 m

靜壓樁沉入的過程中，在樁尖及樁端處存在著大應變、大變形，網格將會扭曲的很明顯，隨著樁的沉入，邊界條件也在不斷的改變，位移的模式實際上是跳躍的，需要重新去確定邊界問題，比較難收斂。在有限元軟件Abaqus中，提供了一系列自適應的技術，如任意拉格朗日-歐拉法自適應網格劃分技術(Arbitrary Lagrangian Eulerian adaptiove meshing)等用來處理高度扭曲的網格。ALE分析步可以分為兩個步驟：(1)創建一個新的網格；(2)將舊網格的變量信息，其中包括應力場、應變場與動變量等，傳輸到新網格上。這樣做可以使網格與物質相分離，即使發生了網格大變形，也能保證在分析計算中網格的高質量。ALE技術與原網格有一定的相關性，所以要保證初始網格才能提高ALE技術的效率。由于靠近中心線的土體區域是高應變區，網格的扭曲很嚴重，所以在分析步中設置ALE區域位于離軸線2 m的矩形區域，同時分別設置自適應技術里的頻率控制與對數控制。頻率控制(Frequency)主要是對每個分析步時間步長里網格的重劃分次數控制，對于拉格朗日問題，默認參數為10，對歐拉問題，默認值為1，本模型選用1；參數控制(Mesh Sweeps)是對整個自適應重劃分的每個子過程的控制，需要在新網格的基礎上再進行sweep，本模型選用1。使用ALE技術會對輸出結果帶來一定的影響，在未使用ALE網格劃分技術時，物質點與網格點在計算過程中是保持相互重合的，使用完之后，網格的節點的位移將不能表示物質點的位移狀態變化，而是物質點移動與網格重劃分共同影響的，也就是說節點處的位移將不代表物質點真實的位移，所有位移的云圖變化將不再是準確的，而歷史變量隨時間的變化也都是無效的。

1.6 驗證有限元模型

在有限元模型中對樁頂參考點施加向下的位移5 m，時間步設為500 s，近似模擬1 cm/s的沉樁速率，與離心模擬試驗沉樁速率相符，由于設備有限，離心試驗[2]只對土體位移和孔壓進行了研究，完成后的模型數據與離心試驗數據比較，2.0 m深處樁側土體水平位移試驗值與模型值分布如圖2所示。

可以看出，模型值與試驗值具有類似的分布規律，且誤差在允許范圍內，證明了有限元模型的合理性，可以借助該模型進行進一步的研究。

2 沉樁過程土體徑向位移變化規律有限元分析

2.1 沉樁過程土體徑向位移變化規律

利用有限元模型模擬沉樁過程，分析沉樁至不同深度時土體徑向位移變化規律，如圖3所示。

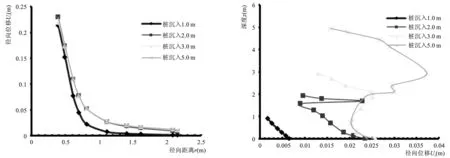
3-a 沉樁過程中土體表面徑向位移變化3-b 沉樁過程徑向距離r=2 d(d為樁直徑)處深度方向徑向位移變化圖3 沉樁過程土體徑向位移模型數值變化圖Fig.3 Numerical simulation of soil radial displacement model during pile driving

由圖3分析可知：(1)地表的土體被樁向外擠出，徑向位移Ur且隨徑向距離r的增大呈對數衰減，且靠近樁的地方，擠土效應更加明顯，衰減越快。隨著樁體的沉入，土表面徑向位移增加不大，保持對數衰減的趨勢；(2)沿深度方向，徑向位移有減小的趨勢，但在樁端以上0.5～1.5 m處達到最大值。Jim-HungHwang[7]等人在1994年通過觀測發現這個距離為10d，原因在于本文取的是均質土層，而實際土質并非是均勻的，并且在沉樁的過程中，土體也在不斷的重組，位移也在發生著變化。

2.2 土體參數對土體徑向位移影響

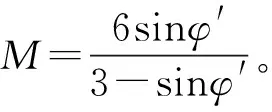
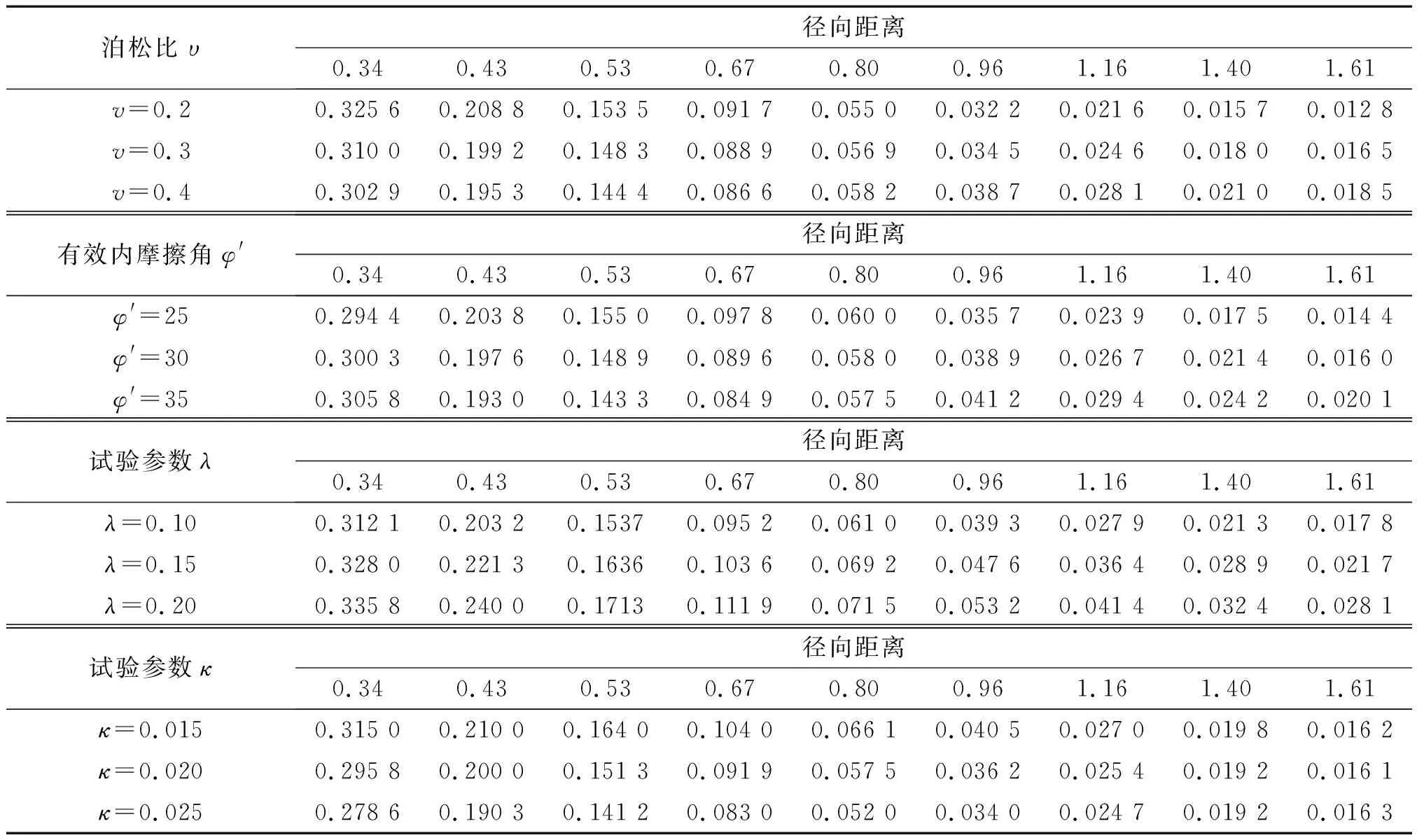
表2 沉樁過程不同參數下樁周土體徑向位移值Tab.2 Radial displacement of soil around pile in different parameters of pile driving process m

整埋數據，可得到沉樁過程樁周土體的徑向位移變化規律，如圖4。

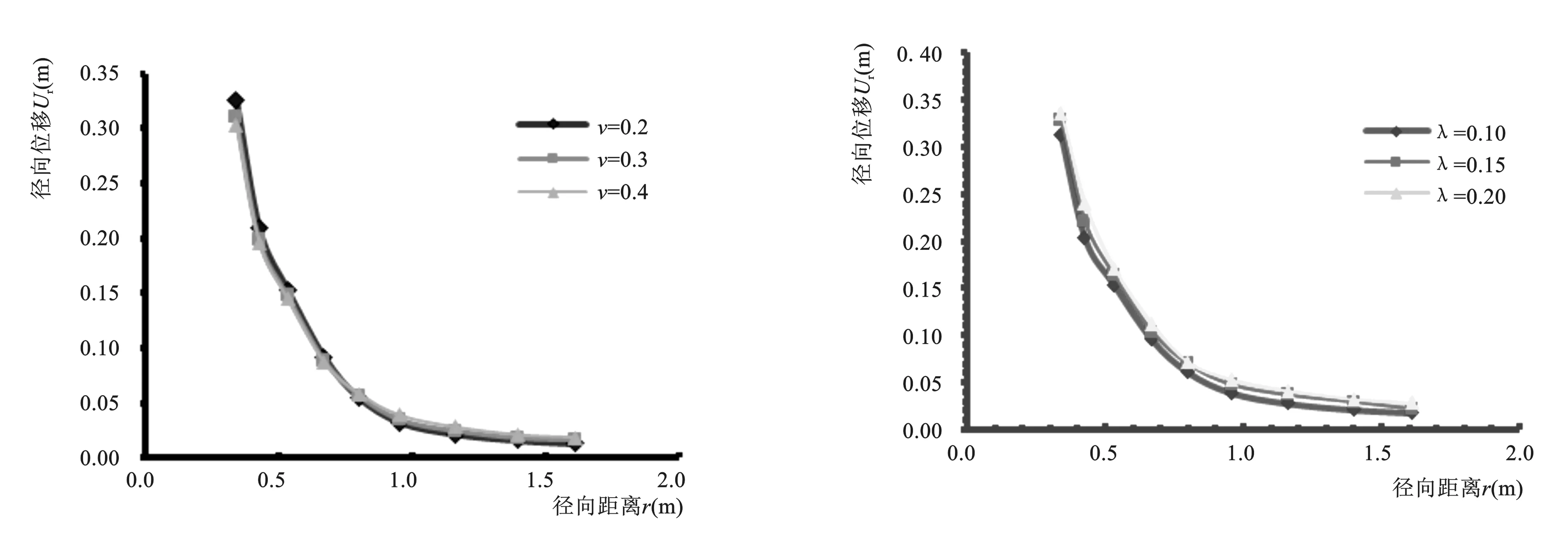
4-a 泊松比υ對徑向位移的影響 4-b 試驗參數λ對徑向位移的影響

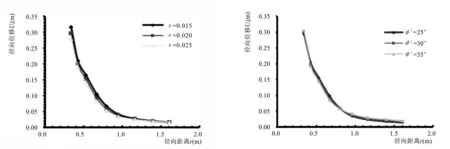
4-c 試驗參數κ對徑向位移的影響 4-d 有效內摩擦角φ′對徑向位移的影響圖4 沉樁過程不同土體參數下樁周土體徑向位移值變化規律Fig.4 Variation law of radial displacement of soil around the pile under different soil parameters during the process of pile driving

分析可得：(1)在距離樁入土較近的區域，土體徑向位移受泊松比影響不大，但是隨著徑向距離的增大，泊松比開始影響土體的徑向位移，泊松比越大，徑向位移也越大；(2)試驗參數λ、κ是劍橋模型中各向等壓加荷曲線和卸荷曲線的斜率，當λ增大時，徑向位移以一定的幅度增大，當κ增大時，則徑向位移相對減小，遠離樁向的土體徑向位移基本不受影響；(3)有效內摩擦角φ′在修正劍橋模型中存在的形式較為復雜，所以影響規律也不是單調的增加或減少，在徑向距離較小時有效內摩擦角的改變影響不大，在0.4～0.8 m的范圍內，有效內摩擦角的增大，徑向位移相應減小，而在0.8 m以外有效內摩擦角增大，徑向位移相應增大。

3 結語

關于樁的擠土效應的研究一直以來都是學者們關注的焦點，從理論推導到試驗研究再到現在的數值模擬，仍處在不斷的發展中。關于沉樁擠土效應機理的研究更是因其特殊性而成為樁土相互作用研究的重中之重，結合離心模擬試驗的結果，利用Abaqus有限元分析軟件建立沉樁模型，將模型計算得到徑向位移值與試驗檢測出來的水平位移值進行比較，驗證模型的合理性，同時對沉樁過程樁側土體的變形特性進行分析，為施工設計提供借鑒，具有很大的理論意義和實際意義。本文將沉樁簡化為平面軸對稱問題，利用Abaqus有限元軟件建立沉樁模型，通過控制分析步對樁頂施加向下位移進行模擬，最后從后處理中導出模擬結果。沉樁過程中，樁周土體被擠開，徑向位移比較大的區域主要集中在樁附近，并隨著與樁中心距離增加而對數衰減，到一定范圍之后則沒有什么影響。在沿沉樁的深度方向，徑向位移并不是線性增大，而是在樁底以上一定距離處達到最大值，這主要是受到土體重組的影響。另外，本文也研究了土質參數對沉樁時土體徑向位移的影響，它與有限元模型中所采用的土體模型密切相關，在不同區域范圍里，具有各自變化的規律，其中，泊松比系數在徑向距離大于1 m時才開始顯著影響徑向位移的大小；試驗參數λ增大時，土體徑向位移也隨之增大；試驗參數κ則相反；有效內摩擦角φ′對土體徑向位移的影響規律較為復雜，在0.4～0.8 m的范圍內，有效內摩擦角的增大，徑向位移相應減小，而在0.8 m以外有效內摩擦角增大，徑向位移相應增大。