基于直覺模糊集下的工程評標研究

董明娟

（廣東天聯電力設計有限公司，廣東廣州，510663）

1 定義

1.1 模糊集

定義2.1[1]設X是一個非空集，則X上的模糊集A定，其中，μA(x)∈ [0,1]，稱μA為x的隸屬度，1-μA為x的非隸屬度，函數μA( x)為x的隸屬函數。為了方便起見，模糊集簡記為{μA}。

在實際決策問題中，由于客觀事物的復雜性、信息的不確定性及決策者思維的模糊性，采用模糊集往往不能很好地反映決策者的主觀意愿和決策意見。為此，保加利亞學者Atanassov將模糊集進行了拓展和推廣，于1986年提出了直覺模糊集，它增加了一個新的屬性參數—猶豫度，更加完整地刻畫了客觀世界的模糊性本質，比傳統的模糊集更具靈活性和實用性[1]。

定義2.2[1]設X是一個非空集，則X上的直覺模糊集和分別為X上元素x∈A的隸屬度和非隸屬度，且滿足。為了方便起見，直覺模糊集簡記為。

1.2 多屬性決策方法

1.3 直覺模糊c均值聚類算法

模糊c均值聚類算法主要是通過優化基于某種范數和聚類原形的目標函數得到每個待分類對象對所有聚類中心的隸屬度，從而決定分類對象的類屬以達到自動進行分類的目的[2]。

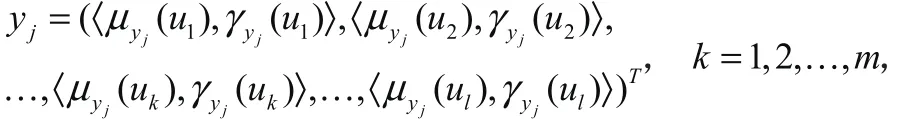
那么分類對象集合可表示成一個n×l的矩陣，即：Y =(〈 μjk, γjk〉 )n×l。相應地，每一個聚類中心 vi可表示為 ：

V =(〈 μki, γki〉 )l×c。因此，分類對象 xj與聚類中心 vj之間的模糊分類矩陣可表示為：P = ( μij)c×n。由模糊c均值聚類算法可知，直覺模糊c均值聚類算法的目標函數為：

其中，m＞1是模糊系數，一般取2；μij是第j個分類對象 yj屬于第i類的隸屬度值；dij( yj, vi) 表示從樣本點yj到中心 vi的距離，本文采用直覺模糊集的歐式距離，即個關于自變量(,)PV 約束……