基于數(shù)字圖像的自適應(yīng)多機(jī)動(dòng)目標(biāo)模型跟蹤方法

劉鋼，王蓉暉

（1.空軍航空大學(xué)基礎(chǔ)部，吉林長(zhǎng)春，130022；2.吉林建筑大學(xué)電氣與計(jì)算機(jī)學(xué)院，吉林長(zhǎng)春，130018）

1 幾種典型的機(jī)動(dòng)目標(biāo)模型

1.1 辛格模型

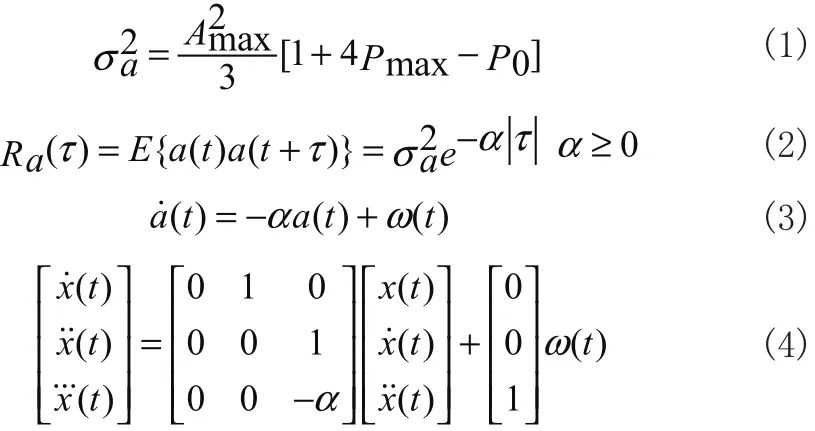
1.2 當(dāng)前狀態(tài)統(tǒng)計(jì)模型

其中a(t)為機(jī)動(dòng)加速度當(dāng)前均值，在每一采樣周期內(nèi)為常數(shù)。

把上式帶入一階時(shí)間相關(guān)方程，可得：

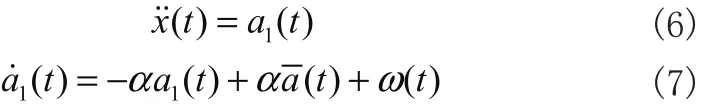
將上式寫(xiě)為狀態(tài)方程，即為機(jī)動(dòng)目標(biāo)“當(dāng)前”統(tǒng)計(jì)模型：

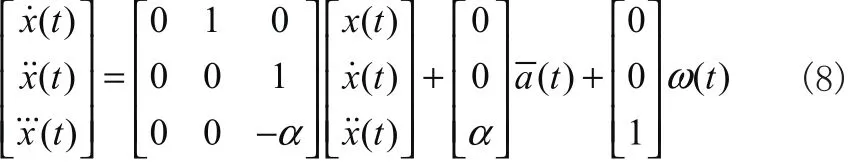
1.3 階躍模型

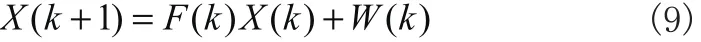
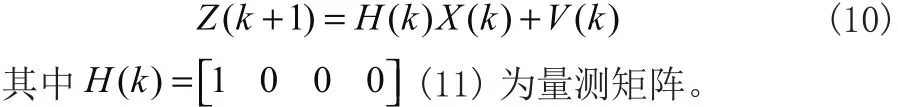
W(k)和 V (k)是不相關(guān)的高斯白噪聲序列。F (k)為狀態(tài)轉(zhuǎn)移矩陣，表達(dá)式為：

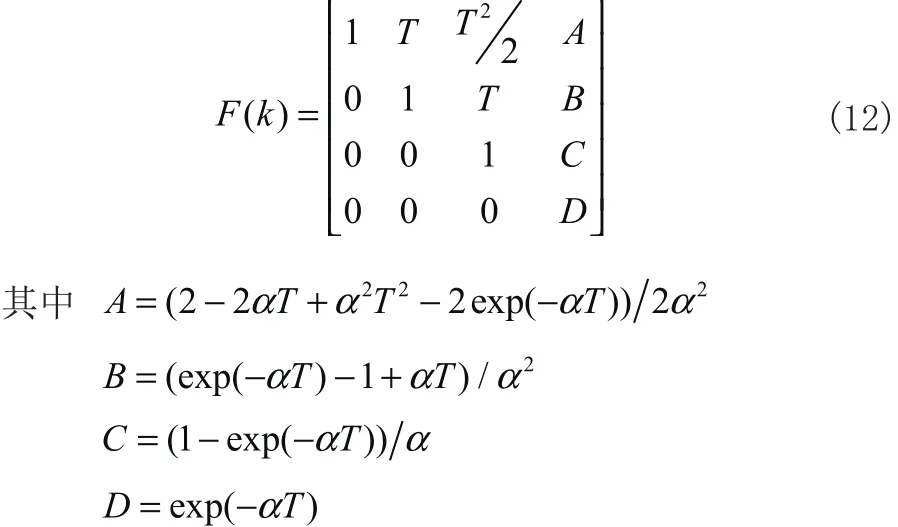
2 Monte Carlo仿真實(shí)驗(yàn)

在常加速度情況下，比較辛格模型和當(dāng)前狀態(tài)統(tǒng)計(jì)模型，進(jìn)行目標(biāo)加速度估計(jì)。這里α=0.1，T=1s，a = 2 0 m /s2，時(shí)間是在 t = 0 ～100s，圖1中實(shí)線和離散點(diǎn)分別描繪的是當(dāng)前狀態(tài)統(tǒng)計(jì)模型和辛格模型的加速度統(tǒng)計(jì)。辛格模型的均方根誤差為2.83，均值誤差為0.59；當(dāng)前狀態(tài)統(tǒng)計(jì)模型的均方根誤差為1.95，均值誤差為-0.14。

如圖2所示，變加速機(jī)動(dòng)不適合辛格模型。所以在這里比較了當(dāng)前狀態(tài)統(tǒng)計(jì)模型和階躍模型。圖2是在變加速度情況下，進(jìn)行目標(biāo)加速度估計(jì)。如圖2中離散點(diǎn)描繪的是階躍模型的加速度統(tǒng)計(jì)，實(shí)線描繪的是當(dāng)前狀態(tài)統(tǒng)計(jì)模型的加速度統(tǒng)計(jì)。階躍模型的均方根誤差為3.64，均值誤差為0.92，當(dāng)前狀態(tài)統(tǒng)計(jì)模型的均方根誤差為2.86，均值誤差為-0.34。

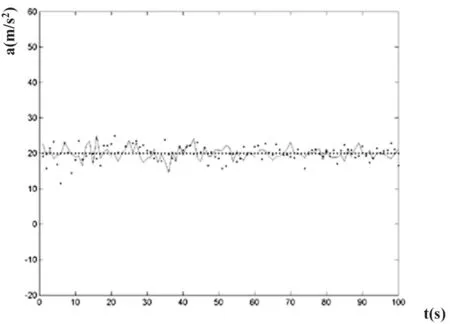
圖1 常加速運(yùn)動(dòng)的目標(biāo)加速度估計(jì)

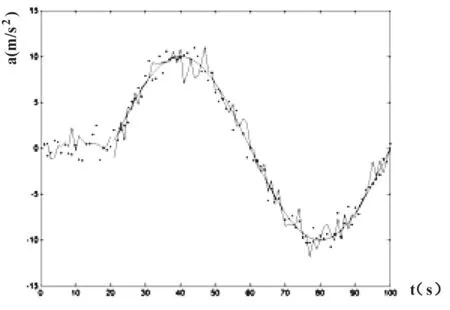
圖2 變加速運(yùn)動(dòng)的目標(biāo)加速度估計(jì)

下面比較了當(dāng)前狀態(tài)統(tǒng)計(jì)模型和階躍模型。這里α=0.1，T= 1 s，如圖3中離散點(diǎn)描繪的是當(dāng)前狀態(tài)統(tǒng)計(jì)模型的加速度統(tǒng)計(jì)，實(shí)線描繪的是階躍模型的加速度統(tǒng)計(jì)。階躍模型的均方根誤差為4.78，均值誤差為1.65；當(dāng)前狀態(tài)統(tǒng)計(jì)模型的均方根誤差為6.23，均值誤差為-1.82。……