面內載荷作用下功能梯度板動力屈曲

王 鑫，龍夢璇，韓志軍，吳亞麗

(太原理工大學 a.力學學院，b.建筑與土木工程學院，太原 030024)

功能梯度材料是由兩種或多種材料構成的新型復合材料，具有不同材料之間呈現光滑連續的特性，可以有效避免傳統復合材料因材料屬性微觀不均勻而引起的應力集中以及分層、開裂等現象。功能梯度材料由于優越的力學性能而備受學術界關注[1-2]，在航空航天、機械工程、生物醫學工程以及核工程等諸多領域得到了廣泛應用，科研人員對功能梯度板的動力屈曲的探究也不斷深入[3-4]。FELDMAN et al[5]研究了功能梯度板在面內載荷作用下的彈性動力屈曲，并給出了增強項的最佳空間分布。LATIFI et al[6]基于經典板理論，采用傅里葉級數展開研究了各種邊界條件下面內載荷矩形功能梯度板的動力屈曲。BODAGHI et al[7]采用細觀力學模型，給出了簡支條件下非均勻分布面內動力載荷矩形功能梯度板屈曲解析表達式。NG et al[8]基于經典板理論，討論了功能梯度圓柱殼和矩形板在面內周期載荷作用下的動態屈曲。KOWALMICHALSKA et al[9]采用經典板理論通過有限元法獲得了含有裂紋的功能梯度板臨界屈曲載荷。RAD et al[10]基于經典板理論，通過有限元法研究了含初始缺陷的功能梯度板的屈曲問題。KHORSHIDI et al[11]基于經典板理論，研究了考慮指數剪切變形下功能梯度納米板的屈曲。 MANTARI et al[12]基于經典板理論和雙曲線優化方程，對功能梯度夾層板在面內載荷作用下的動力屈曲、振動以及彎曲進行了分析。

綜上所述,目前對功能梯度板屈曲問題的研究大多采用數值解法和計算機仿真。基于此，本文使用Kirchhoff薄板理論與Vogit應變假設，用Hamilton原理得到各項物性參數服從冪律分布的功能梯度板的動力屈曲控制方程；用分離變量法及試函數法，得出功能梯度板滿足邊界條件的動力屈曲臨界載荷解析表達式，與用棣莫弗公式結合李茲法得到的動力屈曲臨界載荷相同。運用MATLAB軟件編程對臨界載荷解析表達式進行數值計算，討論了功能梯度板的幾何尺寸、梯度指數、模態階數以及構成材料的各項物性參數對臨界載荷的影響。

1 功能梯度材料的物性參數

基于Vogit等應變假設及線性混合率，假定功能梯度板各項物性參數僅沿厚度方向變化，陶瓷材料體積率遵循冪律分布[13-14]：

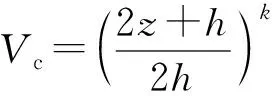
(1)

則板內任意一點的物性參數可表示為:

(2)

2 控制方程推導

功能梯度板在x=0處為夾支邊界條件，在x=Lcr處為固支邊界條件，在y=0和y=Lb處為簡支邊界條件，此類板簡稱CFSS板，如圖1所示。

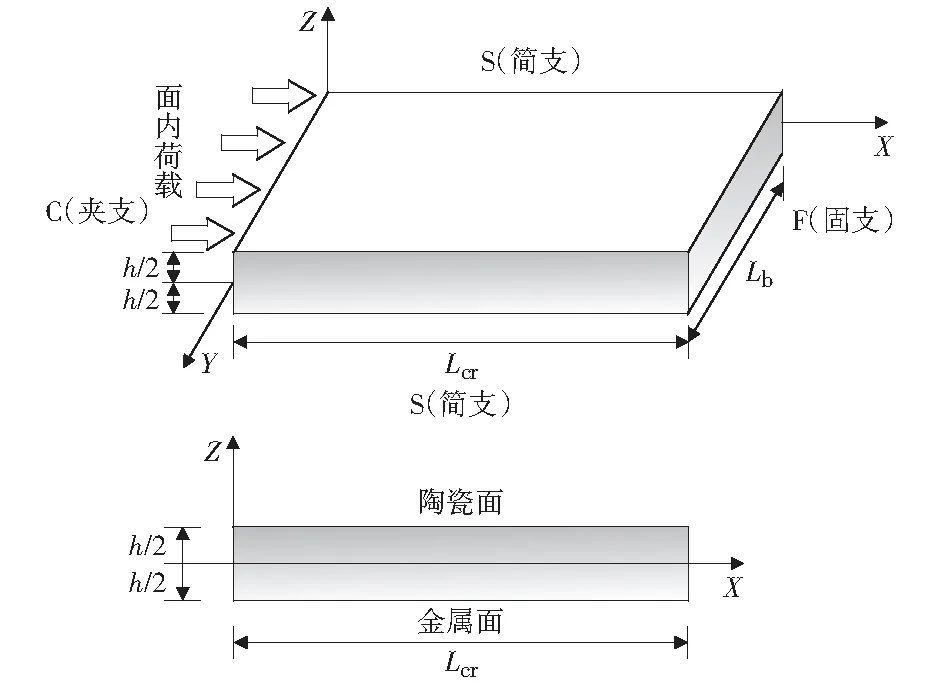
圖1 CFSS功能梯度板加載示意圖Fig.1 CFSS functionally graded material plate under the in-plane load

根據Kirchhoff薄板理論及經典彈性理論，位移與應變關系為：

(3)

功能梯度材料的本構關系為：

(4)

功能梯度板的內力及內力矩為：

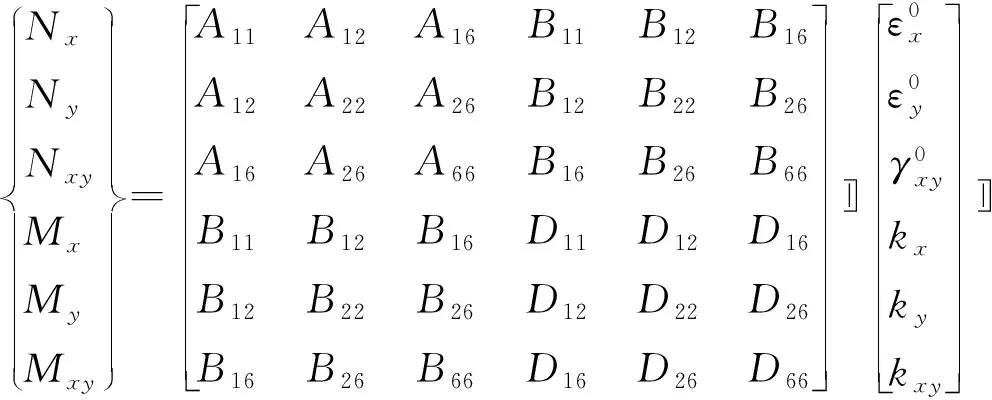
(5)

功能梯度板的剛度矩陣的系數表達式為：

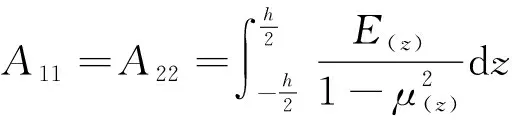
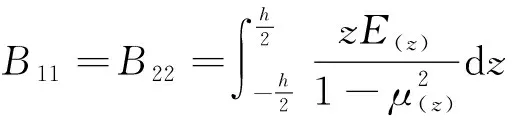
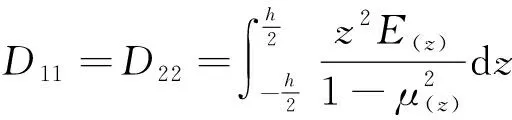
(6)

功能梯度板具有橫觀各項同性的力學性能[15]，可知：

A16=A26=B16=B26=D16=D26=0 .

(7)

功能梯度板發生屈曲時的變形能為：

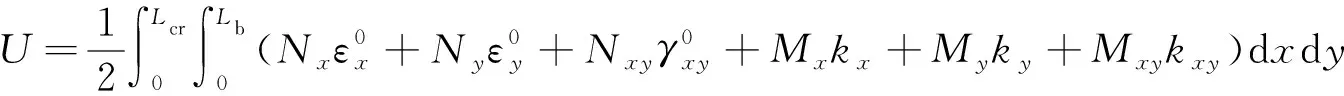
(8)

動能(考慮轉動慣量)為：

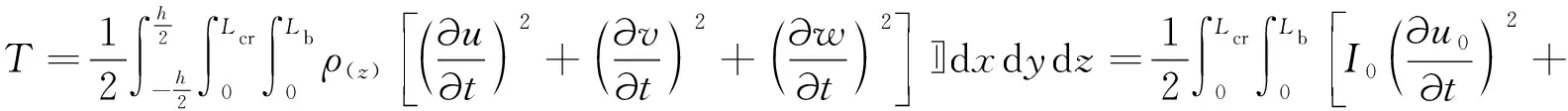
(9)

式(9)中定義廣義慣量為:

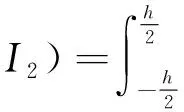
(10)

外力功為：

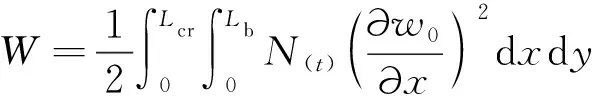
(11)

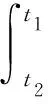
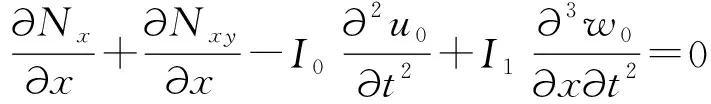
(12)

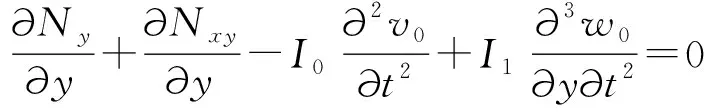
(13)

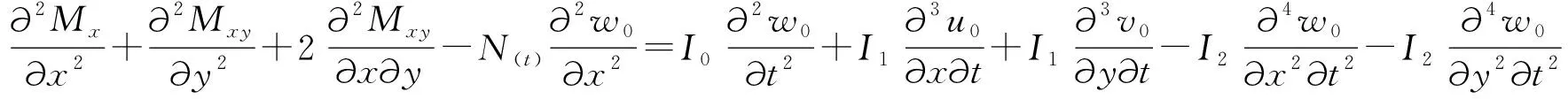
(14)

將式(5)代入式(12)-式(14)可得：

根據Kirchhoff薄板理論，薄板中面在變形過程中沒有伸長變形，所以含u0,v0的項可以忽略[16]，得出功能梯度材料在面內載荷作用下的動力屈曲控制方程：

D11wxxxx+(2D22+4D66)wxxyy+D11wyyyy+N(t)wxx-I0w+I2wxx+I2wyy=0 .

(16)

3 控制方程的求解

設薄板平面的法向位移為[17]：

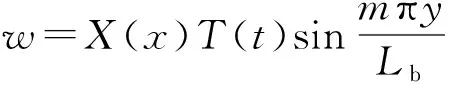
(17)

代入控制方程化簡可得：

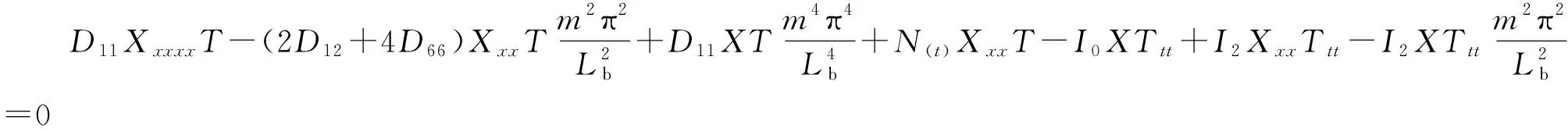
(18)

對式(18)分離變量可得：

(19)

式中：

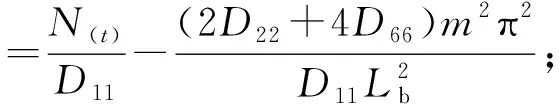
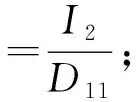
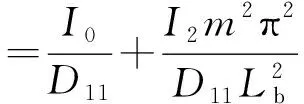
當λ<0時，其解為指數型發散解，系統呈現不穩定狀態。當λ>0時，系統圍繞平衡位置做微小擾動[18]。所以當λ<0,(α-λξ)2-4(β-λξ)>0時，平板發生屈曲，其動力屈曲解為：

X(x)=C1sink1x+C2cosk1x+
C3sink2x+C4cosk2x.

(20)

式中：

式(20)滿足下列一端夾支、一端固定、另外兩端簡支功能梯度材料板的邊界條件：

(21)

將式(20)代入式(21)中得：

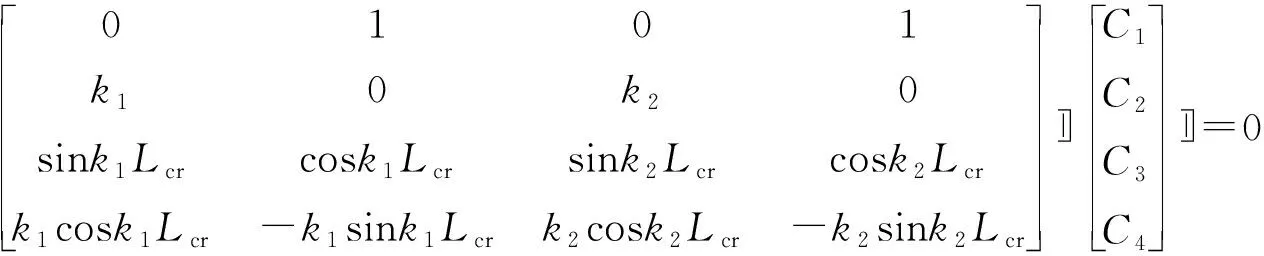
(22)

若該方程有非奇異解，其系數行列式必為0.可得：

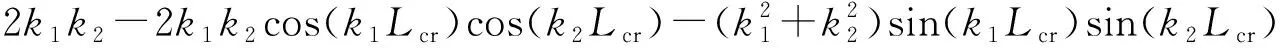
(23)

分析該式可得：

(24)

由式(24)可得一端夾支、一端固定另外兩端簡支板臨界屈曲載荷為：

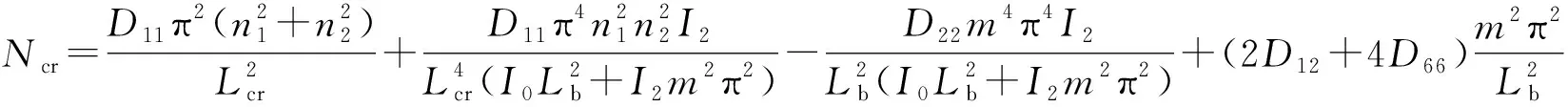
(25)

式中：n1=1,2,3,…;n2=n1+2;m=1,2,3,….由式(17)、式(20)、式(21)聯立求解，得屈曲解表達式：

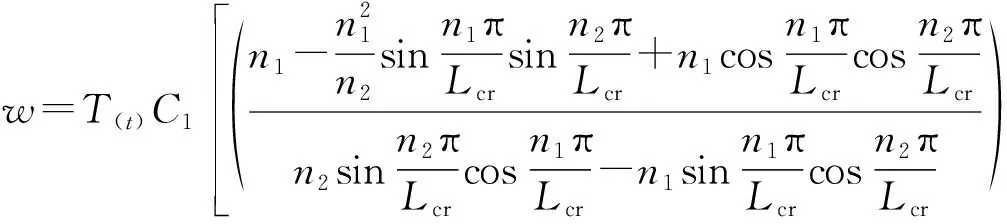
(26)

用里茲法和棣莫弗公式結合計算CFSS板動力屈曲[15]，根據邊界條件可取：

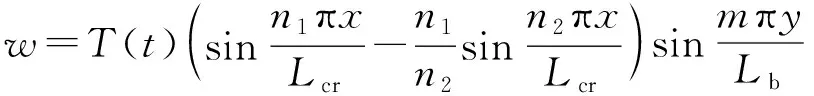
(27)

式中：n1=1,2,3,…;n2=n1+2;m=1,2,3,… .將式(27)代入控制方程式(16)，經化簡運算，得到臨界載荷表達式為：

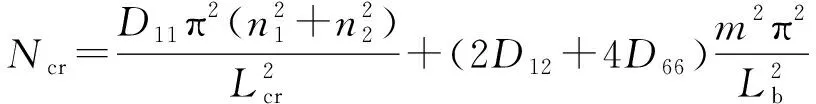
(28)

該方法所得結果與本文中式(25)不考慮轉動慣性的動力屈曲臨界載荷結果相同。

將功能梯度板梯度指數k值取為0，根據冪律分布及物性參數表達式(1)、式(2)，功能梯度材料蛻化為單質金屬材料。臨界屈曲載荷表達式化簡為：

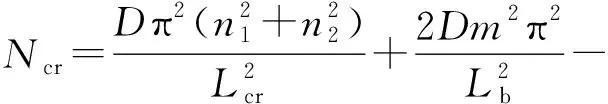
(29)

4 數值計算

本文應用MATLAB軟件編程對式(25)計算分析，以CFSS功能梯度矩形板為例，加載方式與幾何尺寸見圖1，具體材料參數取值見表1.

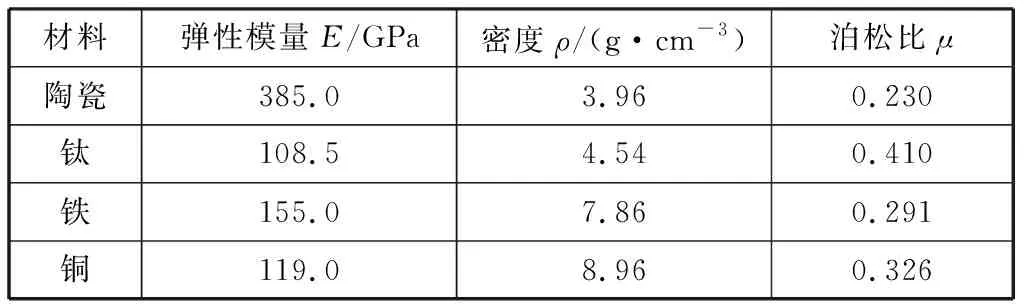
表1 材料各項物性參數Table 1 Physical parameters of component materials

圖2是當CFSS功能梯度板的寬度Lb、厚度h、梯度指數k、X方向模態數m、Y方向模態數n相同，構成材料不同時，動力屈曲臨界載荷Ncr與臨界長度Lcr的關系曲線。

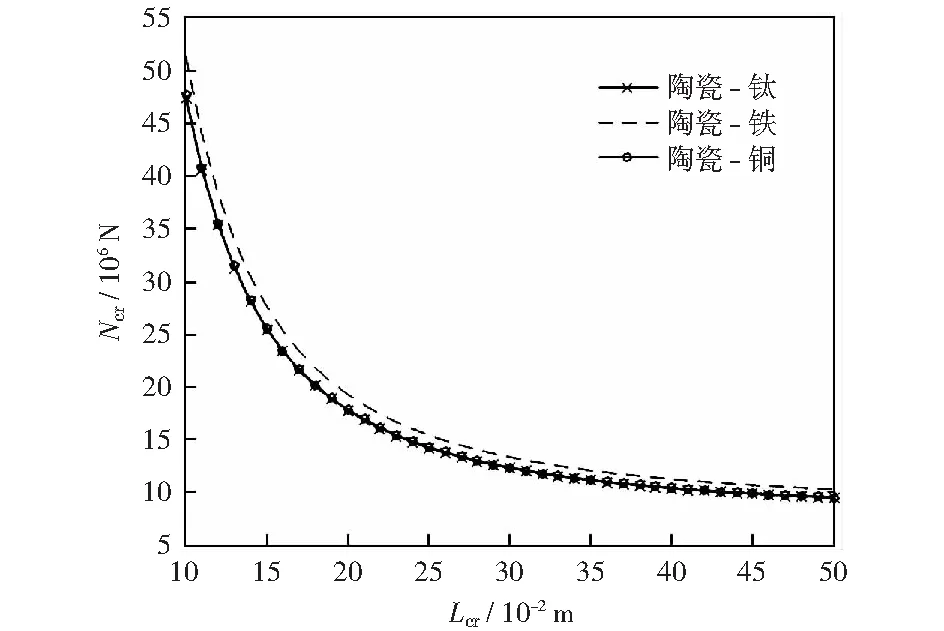
圖2 構成材料不同時臨界載荷與臨界長度的關系Fig.2 Relationship between the critical load and length when material is different

圖2表明，Ncr隨Lcr的增加呈指數式下降。當Lcr相同時，(陶瓷-鐵)板的臨界載荷高于(陶瓷-鈦)板，而(陶瓷-鈦)板與(陶瓷-銅)板的臨界載荷曲線幾乎重合。參照表1，材料鈦和鐵的彈性模量差距較大，材料鈦和銅泊松比差距較大。結合圖2和表1數據分析可得：材料的彈性模量變化對功能梯度板動力屈曲臨界載荷的影響較為明顯，泊松比影響相對較小。

圖3是當CFSS功能梯度板的h、k、m、n與構成材料相同，Lb不同時，Ncr與Lcr的關系曲線。

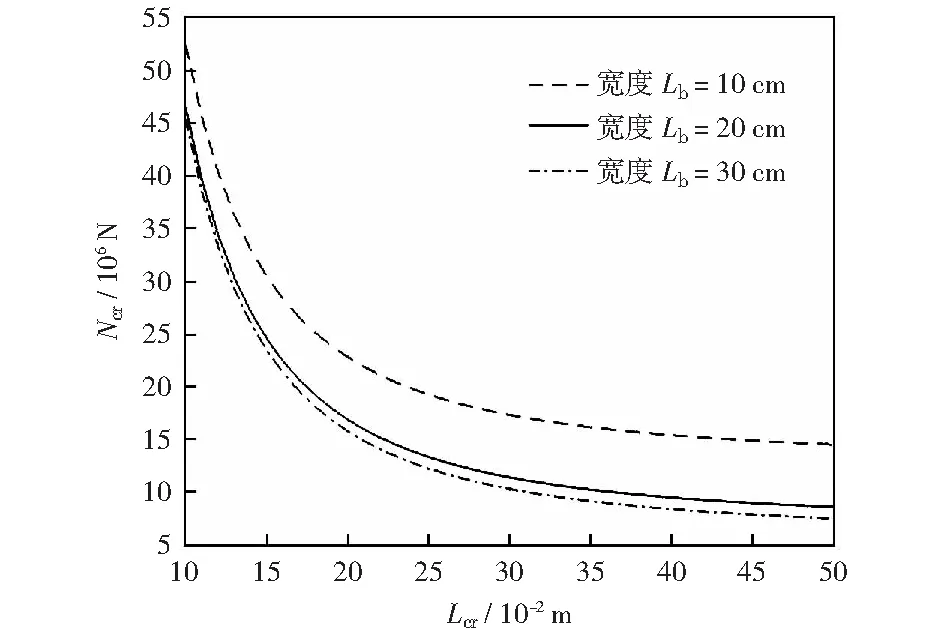
圖3 寬度Lb不同時臨界載荷與臨界長度的關系Fig.3 Relationship between the critical load and length when width is different

由圖3可知，當Lcr相同時，Ncr隨Lb的增大而減小。當功能梯度材料板的長寬比小于1/2時，Ncr隨Lcr變化明顯；大于1/2時，Ncr隨Lcr的變化趨于平緩。

圖4是當CFSS功能梯度板的Lb、h、m、n與構成材料相同，k不同時，Ncr與Lcr的關系曲線。當Lcr相同時，Ncr隨k的增大而減小。k越小，Ncr隨Lcr的變化越明顯，k值在(0，1)的范圍內變化對Ncr的影響較大。不同k值對應的臨界載荷曲線隨Lcr的增加逐漸趨于水平。

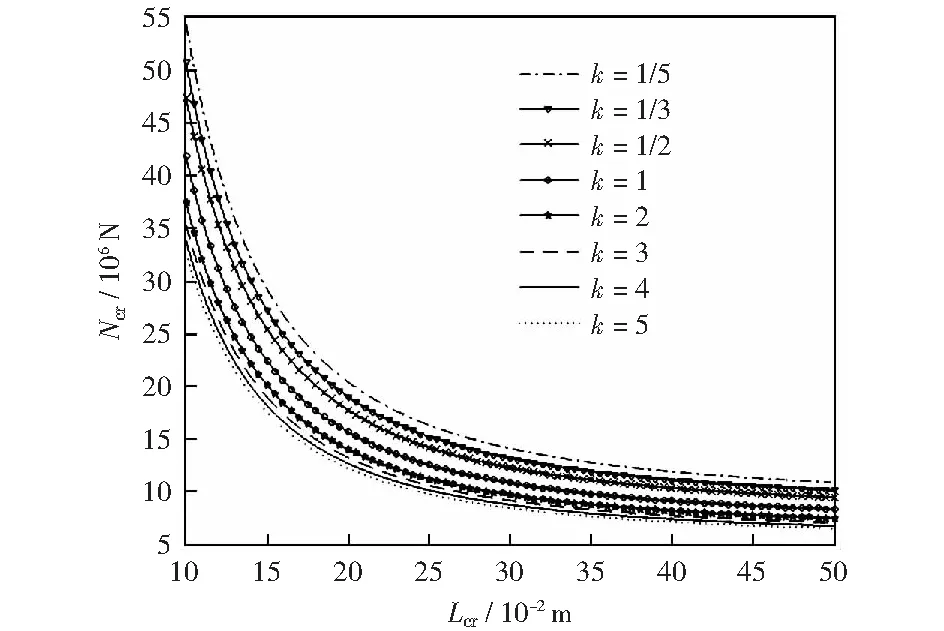
圖4 梯度指數k不同時臨界載荷與臨界長度的關系Fig.4 Relationship between the critical load and length when gradient index is different

圖5是當CFSS功能梯度板的Lb、h、k、m與構成材料相同，n不同時，Ncr與Lcr的關系曲線。當Lcr相同時，Ncr隨n的增大而增大，n值越高，Ncr隨Lcr變化越明顯，表明臨界載荷越大，功能梯度板的高階屈曲模態越容易被激發。當臨界長度達到一定值時，不同的X向模態數對應的臨界載荷逐漸趨于一定值。

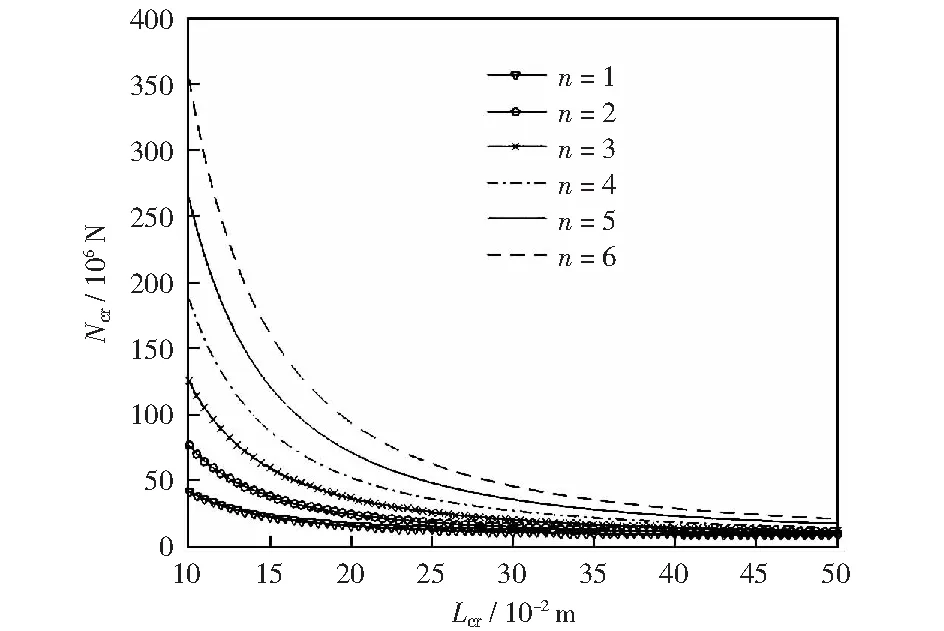
圖5 X方向模態數n不同時臨界載荷與臨界長度的關系Fig.5 Relationship between critical load and length when the modal number of X direction is different

圖6是當CFSS功能梯度板的Lb、h、k、n與構成材料相同，m不同時，Ncr與Lcr的關系曲線。當Lcr

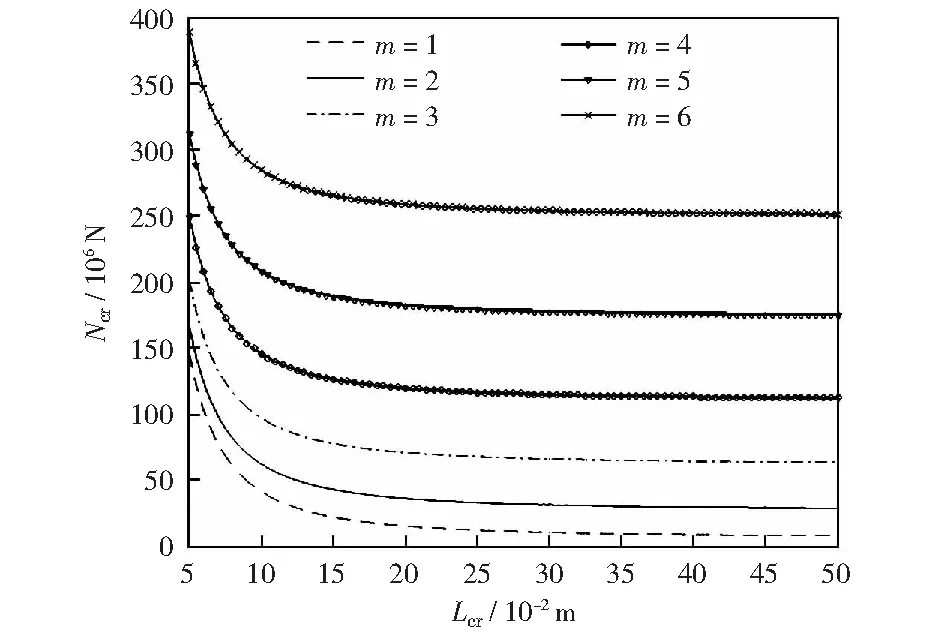
圖6 Y方向模態數不同時臨界載荷與臨界長度的關系Fig.6 Relationship between critical load and length when the modal number of Y direction is different

相同時，Ncr隨m的增大而增大，且m越大，相鄰模態數對應的Ncr差值越大，不同m值對應的曲線隨Lcr的增大逐漸趨于水平。這也表明：臨界載荷越大，越容易激發高階模態。

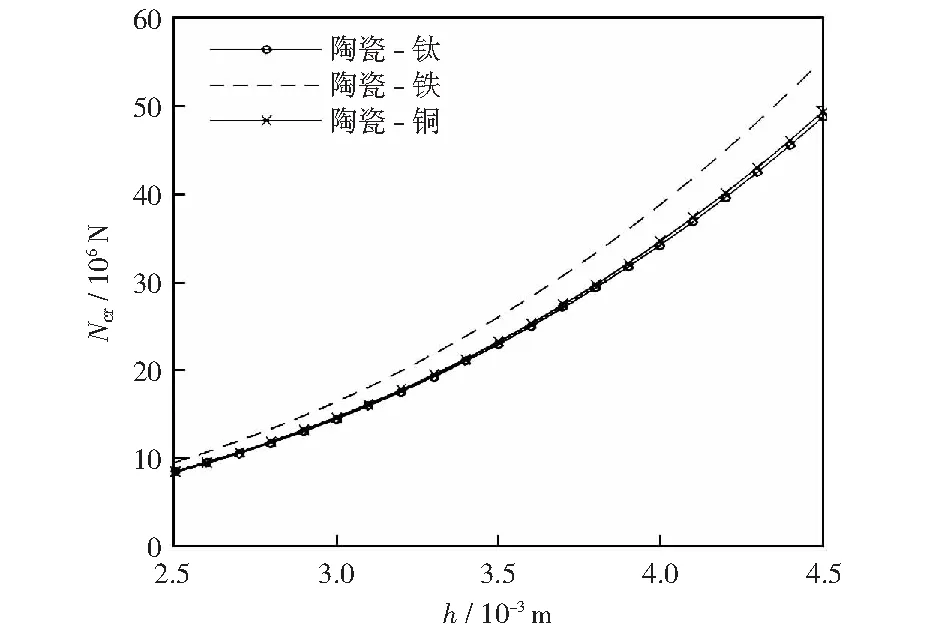
圖7 構成材料不同時臨界載荷與厚度的關系Fig.7 Relationship between critical load and thickness when material is different

圖7是當CFSS功能梯度板的Lcr、Lb、k、m、n相同，構成材料不同時，Ncr與h的關系曲線。由圖可知，圖7表明，Ncr隨h的增大而增大。當h相同時，陶瓷-鐵板的臨界載荷高于陶瓷-鈦板，而陶瓷-鈦板與陶瓷-銅板的臨界載荷曲線幾乎重合，表明材料的彈性模量變化對屈曲臨界載荷的影響較為明顯，泊松比的影響相對較小，與圖2所得結論相符。

圖8是當CFSS功能梯度板的Lb、k、m、n與構成材料相同，Lcr不同時，Ncr和h的關系曲線。當Lcr一定時，Ncr隨h的增大而增大。當h相同時，Ncr隨Lcr的增大而減小，且Ncr降幅隨Lcr的增加呈遞減趨勢，與圖3所得結論相符。

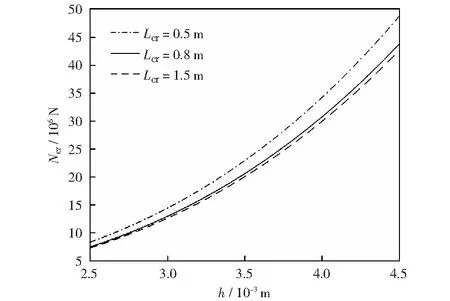
圖8 臨界長度Lcr不同時臨界載荷與厚度的關系Fig.8 Relationship between critical load and thickness when length is different

圖9是當CFSS功能梯度板的Lcr、Lb、m、n與構成材料相同，k不同時，Ncr與h的關系曲線。當h相同時，Ncr隨k的增大而減小，k值越小曲線傾斜度越大，k值在(0，1)的范圍內變化對臨界載荷的影響明顯，與圖4所得結論相符。

圖9 梯度指數k不同時臨界載荷與厚度的關系Fig.9 Relationship between critical load and thickness when gradient index is different

圖10是當CFSS功能梯度板的Lcr、Lb、k、m與構成材料相同，n不同時，Ncr和h的關系曲線。當h相同時，Ncr隨n的增大而增大；n越大，曲線傾斜度越大，相鄰模態數對應的Ncr差值越大。這表明：高階模態對臨界載荷的影響較明顯，低階模態影響較小。

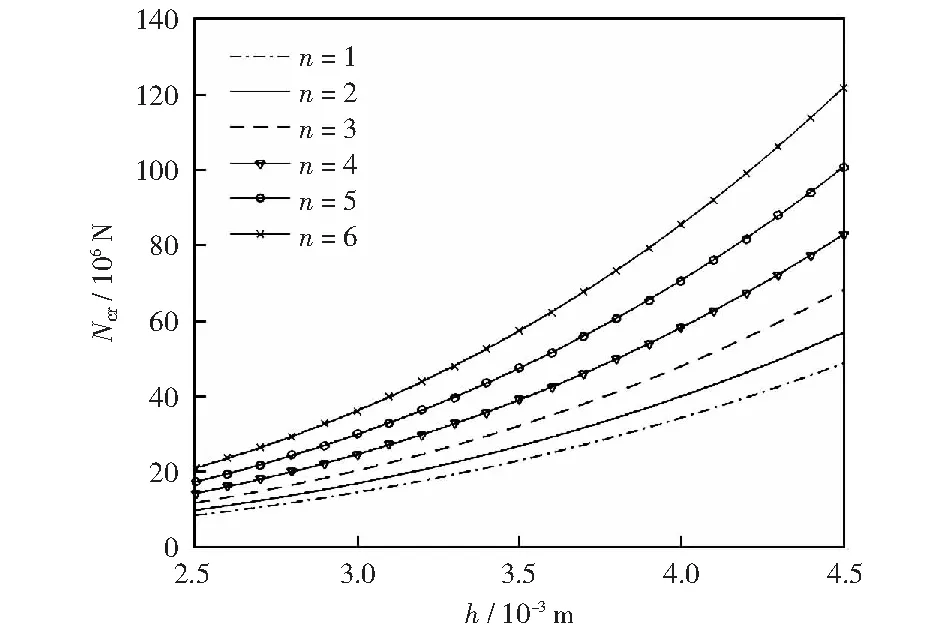
圖10 X方向模態數n不同時臨界載荷與厚度的關系Fig.10 Relationship between critical load and thickness when the modal number of X direction is different

圖11是當CFSS功能梯度板的Lcr、Lb、k、n與構成材料相同，m不同時，Ncr與h的關系曲線。當h相同時，Ncr隨m的增大而增大；并且m越大，相鄰階數對應的Ncr差值越大。結合圖10可知, 當功能梯度板厚度變化時，Y方向模態數比X方向模態數對臨界載荷影響明顯。

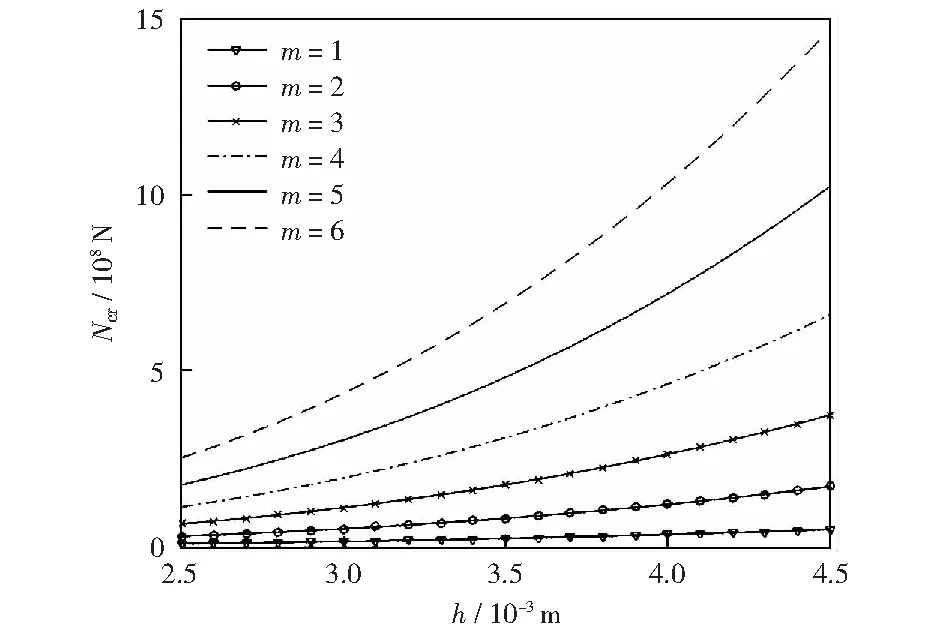
圖11 Y向模態數m不同時臨界載荷與厚度的關系Fig.11 Relationship between critical load and thickness when the modal number of Y direction is different

圖12是當CFSS功能梯度板的幾何尺寸一定時，兩種構成材料的泊松比與動力屈曲臨界載荷的關系圖。

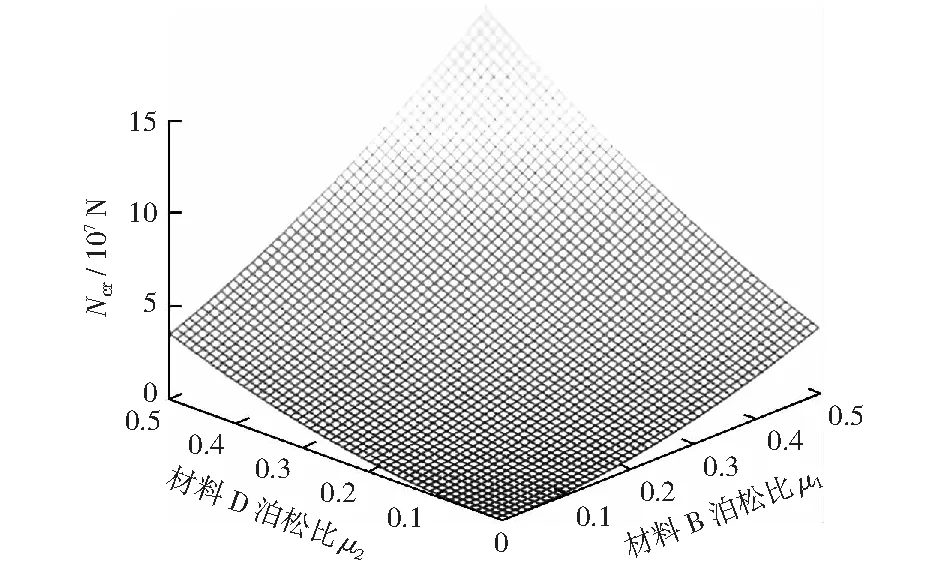
圖12 CFSS板中B、D兩種材料之間的臨界載荷與泊松比μ1，μ2的關系Fig.12 Relationship between critical load and Poisson ratio when CFSS plate is made up of two materials

由圖可知，當功能梯度板的幾何尺寸一定時，臨界載荷隨構成材料的泊松比增大而增大，并且其函數曲線的斜率隨泊松比的增大而增大。

圖13是當CFSS功能梯度板的幾何尺寸一定時，兩種構成材料的彈性模量與板動力屈曲臨界載荷的關系圖。當功能梯度板的幾何尺寸一定時，臨界載荷隨構成材料彈性模量的增大而增大，且變化趨勢接近線性關系。

圖13 CFSS板中B、D兩種材料之間臨界載荷與兩種材料彈性模量E1，E2的關系Fig.13 Relationship between critical load and elastic modulus when CFSS plate is made up of two materials

圖14是當功能梯度板X方向與Y方向模態數取值不同時，功能梯度材料板的屈曲模態圖。

由圖可知，功能梯度板屈曲模態幅值w，隨X方向正向遞增，且固定端屈曲模態幅值較大；隨Y方向正向不變，且屈曲模態呈正對稱或反對稱分布。這表明邊界條件對功能梯度板的屈曲模態影響較大，模態階數越大，雙向屈曲模態越復雜。

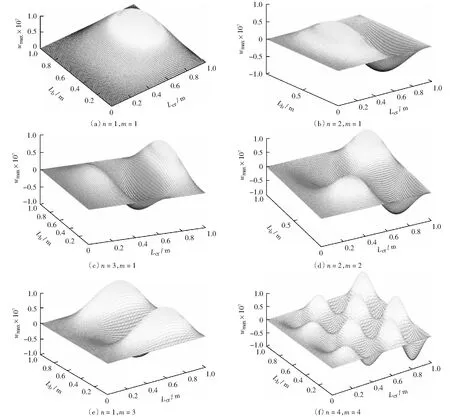
圖14 模態數取值不同時的CFSS功能梯度板屈曲模態圖Fig.14 CFSS buckling mode image of functionally graded material plate when model number are different

5 結論

1) 基于Vogit應變假設與Kirchhoff薄板理論以及線性混合率，由Hamilton原理導出了功能梯度材料板動力屈曲控制方程式(16).

2) 用試函數法與分離變量法求解，得到了功能梯度材料板在相應邊界條件下的動力屈曲臨界載荷的解析表達式(25)和屈曲的模態表達式(26)，其屈曲模態如圖14.

3) 用MATLAB軟件編程計算式(25)和式(26)，討論了功能梯度板的臨界長度、寬度、厚度、梯度指數、材料屬性以及屈曲模態階數對屈曲臨界載荷及屈曲模態的影響。結果表明：功能梯度板動力屈曲臨界載荷隨長度的增大呈指數式下降，隨厚度的增大而增大；屈曲臨界載荷隨梯度指數k的增大而減小，且在(0，1)范圍內變化對臨界載荷影響較大；屈曲臨界載荷隨構成材料的彈性模量、泊松比的增大而增大，且彈性模量影響較大，泊松比影響較小；屈曲臨界載荷隨模態數的增大而增大，當功能梯度板沿Y方向模態數一定時，X方向模態數越大，相鄰階數的臨界載荷差值越大，且不同Y方向模態數的臨界載荷隨長度的增大逐漸趨于水平。當X方向模態數一定時，與上述結論相同；屈曲模態階數越大，雙向屈曲模態越復雜，且屈曲模態變形幅值沿X方向正向遞增，固定端變形較大，表明邊界條件對功能梯度板的屈曲模態影響較大。面內載荷越大，越容易激發功能梯度板產生高階屈曲模態。