基于主成分分析的圖像分割方法

孫前來，王 銀，孫志毅，楊 凱，劉瑞珍

(太原科技大學(xué) 電子信息工程學(xué)院，太原 030024)

圖像分割是機(jī)器視覺中圖像處理的一個(gè)重要和關(guān)鍵的過程，是圖像識(shí)別和圖像理解的基礎(chǔ)。閾值分割是最早的圖像分割方法之一，適用于目標(biāo)和背景有著不同灰度值范圍的圖像。閾值分割具有方法簡單、計(jì)算量小、性能穩(wěn)定等眾多優(yōu)點(diǎn)，因而成為最基本和應(yīng)用最廣泛的圖像分割技術(shù)。圖像的閾值分割主要是根據(jù)圖像的灰度特征，選取一個(gè)或多個(gè)閾值，將圖像中所有像素的灰度值與閾值相比較，把整個(gè)圖像的像素分為兩類或者以上，從而將圖像劃分成背景區(qū)域和一個(gè)或者多個(gè)目標(biāo)區(qū)域。

在圖像分割之前，難以確定圖像中目標(biāo)區(qū)域像素所屬的不同灰度值范圍的數(shù)量，導(dǎo)致難以事先確定圖像分割所需閾值的數(shù)目，這是閾值分割方法的難點(diǎn)之一。此外，閾值的選取適當(dāng)與否會(huì)直接影響圖像分割的精度和圖像描述分析的正確性，所以閾值分割方法的另一個(gè)難點(diǎn)是如何找到合適的閾值將背景像素和目標(biāo)像素分開。當(dāng)圖像中含有多個(gè)分別屬于不同灰度值范圍的待分割目標(biāo)時(shí)，需要多個(gè)閾值才能取得較好的分割效果，然而找到多個(gè)“最優(yōu)”閾值的組合更加困難，需對其進(jìn)行優(yōu)化。早期的閾值優(yōu)化方法多基于窮舉搜索，如最大類間差法(OTSU).但是對于圖像的多閾值分割，利用窮舉搜索的方法尋找“最優(yōu)”閾值組合所消耗的時(shí)間會(huì)隨著期望閾值數(shù)量的增加呈指數(shù)規(guī)律增長。為了提高圖像分割的質(zhì)量或減少圖像分割的時(shí)間消耗，目前大多數(shù)多閾值分割方法采用各種優(yōu)化算法對閾值數(shù)量和閾值大小同時(shí)進(jìn)行優(yōu)化以確定圖像分割 “最優(yōu)”閾值組合，如遺傳算法[1-3]、粒子群算法[4-6]、人工蜂群算法[7-9]及其他優(yōu)化方法[10-13]。采用優(yōu)化算法確定“最優(yōu)”閾值組合，不僅增加了多閾值分割方法的復(fù)雜性，而且對閾值進(jìn)行優(yōu)化時(shí)存在陷入局部最優(yōu)問題的可能。

如果能夠找到一種方法，可以事先確定待分割圖像中背景或目標(biāo)像素的灰度特征，從而避免同時(shí)對閾值數(shù)量和大小進(jìn)行優(yōu)化所帶來的問題，還可以降低圖像分割的難度。本文針對背景相對簡單的一類圖像，提出了一種基于主成分分析(principal component nalysis,PCA)的缺陷分割方法。該方法利用PCA對圖像進(jìn)行線性變換，將原始圖像中背景像素的灰度值變換到重建圖像中的零附近，從而將待分割目標(biāo)分為兩類，相當(dāng)于事先就確定了圖像中背景像素的灰度特征，使得圖像分割較為容易。由于原始圖像中背景像素的灰度值被轉(zhuǎn)換為接近于零，即使圖像中存在多個(gè)具有不同灰度值范圍的待分割區(qū)域，僅使用兩個(gè)閾值就能將目標(biāo)與背景區(qū)分開。

1 主成分分析

PCA就是通過正交變換將一組可能存在相關(guān)性的變量轉(zhuǎn)換為一組線性無關(guān)的變量，目的是去除原始數(shù)據(jù)中向量之間的相關(guān)性，突出原始數(shù)據(jù)中的隱含特征。PCA通常用來減小圖像的尺寸或去除噪聲，是統(tǒng)計(jì)方法中最成功的圖像識(shí)別和壓縮技術(shù)之一[14]。PCA還廣泛應(yīng)用于圖像的去噪、特征提取及融合等領(lǐng)域。實(shí)現(xiàn)主成分分析有兩種基本方法，一種是特征值分解，一種是奇異值分解。可以證明，奇異值分解和特征值分解是等價(jià)的[15]。

本文選擇使用奇異值分解來實(shí)現(xiàn)主成分分析。首先簡要地給出奇異值分解定理。

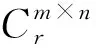
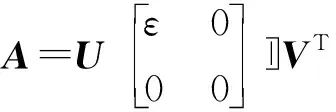
(1)

式中：ε=diag(σ1,σ2,…,σr)；酉矩陣U和V分別為矩陣A的左奇異矩陣和右奇異矩陣。列向量ui(i=1,2,…,m)和vj(j=1,2,…,n)分別稱為矩陣A的奇異值σi的左奇異向量和右奇異向量。

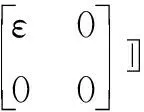
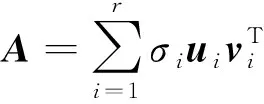
(2)

式中：ui和vi分別為矩陣A的前r個(gè)左右奇異向量。

根據(jù)這一結(jié)論，有理由認(rèn)為相較于較大的奇異值，接近于零的奇異值對應(yīng)的主成分只含有少量矩陣重構(gòu)所需信息，在對矩陣近似重構(gòu)時(shí)也可以忽略。所以，矩陣A可以由下式近似重構(gòu)：

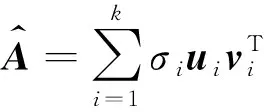
(3)

2 基于PCA的圖像分割方法

針對多閾值圖像分割方法中尋找“最優(yōu)”閾值組合所存在的算法復(fù)雜和時(shí)間開銷較大等問題，本文提出了基于主成分分析的圖像分割方法，可以對背景相對簡單的圖像進(jìn)行分割。

2.1 方法的提出

假設(shè)在理想情況下，圖像背景單一且均勻，待分割目標(biāo)總面積占圖像面積比例較小，而且不考慮噪聲和不均勻光照等的干擾。此時(shí)，圖像的背景就成為了圖像的主要信息，而待分割目標(biāo)是圖像的次要信息。由PCA可知，奇異值越大的主成分含有原始數(shù)據(jù)的信息也就越多；如果利用除第一主成分之外的其它主成分對圖像進(jìn)行重建，那么重建圖像中將主要包含待分割目標(biāo)的信息，有利于圖像的分割。為了減少圖像分割時(shí)的計(jì)算量，利用奇異值累計(jì)貢獻(xiàn)率達(dá)85%時(shí)的前若干主成分對圖像進(jìn)行重建，即

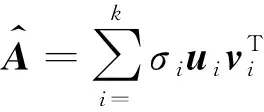
(4)

式中，k為奇異值累計(jì)貢獻(xiàn)率達(dá)到85%時(shí)奇異值的數(shù)量。

圖1(a)為理想情況下的8位灰度圖像，圖中黑點(diǎn)和白點(diǎn)分別用來模擬屬于不同灰度值范圍的待分割目標(biāo)。對圖1(a)進(jìn)行奇異值分解并按照式(4)對圖像重建，利用兩個(gè)閾值對重建圖像進(jìn)行分割，結(jié)果如圖1(b)所示。圖1(c)為理想圖像的灰度統(tǒng)計(jì)直方圖，由圖可知其背景像素的灰度值為128.重建圖像的直方圖如圖1(d)所示。

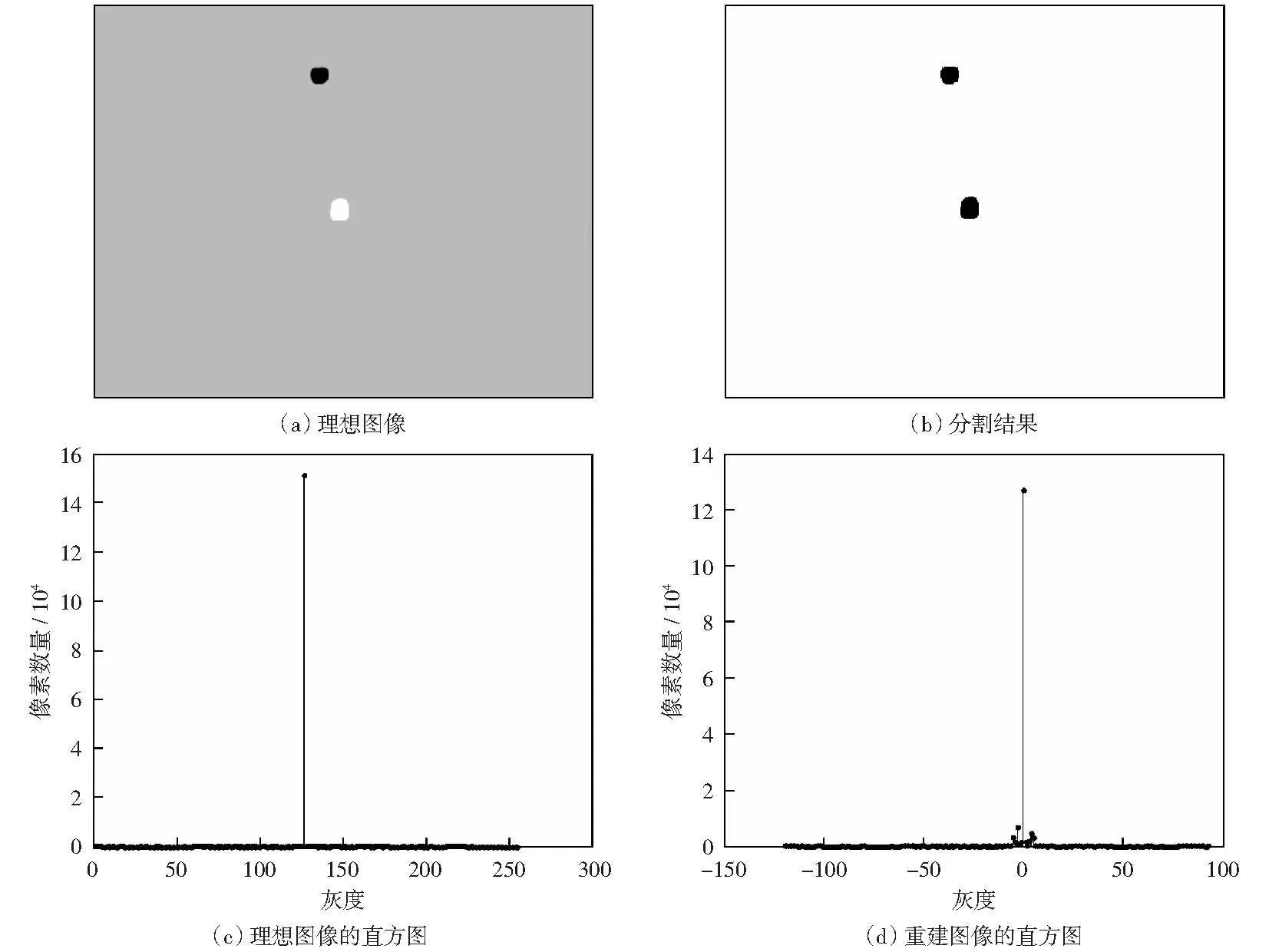
圖1 理想圖像的分割結(jié)果Fig.1 Segmentation of an ideal image

經(jīng)過線性變換后，原始圖像中背景像素的灰度值被變換到重建圖像中零附近。在重建圖像中，“灰度值”可能會(huì)出現(xiàn)小于零的情況，這和原始圖像中灰度值小于背景的像素對應(yīng)；大于零的部分和灰度值大于背景的像素對應(yīng)。此時(shí)，目標(biāo)被分成兩類，一類比背景暗，一類比背景亮，可以利用兩個(gè)位于零附近的閾值在重建圖像中對目標(biāo)進(jìn)行分割。

圖1說明基于PCA的缺陷分割方法在理想情況下是有效的，接下來以實(shí)際情況下的圖像對其有效性進(jìn)行驗(yàn)證。圖2(a)為一張實(shí)際圖像，圖2(b)為分割結(jié)果，圖2(c)和(d)分別為圖像重建前后的直方圖。由圖2可知，經(jīng)圖像重建后，原始圖像中背景像素的灰度值同樣被轉(zhuǎn)換到重建圖像中零附近。

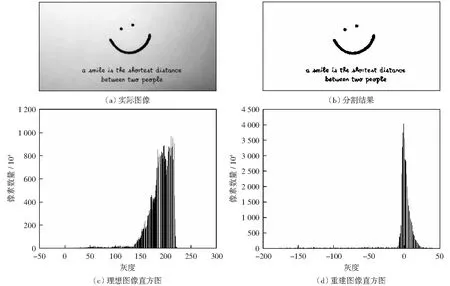
圖2 實(shí)際的分割結(jié)果Fig.2 Segmentation of a real image

2.2 圖像分割的具體步驟

基于主成分分析的圖像分割方法的具體步驟如下：

1) 首先對待分割圖像進(jìn)行灰度化得到灰度矩陣M，對灰度矩陣M進(jìn)行奇異值分解，得到M的左/右奇異矩陣U和V；

2) 計(jì)算奇異值的累計(jì)貢獻(xiàn)率，累計(jì)貢獻(xiàn)率達(dá)到85%時(shí)停止計(jì)算并記下當(dāng)前奇異值的個(gè)數(shù)k；

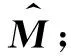
4) 找到合適的閾值T1和T2，且滿足T1>0和T2<0；

5) 利用閾值對圖像進(jìn)行分割，得到二值化的分割結(jié)果。

3 圖像分割實(shí)驗(yàn)

為了驗(yàn)證基于主成分分析的圖像分割方法的有效性，在MATLAB軟件環(huán)境下對圖3(a)所示的實(shí)際圖像進(jìn)行分割實(shí)驗(yàn)，結(jié)果如圖3(b)所示。同時(shí)利用MATLAB自帶的經(jīng)典閾值分割方法OTSU和基于Canny算子的邊緣檢測方法工具箱對圖像進(jìn)行分割，結(jié)果分別如圖3(c)和(d)所示。圖3(a)中除第二張和最后一張之外，其余圖像均來自于以色列威茲曼科學(xué)院的圖像分割數(shù)據(jù)集。

由圖3中大米圖像的分割結(jié)果可知，當(dāng)待分割目標(biāo)在整個(gè)圖像中占比較大時(shí)，本文方法仍能取得較好的分割結(jié)果。如圖3中第二、三圖像的分割結(jié)果所示，當(dāng)圖像中背景和目標(biāo)像素值較為接近時(shí)，基于Canny算子的邊緣檢測算法的分割效果優(yōu)于本文方法和OTSU法，但該方法對紋理較為敏感。OTSU方法只能分割出相對于背景而言或明或暗的一類目標(biāo)。

為了進(jìn)一步驗(yàn)證本文方法在不均勻光照和噪聲等干擾情況下的有效性，以采集于不同的實(shí)際生產(chǎn)環(huán)境、帶有典型缺陷的帶鋼圖像為例，對其表面缺陷進(jìn)行分割實(shí)驗(yàn)， 并與OTSU法和基于Canny算子的邊緣檢測方法進(jìn)行對比，結(jié)果如圖4所示。圖4(a)中，從左到右依次為帶有多個(gè)孔洞、擦痕、輥印、黑斑、銹痕以及單個(gè)孔洞等缺陷的帶鋼圖像。

由帶鋼表面缺陷的分割結(jié)果可知，OTSU法對不均勻的光照較為敏感，導(dǎo)致其存在對缺陷不能有效分割的情況。基于Canny算子的邊緣檢測方法對噪聲和紋理極為敏感，分割結(jié)果將給后續(xù)的缺陷識(shí)別和分類帶來較大困難。

以上實(shí)驗(yàn)結(jié)果驗(yàn)證了基于PCA的圖像分割方法的有效性。圖像分割實(shí)驗(yàn)結(jié)果表明，該方法對噪聲和不均勻的光照均不敏感，分割效果總體上優(yōu)于OTSU法和基于Canny算子的邊緣檢測方法。

圖3 多張實(shí)際圖像的分割結(jié)果Fig.3 Segmentation of some real images

圖4 帶鋼典型缺陷的分割Fig.4 Segmentation of steel strips with typical defects

4 結(jié)論

對于背景較為簡單的一類圖像，基于主成分分析的圖像分割方法可以通過線性變換將圖像中背景像素的灰度值變換到零附近，從而僅利用兩個(gè)零附近的閾值就能夠?qū)D像中處于不同灰度值范圍的目標(biāo)進(jìn)行分割。采集于不同環(huán)境下的圖像的分割實(shí)驗(yàn)驗(yàn)證了該方法的有效性。該方法可以事先確定圖像分割所需閾值數(shù)量，而且只有兩個(gè)閾值的大小需要優(yōu)化，降低了多閾值分割方法中閾值優(yōu)化算法的復(fù)雜性和閾值優(yōu)化所需的時(shí)間開銷。

基于主成分分析的圖像分割方法的局限性在于只適用于背景相對簡單且待分割目標(biāo)面積在整個(gè)圖像中占比相對較小的場合。因此，該方法需要進(jìn)一步改進(jìn)以擴(kuò)大其適用范圍并降低其時(shí)間復(fù)雜度。