量子糾纏與宇宙學弗里德曼方程?

王燦燦

(上海大學物理系,上海 200444)(2018年4月25日收到;2018年5月28日收到修改稿)

1 引 言

在過去的幾十年里,量子理論取得了突飛猛進的發展,特別是量子糾纏,因為時空幾何可以被看作是代表微觀量子態的糾纏結構[1,2].如果兩個粒子的波函數不能寫成它們各個部分的直積,那么它們之間就存在糾纏.如果一個體系存在量子糾纏,那么通過觀察體系中的一部分信息可以了解另一部分的信息.量子糾纏的提出是為了解決許多非局域性物理問題,是量子體系中一種非局域性關聯,通過研究量子糾纏可以了解微觀事物間的新的關聯方式.量子糾纏是可觀測的,其中,糾纏熵是量子信息的測度.糾纏熵是一個比較基礎的物理量:在凝聚態理論中,它用來區分新的拓撲相或不同的臨界點;在量子場理論的背景下,糾纏熵可以作為規范理論中相變的一個有用的探針;此外,它在討論重整化群流的結構中也有新的應用.糾纏熵一直被認為是黑洞熵的起源,而對于糾纏的考慮也引發了一個關于霍金輻射和黑洞蒸發性質的新的討論.糾纏熵在理解時空量子結構中也起著重要作用,以及在反德西特/共形場論(anti-de sitter/conformal field theory,AdS/CFT)對偶理論的討論中也會有糾纏熵的出現.AdS/CFT對偶理論是以弦論為基礎發展起來的,是研究強耦合量子場論比較有潛力的工具,它將規范理論中的強耦合區域與經典引力理論的弱耦合區域聯系了起來.

Ryu和Takayanagi[3?5]提出了一個計算時空幾何直接的工具——糾纏熵.在邊界場理論中選擇一個特定的空間區域V研究了V與其補集ˉV之間的糾纏熵,在共形場論糾纏與雙時空幾何(AdS空間)之間構建了一個定量的聯系[6].最近,Jacobson[7]通過最大真空糾纏假說得出了半經典愛因斯坦方程,該假說認為小測地球的糾纏熵在給定體積下是最大的,在幾何和量子場的一個局部最大對稱真空態中給出了一個定性的論據表明愛因斯坦方程暗示了這個假設的有效性.因此,從最大真空糾纏熵假設出發得到了完整的非線性愛因斯坦方程.在幾何上,測地球半徑的選擇遠小于任何宏觀長度尺度,所以黎曼正則坐標的使用是合理的.Jacobson利用閔可夫斯基時空中變分δgab在黎曼坐標系下計算面積缺陷δA,可得面積缺陷與紫外區的糾纏熵變化δSUV成正比,即δSUV=δA/(4G).總熵變δStotal受到從物質場狀態的變化δ|ψ〉所產生的紅外區δSIR的貢獻,假設小測地球中的真空糾纏熵是極值,總熵變δStotal=δSUV+δSIR就為零,通過進一步利用量子糾纏第一定律δSA=δ〈HA〉,最后可以推導出愛因斯坦方程[7].

本文主要從糾纏的觀點理解宇宙動力學,在糾纏是時空的基本元素的假設下展示了如何從糾纏第一定律得出弗里德曼方程.文中采用費米正則坐標(Fermi normal coordinates,FNC)對面積缺陷進行了擴展討論[8].FNC描述了一個類時測地線并且沿著測地線克里斯托弗符號對有限的空間區域和所有的時間區域是有效的.在宇宙學背景下,FNC只適用于尺度遠小于哈勃視界的情況下,弗里德曼方程首先建立在FNC系統中.然后引入共形費米坐標(conformal Fermi coordinates,CFC)[9],在CFC中主要研究的是空間曲率為零的平坦宇宙,弗里德曼方程將會在CFC中再次被推導出來.

下面對量子糾纏第一定律做一個簡短的回顧.對于一般量子系統中的任意狀態,子系統A的密度矩陣可以描述為這里ρtotal是整個系統的密度矩陣,是A的補集,通過糾纏熵SA描述子系統A與系統其余部分的糾纏.定義馮·諾依曼糾纏熵為

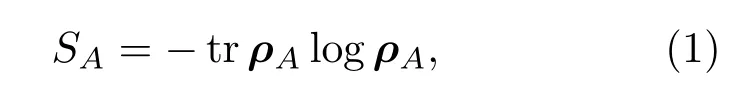
其中ρA為子系統A的密度矩陣,通過哈密頓量定義密度矩陣ρA,

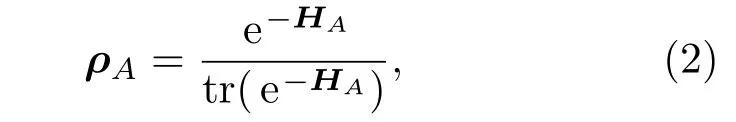
其中,HA是厄米算符,ρA是厄米的且為正,(2)式右邊的分母保證了ρA有單位跡.子系統A的糾纏熵的一階變分為

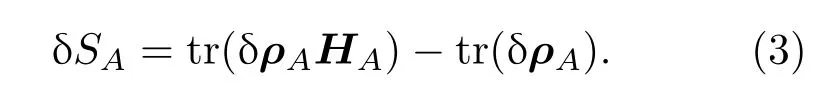
密度矩陣ρA對任何狀態都有單位跡,因此最后一項為零,于是得出量子糾纏第一定律

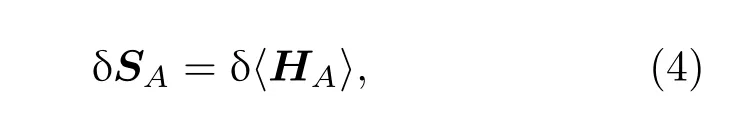
其中哈密頓量HA是根據最初的無擾的密度矩陣定義的.方程(4)被解釋為量子糾纏的第一定律,因為它反映了熱力學第一定律的一般形式[10].從熱狀態ρA=eβH/tr(e?βH)開始,方程(4)就可以簡化為通常的熱力學第一定律δ〈H〉=TδSA.

本文從量子糾纏第一定律出發,結合理想流體的連續性方程,得出宇宙學弗里德曼方程.本文的結構安排如下:第2節簡要回顧了FNC的概念;第3節用FNC計算了面積缺陷;第4節和第5節分別討論了因果結構、糾纏熵變化和弗里德曼方程;第6節通過引入CFC推導出了弗里德曼方程;第7節進行了討論和總結.

2 費米正則坐標的簡要回顧

廣義相對論等效原理認為,在一個引力場下慣性參考系中的物理定律在一個無窮小的實驗室是有效的.根據等效原理,引力場效應與在平直時空中的加速效應是局部不可分辨的,其實熱力學中的物理概念是與觀測者有關的.對于一個平直時空的零溫情況下,一個自由下落觀察者不會感覺到溫度,而加速的局域Rindler觀測者能同時感覺到溫度和觀測到熵.在宇宙學中,時間變量與空間變量不同,其中一個特殊的時間變量是測地線觀測者的固有時間,而空間隨著時間會出現膨脹.在時空中的每一個事件中，時空都是局部平坦的,需要引入黎曼正則坐標,其基本的思想就是用測地線通過一個給定的點定義附近點的坐標.

這里引入FNC[8],然后從幾何角度進行構建.我們考慮一個自由下落觀測者沿著一個世界線移動,時空坐標為正交平行傳播四元組為自由下落觀測者的軌跡是一個類時測地線,是觀測者O的類時單位切向量形成觀測者的局部空間系.通過類空測地線在任意事件Q(τ)正交于世界線可以構造一個局部超曲面.考慮在Q(τ)鄰近的一點P,坐標xμ位于這個超曲面上,從Q(τ)到P將有一個獨特的時空測地線連接,因此,分別定義Q點和P點的FNC 為滿足關系

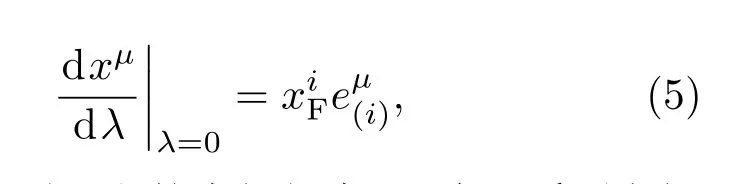
其中λ是從Q到P段的本征長度,因為一系列空間基集是正交的,FNC度規是在O中是成直角的,于是得出

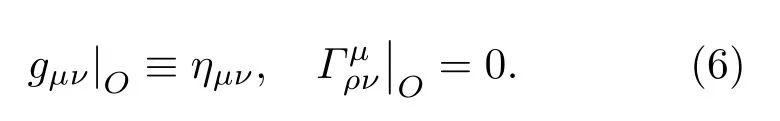
基于以上的研究可以利用xiF逐階計算FNC,重復使用測地線方程來計算,包括一些坐標系(例如史瓦西坐標)xμ和FNC,然后得到任意坐標xμ和FNC之間的關系:

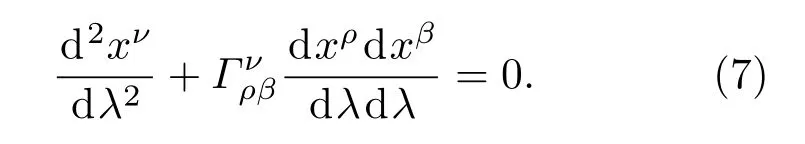
把xμ展開成

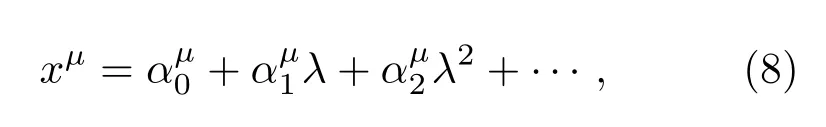
其中

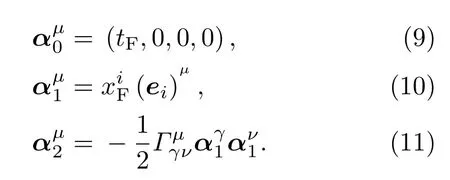
更簡單地說,可以把時空元素展開為gμv=ημv+所以,在FNC下度規為

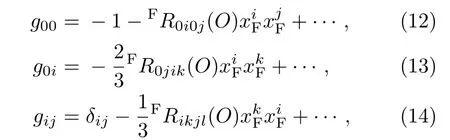
其中FRikjl表示黎曼張量的投影,可以從給定的黎曼張量得出修正.

下面討論FNC中的弗里德曼-勒梅特-羅伯遜-沃爾克(FLRW)度規.

在笛卡爾坐標系中標準的FLRW度規為

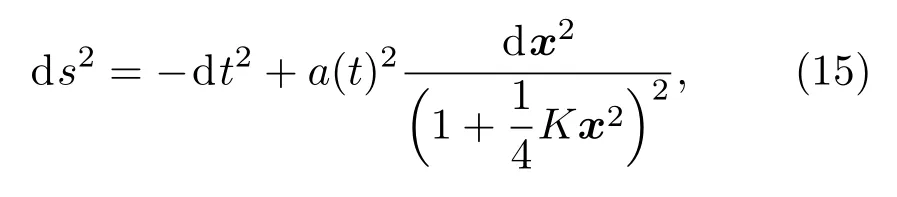
通過下面的度規張量變換得出FNC,

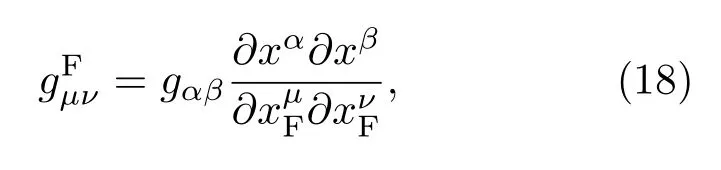
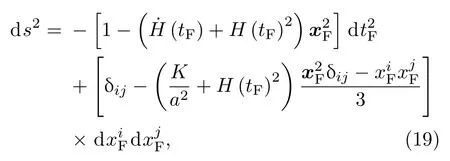
其中H是哈勃常數,這里得到的FNC也可以通過(12)–(14)式求出.特別地,里奇標量的空間分量可以容易寫作

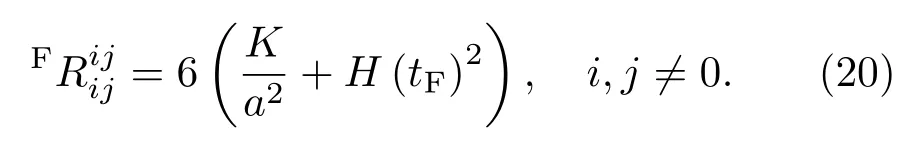
3 面積缺陷

首先,考慮d維時空在測地線中心O的FNC系,測地線從O發出正交于ua,形成一個d?1維類空球.假設l是球的半徑,考慮一個基于O的FNC系,類時坐標類空坐標其中r是測地距離,ni是一個單位向量,滿足δijninj=1,時空度規的號差取為(?+++).假設球的半徑遠小于局部曲率長度(即l?H?1).Σ上空間度規gij在(14)式已經給出,Σ的FNC坐標的二階體積元為

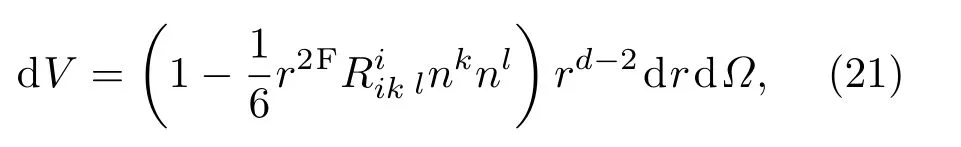
d?代表單位(d?2)球體上的面積微元.對于球對稱函數從到積分

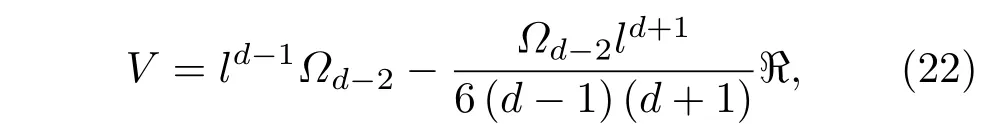
?=的空間里奇標量,?d?2代表(d?2)球體上的面積.利用積分與閔可夫斯基空間在?=0處相比,固定半徑下的體積變化

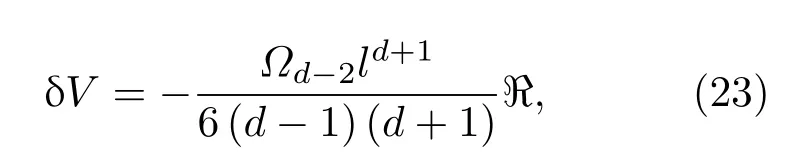
?Σ面積變化由dδV/dl給出,即

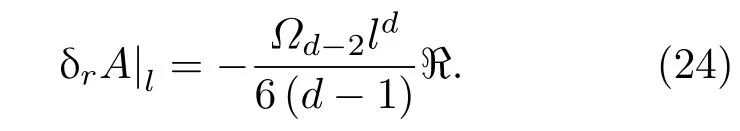
當球的半徑變化時,體積和面積的變化形式為

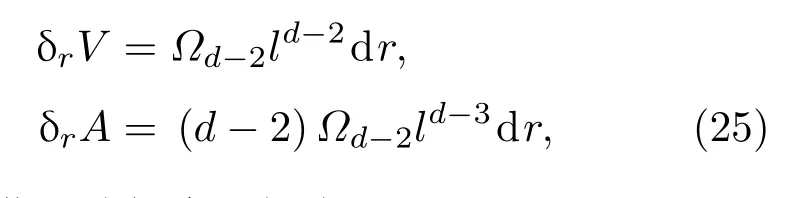
總面積變化可分解為兩部分,

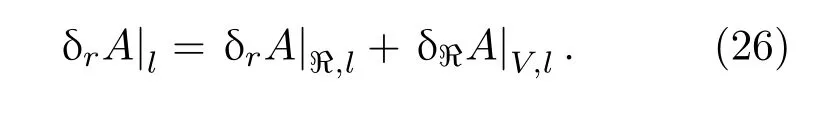
然后在固定體積的面積變化滿足[7]

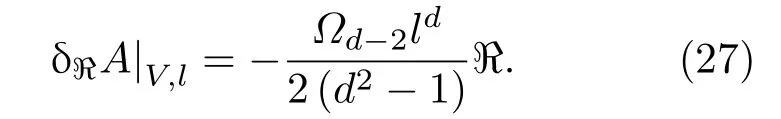
對于FLRW度規,空間里奇標量為?=6(H2+k/a2).在本節中可以發現固定半徑和固定體積下的面積變化,利用費米坐標中里奇標量等于兩倍的一般愛因斯坦張量00分量可以聯系到愛因斯坦方程.在文獻[3]中,作者考慮了體積缺陷并從復雜性/體積對偶出發導出愛因斯坦方程.此外,他們發現宇宙加速膨脹可以理解為由量子復雜性造成的.

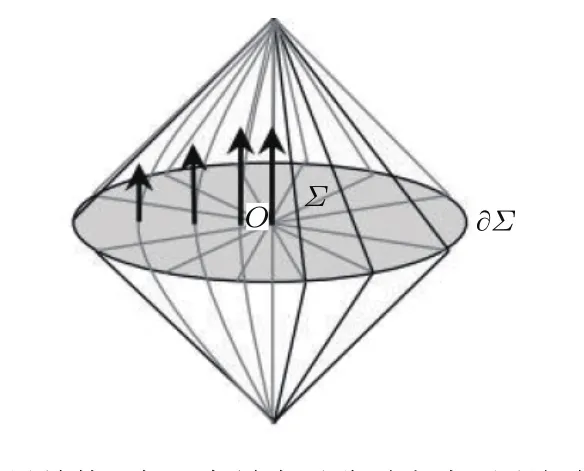
圖1 因果結構,在一個最大對稱時空中,測地球Σ的中心為O,邊界為?ΣFig.1.A sketched diagram for Causal diamond of a ball-shaped Σ region with center O and boundary ?Σ.

4 因果結構

文獻[7]討論了因果結構D(Σ)和閔可夫斯基線元共形等距,由基林(Killing)矢量推導出了獨特的球對稱性因果結構共形等距

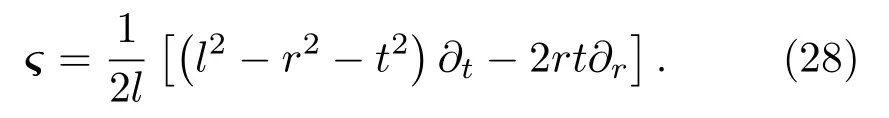
對于FLRW幾何線元ds2=?dt2+a(t)2dx2,可以定義共形時間坐標

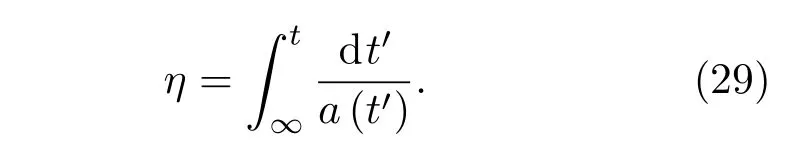
將度規變換為共形閔可夫斯基時空

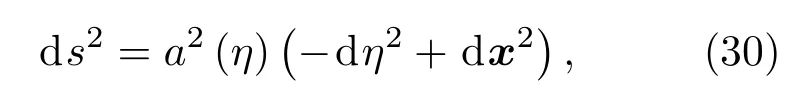
相應的基林矢量為

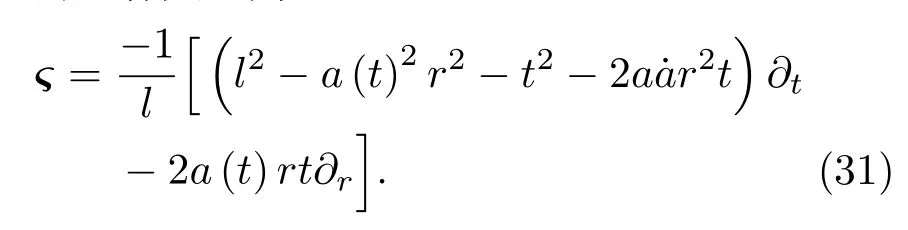
注意當a(t)=1,根據文獻[7]可得相應的基林矢量

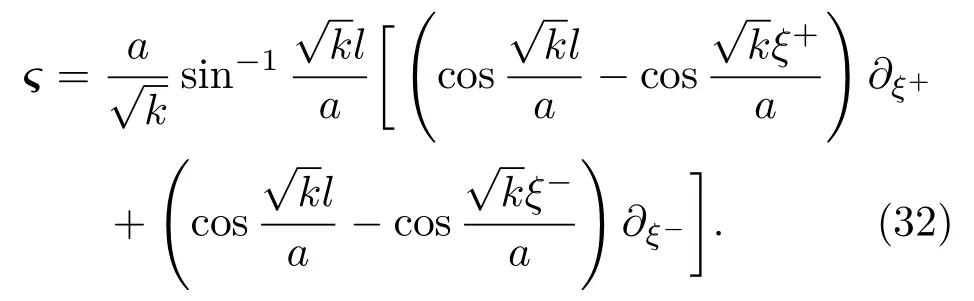
當k=0時基林矢量為

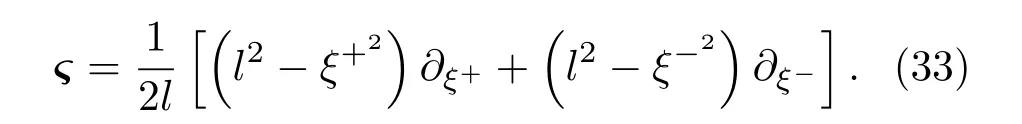
對于一般的在任意的空間曲率FLRW下ds2=度規取為下面的形式:

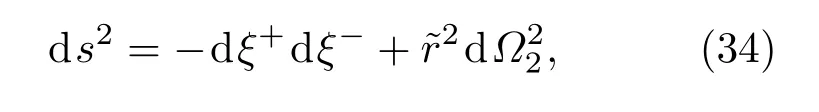
零坐標為

因此,基林矢量采取下面的形式

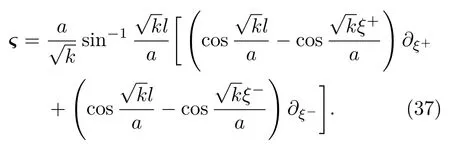
對于非共形物質系統,因果結構D(Σ)糾纏熵由紫外部分與紅外部分組成.如果考慮幾何的變化和量子場的狀態,總熵變可以寫成

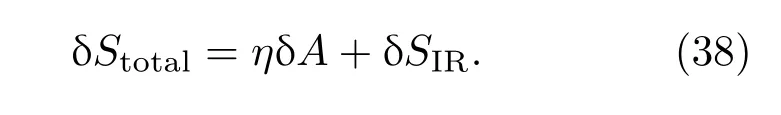
Jacobson在文獻[7]提出最大真空糾纏假說:當幾何和量子場由最大對稱性同時變化時,在固定體積下小測地球中糾纏熵是最大的.由最大真空糾纏假說得

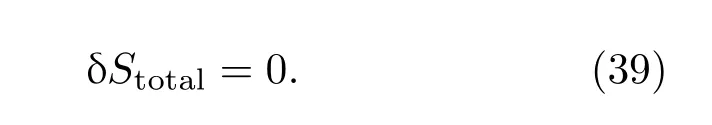
現在繼續在最大真空糾纏假說下推導弗里德曼方程,分別在FNC和FNC系統中.

5 量子糾纏和弗里德曼方程

本節使用糾纏第一定律δSA= δ〈HA〉推導出宇宙學弗里德曼方程.現在假設因果結構封閉的量子態是熱力學平衡的,第3節已經推導出了在固定體積下的面積變化.考慮處于平衡狀態的普通熱力學系統中的最小亥姆霍茲自由能F=E?TS,量子場理論的真空狀態被限制在這個因果結構中可以表示成一個熱密度矩陣:

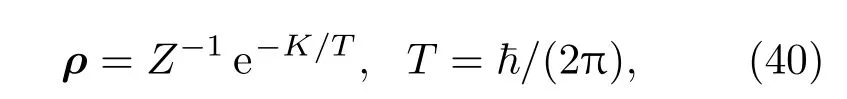
其中K與哈密頓量有關,T是Unruh溫度[11,12],自由能FK= δ〈K〉?TS,δ〈K〉表示模哈密頓量的量子期望值,S=?Trρlnρ代表馮·諾依曼糾纏熵.由最小亥姆霍茲自由能原理知δFK必須為零,于是有

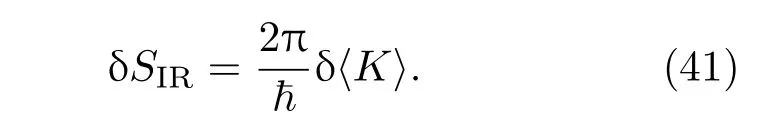
這是對于一個熱狀態的普通的克勞修斯關系,K和H?在文獻[7]中有比較詳細的討論.一般來說,這里的K不是一個局部算子,不生成幾何流,對于普通的FLRW宇宙學,它與CFT無關.對于非共形物質場,文獻[7]猜想中有附加項δX,

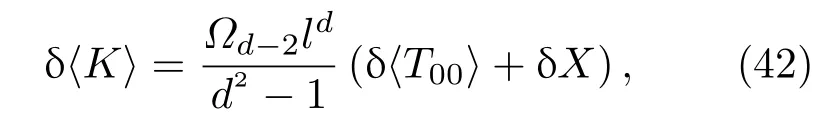
δ〈T00〉是能量密度的變化,δX是一個時空標量,X首次引入于文獻[7],它在量子場理論中是一些標量運算符.下文只考D=4的特殊情況,假設量子場是具有因果關系的,處于熱力學平衡狀態且由真空態支配.在固定的體積下總熵變為0,即從(38),(41),(42)和(27)式可得

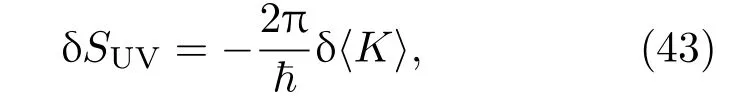
從而

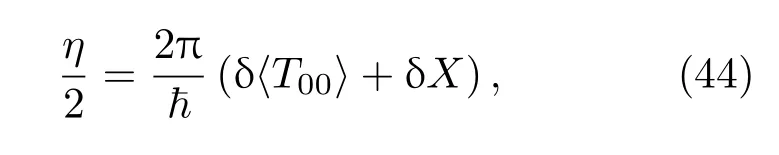
因此

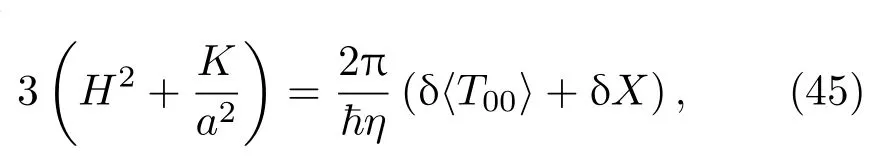
其中η=1/(4πG).下文假設δX=0,對于第一階,假設宇宙不是空的而是由一些物質和能量支配的.這里選擇用理想流體來模擬宇宙中的物質和能量,一個理想流體的能量動量張量可以寫成

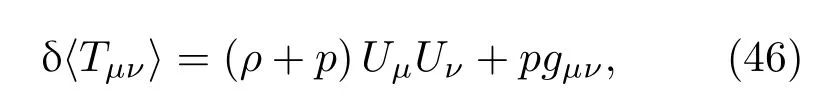
ρ是能量密度,P是壓力,Uμ是流體的四速度,四速度Uμ=(1,0,0,0).能量動量張量可以簡單表示成

方程(45)重新寫為標準的弗里德曼方程

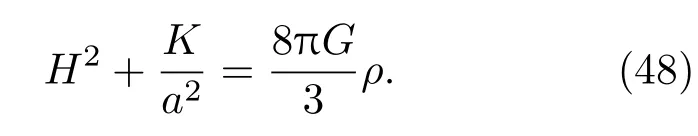
再加上理想流體的連續性方程

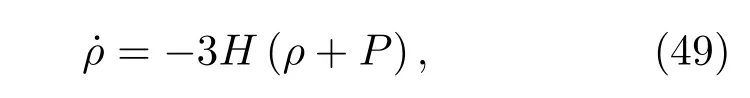
得出另外一個弗里德曼方程

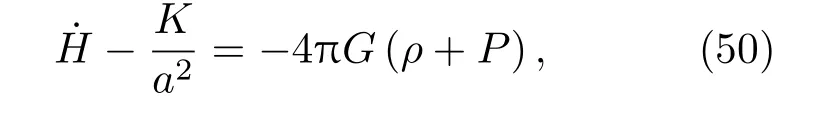
其中,·表示tF的導數.因此,對于FLRW宇宙應用糾纏第一定律得出弗里德曼方程.在這個意義上,弗里德曼方程的出現可以視為是由于物質δ〈HA〉糾纏的變化δSA的原因,推導的有效性僅限于一個小測地球的半徑遠小于視界半徑,為了克服這個局限性,我們將在下一節探討CFC.

6 共形費米坐標(CFC)和弗里德曼方程

現在討論CFC的構建.為了研究宇宙學應用,作者在文獻[9]中引入CFC,CFC在視界外也是有效的.與FNC類似的是它構建在一個類時中心測地線附近,在CFC系中,最低階CFC度規是一個平坦的FLRW時空.度規取為下面的形式:

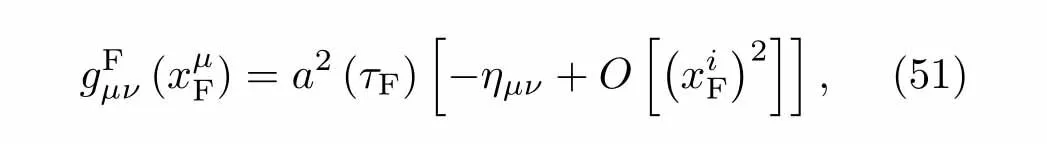
a(τF)代表共形時間,為了計算的方便引入共形度規下面簡要介紹CFC的構建.

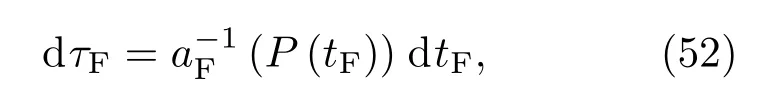
這里τF表示時間坐標,點P有CFC坐標(τF,0).考慮一族與有關的共形測地線通過條件分別得到P點的仿射參數和正切矢量.換句話說,αi通常決定測地線方向,λ測量共形度規測地線距離[9].P點在共形測地線上點的坐標為

于是可得CFC度規與共形黎曼曲率張量之間的關系:

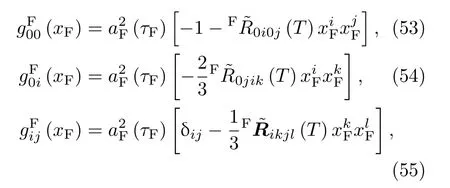
Fikjl是黎曼曲率張量,在CFC系下的黎曼張量可以寫作在全局坐標中可以計算出μναβ的分量.

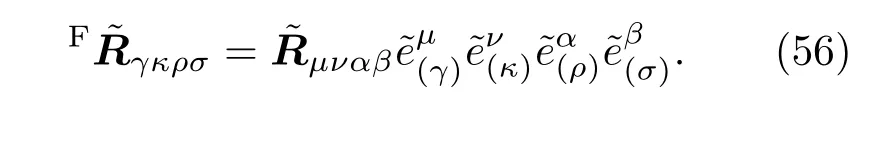
與第3節相似,考慮一個測地球,在真空糾纏熵是極值的條件下δStotal=0.通過類似于第5節的方法,在平坦宇宙中CFC系下弗里德曼方程如下:

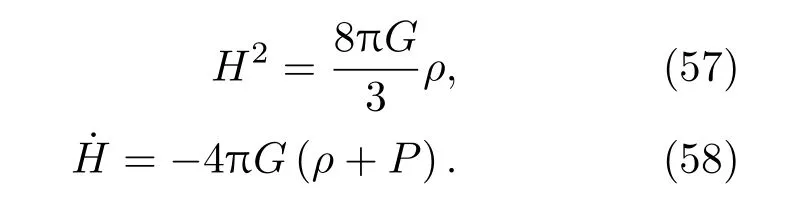
因此,得出FLRW宇宙下的弗里德曼方程在k=0的情況下是有效的.

7 討論與結論

本文探討了量子信息理論的關鍵概念與時空和引力之間的深層聯系,在一個新的坐標系下研究宇宙學,認為時空幾何是微觀量子態的糾纏結構.結合理想流體的連續性方程從量子糾纏第一定律推導出宇宙學弗里德曼方程,討論了時空微觀自由度、糾纏與引力的關系.首先,在FNC下的因果結構尺度l比局部曲率長度小很多,但仍遠遠大于普朗克尺度lp的情況下推導出弗里德曼方程.如果因果結構尺度比得上紫外線尺度lp,那么量子引力效應就變得更強.通過探索CFC系統,我們拓展到一個更大的因果結構尺度進行討論.在這個意義上,可以得到一個曲率修正值較高的引力場方程.

這里介紹的推導過程可以看作是一個弗里德曼方程導出的補充,這從宇宙學表觀視界的熱力學[13?15]可知.而如何從糾纏平衡態獲得高階導數引力下的弗里德曼方程,例如Gauss-Bonnet引力[16?18]和Lovelock引力[14,19],在這兩種引力中,熵與視界面積的關系不再成正比,這時Gauss-Bonnet引力和Lovelock引力中的熵面積關系應該為表觀視界的熵與面積關系.然后重復本文中的推導弗里德曼方程的整個過程,就能得出Gauss-Bonnet引力和Lovelock引力的弗里德曼方程.這可能涉及到糾纏第一定律的擴展,在此不做具體的推導.類似地,通過糾纏第一定律,文獻[20–30]進行了一系列的計算,在均勻標量場的暴漲模型考慮弗里德曼方程將是很有趣的.對于糾纏的本質以及宇宙的評估的研究也會是一個有趣的課題[3].

量子糾纏可以用來描述量子物質態,對量子物質態中糾纏的大小的研究已經成為一個值得探討的問題.而對糾纏結構面積定律的研究也有助于研究張量網絡的算法[31],利用量子體系糾纏熵正比于其邊界的大小為研究量子多體提供了可能.而有研究表明黑洞熵在某些方面也與面積定律有著深刻的聯系[32].另外,從量子信息的角度來審視引力可以進一步促進我們對時空的本源的理解,從而更進一步地了解宇宙學.所以,量子糾纏的深遠影響到底是什么,還需要我們去挖掘其中的奧秘.