錨護網絡結構多目標進化優化設計方法研究

張玉攀

（同煤集團燕子山礦技術科，山西 大同 037300）

煤礦開采巷道采用錨桿支護，其支護結構的優良直接關系到巷道的穩定性，采用錨桿數量越多，巷道支護越穩定，但隨之而來的是支護時間和成本的增長，對煤礦開采的高效率形成了牽制[1-2]。相反，錨桿數量少雖然可以減少支護成本，但其支護穩定性可能會受到影響，出現冒頂、片幫和坍塌事故更是損失嚴重[3-4]。所以對于煤礦巷道的支護應選擇合理的巷道支護結構，在保證安全的基礎上盡可能的節省成本。本文采用多目標進化優化設計方法對巷道錨護進行了研究，圍繞支護質量、成本和時間進行優化分析，以實現巷道錨護的最優方案選取。

1 錨護網絡構架多目標數學模型

1.1 決策變量

在錨護網絡設計過程中，要盡可能的考慮安全、成本和效率三方面問題，本文將以支護質量、成本和時間三個目標為函數來進行分析，需要建立三目標優化模型，并通過數學算法進行模型分析[5]。支護質量和支護網絡關系復雜，因此將圍巖變形量作為分析支護質量的參考量，其包含頂底板和幫部移近量，創建模型對支護質量進行反映[6]。綜合考慮煤礦巷道支護時間狀況，以錨桿配合錨索組合支護為研究，將支護影響要素作為決策變量，主要包含支護核心參數，設決策變量為x={x1,x2......,xn}，其中參數分別為錨桿直徑、錨桿長度、錨索布置形式、錨索的直徑、錨索和錨桿的排距比值、錨桿頂部間距、錨桿的排距、錨桿幫部間距、錨索的長度、錨桿的預緊力和錨索的預緊力，其中錨索布置形式包括每排布置一根，奇數排兩根，偶數排一根，每排兩根錨索，分別用數字1、2、3代表，排距比值可選0、1、2、3、4、5，其中0表示沒有錨索支護。

1.2 目標函數

支護質量是首先考慮的目標之一，其體現了圍巖在錨護網絡的支護下的可靠程度，可依靠圍巖變形情況來反映支護質量，將頂底板和兩幫的移近量進行測量來表示圍巖的變形情況，因其具有高度非線性關系，所以采用代理模型評價錨護方案與支護質量的聯系。因為錨桿和錨索大量參數為離散數據，所以通過正交實驗得出方案來確保數據典型,運用監督學習方法來識別支護方案與頂底板、兩幫移近量的聯系，設計頂底板和兩幫支護質量代理模型分別為：RF（x）和TS（x）。

支護成本是在維持支護穩定的基礎上主要研究的方向，影響著開采的經濟性，錨桿錨索的材料、重量都是支護成本的主要因素，因為支護所用錨桿及錨索的材料相對比較單一，所以支護成本通過支護所需材料的重量來進行衡量，支護成本可用以下公式計算：

式中：

cg-錨桿價格，元/kg；

cs-錨索價格，元/kg；

ρg-錨桿密度；

ρs-錨索密度；

kd-頂板布置的錨桿寬度，m；

kc-兩幫布置的錨桿寬度，m；

L-巷道長度，m。

支護時間體現了開采的總體速度，對生產效益影響重大，支護時間受支護材料的總體積影響，可以通過以下公式計算支護時間：

式中：

tg-錨桿支護時間，min/m3；

ts-錨索支護時間，min/m3。

根據巷道工程要求，確定目標函數極限值作為約束條件，設計錨護網絡多目標優化模型，因為函數公式為：

選擇隨機100組支護成本與時間的數據聯系進行分析，如圖1所示。

由圖1可以看出支護時間和成本存在擬合線性關系，C(x)=aT（x）+b，由此可將支護時間的求解簡化為支護成本的求解，目標函數可簡化為：

2 實例分析

本文以同煤集團燕子山礦西區5#層8405工作面為研究對象，運用FLAC3D以及MATLAB軟件進行計算，使用設計方法為非支配排序的多目標遺傳算法，種群規模為200，最大迭代次數為300，交叉指數20，變異指數20，兩者概率為0.8和0.2。優化計算后結果如圖2所示。

圖2 錨護網絡結構優化方案

由圖2可以看出，優化后方案并不僅有一個，存在三個方案，分別是：最小幫部位移量、最小頂底板位移量和最小支護成本，參考其他文獻最優方案[4]，設為第四種方案，分別對四個方案進行結構分析，得出錨護網絡斷面分布如圖3所示，頂底板位移量和兩幫位移量如圖4、圖5所示。

圖3 錨護網絡斷面分布

圖4 巷道頂板和底板位移量

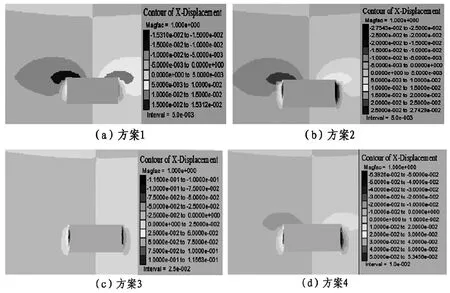
圖5 巷道兩幫位移量

由以上分析結果可以得出，巷道頂底板和幫部移近量低于已經存在的第四種最優方案，說明支護質量優于現有方案，成本最優的方案支護質量也要高于現存支護方案，所以采用這種多目標遺傳算法得到的三個最優方案均能夠滿足設計的要求，是實現更多選擇的優化設計方案。

3 結論

針對煤礦巷道支護過程中存在的錨護網絡結構復雜等問題，考慮安全、經濟和效率等要素的影響，對錨護網絡的支護質量、成本和時間三個目標建立了函數模型，運用非支配排序的多目標遺傳算法進行求解，得出了針對頂底板移近量、兩幫移近量和支護成本的三個最優方案，并與已有優化方案進行模擬對比，結果證明此方法得出的優化結果效果更好，為錨護網絡優化研究提供了理論依據。