DCM—PCCM二次型Boost變換器的分?jǐn)?shù)階建模與分析
譚程 丁祝順 滑藝 賈楠
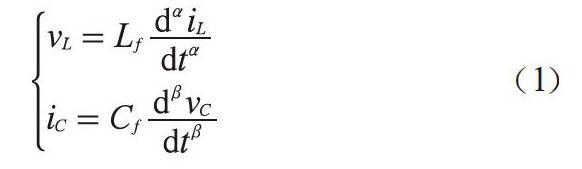

摘 要:文中基于電感和電容本質(zhì)上是分?jǐn)?shù)階的事實(shí),采用分?jǐn)?shù)階微積分理論,建立了類型Ⅰ和類型Ⅱ斷續(xù)導(dǎo)電模式(DCM)-偽連續(xù)導(dǎo)電模式(PCCM)分?jǐn)?shù)階二次型Boost變換器的四階數(shù)學(xué)模型,并對系統(tǒng)進(jìn)行了理論分析,通過數(shù)值與電路仿真,驗(yàn)證了分?jǐn)?shù)階階數(shù)對DCM-PCCM二次型Boost變換器性能的影響,證實(shí)了理論分析的正確性。
關(guān)鍵詞:分?jǐn)?shù)階;二次型;Boost;變換器;DCM-PCCM;電路仿真
中圖分類號:TP39;TM46 文獻(xiàn)標(biāo)識碼:A 文章編號:2095-1302(2018)07-00-04
0 引 言
二次型Boost變換器僅使用了一個功率開關(guān)管就實(shí)現(xiàn)了傳統(tǒng)Boost變換器的級聯(lián),在減少功率開關(guān)管數(shù)量的同時,變換器輸入電壓的范圍得到了拓寬,升壓比得到了提升[1]。因而在新能源領(lǐng)域得到了廣泛應(yīng)用[2,3]。然而,當(dāng)二次型Boost變換器工作在CCM-CCM時,其控制輸出傳遞函數(shù)中存在的三個右半平面(RHP)零點(diǎn)和兩個諧振峰值點(diǎn)不僅加大了控制環(huán)路補(bǔ)償器的設(shè)計難度[4],還嚴(yán)重影響了其對負(fù)載變化的瞬態(tài)性能[5]。PCCM二次型Boost變換器的提出,徹底改善了二次型Boost變換器的缺點(diǎn)[6-8],但目前對PCCM二次型Boost變換器的研究僅建立在整數(shù)階模型基礎(chǔ)上[5,8],并未考慮電感和電容本質(zhì)是分?jǐn)?shù)階對系統(tǒng)帶來的影響[9-11],因此建立一個精確的模型是對PCCM二次型Boost變換器分析與設(shè)計的基礎(chǔ)。目前,隨著分?jǐn)?shù)階微積分理論的不斷發(fā)展以及對真實(shí)系統(tǒng)物理現(xiàn)象認(rèn)知的不斷提高,分?jǐn)?shù)階微積分理論在自然科學(xué)和工程技術(shù)中各學(xué)科領(lǐng)域受到廣泛的研究與應(yīng)用[9,10]。相比于傳統(tǒng)的整數(shù)階數(shù)學(xué)模型,分?jǐn)?shù)階數(shù)學(xué)模型能夠更好地刻畫該物理系統(tǒng)的內(nèi)在本質(zhì)及其演變過程。
本文以PCCM二次型Boost變換器為研究對象,建立了類型Ⅰ和類型Ⅱ DCM-PCCM二次型Boost變換器的分?jǐn)?shù)階數(shù)學(xué)模型,通過數(shù)值與電路仿真驗(yàn)證了分?jǐn)?shù)階階數(shù)對DCM-PCCM二次型Boost變換器性能的影響,證實(shí)了理論的正確性。
1 DCM-PCCM二次型Boost變換器分?jǐn)?shù)階模型的建立
對于分?jǐn)?shù)階電感和電容有如下表達(dá)式:
一個開關(guān)周期T內(nèi),DCM-PCCM二次型變換器有四種工作模態(tài),其電路原理如圖1所示,工作波形如圖2所示。
根據(jù)DCM-PCCM二次型Boost變換器的工作原理以及分?jǐn)?shù)階電感和分?jǐn)?shù)階電容電流和電壓之間的關(guān)系,可得系統(tǒng)的狀態(tài)空間方程為:
其中,IL1為流經(jīng)電感L1的電流,IL2為流經(jīng)電感L2的電流,VC1為電容C1兩端的電壓,VC2為電容C2兩端的電壓,D2和D3為占空比,R為負(fù)載電阻,k1和k2為給定常數(shù),對于類型Ⅰ:k1=1,k2=0;對于類型Ⅱ:k1=0,k2=1。
2 理論分析
根據(jù)Caputo分?jǐn)?shù)階微積分的性質(zhì),可知任意常數(shù)的Caputo分?jǐn)?shù)階微分等于零[10],則式(2)等號左側(cè)等于零,可得分?jǐn)?shù)階DCM-PCCM二次型Boost變換器穩(wěn)態(tài)工作點(diǎn)的表達(dá)式為:
由式(3)可知,分?jǐn)?shù)階DCM-PCCM二次型Boost變換器的升壓比為:
基于系統(tǒng)的工作原理,可得輸入電感L1和儲能電感L2電流紋波ΔiL1和ΔiL2的表達(dá)式分別為:
其中,Γ為伽馬函數(shù)[11]。可知,輸入電感L1的電流紋波ΔIL1不僅與電感值L1、輸入電壓的直流分量Vin、占空比的直流分量D1及開關(guān)管的工作周期T有關(guān),還與輸入電感L1分?jǐn)?shù)階階數(shù)α1有關(guān);且當(dāng)輸入電感L1和儲能電感L2分?jǐn)?shù)階階數(shù)α1=α2=1時,式(5)與用其整數(shù)階模型描述所得結(jié)果相
一致。
對于分?jǐn)?shù)階DCM-PCCM二次型Boost變換器,因其輸入電感電流iL1的初始值為零,根據(jù)式(5),可得輸入電感電流IL1的表達(dá)式為:
基于式(3)和式(5),可得占空比D2和D3的表達(dá)式為:
其中,a=(L1α1Γ(α1)(D1+D2+k1D3))/(R(D2+k1D3)(D1T)α1)。對于類型I:占空比D2和D3均與輸入電感L1分?jǐn)?shù)階階數(shù)α1有關(guān);對于類型II:占空比D2與輸入電感L1分?jǐn)?shù)階階數(shù)α1無關(guān),而占空比D3與輸入電感L1分?jǐn)?shù)階階數(shù)α1有關(guān)。根據(jù)式(3),
(4),(6)和(7),可知升壓比M、輸入電感電流IL1和儲能電感電流IL2、電容電壓VC1和VC2與輸入電感L1分?jǐn)?shù)階階數(shù)α1有關(guān),儲能電感電流紋波ΔIL2與輸入電感L1分?jǐn)?shù)階階數(shù)α1和儲能電感L2分?jǐn)?shù)階階數(shù)α2有關(guān),且當(dāng)輸入電感L1和儲能電感L2分?jǐn)?shù)階階數(shù)α1=α2=1時,其相應(yīng)表達(dá)式與用其整數(shù)階模型描述所得結(jié)果相一致。
如圖2所示,對于分?jǐn)?shù)階DCM-PCCM二次型Boost變換器,需滿足:
根據(jù)圖2可知,分?jǐn)?shù)階類型Ⅰ和類型ⅡDCM-PCCM二次型Boost變換器的臨界狀態(tài)是D3=0且D4≠0,因此,基于式(7),可得其臨界狀態(tài)表達(dá)式為:
由式(9)和(10)可知,輸入電感L1的臨界值及類型Ⅰ和類型Ⅱ之間的臨界值L12均與輸入電感L1分?jǐn)?shù)階階數(shù)α1有關(guān),儲能電感L2的臨界值與儲能電感L2分?jǐn)?shù)階階數(shù)α2有關(guān),且當(dāng)輸入電感L1和儲能電感L2分?jǐn)?shù)階階數(shù)α1=α2=1時,其相應(yīng)表達(dá)式與用其整數(shù)階模型描述所得結(jié)果一致。
3 仿真研究
3.1 DCM-PCCM工作區(qū)域
選取電路的參數(shù)為vin=24 V,d1=0.2,d2=0.1,R=1 000 Ω,f=50 kHz,α1=α2=β1=β2=0.8,C1=C2=100 μF。根據(jù)式(9)和(10),可得分?jǐn)?shù)階DCM-PCCM二次型Boost變換器的工作區(qū)域如圖3所示。因此,為確保分?jǐn)?shù)階二次型Boost變換器工作在類型Ⅰ和類型ⅡDCM-PCCM,選取輸入電感值和儲能電感值分別為L1Ⅰ=5 μH,L2Ⅰ=2 mH和L1Ⅱ=120 μH,L2Ⅱ=2 mH。
當(dāng)系統(tǒng)工作于DCM-PCCM時,如圖4(a)所示,其輸入電感L1的臨界值和L12的臨界值隨其階數(shù)α1的增加而變小;根據(jù)圖4(b)可知,類型Ⅰ DCM-PCCM、類型ⅡDCM-PCCM和DCM-PCCM的工作區(qū)域隨階數(shù)α1的增加而變小;儲能電感L2的臨界值隨α2的增加而變小,如圖4(c)所示;類型ⅠDCM-PCCM、類型ⅡDCM-PCCM和DCM-PCCM的工作區(qū)域隨階數(shù)α2的增加而變大,如圖4(d)所示。
3.2 仿真驗(yàn)證
由于電感和電容本質(zhì)上是分?jǐn)?shù)階的,但目前無法準(zhǔn)確得到從市場上購買實(shí)際電感和電容的階數(shù),且在仿真軟件中也無法找到分?jǐn)?shù)階電感和電容的模型元件。因此根據(jù)分抗鏈結(jié)構(gòu)和改進(jìn)的Oustaloup近似算法,采用圖5和圖6所示分?jǐn)?shù)階電感和分?jǐn)?shù)階電容的等效近似電路模型[9-12]搭建二次型Boost變換器電路模型來驗(yàn)證上述理論分析的正確性。
以類型ⅡDCM-PCCM二次型Boost變換器為例進(jìn)行分析。當(dāng)其他參數(shù)固定時,隨著階數(shù)α1的增加,二次型Boost變換器工作區(qū)域從類型ⅠDCM-PCCM變到類型ⅡDCM-PCCM,如圖7所示。根據(jù)圖7(a)可知,處于類型ⅠDCM-PCCM時,占空比D2隨著階數(shù)α1的增加而增加,占空比D3隨著階數(shù)α1的增加而減少,而在類型ⅡDCM-PCCM時,占空比D2不隨階數(shù)α1的變化而變化,占空比D3隨著階數(shù)α1的增加而增加;根據(jù)圖7(b),(c)和(d)可知,類型Ⅰ和類型ⅡDCM-PCCM工作時,升壓比M、輸入電感電流IL1、儲能電感電流IL2及電容電壓VC1和VC2隨階數(shù)α1的增加而減少。
圖8(a)~(d)分別為分?jǐn)?shù)階和整數(shù)階電路模型輸出電壓VC1和VC2的開環(huán)響應(yīng)曲線,易知DCM-PCCM Boost變換器分?jǐn)?shù)階模型的動態(tài)特性明顯優(yōu)于其整數(shù)階模型,且與整數(shù)階模型相比,分?jǐn)?shù)階模型在相同占空比D1的條件下,具有更高的輸出電壓VC1和VC2。因此,以上分析對分?jǐn)?shù)階DCM-PCCM二次型Boost變換器在今后的實(shí)際應(yīng)用設(shè)計中具有較好的指導(dǎo)作用。
4 結(jié) 語
本文基于分?jǐn)?shù)階微積分理論,建立了分?jǐn)?shù)階DCM-PCCM二次型Boost變換器的數(shù)學(xué)模型,并對分?jǐn)?shù)階系統(tǒng)的穩(wěn)態(tài)和動態(tài)特性進(jìn)行了分析與仿真驗(yàn)證。DCM-PCCM工作區(qū)域與輸入電感L1階數(shù)α1和儲能電感階數(shù)α2有關(guān),當(dāng)其他參數(shù)固定時,類型ⅠDCM-PCCM、類型ⅡDCM-PCCM及DCM-PCCM的工作區(qū)域隨階數(shù)α1的增加而變小,隨階數(shù)α2的增加而變大。在類型ⅠDCM-PCCM工作區(qū)域時,占空比D2隨階數(shù)α1的增加而增加,占空比D3隨階數(shù)α1的增加而減少;然而,在類型ⅡDCM-PCCM工作區(qū)域時,占空比D2不隨階數(shù)的變化而變化,占空比D3隨階數(shù)α1的增加而增加。在類型ⅠDCM-PCCM和類型ⅡDCM-PCCM工作區(qū)域時,升壓比M、輸入電感電流IL1、儲能電感電流IL2及電容電壓VC1和VC2隨階數(shù)α1的增加而降低,且DCM-PCCM二次型Boost變換器的分?jǐn)?shù)階電路模型的動態(tài)特性明顯優(yōu)于其整數(shù)階模型。綜上可知,儲能元器件的階數(shù)對DCM-PCCM二次型Boost變換器有著極其重要的影響,所建立系統(tǒng)的分?jǐn)?shù)階模型能夠真實(shí)反映DCM-PCCM二次型Boost變換器的動力學(xué)特性。
參考文獻(xiàn)
[1]丁明,王偉勝,王秀麗,等.大規(guī)模光伏發(fā)電對電力系統(tǒng)影響綜述[J].中國電機(jī)工程學(xué)報,2014,34(1):2-14.
[2]蘇劍,周莉梅,李蕊.分布式光伏發(fā)電并網(wǎng)的成本/效益分析[J].中國電機(jī)工程學(xué)報,2013,33(34):50-56.
[3]楊平,許建平,何圣仲,等.電流控制二次型Boost變換器的動力學(xué)研究[J].物理學(xué)報,2013,62(16):160501.
[4]李楊,薛花,張宇華,等. 基于大功率模塊化多電平并網(wǎng)變流器的永磁直驅(qū)風(fēng)力發(fā)電系統(tǒng)矢量控制方法研究[J]. 導(dǎo)航與控制,2015,14(4):37-44.
[5]舒立三.偽連續(xù)導(dǎo)電模式二次型Boost變換器研究[D].成都:西南交通大學(xué),2014.
[6] CAO T Q,YOU F,ZHANG F,et al.DSP-Based control of Tri-state Boost PFC converter with high input power factor for wide range of load variations[J]. Journal of Circuits systems and Computers,2015,24(5):2187.
[7]張斐,許建平,楊平,等.偽連續(xù)導(dǎo)電模式Boost PFC變換器研究[J].電子科技大學(xué)學(xué)報,2013,42(5):705-710.
[8]舒立三,許建平,楊平,等.三態(tài)偽連續(xù)導(dǎo)電模式二次型Boost變換器研究[J].電工電能新技術(shù),2015,34(1):7-11.
[9]譚程,梁志珊.電感電流偽連續(xù)模式下Boost變換器的分?jǐn)?shù)階建模與分析[J].物理學(xué)報,2014,63(7):2-10.
[10]譚程,梁志珊,張舉丘.電感電流偽連續(xù)模式下分?jǐn)?shù)階Boost變換器的非線性控制[J].物理學(xué)報,2014,63(20):85-90.
[11] TAN C,LIANG Z S.Modeling and performance analysis of the fractional order quadratic Boost converter in discontinuous conduction mode-continuous conduction mode [C]. Proceedings of IEEE conference on industrial electronics and applications,New Zealand,Auckland,2015.

