基于市場需求下共享單車分配與調度運營方案
朱 闖 高嘉悅 吳海霞 趙 璽
石家莊鐵道大學,河北石家莊 050043
共享單車作為全新的經濟共享模式和全新的公共交通方式,有效地解決了城市“最后一公里”的問題,深受廣大市民的喜愛。然而通過調查,共享單車公司在爭搶市場的同時造成了大量的資源浪費,引發了許多問題, 給社會治理帶來了新的挑戰。在參考公共自行車交通的基礎上,根據相關數據計算出南京市共享單車需求量,進而合理優化共享單車的分配與調度才能避免資源浪費。解決了分配與調度問題后,將其分析結果運用到企業經營上,在代入數據計算過程中探究經營方案合理性。
1 背景
共享單車的出現極大地方便了人們的出行,但現實生活中出現的極多狀況,例如,公民不合理地停放共享單車,會導致下一個使用者不能及時使用單車,嚴重的,還會妨礙到交通。因此,合理地分析共享單車的市場需求,制定合理的單車投放方案,才能保證共享單車的均衡發展,同時也盡可能減少給交通帶來的負面影響。由于各個城市的發展、人口數量、區域面積以及地形等因素的影響,我們就中國一典型城市(南京)進行分析和研究。
2 分析過程
2.1 需求量的分析
共享單車的需求量與很多因素有關,我們選取人口數量、輻射區域 、通勤市場為指標,對共享單車資源需求量進行分析。
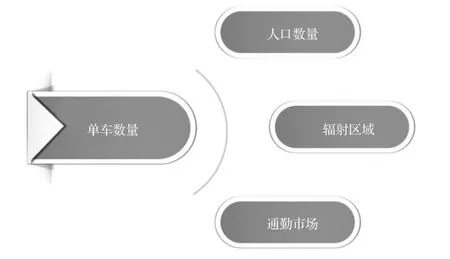
圖1 共享單車需求量指標示意圖
建立最簡單的計算模型:Mi=PL;式中:Mi代表共享單車需求量;P代表人口數量;L代表單車市場滲透率。
不同年齡段、不同性別對共享單車的需求情況不一樣,公民的受教育程度也影響著單車需求量,為此,我們考慮不同的年齡段、男女性別以及受教育程度這幾個因素,建立計算模型,如下:
參考《白皮書》的數據,男性對共享單車的需求大于女性,受教育程度較高的人群對共享單車的需求量更高,本文設置女性對共享單車的需求比例為 7%,男性對共享單車的需求比例為8%,受教育程度較高者對共享單車的需求比例為 8%,受教育程度較低者對共享單車的需求比例為 4%,建立以下人口模型計算公式:
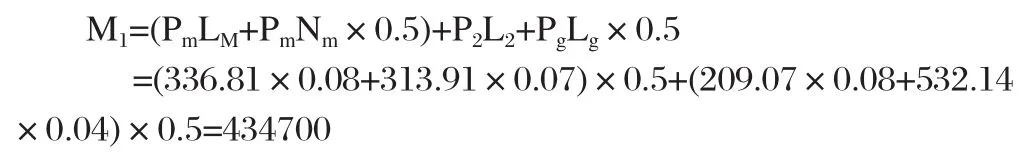
式中:Pm表示南京市15~64歲人口數量;Lm表示男性對單車需求比例;Nm表示女性對單車需求比例,P2表示大學專科(含專科)以上學歷;Pg表示大學專科以下學歷;L2表示大學專科(含專科)以上需求比例;Lg表示大學專科以下需求比例。
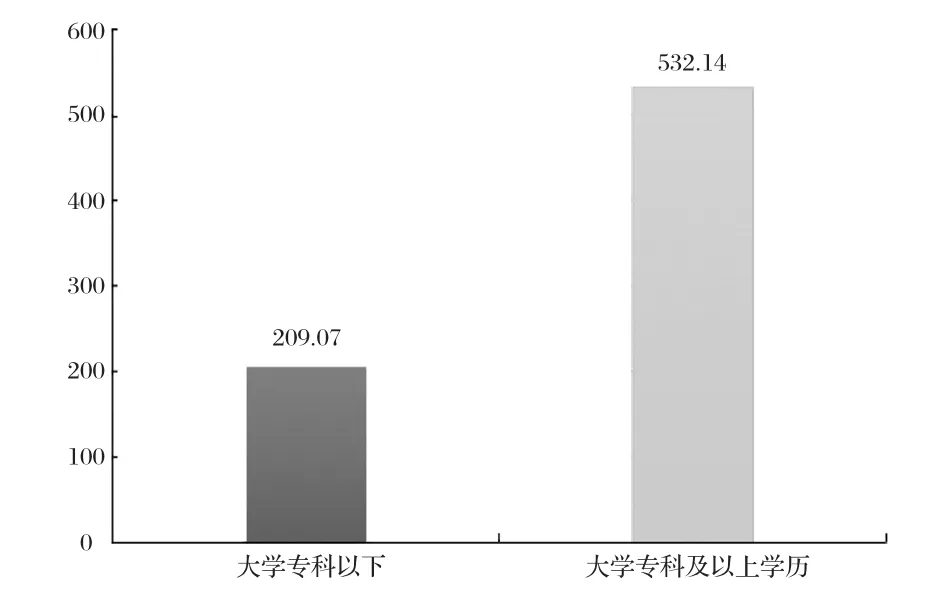
圖2 南京市第六次人口普查受教育程度(萬人)
共享單車的需求量可以從南京市的區域分布中反映出來。由于夜晚共享單車在南京的使用量較小,所以我們收集夜晚單車的輻射數據進行分析。
由于南京市城區分區較多,因此本文采用分區法,匯總各區地域的輻射數據,并統計各區域單車密度ρ(輛/km2)、區域面積,另外,本文也考慮到共享單車的需求量與測得的單車密度、區域面積有一定的比例關系, 需設比例系數C,該比例系數與區域的經濟發展水平有關,大致與該地區GDP呈線性相關, 建立簡單模型(C*代表南京各分區GDP,C總代表南京市總GDP)。
由此可以建立如下計算模型:
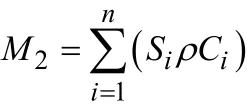
式中:n—南京市城區各分區數量;iSρ—分區面積;ρ—單車密度(輛/km2),iCρ—比例系數,根據數據分析,本文設置ρ=800(輛/km2)。通過查閱相關資料可知南京城區面積(km2)劃分如下:雨花臺134.6(2%),建鄴82.7(1%),江寧1572.9(24%),鼓樓53.1(1%),棲霞381.88(6%),六合1485.5(22%),浦口912.3(14%),秦淮49.2(1%),溧水1067.3(16%),玄武80.97(1%),高淳802(12%);將數據代入上述模型,結果如下:
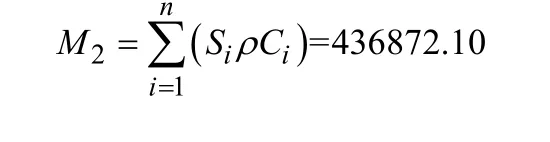
通勤市場計算共享單車的市場需求。軌道交通口、學校、各大商場以及旅游景點是使用共享單車高峰區,根據《白皮書》1分析數據,高達90%的居民會把共享單車與地鐵結合使用,本文選取公交站點、地鐵站點、學校、各大商場以及旅游景點為通勤市場,因此,本文依據通勤市場建立以下模型:M3= WdD + WgG + WxX+ WyY + WzZ ,其中代表地鐵站點的單車需求量,代表公交站點的單車需求量,代表高校對共享單車的需求量,代表商場對單車的需求量,代表旅游景點對單車的需求量,D代表地鐵站的數量,G代表公交站的數量,X代表高校的數量,Y代表商場的數量,Z代表旅游景點的數量,根據調查南京市的公交站點667個,地鐵站點139個,學校達359所(含高校及南京市區的各高中),大型購物商場279所,旅游景點59處,根據百度百科數據分析,南京市地鐵站單車需求量400輛,公交站點單車需求量40,每所學校的單車需求量400輛,購物商場單車需求量300輛,大型的旅游景區單車需求量800輛,將數據代入前者建立的模型: M3= WdD + WgG + WxX+ WyY + WzZ =356780。本文中的三個模型,分別在時間和空間上對共享單車的需求量進行討論,這3個模型處于同等地位,因此取其平均值可以得出南京市的單車需求量:由此得出南京市對共享單車的需求量大約為40.95萬輛。
2.2 共享單車分配的分析
共享單車數量在不同地區的分配趨于合理性,即已知在該地區共享單車的總數量,對其進行合理分配。本文主要通過考慮地區特點的差異影響到該地區共享單車的分配數量,建立相關模型,影響共享單車分配數量的因素有很多,如人流量越大的地區共享單車分配的數量比例就越高,同時不能單方面考慮某一因素的直接影響,要綜合考慮各方面因素,結合需求量與分配量的關系,運用組織結構圖,AHP(層次分析法)合理的進行單車分配。
AHP法是一種定量與定性相結合的,系統化層次化的分析方法,由美國匹茲堡大學 T·L·Satty 教授于20世紀70年代提出。所謂層次分析法, 是指將一個復雜的多目標決策問題作為一個系統,將目標分解為多個目標或準則,進而分解為多指標(或準則、約束)的若干層次,通過定性指標模糊量化方法算出層次單排序(權數) 和總排序,以作為目標(多指標)、多方案優化決策的系統方法。在此問題中,運用AHP法能夠有效解決投放單車數量更加偏重于哪方面因素的影響的問題。
圖3 單車投放點選擇示意圖
根據專家分析評估排定各評定指標的相對優劣順序,構造出評定指標的判斷矩陣:
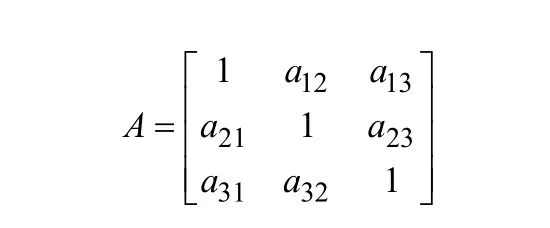
式中:A—判別矩陣,aij—要素i與要素j重要性比較結果,并且有如下關系:aij有9種取值,分別為1/9,1/7,1/5,1/3,1/1,3/1,/5/1,7/1,9/1,分別表示i要素對于j要素的重要程度由輕到重。運用規范列平均法求出權重向量,將矩陣A每一列歸一化得到矩陣B:;對矩陣B按行求和,即W=(W1,W2,W3,…Wn),將向量歸一化,即計算最大特征根,矩陣C即所求權重向量;假設某一地區預計投放共享單車Z輛,根據上述算法算得:C=[C1, C2, C3, C4, C5, C6, C7,C8]T;即可根據公式大致求得Z投放=ZC。通過上述運用AHP法計算出人流量大小,使用單車意愿,其他出行方式選擇等因素對投放點投放單車數量的影響權重,進而規劃分配該投放點的單車數量使單車的分布趨于合理。
2.3 共享單車調度的分析
基于上述分析給出共享單車的分配方案可知,南京共享單車主要有四大類投放點,本文給出的調度方案基于此四類投放點。單車的調度一方面在于公司規模化地進行調度,另一方面,由于單車的流動性也可以實現單車的調度,由此建立BP神經網絡模型進行分析。
簡要分析在該地區內四類主要單車投放點(共建點、居住點、交通樞紐、校園)之間的調度問題。暫且假設:第1類投放點:共建點,第2類投放點:居住點,第3類投放點:交通樞紐,第4類投放點:校園。四者關系如圖4所示。
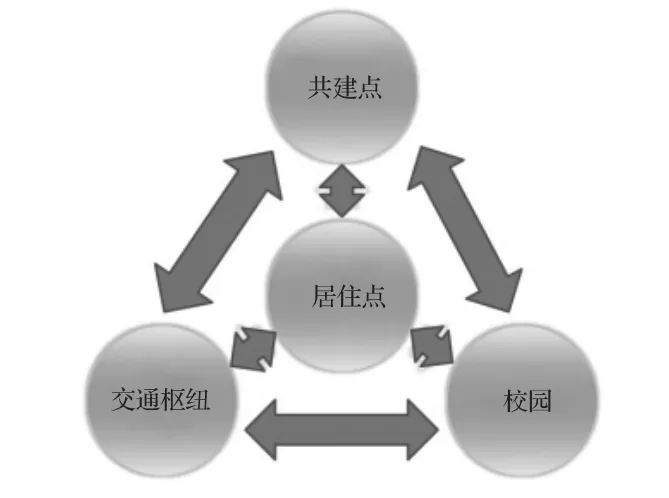
圖4 動態平衡示意圖
在給出具體調度方案后,四類單車投放點中的任意兩類投放點都能達到單車數量的一個動態平衡,為達此目的,我們建立整數規劃模型 :∑ Xij= N(i, j = 1 ,2,3,4,i ≠ j );其中,Xij表示第i類投放點需要調度(包括單車數量的增加以及減少)到第j類投放點的單車數量,調度后才能達到第i類投放點單車數量上的動態平衡(Xij≥0),例如,X12代表第1類投放點調度到第2類投放點的單車數量;N代表該四類投放點總共調度的單車數量。Xij的確定:首先考慮共享單車在投入后,公民騎行的流動性,實現了一部分的調度;其他因素對共享單車的調度不產生很大影響,最終,為達到各區域共享單車數量上的動態平衡,需要企業規模化地對單車進行調度。
針對公民騎行,使單車流動至各類單車投放點,建立同心圓模型。根據查詢資料可知,共享單車最遠騎行距離為5km,且由實際調查分析可知,南京市區單車投放點較為集中,該四類單車投放點兩兩間距離不會超過5km。因此將會有一大部分共享單車在各區域流動。選取第i類投放點為中心,第i、j類投放點距離為半徑r(r不超過5km)做圓再以5km為半徑做圓,得到同心圓,建立同心圓模型如圖5所示。
圖5 同心圓模型示意圖
從而可得共享單車具體調度方案為第i類投放點的企業調度數目:Ni=Mi-;求解得四類區域總共需調度得共享單車數量:

