簡化積分計算的一類方法
陳丹丹
在《高等數學》的學習中,很多人會被一些積分難題困擾.本文就探討了一類簡化積分計算的方法,利用積分區域的對稱性和被積函數的奇偶性簡化積分計算.
1 利用積分區間對稱性和被積函數奇偶性簡化定積分計算
根據定積分的定義和性質,可以利用牛頓—萊布尼茲公式:如果F(x)是連續函數f(x)在區間[a,b]上的任意一個原函數,則有f(x)dx=F(b)-F(a).
換元積分法和分部積分法也是求定積分的基本方法.我們在研究定積分的計算方法的過程中,發現利用積分的對稱性和被積函數的奇偶性是簡化定積分計算的一個重要方法,對此我們有如下定理:
定理1 設f(x)在[-a,a]上連續,若f(x)為偶函數,則
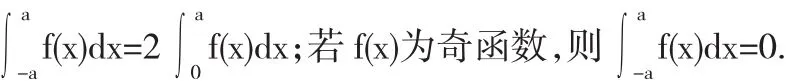
2 利用積分區域對稱性和被積函數奇偶性簡化二重積分計算
二重積分的計算方法是根據計算體積的原理,將它化為累次積分來計算的,因此,定積分中利用積分區域的對稱性和被積函數的奇偶性計算積分的方法,也可推廣到二重積分上.
定理2 設f(x,y)在有界閉區域D上可積,
同理也可以推出D關于y軸和關于x軸y軸對稱結論.
由該方法可以減少累次積分的計算量,使一些看上去復雜的積分問題簡單化,為利用對稱性,有時需將被積函數分拆分,將積分區域分成若干個對稱子區域.
例 2 設 D 是平面上以 A(1,1),B(-1,1)和 C(-1,-1)為頂點的三角形,D1是它的第一象限部分,則
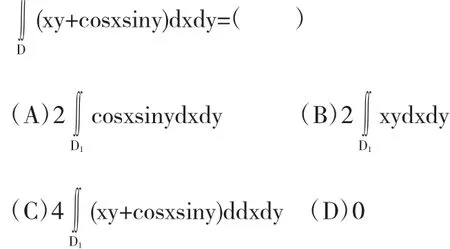
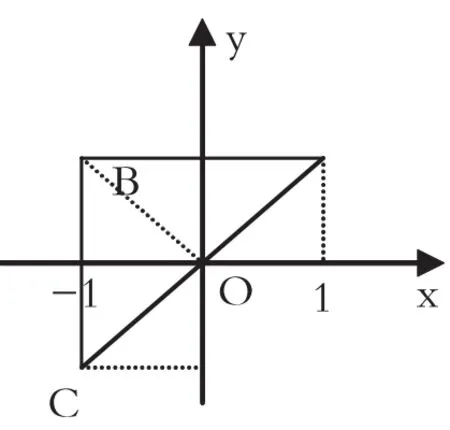
解 如圖所示:連接BO,把 D 分成 D'1∪D2,D'1即三角形 AOB,D2即三角形COB.由于D'1關于y軸對稱,被積函數xy關于x為奇函數;關于x軸對稱,xy關于y為奇函數.
而D'1關于y軸對稱,被積函數cosxsiny關于x軸為偶函數,D2關于x軸對cosxsiny關于y為奇函數.所以
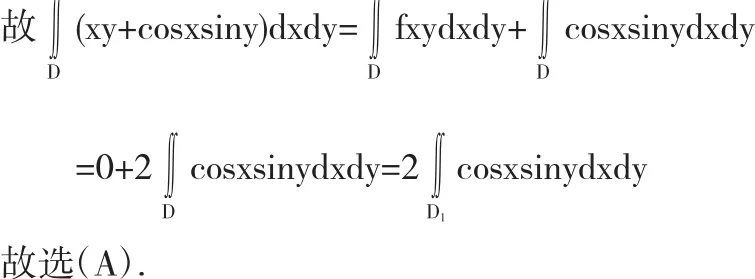
3 利用積分區域對稱性和被積函數奇偶性簡化三重積分計算
三重積分相對復雜,也可以利用積分區域的對稱性和被積函數的奇偶性來簡化積分計算,并且該方法也是計算三重積分的一個重要方法,其規律如下:
定理3 設f(x,y,z)在Ω上連續,若Ω關于平面xoy對稱,則當函數f(x,y,z)是z的奇函數,即f(x,y,-z)=-f(x,y,z)時,有;當函數f(x,y,z)是z的偶函數,即f(x,y,-z)=f(x,y,z)時,有f(x,y,z)dv;其中Ω1是Ω內z≥0的部分.同理可以得出Ω關于平面xoz對稱和關于平面yoz對稱的結論.
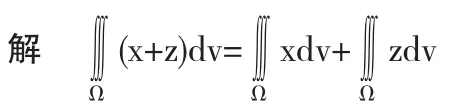
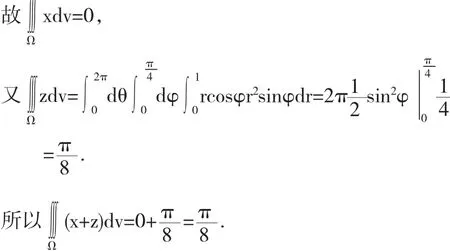
三重積分的計算,一般來說都需要計算多步,有的被積函數甚至比較繁,但如果能用上“對稱性”,則可能會收到意想不到的效果,但在利用“對稱性”的同時,也不能忽略被積函數的奇偶性.
4 利用積分區域對稱性和被積函數奇偶性簡化曲線積分計算
曲線積分和曲面積分是多元函數積分學的另一重要內容.同樣可以利用區域對稱性和被積函數的奇偶性來簡化它們的計算.
定理4 設f(x,y)是定義在光滑或分段光滑的曲線L上
的連續函數.若曲線L關于x軸對稱,則 ∫Lf(x,y)ds=2∫L1f(x,y)ds,當f(x,y)關于y是偶函數,L∫f(x,y)ds=0,當f(x,y)關于y是奇函數,其中L1是L在y≥0的那段曲線,即L1是L在上半平面的部分.
同理可以得出L關于y軸對稱和關于原點對稱的結論.
解 由于xy關于x(或y)為奇函數,且橢圓L關于y軸(x軸)是對稱的,所以L∮xydx=0,只需計算L∮(3x2+4y2)ds.又由于橢圓L可表示為3x2+4y2=12,所以有L∮(2xy+3x2+4y2)ds=(3x2+4y2)ds=12L∮ds=12a.
可見,利用對稱性和被積函數的奇偶性也可簡化第一類曲線積分的計算.類似于第一類曲線積分,第二類曲線積分也有如下一些性質:
若L∫Pidx+Qidy(i=1,2,…,k)存在,則也存在,且Qidy),其中 ci(i=1,2,…,k)為常數.
若有向曲線L是有向曲線L1,L2,…,Lk,首尾相接而成,且Pdx+Qdy(i=1,2,…,k)存在,則 ∫LPdx+Qdy也存在,且 ∫LPdx+Qdy=
同樣可以利用積分區域的對稱性和被積函數的奇偶性簡化第二類曲線積分的計算.
定理5 設L為平面上分段光滑的定向曲線,P(x,y),Q(x,y)連續,
(1)若L關于x軸對稱,并且L1為L在上半平面的部分,
則
∫LPdx=0,當P關于y為偶函數,∫LPdx=2∫L1Pdx,當 P 關于y為奇函數;
∫LQdy=0,當Q關于y為奇函數,∫LQdy=2∫L1Qdy,當Q關于y為偶函數;
同理可以得出L關于y軸對稱和關于原點對稱的結論.
(3)若L關于原點對稱,則L∫Pdx+Qdy=0,當P,Q關于(x,y)為偶函數,∫LPdx+Qdy=2∫L3Pdx+Qdy,當P,Q關于(x,y)為奇函數.
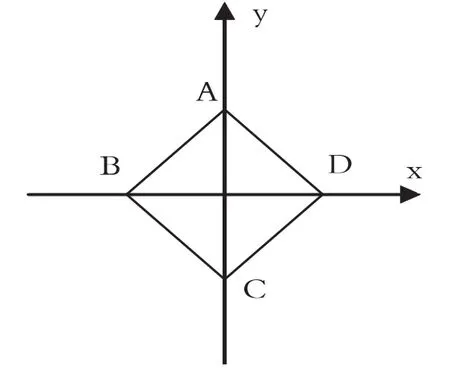
解法1 將原式分為兩部分
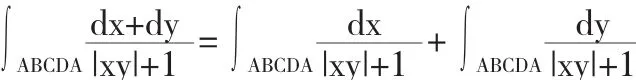
因第一個積分曲線關于x軸對稱,且走向相反,被積函數為y的偶函數,第二個積分曲線關于y軸對稱,且走向相反,被積函數為x的偶函數,所以兩積分值均為0,即
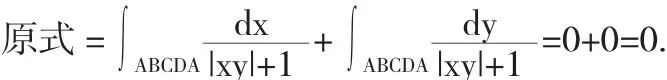
解法2 因曲線ABCDA關于原點對稱,又P(x,y)=Q(x,y)關于(x,y)為偶函數,所以原式=0.
5 利用積分區域對稱性和被積函數奇偶性簡化曲面積分計算
曲面積分分為第一類曲面積分和第二類曲面積分,第一類曲面積分的性質完全類似于第一類曲線積分的性質.第一類曲面積分利用對稱性有如下定理.
定理6(1)若分片光滑的曲面∑關于xoy平面對稱,且∑1:z=z(x,y)≥0,則

同理可以得出分片光滑的曲面∑關于xoz平面對稱和曲面∑關于yoz平面對稱的結論.
解 因為∑關于xoy平面對稱,且sinxsinysinz是z的奇函數,所以sinxsinysinzds=0.
第二類曲面積分的性質也完全類似于第二類曲線積分的性質,且第二類曲面積分奇偶對稱性的說法與第一類曲面積分有所不同,在積分曲面關于某坐標面(例如yoz面)對稱的前提下,第一類曲面積分的說法是:被積函數(關于x)為奇函數時積分值為0;而第二類曲面積分的說法是:被積函數(關于x)為偶函數時積分值為0.
定理7 設分塊光滑定向曲面∑關于xoy平面對稱,f(x,y,z)在∑上連續,則f(x,y,z)dxdy=0,當f關于z為偶函數,f(x,y,z)dxdy=2f(x,y,z)dxdy,當f關于z為奇函數,其中∑1為∑在xoy平面上方部分,其方程為z=z(x,y),(x,y)∈Dxy.
同理可以得出分片光滑的曲面∑關于xoz平面對稱和曲面∑關于yoz平面對稱的結論.
證明 由第二類曲面積分的可加性,有
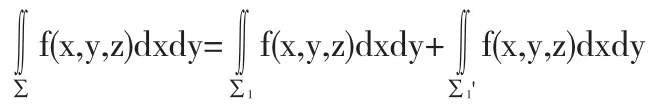
其中∑1為∑在xoy平面上方部分,其方程為z=z(x,y),(x,y)∈Dxy,∑1'為∑在xoy平面下方部分,其方程為z=-z(x,y),(x,y)Dxy.
由分塊光滑定向曲面∑關于xoy平面對稱可知:
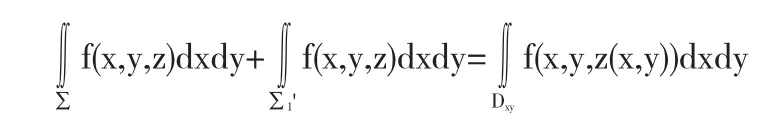

若f(x,y,z)關于z為奇函數,
則
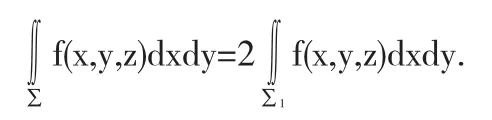

由于x2+y2+x2≤1,關于平面y=0對稱,siny為y的奇函數,故
6 結束語
綜上所述,利用此方法簡化此類積分的計算,但具體使用上有所不同.在二重積分,三重積分的計算中,是利用積分區間的對稱性及被積函數的奇偶性來簡化計算.在第一類曲面積分中,若積分區間內關于某坐標平面對稱,而被積函數是另一變元的奇函數,則其積分值為0.在第二類曲面積分,若積分曲面關于其面積元素兩個同名變元的坐標平面對稱,而被積函數又是另一變元的偶函數,則其積分值為0.如果能合理有效地運用積分區域的對稱性和被積函數的奇偶性來簡化此類積分的計算,那么解決許多之前似乎不易解決的問題就會變得又快又準確.

