外部電場對三角束縛勢量子點量子比特概率密度的影響

尹輯文

1 引言

近年來，各領域的科學研究者們將量子理論應用于物質科學和能源科學，開拓出諸如半導體、激光、核技術等重要高新技術.本世紀，一門新興的交叉學科——量子信息科學應運而生，它是量子力學與信息科學相互融合的結果.在過去幾年里，對不同物理系統用做量子信息載體，人們進行了諸多的理論和實驗研究[1-8].由于各種物理系統應用于量子計算機各有利弊，人們目前正在尋找影響量子計算機性能的各種因素.本論文以Li等人[9-10]提出的參數相圖方案為前提，研究討論了外部電場對三角束縛勢量子點量子比特的概率密度的影響.

2 理論模型

設在單一電子量子點中,電子在z方向比x和y方向受限強得多，設電子在x-y平面內運動，僅考慮電子-體縱光學聲子耦合，電子的束縛勢為三角束縛勢可寫為

其中m*為電子的有效質量,ρ為二維坐標矢量,ω0為量子點的受限強度,沿x方向加電場F，則在電場作用下電子-聲子體系的哈密頓量為

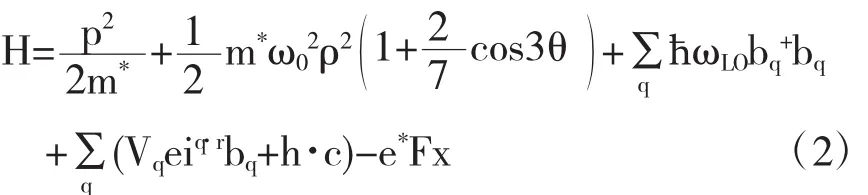
其中bq+(bq)為波矢為q(q=q∥,q⊥)的體縱光學聲子的產生(湮滅)算符,r=(ρ,z)為電子坐標矢量,e*是電子電荷

為了計算方便，采用極化子單位(?=ωLO=2m*=1)，系統的哈密頓量可以寫為

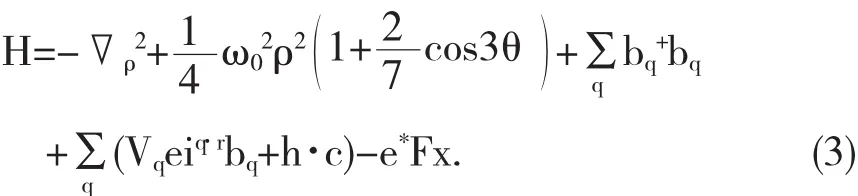
其中

α為電子-LO聲子的耦合強度.

對哈密頓量(3)作LLP變換

其中fq是變分函數，則

在高斯函數近似下，依據Pekar類型的變分法，電子-LO聲子系統的基態嘗試波函數可以選為

電子-LO聲子系統的激發態嘗試波函數可以選為

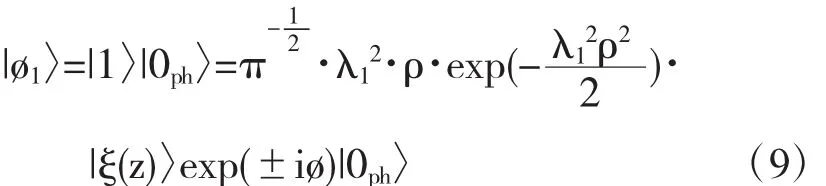
其中，λ0和λ1為變分參量，|0ph〉為無微擾零聲子態，bq|0ph〉=0，|0〉、|1〉滿足

由 E0=〈?0|H"|?0〉，E1=〈?1|H"|?1〉通過分法可以得到變分參量λ0和λ1，進而可得到基態和激發態能量及其本征波函數，得出了一個量子比特所需要的二能級體系，當電子處于這樣一個疊加態

疊加態隨時間的演化可以表示為：

3 結果和討論

為了更直觀的看出電場對三角型量子點量子比特的影響，數值結果表于如下圖中.

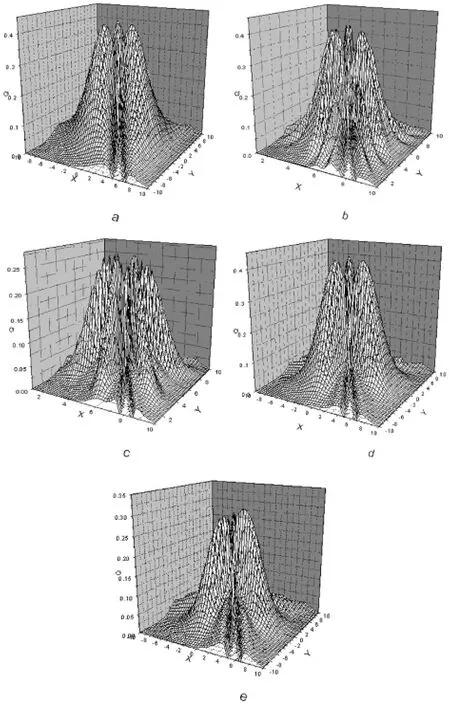
圖1（a-e）電子在空間的概率密度分布隨時間的演化

圖2 概率密度Q隨電場強度F和電子-聲子耦合強度α的變化關系

圖2 給出的是受限長度θ=0.2、極角為θ=0.2時，概率密度Q(ρ，θ，t)隨電場強度F和電子-聲子耦合強度α的變化關系.從圖2可以看出，概率密度 Q(ρ，θ，t)隨著耦合強度增大而增大.同時從圖中可以看出概率密度Q(ρ，θ，t)隨著電場的增加而減小.并且電子-聲子耦合強度越大，電場強度F對概率密度 Q(ρ，θ，t)的影響越明顯.由于電場的存在約束了基態和第一激發態的能量，同時電場對激發態能量的影響比對基態能量的影響要明顯，導致了能量差隨電場強度的增大而減小.

4 結論

本論文應用Pekar類型的變分方法，研究了電子與光學聲子的耦合強度、極角和電場對量子點量子比特概率密度的影響.研究發現，當極角取確定的值θ時，電子的概率密度將以一定周期在空間振蕩，是極角的周期性函數；概率密度隨電場強度的增大而減小，隨耦合強度的增大而增大.綜上，可以看出外部電場和電子與光學聲子的耦合強度對量子點量子比特的微觀性質有明顯的影響.