分裂導線伸張器的構型設計和仿真分析

曹 東

(中國南方電網有限公司超高壓輸電公司梧州局，廣西 梧州 543002)

0 引言

目前我國220 kV及以上電壓等級的高壓、超高壓及特高壓輸電線路每相導線采用了2根及以上的分裂導線。在檔距中相隔一定距離安裝了防護金具——間隔棒，以保持分裂導線線束間距不變，來滿足降低表面電位梯度、減少電暈、增加電能輸送容量等電氣性能要求。

國家相關標準中規定間隔棒檢修周期為2年。在更換間隔棒過程中，傳統的方式是利用軟繩索及分裂導線之間的張力確定導線之間的檔距，以便于間隔棒的拆卸與安裝。但由于繩索的固有屬性決定了其工作過程的不確定性，拆除間隔棒瞬間子導線的張力作用會使繩索迅速收緊，由此產生的突變載荷不利于導線系統的穩定。除此之外，作業人員的體重作用在作業附近的導線上，導致間隔棒爪與導線不可避免發生彎曲變形，從而使更換后的間隔棒偏離其正確的位置，不利于分裂導線間距的保持。針對間隔棒更換過程中存在的問題，提出了一種輔助間隔棒更換作業的器械構型。

1 分裂導線伸張器的構型設計

1.1 分裂導線伸張器的構型

分裂導線伸張器的結構如圖1所示，它屬于一種具有多個并行輸出的復合機構。第1級機構實現動力的輸入，由摩擦輪與摩擦錐之間的高副接觸實

現動力的傳遞，同時由于摩擦錐的特殊形狀可以完成傳動比的無級變化，因此可以根據現場需要調整機構的輸出效率。第2級機構為定軸齒輪傳動，傳動比不發生變化，可完成機構多個并行的同步輸出，且收放輪的轉向相同，因此可以實現多根分裂導線的同步操作。

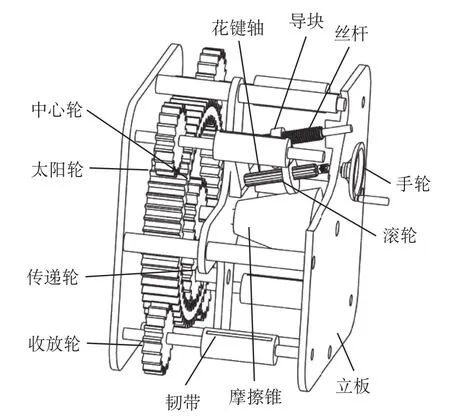
圖1 分裂導線伸張器結構示意

1.2 分裂導線伸張器的運行和關鍵參數

分裂導線伸張器的運動示意如圖2所示。由圖可知本機構分為2部分：一部分為具有螺旋進給的摩擦輪摩擦錐式無級變速機構；另一部分為定軸齒輪傳動機構。定軸齒輪機構部分的主要參數為各輪齒數配置，無級變速部分的滾輪半徑r、摩擦錐的錐底半徑R″、花鍵軸與主軸的夾角θ以及摩擦輪與摩擦錐的摩擦系數為影響機構運動特性的主要參數。相應參數的符號和含義如表1所示。其中影響摩擦輪與摩擦錐之間摩擦力的因素較多，也決定了機構的傳遞效率和極限載荷，是建立機構動力學模型的主要研究對象。

圖2 分裂導線伸張器的運動示意

表1 簡圖參數的符號和含義

2 分裂導線伸張器構型的理論分析

2.1 運動學方程的建立

伸張器的操作特性與其構型的傳動原理和功能尺寸密切相關，為深入認識無級變速部分對傳動比的影響機理，并在此基礎上優化結構的功能尺寸，必須建立機構的運動學模型。求解過程分2個部分：定軸齒輪傳動比方程和無級變速部分傳動比方程。摩擦錐和中心輪共軸安裝，因此2者的轉速相同，由此實現2部分的傳動比銜接，最后在定軸齒輪傳動鏈條的末端求收放輪(即韌帶)的運動學方程。

設摩擦輪從摩擦錐大端的D點開始運動，當其由D點運動至K點時絲桿轉過的距離為ψ，此時摩擦輪與摩擦錐的傳動比為

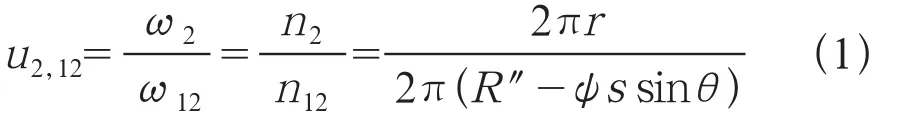
式中：ω12，n12為摩擦錐的角速度和轉速；ω2，n2為摩擦輪的角速度和轉速；s為絲桿的螺紋導程；ψ為摩擦輪由接觸點D移動到K點時，絲桿轉過的角度。

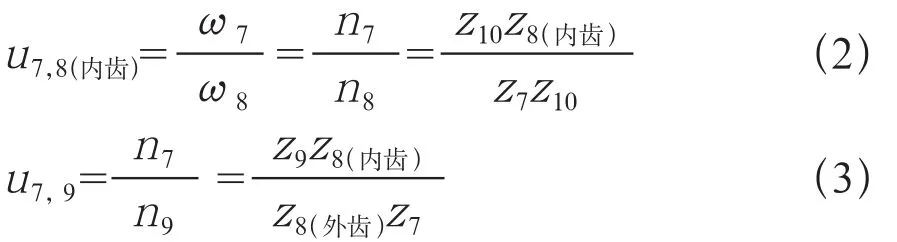
于是摩擦輪與收放輪之間的傳動比為

2.2 滾輪摩擦力及摩擦驅動力矩的計算

摩擦輪與摩擦錐的母線接觸，在接觸位置發生變形后可以將接觸區域簡化為矩形，設接觸區長為l, 摩擦輪半徑為r；因為是小變形則假設其接觸仍為平面接觸，則接觸壓力分布在該區域上，如圖3所示。

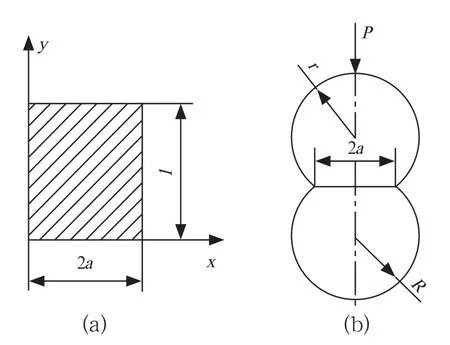
圖3 滾輪與摩擦錐的接觸區域

接觸區域的壓力為

其中:

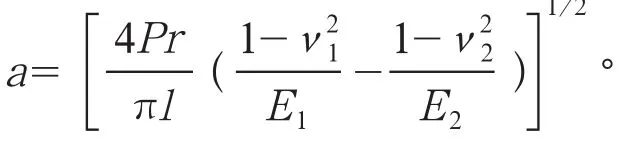
式中:p為接觸面的法向作用力;a為接觸區域寬度的一半;v1,v2為摩擦輪和摩擦錐的泊松比比;E1，E2為摩擦輪和摩擦錐的彈性模量。在距離接觸中心x(x＞0)的地方取一寬為dx，長為l的帶狀單元,則在此單元上產生的彈性力為

可得彈性力對滾動中心產生的力矩為

魯迅早期是個革命民主主義者，進化論思想是他主導思想，他相信“將來一定超過現在”。他這種認識與當時的社會條件是相符合的，當時，工人階級還沒有作為一支獨立的政治力量登上歷史的舞臺，因此，魯迅還不明確中國革命應當由中國工人階級領導，以工農聯盟為基礎；尤其是對工人階級力量沒有深刻的認識；他還沒有把實現共產主義作為自己的社會理想；還不是一個共產主義者。但是，那時的魯迅對農民階級已經有了深刻的認識。他不僅看到了農民身上存在缺點，也發現了農民具有的優秀品德，意識到農民群體的偉大力量，察覺到沒有農民參加的社會革命是不可能成功的。

則x＞0的區域對滾動中心的阻力矩為

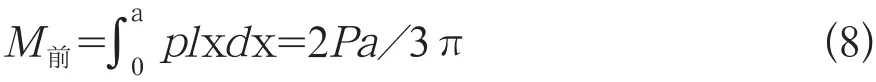
由于現實中摩擦輪與摩擦錐均采用粘彈性材料，因此M前≠M后，2者的差值|M前-M后|即為材料彈性滯后所產生的阻力矩。為簡化計算，在M前中引入系數α作為綜合力矩：

于是，當圓柱體滾過距離x時M總的功耗為

由于最外層的粘接點只有被拉斷才會脫離接觸，因此其拉應力為軟材質的強度極限σb。滾動中心的粘接點受拉力為0，因而可以認為接觸中心拉應力為σs，粘接點層的應力分布近似為線性分布，應力的方程式為

則可求得：

式中：δ為實際接觸面積與幾何面積之比。

則由粘性阻力所產生的功耗為

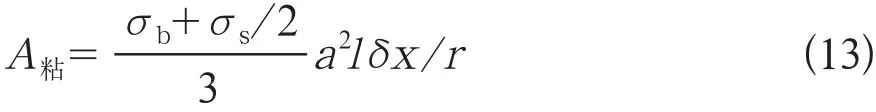
于是由摩擦所產生的總能耗為

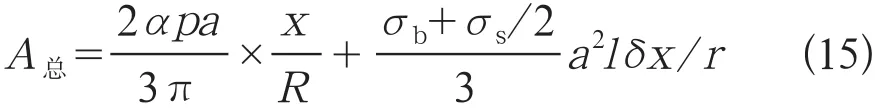
庫侖在研究摩擦力時提出：滾動摩擦阻力系數為驅動力在單位距離上所做的功與法向載荷之比，滾動摩擦系數為滾動摩擦阻力系數與滾動半徑的乘積。于是滾動摩擦阻力系數為

滾動摩擦系數為

故摩擦輪對摩擦錐的驅動力及驅動力矩為

式中：p為正壓力；Δh為摩擦輪與摩擦錐接觸點到摩擦錐轉動中心的距離。

3 分裂導線伸張器的虛擬樣機分析

3.1 建立虛擬樣機

因Adams本身自帶的幾何建模模塊不夠精準和逼真，且整個樣機零件較多時建模工作會耗費大量的時間，因此預先在Creo2.0中完成整機的三維建模與裝配，隨后導入至Adams中，并將其中一些零件運用布爾運算簡化為一個構件，以提高仿真效率。分裂導線伸張器的虛擬樣機如圖4所示。

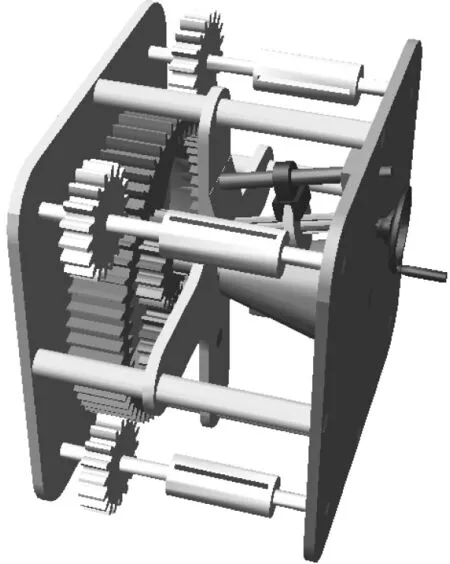
圖4 分裂導線伸張器的虛擬樣機

各構件的約束類型如表3所示。隨后對系統自由度、未定義重量構件和過約束等情況進行檢查。

表3 導線伸張器各構件的約束類型

3.2 仿真分析

調用Adams/Solver進行仿真分析以獲得構件的運動特性。為節省計算機資源，將仿真時間設置為End time為1.5 s，步數為500，摩擦輪的驅動函數為30d*time，絲桿導程為2 mm,然后進行仿真。在仿真過程中，撥塊同時以2 mm/s的速度驅動摩擦輪移動。在仿真計算結束后進入后處理環境進行處理，獲得摩擦錐速度、收放輪(即韌帶)收放速度、摩擦輪與摩擦錐的傳動比的變化曲線，如圖4—6所示。

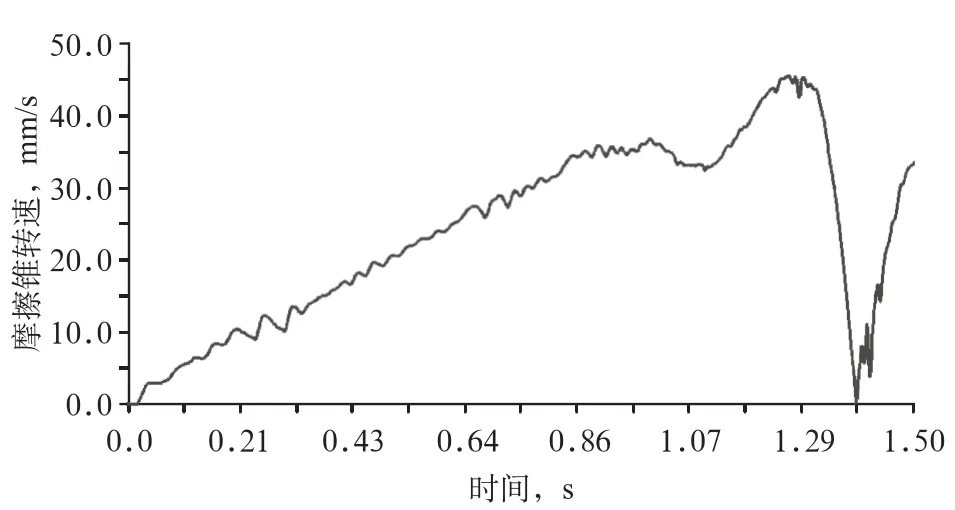
圖4 摩擦錐轉速隨時間的變化曲線

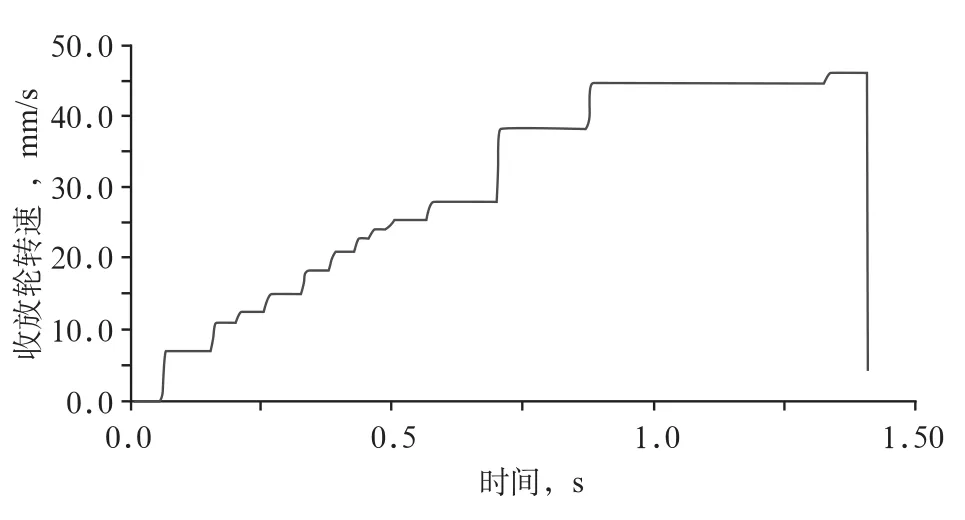
圖5 收放輪轉速隨時間的變化曲線

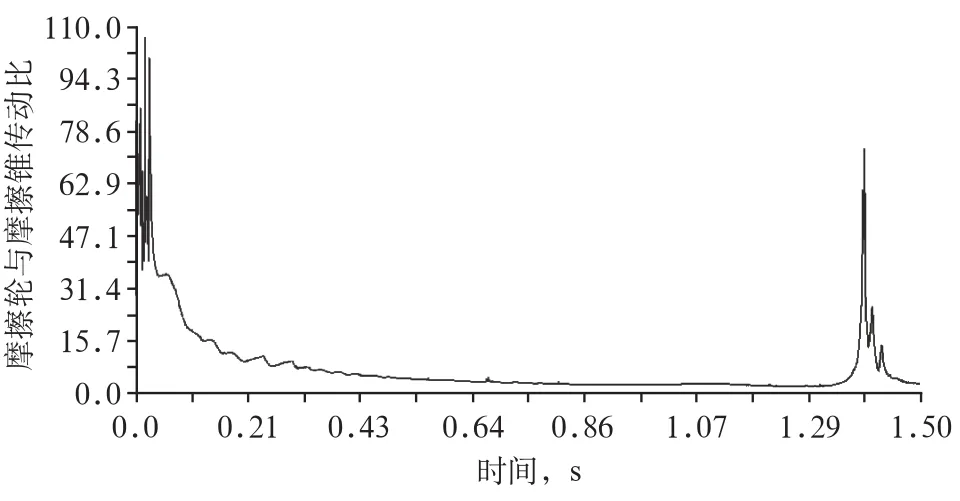
圖6 摩擦輪與摩擦錐傳動比隨時間的變化曲線

摩擦錐的轉速是在摩擦輪轉動與沿著花鍵軸移動2種運動并存的情況下獲得的。由圖4可知，摩擦錐的轉動速度是逐漸上升的，在1.29 s時達到峰值。盡管在這一過程中有小幅波動的情況出現，但總體呈現近似線性變化的規律。其變化規律與傳動比減小的趨勢相符，說明撥塊能較好地調整摩擦錐的轉速。但是曲線的小幅波動說明裝置在工作過程中存在顫震現象，如果波動幅度增加，則會降低系統的穩定性和承載能力。

圖5為收放輪的轉速變化曲線，反映了控制分裂導線的韌帶的運動狀況。由圖5可知，隨著摩擦輪與摩擦錐之間傳動比的減小，韌帶的收放速度逐漸增加，與傳動比的變化規律相對應。曲線中的“平臺保持”是由于絲桿轉動時動時靜導致的。這一仿真缺陷卻恰好反映了保持摩擦輪位置不變時系統的傳動比穩定。

圖6變化規律與圖4摩擦錐轉速的變化規律基本對應。由于仿真過程中摩擦輪逐漸向摩擦錐的小端移動，根據式(1)的計算，摩擦輪與摩擦錐的傳動比是按有效積溫函數變化而逐漸減小的，仿真結果與預期相符，證明改變裝置內部傳動比的可行性。

4 結論

(1) 通過理論分析可知，摩擦輪與摩擦錐之間的傳動比是變化的，且隨著摩擦錐頂角和絲桿導程(即撥塊的移動速度)的增大而降低；摩擦系數與彼此的微接觸面的寬度成正比，與摩擦輪的半徑成反比，因此適當增加2者材料的彈性變形能力和減少摩擦輪的半徑，可增大摩擦力矩。

(2) 通過仿真分析可知，傳動比的變化規律與式(1)所體現的規律一致，撥塊能順暢地調整摩擦輪與摩擦錐之間的傳動比，因此在實際使用中操作者可以根據實際需要調整操作效率。