全國名校等差數列拔高卷(B卷)答案與提示
一、選擇題
1.B 2.A 3.C 4.D 5.A 6.B 7.C 8.B 9.D 10.C 11.A 12.B 13.B 14.B 15.A 16.B 17.C 18.C 19.B 20.B 21.B 22.A 23.C 24.B 25.A 26.C 27.D 28.C 29.A 30.C 31.C 32.A 33.A 34.A 35.A 36.C 37.A
二、填空題
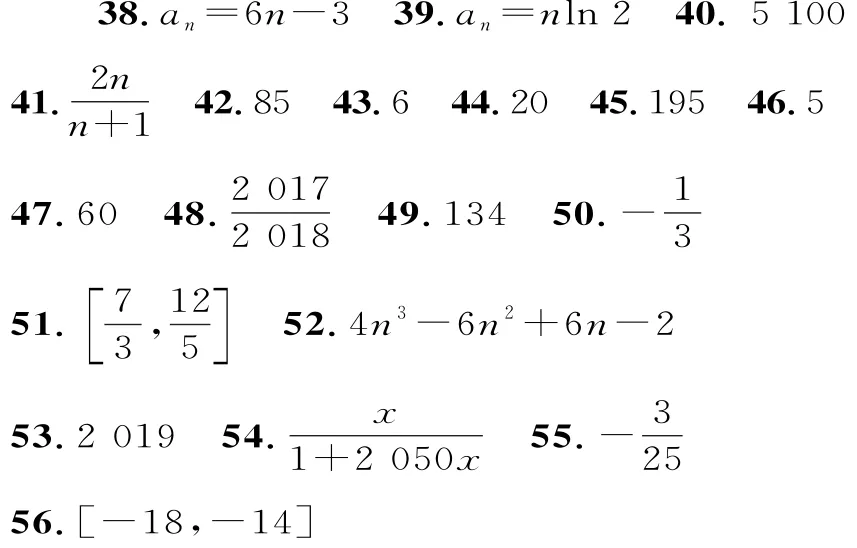
三、解答題
57.設公差為d,由a1=20,S10=S15,解得公差d=-5。3
因為S10=S15,所以S15-S10=a11+a12+a13+a14+a15=5a13=0,a13=0。
因為公差d<0,a1>0,所以a1,a2,…,a11,a12均為正數,并且a14及以后各項均為負數。
故當n=12或13時,Sn有最大值為S12=S13=130。
58.(1)設{an}的公差為d,由題意得3a1+3d=-15。
由a1=-7,得d=2。
所以{an}的通項公式為an=2n-9。
(2)由(1)得Sn=n2-8n=(n-4)2-16。
所以當n=4時,Sn取得最小值,最小值為-16。
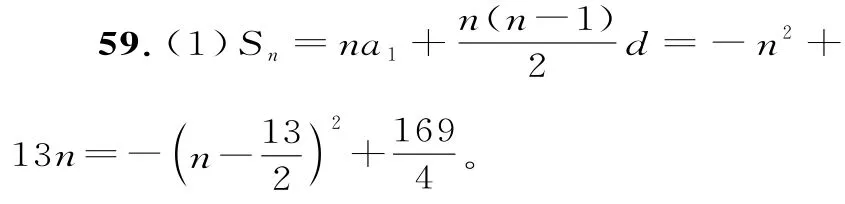
可畫出Sn的圖像,由圖像易得:
當1≤n≤6時,Sn單調遞增;
當n≥7時,Sn單調遞減。
Sn有最大項,最大項是S6=S7=42。
(2)由圖像可得當Sn>0時,1≤n≤12,故{Sn}有12項大于0。
60.由Sn=32n-n2,可得:
當n=1時,a1=S1=31;
當n≥2時,an=Sn-Sn-1=32n-n2-32(n-1)+(n-1)2=33-2n。
故an=33-2n。
令an≥0,則33-2n≥0,n≤16.5。
因為n∈N*,所以當n≤16時,an>0;當n≥17時,an<0。
本題Pn的求值應分兩種情況討論。
(1)當n≤16時,Pn=|a1|+|a2|+…+|an|=a1+a2+…+an=Sn=32n-n2。
(2)當n≥17時,Pn=|a1|+|a2|+…+|a16|+|a17|+…+|an|=a1+a2+…+a16-a17-a18-…-an=(-a1-a2-…-a16-a17-…-an)+2(a1+a2+…+a16)=-Sn+2S16。
因為S16=32×16-162=256,Sn=32n-n2,所以Pn=512-32n+n2。

整理得n2+13n-140=0,解得n=7或n=-20(舍去)。
故甲、乙開始運動后7分鐘相遇。
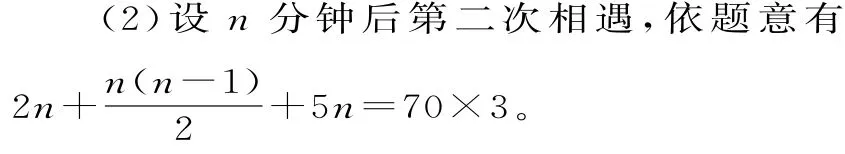
整理得n2+13n-420=0,解得n=15或n=-28(舍去)。
故第二次相遇在開始運動后15分鐘。
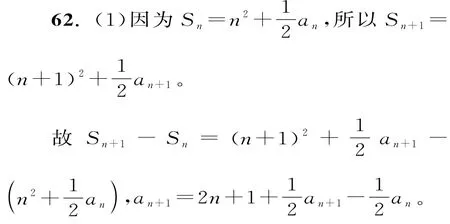
故an+1+an=4n+2。
(2)由(1)可知an+1+an=4n+2。
也即an+2+an+1=4(n+1)+2。
兩式相減可得an+2-an=4。
所以{an}中奇數項,偶數項分別為公差是4的等差數列。

由于n=2時,a2=p,n=1時a1=0,也適合該式,故對一切正整數n,an=(n-1)p。
因此,an+1-an=p。
由于p是常數,故數列{an}為等差數列。

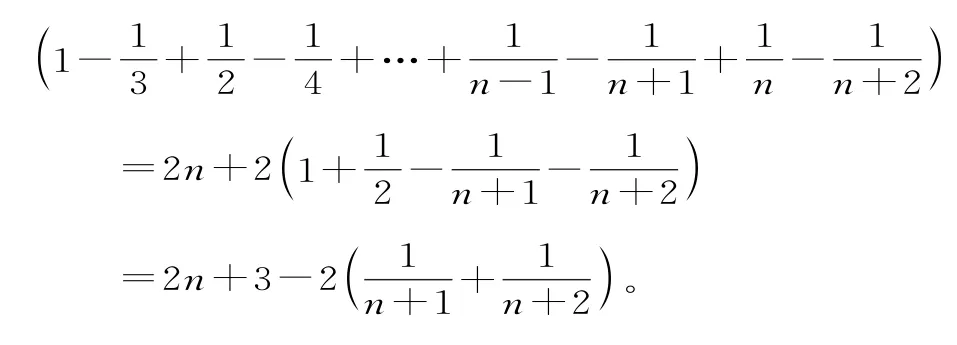
64.(1)根據題意,商家在11月1日至15日之間家電M每天的銷售量組成公差為t的等差數列{an}。

(2)設從11月1日起,第n天的銷售量最多,1≤n≤30,n∈N*。
由(1)知,若商家在11月1日至15日之間未提價,則這15天家電M的總銷售量為450臺。
而450>414,不符合題意,故n<15。
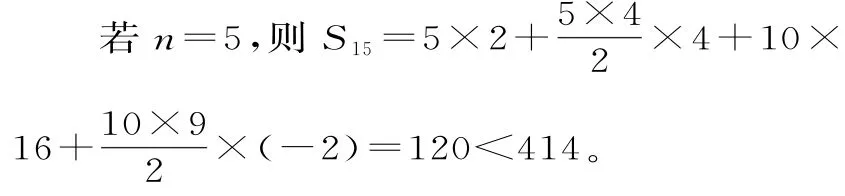
也不符合題意,故n>5。
因此,前n天每天的銷售量組成一個首項為2,公差為4的等差數列,第n+1天開始每天的銷售量組成首項為4n-4,公差為-2的等差數列。因此,
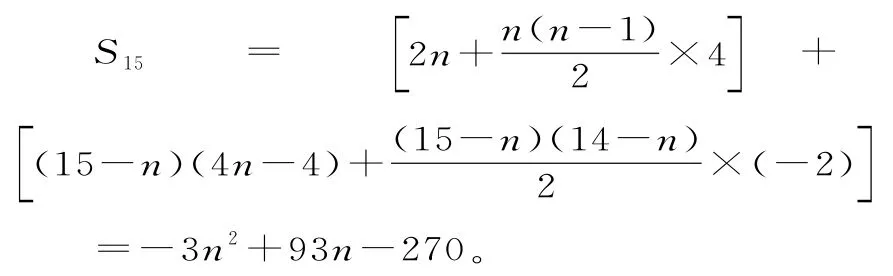
由已知條件,得S15=414,即-3n2+93n-270=414。
解得n=12或n=19(舍去)。
故n=12時,出售家電M的臺數為2+11×4=46(臺)。
故在11月12日,該商場售出家電M的臺數最多,這一天的銷售量為46臺。
65.(1)因為Sn=2an-2n+1,所以Sn-1=2an-1-2n(n≥2)。

f(n+1)>f(n),故f(n)為遞增數列。

66.(1)由題意可設Sn=An2+Bn,則Sk2
=A(k2)2+Bk2,Sk=Ak2+Bk。由Sk2=(Sk)2可得k2(Ak2+B)=k2(Ak+B)2,考慮到k為正整數,從而Ak2+B=A2k2+2ABk+B2,也即(A2-A)k2+2ABk+(B2-B)=0。
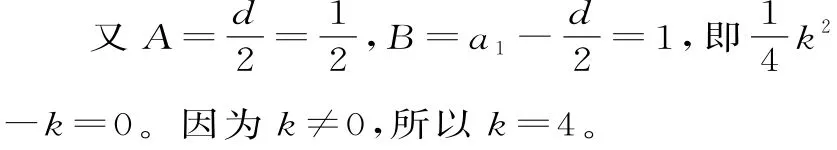


故滿足題意的無窮等差數列有:
①an=0,n=1,2,3,…;
②an=2n-1,n=1,2,3,…;
③an=1,n=1,2,3,…。

同理可得:

設q=2p-1,此時r=4p2-5p+2。
因為p≥2,所以q=2p-1>p,r-q=4p2-7p+3=4(p-1)2+p-1>0。故q=2p-1,r=4p2-5p+2。符合題意。
綜上所述,p=1時,不存在滿足條件的q,r;p≥2時,存在q=2p-1,r=4p2-5p+2。



