解三角形常見解題錯誤辨析
■四川省巴中中學 肖 斌(特級教師)
在利用正弦、余弦定理解三角形問題時,由于涉及的知識點多、綜合性強,許多同學易出現這樣或那樣的錯誤。下面分類列舉典例、辨析是非、集中警示,旨在幫助同學們夯實內功、優化思維、提高“免疫力”。
誤區一:粗心大意、忽視結論與題設的相容性,忘記代入檢驗致誤

所以B=45°或B=135°。
當B=45°時,AC2=AB2+BC2-2AB·BC·cosB=1,此時AC=1;
當B=135°時,AC2=AB2+BC2-2AB·BC·cosB=5,此時AC=。
辨析:上述解法,貌似無錯,殊不知,在審題時栽了跟頭。事實上,當B=45°時,AC=1,計算發現AC2+AB2=12+12=2=BC2,此時△ABC為直角三角形,不合題意;同理當B=135°,求得AC=,符合題意。故本題正確答案為AC=。
練習1 △ABC的內角A,B,C的對邊分別為a,b,c,已知cos(A-C)+cosB=,b2=ac,求B的大小。

誤區二:以偏概全、忽視分類討論致誤
例2 在△ABC中,A=60°,a=43,當此三角形有唯一解時,b滿足的條件是( )。

圖1

辨析:錯解中實際上只考慮了B≥A的情形。如果B<A,那么三角形也是有唯一解的。錯解正是受圖形影響、以偏概全產生了錯誤。
正解:若B<A,三角形有唯一解,只需0<b<43;
若B≥A,三角形有唯一解,只需bsinA=bsin60°=3b=a=43或b=a=43,即2 b=8或b=43。
綜上,0<b≤43或b=8,故選D。
練習2 △ABC的內角A,B,C的對邊分別為a,b,c,若sinC+sin(B-A)=sin2A,則△ABC的形狀為。
正解:因為sinC+sin(B-A)=sin2A,所以sin(B+A)+sin(B-A)=sin2A,整理得sinBcosA=sinAcosA 。當cosA ≠0時,則sinB=sinA,由正弦定理得b=a,此時△ABC為等腰三角形;當cosA =0時,則A=π,此時△ABC為直角三角形。故正確
2答案是:等腰三角形或直角三角形。
警示:同學們容易犯的錯誤是:得到sinBcosA=sinAcosA后,兩邊直接約去cosA ,得sinB=sin A,b=a,片面斷定三角形是等腰三角形,不知不覺中漏掉直角三角形的情況。還有一種錯誤是:雖然分類討論了,但最后答案卻寫成等腰直角三角形。殊不知,“等腰直角三角形”是“既是等腰三角形又是直角三角形”的含義,與“等腰三角形或直角三角形”有著截然不同的含義。
誤區三:忽視三角形中“小邊對小角,大邊對大角”隱含關系致誤
例3 (2017年高考全國Ⅲ卷文數第15題改編)△ABC的內角A,B,C的對邊分別為a,b,c,已知b=6,c=3,(1)若C=60°,則B=;(2)若B=45°,A=。

又B=45°,因此A=75°。
辨析:上述解法,忽視邊b<c,則角B<C的隱含信息。第一問求得想當然得到B=45°或B=135°,出現增解錯誤。第二問又沒有注意到角C有兩解,求得后,武斷認為C=60°,導致角A只有一解,造成漏解錯誤。

因為b<c,所以C>B=45°,C=60°或C=120°,故A=75°或15°。
警示:在△ABC中,A>B?a>b?2RsinA>2RsinB?sinA>sinB。


故△ABC是直角三角形。
警示:解此題同學們需防范兩類錯誤:一是由sin2A=sin2B,貿然得2A=2B,A=B,故△ABC是等腰三角形;二是雖由sin2A=sin2B,得出A=B或A+B=,但忽視b>a,錯誤地判斷△ABC是等腰三角形或直角三角形。
誤區四:顧此失彼、忽視進一步縮小角的范圍致誤
例4 (2015年高考湖南卷理數第17題)設△ABC的內角A,B,C的對邊分別為a,b,c,且a=btanA,B為鈍角。

(2)求sinA+sinC 的取值范圍。


辨析:上述解法在求解第(2)小題時,對角A的取值范圍顧此失彼、思考不深入導致錯誤。事實上,求解時除考慮A為銳角外,還需要考慮C為銳角,即需利用三角形內角和定理將角A、C的范圍轉化為關于A的不等式(組),進而縮小角A的范圍,獲得正確答案。
正解:(1)解題過程同上。

練習4 (由人教A版必修四P138.1題改編)銳角△ABC的內角A,B,C的對邊分別為a,b,c,若B=3A,則取值范圍是。
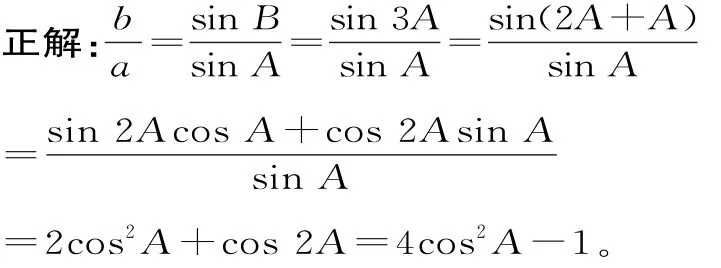
由A+B+C=180°,B=3A,得C=180°-4A。
因為△ABC為銳角三角形,所以A,B,C三個角均為銳角,即同時滿足:
0<A<90°,0<B=3A<90°,0<C=180°-4A<90°。
解得22.5°<A<30°,所以cos30°<cosA<cos22.5°。

所以2<4cos2A-1<1+的取值范圍是(2,1+2)。
警示:這是一道由課本習題改編的耐人回味的新題,能力要求極高:一是需用正弦定理進行邊角互化;二是需用二倍角公式推導三倍角公式(即課本題目);三是需正確詮釋銳角三角形的定義,即三個內角都是銳角求得角A的范圍;四是需用余弦函數單調性及降冪公式求出b的取值范圍。全都是核心主a干知識,哪一個環節不過關,都做不出來。可見,本題是一道源于教材、高于教材,兼具基礎檢測與核心素養考查的好題。
誤區五:各自為政、忽視制約條件致誤
例5 △ABC的內角A,B,C的對邊分別為a,b,c,已知c=+,C=30°,求a+b的最大值。
錯解:因為C=30°,所以B=150°-A。由正弦定理得:

辨析:錯在未弄清A與150°-A之間的關系,本題A與150°-A是相互制約的,不是相互獨立的兩個量,sinA與sin(150°-A)不能同時取得最大值1,因此所得的結果也是錯誤的。
正解:因為C=30°,所以B=150°-A。
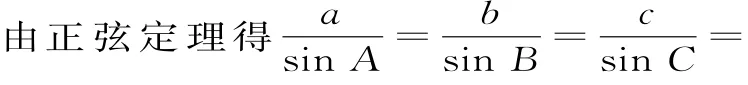

故當且僅當A=75°時,a+b的最大值為8+43。
練習5 在△ABC中,角A,B,C所對的邊為a,b,c已知cosC的值。

誤區六:馬失前蹄、忽視三角形的構成條件致誤
例6 設2a+1,a,2a-1為鈍角三角形的三邊長,求實數a的取值范圍。

易知2a+1為鈍角三角形的最大邊長,設其對角為θ,則90°<θ<180°。

辨析:當a=1時,a+(2a-1)=2,2a+1=3,則a+(2a-1)<2a+1,顯然,此時它們不能構成三角形。“皮之不存,毛將焉附?”連三角形都無法構成,還能構成鈍角三角形嗎?上述解法無疑是錯誤的。錯解錯在忽視了三角形的構成條件,即“三角形任意兩邊之和大于第三邊,任意兩邊之差小于第三邊”,當然有時可變通運用其等價定理:“三角形中,較小的兩邊之和大于最大邊”。
正解:接錯解,注意到三角形三邊的構成條件,得a+(2a-1)>2a+1,解得a>2,故實數a的取值范圍為(2,8)。
警示:解三角形中若涉及邊,要特別注意:“三角形中任意兩邊之和大于第三邊,任意兩邊之差小于第三邊”及“三角形中,大邊對大角、小邊對小角”等性質。
練習6 在△ABC中,如果AB=AC,求函數y=cos A+cos B+cos C的取值范圍。
正解:設內角A,B,C的對邊分別為a,b,c。由AB=AC,得b=c,由余弦定理得:
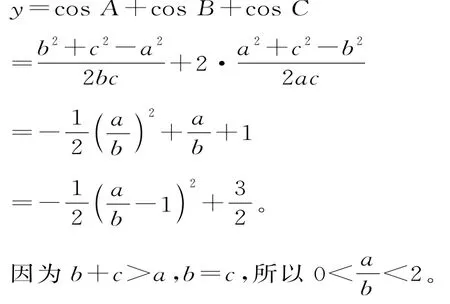
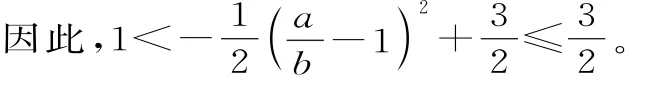
警示:本題若忽視三角形三邊所固有的性質:任意兩邊之和大于第三邊,就會得出函數y=cosA+cosB+cosC的取值范圍為的錯誤答案。
總而言之,解三角形中出現的形形色色的錯誤,其根源在于基礎理論不牢、思維方式不嚴謹。請同學們務必在以下細節上多多用心、避免“陰溝里翻船”。(1)三角形內角和定理;(2)銳角三角形的三個內角都是銳角,鈍角三角形中有一個角是鈍角,其他兩個角必是銳角;(3)三角形中,大邊對大角、小邊對小角;(4)三角形中任意兩邊之和大于第三邊,任意兩邊之差小于第三邊;(5)在△ABC中,a≥b?A≥B?sinA≥sinB?cosA≤cosB;(6)在△ABC中,sin2A=sin2B?2A=2B或2A+2B=π?A=B或A+B=?△ABC為等腰三角形或直角三角形。

