基于可行域調整的多相材料結構拓撲優化設計

俞燎宏，榮見華，唐承鐵，李方義

1.長沙理工大學 汽車與機械工程學院，長沙 410114 2.宜春學院 物理科學與工程技術學院，宜春 336000 3.長沙理工大學 工程車輛安全性設計與可靠性技術湖南省重點實驗室，長沙 410114

結構和材料優化設計已從傳統的單一材料擴展到了多相材料的結構拓撲優化設計。Thomsen[1]較早采用均勻化方法研究了兩相材料拓撲優化問題。Yin和Ananthasuresh[2]將峰值函數引入到SIMP (Solid Isotropic Material with Penalty)方法，并開展了柔性機構多相材料拓撲優化設計。孫士平和張衛紅[3-4]提出了多相材料微結構的多目標優化設計模型，并針對多相材料結構拓撲優化中出現的棋盤格現象，提出了新的周長約束控制方法。Gao和Zhang[5]提出了以質量為約束的多相材料優化模型，并對多相材料的插值模型進行了比較研究。Stegmann和 Lund[6]提出了一種用于復合材料鋪層優化的離散材料優化(Discrete Material Optimization，DMO)方法。在該方法中，將離散的纖維方向特征化為一種材料，DMO插值方案也是SIMP的擴展。而后，Hvejsel和Lund 通過統一參數化將SIMP和RAMP (Rational Approximation of Material Properties)推廣到多相材料結構優化[7]。Blasques等[8-9]利用改進的SIMP多相材料插值模型，開展了復合材料層合梁的多相材料拓撲優化設計。由于在該類基于SIMP的多相材料插值的模型[6-9]中，剛度矩陣明顯存在同一單元的不同設計變量的乘積項，故采用可分離和凸展開的移動漸近線方法(MMA或GCMMA)很難求解含2個以上約束的多相材料拓撲優化問題。最近，DMO拓展到了層壓復合材料的穩健屈曲優化和并發的多尺度優化，并形成了較完善的材料插值模型和求解框架[10-12]。Stegmann和 Lund[6]指出DMO模型的一個困難是優化問題的總體設計空間為非凸空間，并采用僅有2個單元的簡單復合材料單層板設計例子展示了優化問題的多解性、優化解與初始解的關聯性。對于擁有大量變量的多相材料結構拓撲優化問題，采用現有基于SIMP的方法進行多相材料結構拓撲優化求解難于獲得全局優化解[6,12-13]。

Tavakoli和Mohseni[14]提出了交替主動相算法求解多相材料優化問題，先將多相材料優化問題轉化為序列二元相材料優化子問題，然后采用傳統優化準則法進行求解。之后，Tavakoli進一步改進該方法，并求解了彈性動載荷下的復合材料設計問題[15]。Lieu和Lee[16]基于序列二元相拓撲優化子問題求解思路和等幾何分析措施，研究了多相材料多分辨率的結構柔順度拓撲優化設計問題。Park和Sutradhar[17]研究了三維多相材料多分辨率的結構柔順度拓撲優化問題。在上述方法的序列二元相材料優化子問題模型中，僅考慮了一相材料體積約束，且沒有涉及到對不同初始優化拓撲的多樣性設計研究和比較。Zuo和Saitou[18]提出了序列多相材料SIMP插值方法，考慮質量和成本為約束，開展了結構柔順度最小化的多相材料拓撲優化設計。杜義賢等[19]將該模型推廣到了多相材料柔性機構拓撲優化設計問題，然而該模型使得結構性能函數在多相材料懲罰模型曲線的材料變相點處的導數不存在。賈嬌等[20]提出了一種基于多相材料的一體化模型，研究了穩態熱傳導優化設計問題。張憲民等[21]提出一種并行策略，研究了多相材料柔順機構多目標拓撲優化設計問題。龍凱等[22]在結構輕量化設計要求下，提出了基于多相材料的動態拓撲優化方法。另外, 還有水平集方法[23-24]、漸進結構優化方法[25]和相場法[26-27]也用于多相材料的拓撲優化設計。

多相材料連續體拓撲優化是典型的非線性問題，存在大量的局部解[6,28]。從而無法確?；谕挂巹澋奶荻确椒▋灮@得其全局最優解。依據工程實際需求，王博等[28]提出了一種連續體拓撲優化多樣性設計方法。但不同初始拓撲導致優化解差異性的研究文獻較少。如何獲得多相材料拓撲優化設計問題的多個不同的局部解，并最終得到較好的優化解，值得深入研究。本文基于近年來榮見華等提出的可行域調整方法[29-31]，構建與原優化問題等效的多個含2個主動材料相的拓撲優化子問題，改進交替主動相算法，并采用光滑化對偶算法求解。最后，通過算例驗證本文方法的可行性和穩健性, 并說明本文方法解決多相材料結構拓撲優化問題的工程價值。

1 多相材料的結構拓撲優化模型

1.1 多相材料插值模型

參考文獻[29-31]，采用RAMP模型，構建單元體積和單元剛度矩陣的表達式為

(1a)

(1b)

(2)

(3)

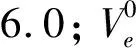
(4)

1.2 多相材料拓撲優化模型及其近似模型

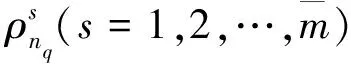
考慮多工況作用，則第l組工況載荷作用下的結構柔順度Cl(ρ)表達式為

l=1,2,…,L

(5)

式中：K(ρ)為結構整體剛度矩陣；Fl為第l組工況載荷；lu為第l組工況載荷作用下所對應的結構位移向量；L為工況數。

借鑒文獻[32]，采用η范數凝聚函數將多個工況的結構柔順度優化問題轉化為一個單目標的優化問題。以結構柔順度最小化為目標、實體材料體積為約束的多相材料拓撲優化模型表示為

(6)

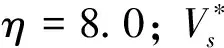
為了增強優化算法的尋優能力和穩健性，參考文獻[31]，引進變體積限可行域調整技術，將優化模型式(6)轉化為近似優化模型，即

(7)

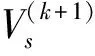
(8a)

(8b)

式中：ρs,(k)為第k外循環迭代步求解獲得的結構中第s相材料的拓撲變量向量；βs為經驗參數，其取值范圍為[0.002, 0.02]。

(9)

(10)

式(9)中，結構柔順度的2階導數采用MMA近似式[33-34]近似獲得。為了處理數值不穩定性問題，采用文獻[25,30]中的靈敏度過濾方法對上述目標函數的1階、2階導數進行過濾。

2 改進的交替主動相算法及求解優化

2.1 改進的交替主動相算法

(11a)

(11b)

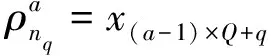
(12)

將優化模型式(7)的求解轉化為式(13)二元相拓撲優化子模型的求解，

(13)

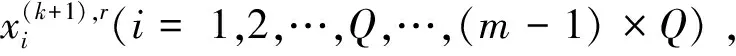
如果a和b兩相材料均為實體材料。根據式(9)，結構柔順度對主動設計變量的1階導數和2階導數可分別表示為

(14)

(15)

根據式(10)，材料體積對主動設計變量的1階導數和2階導數可分別表示為

(16)

(18)

(19)

如果第a相材料為實體材料，第b相材料為空洞材料。根據式(9)，結構柔順度對主動設計變量的1階導數和2階導數分別表示為

(20)

(21)

材料體積對主動設計變量的1階導數和2階導數，可由式(16)和式(17)得到。

因此，二元相拓撲優化子模型式(13)中近似目標函數和材料體積可分別表示為

(22)

(23)

如果第b相材料為空洞相材料，則只有與第a相材料相關的體積約束和其近似函數。

2.2 拓撲優化子模型的求解

參考文獻[29-31]，將人工變量w=[w1w2…wmλ]T引入近似優化子模型式(13)。在y0鄰域范圍內可形成與優化子模型式(13)近似等效的m(m-1)/2個二次規劃優化模型，即

(24)

式中：r+1表示第k+1外循環迭代步兩相材料優化設計迭代的組號；第k+1外循環迭代步的前(m-1)(m-2)/2組兩相材料優化設計時，mλ=2；第k+1外循環迭代步的最后的m-1組兩相材料優化設計時，mλ=1。其中，

(25)

s=a,b

(26)

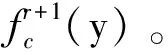
為了減少計算量，采用光滑化對偶方法求解優化模型式(24)，其求解詳細步驟見文獻[29]。

當滿足式(27a)和式(27b)時，優化迭代收斂。

(27a)

(27b)

式中：εs和ε為收斂參數，取εs=ε=0.001。

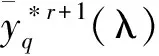
2.3 交替主動相優化設計流程

假設結構由m相材料(含空洞材料)組成，按材料彈性模量值從大到小的順序，依次用數字1, 2, …,m表示材料相。在交替主動相求解過程中，首先，選取第1相和第2相材料，記a=1,b=2，形成二元相拓撲優化子模型，采用光滑化對偶算法求解該子模型，更新設計變量。然后，判斷b=m是否成立，如果不成立，則設置b=b+1，形成新的二元相拓撲優化子模型，求解并更新設計變量；如果b=m成立，則判斷a=m-1是否成立，如果不成立，則設置a=a+1及b=a+1，形成另一個新的二元相拓撲優化子模型，求解并更新設計變量；以此類推。最后，如果a=m-1成立，則判斷優化的收斂性。結構中所有材料按照上述方式兩兩組合，依次求解優化，最后達到多相材料的合理布局。交替主動相優化設計流程圖如圖1所示。

采用文獻[14]中的方法進行優化時，也需按材料彈性模量值從大到小的順序，依次用數字1, 2, …,m表示不同材料相。如果m=3，第1相材料必須設為彈性模量最大的材料，第2相材料設為彈性模量次之的材料，第3相材料設為彈性模量最小的材料。如果調換上述材料相順序，則文獻[14]的程序將無法運行。采用本文方法進行優化時，按照上述主動相方案和材料相順序進行優化設計，獲得的優化結果更佳。如果調換上述材料相順序，獲得的優化結果相對較差。

采用改進的交替主動相方案，將2個材料體積約束與式(8)變體積約束限配合使用，使得該方法適用于不同的初始拓撲變量，增強了該方法對多相材料初始拓撲選擇的靈活性，而且優化過程更為穩健。與單相材料的拓撲優化方法以及沒有兩相主動相材料子模型分解的多相材料優化問題的求解方法相比，該方法只需要增加額外的內循環迭代步。

3 優化算例

3.1 單工況多相材料結構拓撲優化設計

采用文獻[14]中的梁式結構設計算例，用來驗證本文方法的可行性和有效性，并研究本文方法獲得多個局部優化解及尋找較好的優化解的能力。圖2為梁式結構設計域，采用無量綱表示，長度L=96，高度H=48，厚度為1。在結構底邊的點A、點B和點C鉛垂方向分別作用載荷F、2F和F，其中F=1。將圖2所示的結構設計域劃分為96×48個等尺寸四節點平面應力單元。

本算例設置2個優化問題，在優化問題1中，假設結構由兩相實體材料和一相空洞材料組成。第1相和第2相實體材料的彈性模量分別為2.0和1.0，第3相材料(空洞材料)的彈性模量設為1.0×10-9。所有材料的泊松比為0.3。第1相和第2相實體材料目標體積比分別預定為35%和25%。

對于優化問題2，假設結構由三相實體材料和一相空洞材料組成。第1相、第2相和第3相實體材料的彈性模量分別為9.0、3.0和1.0，第4相材料(空洞材料)的彈性模量設為1.0×10-9。所有材料的泊松比為0.3。第1相、第2相和第3相實體材料目標體積比分別預定為20%、10%和10%。

文獻[28]提出了一種連續體拓撲優化多樣性設計方法，在該方法中，將目標函數定義為多個設計構型的目標性能加權之和，加入多樣性度量的約束條件，并形成了基本的優化列式和求解方法?？紤]到多相材料連續體拓撲優化問題的多解性[6,28]，本算例設置了不同的初始拓撲變量，構建多個不同的優化初始拓撲，研究不同初始拓撲對優化結果的影響。采用本文和文獻[14]的方法求解本算例時，過濾長度尺寸rmin=3.0Δmin(Δmin為結構所有單元邊長的最小尺寸)。

由表1可見，基于8個不同的初始多相材料結構拓撲，采用文獻[14]方法程序獲得的8個局部最優多相材料結構構型相似度很大，僅能找出3種有細微差別的局部最優多相材料結構拓撲(見表1中(a)、(b)和(d))，且其結構柔順度大小相差不大。即文獻[14]方法程序分別從8個不同的初始多相材料結構拓撲開始優化設計，最后僅僅得到3種有細微差異的局部最優多相材料結構構型。究其原因，采用基于準則法的傳統拓撲優化求解過程中，設計變量的變化范圍僅由移動限參數move控制[35]。當移動限參數move取小值，比如0.01, 傳統拓撲優化方法[35]可以確保兩外循環迭代步的拓撲變量矢量在一小的鄰域內變化，從而可確保結構柔順度的1階近似式有較好的精度，即傳統準則迭代式所用的結構柔順度導數有較好的精度[35]。然而，當移動限參數move取小值時，基于傳統準則迭代式獲得的優化拓撲往往存在不期望的少量灰度小構件，即該構件的偽密度變量處于0和1之間，很難從最后拓撲中提取滿足約束要求的清晰優化拓撲[35-36]。故Sigmund等建議移動限參數move取較大的值[35-36]，比如0.05或者更大的值。由于一般初始拓撲遠離最優拓撲，當移動限參數move取較大的值時，傳統準則迭代式使得初始迭代的兩外循環迭代步的拓撲變量矢量常不處于一小的鄰域內，其結構柔順度的1階近似式誤差很大，即傳統準則迭代式所用的結構柔順度導數誤差也很大。因此，初始的一些迭代步獲得的解在一定程度上喪失了優化特性。實質上，文獻[14]方法繼承了該特點。盡管文獻[14]方法的程序是一個教育版程序，但它基本反映了文獻[14]方法的特征。

圖3給出了與表1中(a)～(e)相對應的起始幾個外循環迭代步的結構柔順度變化曲線圖。圖4給出了采用相應于表1的不同初始多相材料拓撲和文獻[14]方法求解優化問題1獲得的第8外循環迭代步的多相材料結構拓撲及其柔順度值。

表1采用本文方法和文獻[14]方法求解優化問題1獲得的局部最優結構拓撲及其柔順度值

Table1LocaloptimalstructuraltopologiesandtheircompliancesobtainedbyproposedmethodandmethodinRef.[14]tosolveoptimizationproblem1

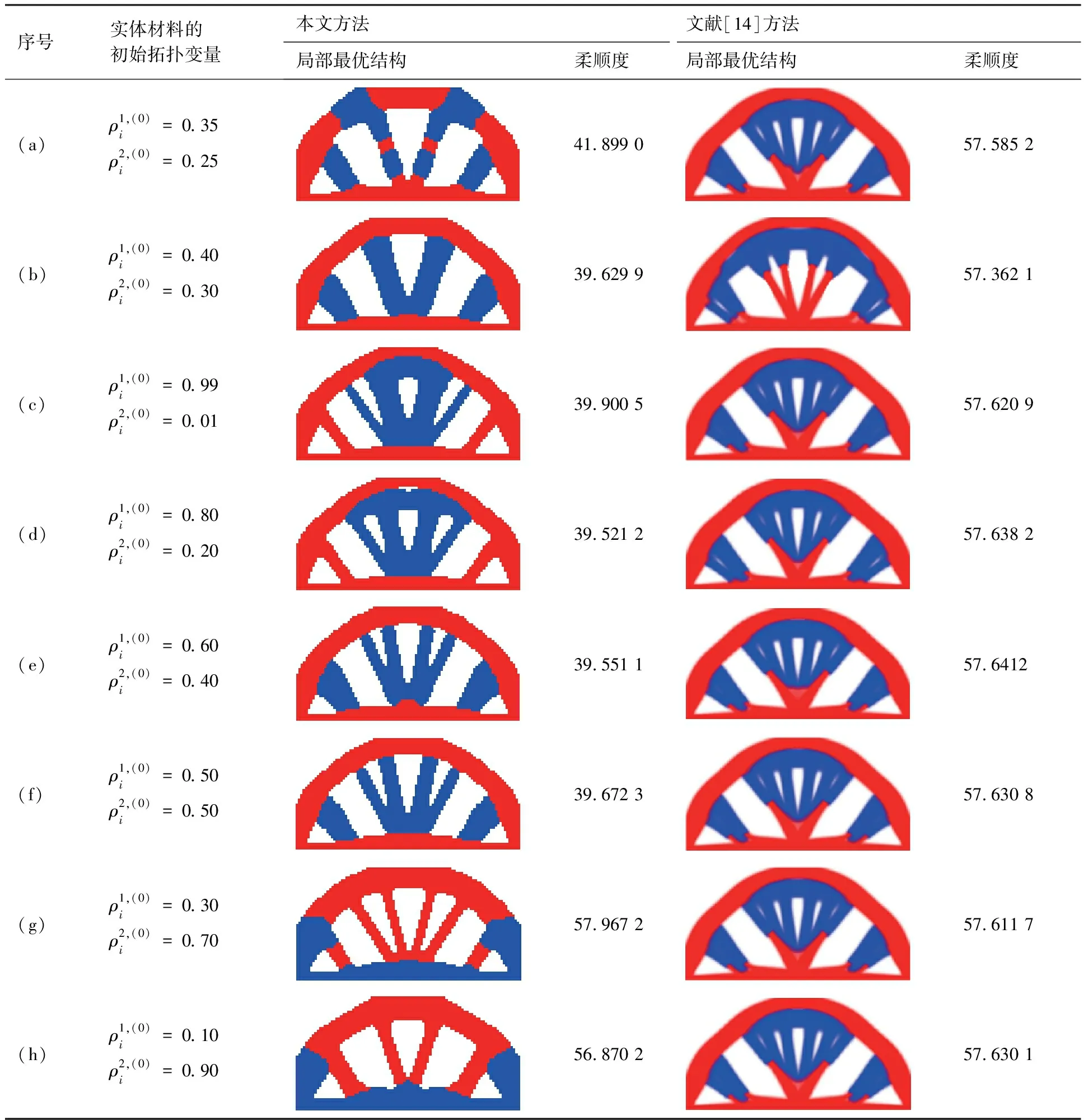
序號實體材料的初始拓撲變量本文方法文獻[14]方法局部最優結構柔順度局部最優結構柔順度(a)ρ1,(0)i=0.35ρ2,(0)i=0.2541.899 057.585 2(b)ρ1,(0)i=0.40ρ2,(0)i=0.3039.629 957.362 1(c)ρ1,(0)i=0.99ρ2,(0)i=0.0139.900 557.620 9(d)ρ1,(0)i=0.80ρ2,(0)i=0.2039.521 257.638 2(e)ρ1,(0)i=0.60ρ2,(0)i=0.4039.551 157.6412(f)ρ1,(0)i=0.50ρ2,(0)i=0.5039.672 357.630 8(g)ρ1,(0)i=0.30ρ2,(0)i=0.7057.967 257.611 7(h)ρ1,(0)i=0.10ρ2,(0)i=0.9056.870 257.630 1

由圖3和圖4可見，初始幾個迭代步的結構柔順度變化很大，多相材料結構拓撲也變化很大，這些都進一步表明文獻[14]方法具有上述特點。從而，多相材料結構拓撲優化特性的部分喪失導致迭代后期的優化解與初始多相材料拓撲的關聯特性的部分喪失。從圖4可知，僅需8個迭代步，原來5個差異較大的初始多相材料拓撲變為5個相似度很大的多相材料結構拓撲。既使后繼的優化迭代比較穩健, 最終獲得的5個局部最優多相材料結構構型的相似度也大。因為多相材料連續體結構拓撲優化問題存在大量的局部解，以及無法確?；谕挂巹澋奶荻确椒▋灮@得其全局最優解。因此，當尋求多相材料連續體拓撲優化問題的較好局部解時，上述特點成為文獻[14]方法的弱點。

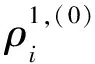
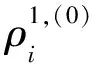
表2給出了結構上下部分的初始拓撲變量取值不同時，采用本文方法求解優化問題1獲得的局部最優結構拓撲及其柔順度值。從表1和表2可見，從不同的初始多相材料拓撲開始優化設計，采用本文方法獲得的局部最優多相材料結構構型基本不同。

表2結構上下部分的初始拓撲變量取值不同時采用本文方法求解優化問題1獲得的局部最優結構拓撲及其柔順度值

Table2Localoptimalstructuraltopologiesandtheircompliancesobtainedbyproposedmethodtosolveoptimizationproblem1whentheupperandlowerpartsofstructurehavedifferentinitialtopologicalvariables

梁式結構設計域實體材料的初始拓撲變量局部最優結構柔順度(a)上半部分初始拓撲變量ρ1,(0)i=0.60, ρ2,(0)i=0.40(b)下半部分初始拓撲變量ρ1,(0)i=0.30, ρ2,(0)i=0.2039.857 9(a)上半部分初始拓撲變量ρ1,(0)i=0.30, ρ2,(0)i=0.20(b)下半部分初始拓撲變量ρ1,(0)i=0.60, ρ2,(0)i=0.4039.893 9

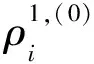
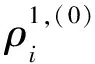
表3采用本文方法和文獻[14]方法求解優化問題2獲得的局部最優結構拓撲及其柔順度值

Table3LocaloptimalstructuraltopologiesandtheircompliancesobtainedbyproposedmethodandmethodinRef.[14]tosolveoptimizationproblem2

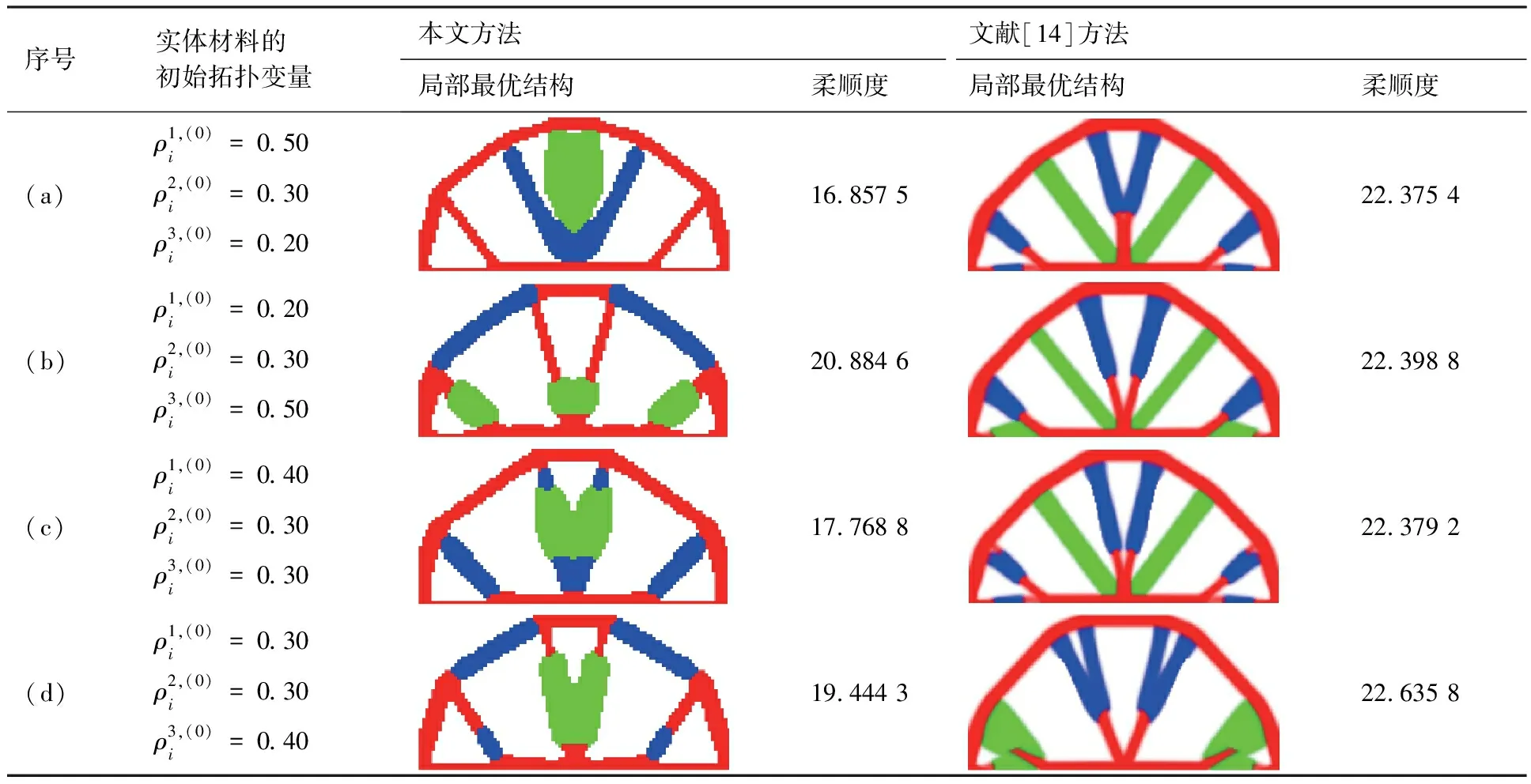
序號實體材料的初始拓撲變量本文方法文獻[14]方法局部最優結構柔順度局部最優結構柔順度(a)ρ1,(0)i=0.50ρ2,(0)i=0.30ρ3,(0)i=0.2016.857 522.375 4(b)ρ1,(0)i=0.20ρ2,(0)i=0.30ρ3,(0)i=0.5020.884 622.398 8(c)ρ1,(0)i=0.40ρ2,(0)i=0.30ρ3,(0)i=0.3017.768 822.379 2(d)ρ1,(0)i=0.30ρ2,(0)i=0.30ρ3,(0)i=0.4019.444 322.635 8

因此，無論是三相或者四相材料結構拓撲優化，本文方法獲得多個局部優化解及尋找較好的優化解的能力比文獻[14]方法強得多。最近，Sanders等[12]提出了一種新的多相材料連續體結構拓撲優化方法, 在該方法中獨立地更新與每一相材料的體積約束相關的拉格朗日乘子，并采用ZPR(Zhang-Paulino-Ramos)設計變量更新方案求解優化問題，實質上該方法是傳統的基于準則的迭代法[35]在多相材料連續體結構拓撲優化中的推廣。在本文方法中，結構柔順度靈敏度計算量是主要的工作量，與現有方法的計算量相同[12]，多個子模型優化求解所需工作量不多，故對三相或者四相材料結構拓撲優化問題來說，本文方法的計算效率與Sanders等[12]方法的計算效率是相近的。對于更多相材料結構拓撲優化問題，本文方法的計算效率略有欠缺。然而，在現有的一些多相材料連續體結構拓撲優化方法中，如果采用自動滿足與式(4)類似要求的多相材料插值方案[9], 則獲得沒有實體材料重疊的優化結構拓撲需很多的外循環迭代步；如果采用不能自動滿足式(4)要求的多相材料插值方案[12]，則需在迭代算法中引入一些啟發式處理措施以確保與式(4)類似的要求和實體材料不重疊的要求[12]，從而降低了獲得的優化解的優化特性。這些情況和上述算例結果表明，本文方法具有更重要的工程應用價值。

3.2 多工況載荷下多相材料結構拓撲優化設計

圖9為矩形結構設計域，長L=3.0 m，高H=1.0 m，厚度為0.01 m。假設第1相實體材料的彈性模量為200 GPa，第2相實體材料的彈性模量為100 GPa，兩相實體材料的泊松比均為0.3。將初始設計域劃分為120×40個等尺寸的平面應力單元，并指定兩相實體材料目標體積比均為20%。

兩工況載荷下結構優化問題(見圖9(a))：矩形結構左右兩側固定，受2個工況載荷作用。工況1：集中載荷F1=10 kN沿鉛垂方向作用在結構下邊中間點A1；工況2：集中載荷F2=10 kN沿鉛垂方向作用在結構上邊中間點A2。

三工況載荷下結構優化問題(見圖9(b))：矩形結構左右兩側中點固定，受3個工況載荷作用。工況1：集中載荷F1=10 kN沿鉛垂方向作用在結構下邊中間點B1；工況2：集中載荷F2=10 kN沿鉛垂方向作用在結構上邊左端點B2；工況3：集中載荷F3=10 kN沿鉛垂方向作用在結構上邊右端點B3。

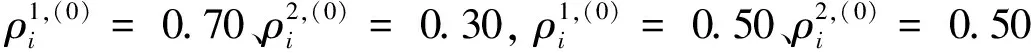
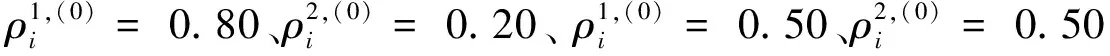
由圖10和圖13可見，采用本文方法也能較好地解決多工況多相材料結構拓撲優化問題，可以找到結構柔順度更小的優化解，再次驗證了本文方法的可行性和有效性。

4 結 論

針對多相材料結構柔順度拓撲優化問題，引進可行域調整技術，改進交替主動相算法，提出了一種新的尋優能力強的拓撲優化設計方法。通過理論推導和數值算例驗證，得出以下結論：

1) 多相材料連續體拓撲優化是典型的非線性問題，存在大量的局部解。從而，無法確保基于凸規劃的梯度方法優化獲得其全局最優解。

2) 設置不同的優化初始拓撲，采用本文方法能夠獲得不同的優化結構，從中可以找到一個更優的多相材料結構拓撲。與文獻[14]方法相比，本文方法具有強的尋找較好優化解的能力。

3) 引入變體積約束限調整技術和改進的交替主動相算法，使得采用本文方法獲得的結構拓撲具有較好的互不重疊的實體材料分布特征。