HTPB黏彈性微裂紋偏折擴展損傷本構模型
顧志旭,鄭堅,彭威,支建莊
陸軍工程大學 火炮工程系,石家莊 050003
端羥基聚丁二烯(HTPB)推進劑是一種廣泛應用于航空航天和軍事武器推進系統的顆粒增強型復合材料,其力學行為直接影響到彈箭武器的使用可靠性[1]。建立準確高效的本構模型,是分析其力學行為的重要前提。
顆粒增強型復合材料的力學行為,不僅取決于組分的性質,更依賴于組分間的細觀結構。當加載應力或應變較小時,材料通常表現出基體的黏彈性特征,而當應力或應變較高時,顆粒/基體界面容易出現“脫濕”損傷而形成微空洞,微空洞生長融合形成微裂紋,微裂紋擴展匯合形成宏觀裂紋,材料又表現出非線性特征[2]。為了描述上述黏彈性損傷行為,許多學者建立了不同的本構模型。一方面,Xu等[3]基于熱力學理論和彈性-黏彈性對應原理建立了熱黏彈性損傷本構模型,該模型能夠預測寬泛溫度范圍下推進劑的本構行為。Yun等[4]引入軟化和循環加載效應函數,建立了可以反映材料Mullins效應的損傷本構模型。此外,還有Park[5]、Ozupek[6]和Jung[7-8]等的一些工作。上述模型主要是從宏觀角度出發,忽略了材料損傷的具體細節,建立的各向同性損傷模型,通常具有較高的計算效率,但模型中往往含有若干物理意義并不十分明確的待定參數,如Xu模型[3]和Park模型[5]中的C(S)線。另一方面,Chen[9-10],Tohgo[11],Xu[12]以及Hur[13]等認為顆粒/基體界面的脫濕是材料損傷的主要機制,利用空洞代替脫濕的顆粒,基于細觀均勻化理論,建立了不同的細觀模型。然而在低應力三軸度時,顆粒/基體界面的脫濕并不完全,顆粒在界面完好的方向仍具有承載能力,上述模型難以反映材料此時表現出的宏觀各向異性特征。從另一個角度,彭威等[14]將界面的脫濕視為微裂紋的擴展,采用微裂紋擴展區的概念,建立了一個能夠表征各向異性損傷的本構模型,但因需要確定多個損傷內變量,并不方便于應用。同時,由于采用了應力強度因子作為微裂紋擴展的判據,該模型不能反映材料的蠕變損傷特征。
由于HTPB材料的高填充比特性(高達85%),脫濕形成的微空洞容易融合而形成微裂紋[15]。因此,本文在一個較大的觀察尺度上,將材料的主要損傷機制視為微裂紋的擴展和匯合,而將顆粒脫濕、微空洞變形等細觀損傷視為裂尖失效區的演化變形。進一步,在Abdel-Tawab宏觀本構方程的基礎上,考慮微裂紋偏折擴展的情形,建立了一個能夠反映材料損傷的應變率和溫度依賴性,以及各向異性損傷特征的黏彈性本構模型。
1 宏觀黏彈性損傷本構方程
Abdel-Tawab和Weltsman[16]基于不可逆熱力學和疊加原理,假定損傷對材料柔量的平衡和瞬態部分具有相同的影響,推導出了如式(1)的本構方程。
(1)
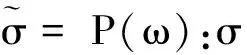
式(1)表明,可以通過有效應力來考慮損傷的影響,但應用的關鍵在于確定損傷映射張量的具體形式。下文基于微裂紋均勻化理論,推導損傷映射張量的一般的形式。
2 損傷映射張量和損傷內變量
定義損傷內變量為
(2)
式中:ai為微裂紋的半徑;ni為裂紋面的單位法向矢量;η為體密度;g(ai)和r(ni)分別為尺寸和取向分布函數;N為微裂紋群數(定義取向和尺寸均相同的微裂紋為一個群);?表示并矢。
根據稀疏估計方法,當忽略摩擦效應時,彈性材料中微裂紋引入的柔度增量可以近似為[17]
ΔSijkl≈
(3)
式中:E0和υ0分別為無損材料的彈性模量和泊松比;ωik為損傷內變量ω的分量;δjl為Kronecker符號。
(4)
式中:S0為無損彈性材料的柔度張量;ΔS(ω)為式(3)定義的柔度增量的張量形式。
根據式(1)中損傷映射張量的定義,有
(5)
將式(3)和式(4)代入式(5),整理得損傷映射張量為
(6)
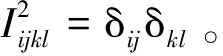
記Stest為實驗測定的柔度張量,Scurrent為微裂紋擴展至當前狀態時的損傷柔度張量,則根據損傷映射張量的定義,有
Stest=S0:Pinitial
(7)
Scurrent=S0:Pcurrent
(8)
式中:Pinitial和Pcurrent分別為初始微裂紋和當前微裂紋狀態對應的損傷映射張量,由式(6)求得。顯然,S0和Scurrent是未知的。在實際應用時,需要找到由Stest向Scurrent映射的損傷映射張量。根據式(7)和式(8),不難得到
(9)
3 黏彈性裂紋擴展演化
3.1 能量擴展準則
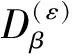
(10)
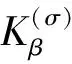
根據式(10),裂紋尖端的張開位移場可以表示為
(11)
式中:ρ為極徑;υ為泊松比。
同時,應力場為
(12)
裂紋擴展長度為Δc時所需能量為
(13)
式中:σγy和uγ分別由式(12)和式(11)給出;s為裂紋擴展長度。
考慮Ⅰ型開裂,令φ=0,將式(11)和式(12)代入式(13),有
(14)
式中:c為裂紋擴展Δc前的尺寸。
裂紋擴展的能量釋放率為
(15)
將式(15)推廣,考慮復合型開裂時,有
(16)
由式(10)和式(16)可見,在蠕變加載下,裂尖的能量釋放率為加載時間的遞增函數。若在加載初期穩定的裂紋(G 假定初始缺陷半徑為a的錢幣形裂紋,則裂尖前緣任一點Q處的應力強度因子為[19] (17) 將式(17)代入式(16),得Q點處的能量釋放率為 GQ(φ)=A1+A2sin2φ+A3cos2φ+A4sin(2φ) (18) 式中: 假定在裂尖法向平面內,裂紋沿周向應力最大的方向進行擴展,則裂紋前緣不同點處的偏折角θk滿足: (19) 式(19)表明,不同點處的偏折角通常并不相同。同樣,A和A′點的偏折角為最大,而B和B′點的偏折角為最小0(發生自相似擴展)。故偏折擴展后的幣形裂紋如圖2所示,裂紋前緣為一橢圓周線,長軸為CC′,短軸為DD′。 對于圖2所示的三維偏折裂紋,分析其對材料柔量的影響時,存在著較大的困難。簡化起見,采用Francois和Dascalu[20]的方法,將其等效為長軸為CC′,短軸為DD′的橢圓形裂紋,并且有 (20) (21) 式中:an和an+1分別為擴展前后的尺寸,如圖3所示;l為偏折擴展的長度,由3.4節擴展速率方程的確定;θkmax為幣形裂紋在A點的偏折角。 為了沿用損傷內變量式(2)的定義,根據Sevostianov和Kachanov[21]的研究,用幣形裂紋來近似上述橢圓形裂紋,兩者的幾何關系為 (22) 式中:L為等效幣形裂紋的半徑;k=f/e,e和f分別為橢圓的長半軸和短半軸;Ξ(k)為第一類完全橢圓積分。 Schapery[22]基于圖4所示的裂紋模型,得到的裂紋擴展速率方程為 (23) 式中:Π為裂紋擴展所需的斷裂能;σm為失效應力;KI為Ⅰ型應力強度因子;C1和n為平面蠕變柔量Cv(t)≈C1tn時對應的系數。圖4所示中,P為真實裂尖,P′為表觀裂尖,α為裂尖失效區長度,d為裂紋張開位移。 假定上一t1時刻,真實裂尖到達H點,表觀裂尖在I點,如圖5所示。當前時刻t,裂紋向前擴展α長度,真實裂尖和表觀裂尖分別到達J和H點。 在Δt=t-t1時間段內,H點的張開位移由0增加到dm[24], (24) 假定KI與t呈冪函數關系,即KI~tμ,并注意到Cv(t)≈C1tn,則有 (25) 式中:r=2μ;κn=Γ(r)Γ(1+n)/Γ(1+n+r)。 裂紋擴展長度為α時所需斷裂能為[24] (26) 將式(26)代入式(23),可得 (27) (28) 式(28)即為裂紋擴展的速率方程。 利用ABAQUS二次開發接口UMAT,將上述模型嵌入其中,進行分析計算。本構方程式(1)的離散方法參見文獻[25],而速率演化方程式(28)采用Euler方法求解,以節省計算量。損傷內變量的計算更新流程如圖6所示。 假定材料初始狀態為各向同性,初始微裂紋空間均勻分布,尺寸為其統計平均值a0。模型參數a0、σm和N對本構曲線的影響,同微裂紋自相似擴展的情形[26],此處不再贅述。 T/℃Gc/(mJ·mm-2)σm/MPaε=5 min-1ε=0.5 min-1ε=0.05 min-1ε=0.005 min-1-400.013.652.321.150.88 200.0010.780.510.420.28 600.000 10.450.370.300.20 表2 臨界能量釋放率Gc的擬合值Table 2 Fitted values of critical energy release rate Gc 不同溫度和應變率下,臨界能量釋放率Gc的擬合值見表2。可見在同一溫度下,Gc受應變率的影響有限,最大變幅為17%。故在表1中將其近似取為常數,并不影響預測結果的準確性,如圖7所示。然而,其受溫度的影響較大,隨著溫度的升高而減小。 為便于說明,定義損傷應力-應變曲線偏離無損曲線的起始點為臨界損傷點(圖7中虛線與實線的交叉點),該點對應的應力為臨界損傷應力,記為σd。不同溫度和應變率下,σd的近似估計值見表3。結合表1可見,失效應力σm取值約為臨界損傷應力σd的1~1.3倍,并且隨著應變率的降低和溫度的升高而減小。這是由于,一方面本文采用了稀疏估計的方法,微裂紋周圍的平均應力就為遠場加載應力。另一方面,受裂尖應力放大效應和脫濕卸載效應的共同影響,裂尖失效區內的平均應力大于微裂紋周圍的平均應力。 表3 臨界損傷應力σd的近似值Table 3 Approximate values of critical damage stress σd 圖8給出了20 ℃,5/min應變率加載下,部分微裂紋的擴展情況。由圖8可見,在單軸x2向加載下,初始θ=90°的微裂紋不發生擴展,而初始θ=7.95°的微裂紋擴展尺寸最大,介于兩者之間的微裂紋,擴展尺寸隨著初始θ角的增大而減小,等效微裂紋向垂直于加載軸的方向偏轉。 (29) (30) 最后,檢驗3.4節中的基本假設KI~tμ。圖10給出了初始θ=7.95°,58.59°的2個微裂紋,分別對應圖1中A和B點的KI-t曲線。其中離散點為UMAT計算的KI值,實線為KI~tμ關系的擬合曲線。由圖10可見,對于不同取向的微裂紋,假設KI~tμ近似成立,但μ的取值并不相同。為便于應用,進一步假定不同微裂紋的μ值相同。當μ取0.5時,式(28)與文獻[24]中的式(76)相同,此時的KI~t0.5擬合曲線如圖9中虛線所示。可見,在一定的誤差范圍內,可以用KI~t0.5來近似KI~tμ,而不影響模型的預測精度,見圖7。 1) 基于黏彈性微裂紋偏折擴展模型建立的損傷本構模型,能夠有效反映材料損傷的應變率和溫度依賴性,以及各向異性損傷特征。 2) 裂尖失效區內的失效應力隨著應變率的降低和溫度升高而減小,取值約為臨界損傷應力的1~1.3倍。臨界能量釋放率隨著溫度的升高而減小,而受應變率的影響較小,同一溫度下可近似為常數。 3) 損傷映射張量具有非完全對稱性,其物理意義是,用等效應力空間中各向同性材料的復雜的多軸加載,模擬真實應力空間中各向異性材料的多軸加載。3.2 裂紋偏折
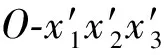
3.3 等效裂紋
3.4 擴展速率方程
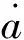
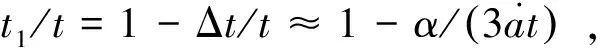
4 模型驗證
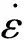
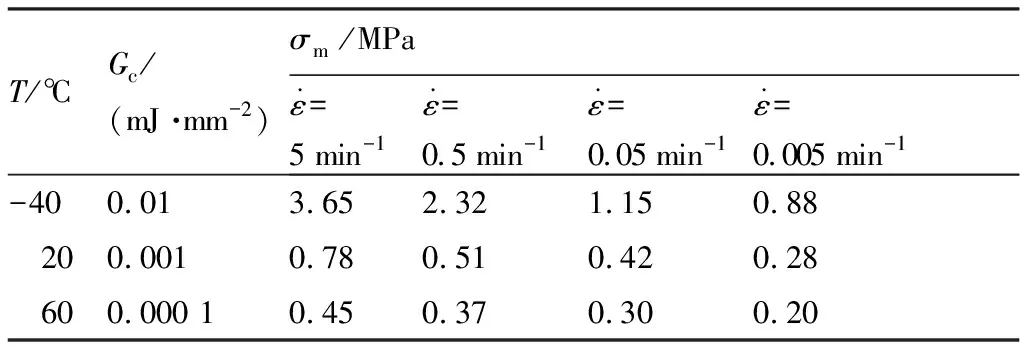

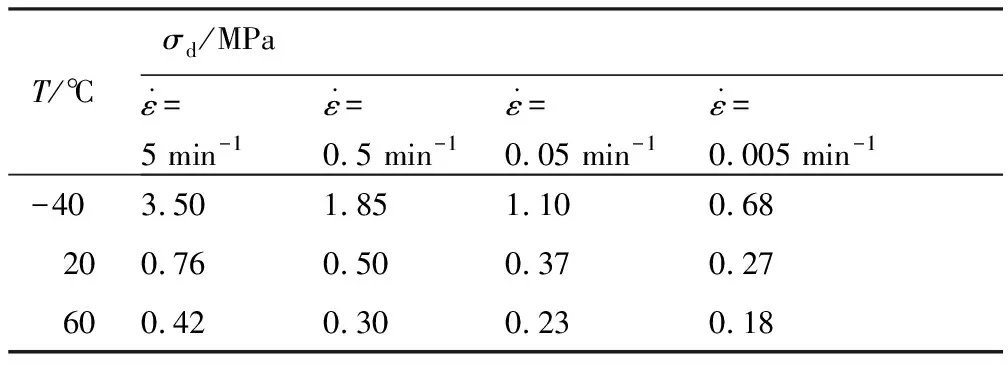
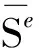
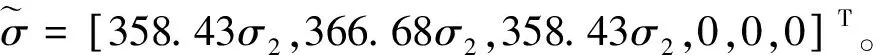
5 結 論

